含有纳米颗粒的悬浮纳米液滴蒸发特性的分子动力学模拟

(1.大连理工大学 化工学院，辽宁 大连 116024 ； 2.大连理工大学 化工机械与安全学院，辽宁 大连 116024)

0 前言

众所周知，含有固体纳米颗粒液滴(即纳米流体液滴)的蒸发(或干燥)特性研究，对于喷雾干燥技术的应用研究至关重要。多年以来，对于宏观尺度含有固体颗粒液滴的蒸发研究，已经取得了很多成果[1-2]。但当含有固体纳米颗粒液滴的尺度达到纳米量级时，其蒸发的实验研究非常困难。随着计算机技术的飞速发展，采用分子动力学模拟方法，来研究含有固体纳米颗粒的纳米液滴的蒸发特性已经成为现实。目前，已有一些研究工作者成功运用分子动力学模拟技术，对纯组分悬浮纳米液滴的蒸发过程进行了探索性研究，但对含有纳米颗粒的悬浮纳米液滴的蒸发过程的分子动力学模拟研究的报道很少[3-6]。本文拟采用分子动力学模拟技术，利用LAMMPS(Large-scale Atomic/Molecular Massively Parallel Simulator)软件，探讨含有固体金属纳米颗粒的悬浮纳米氩液滴的蒸发特性。

1 模拟方法

1.1 模拟体系

模拟体系的初始模型如图1所示。

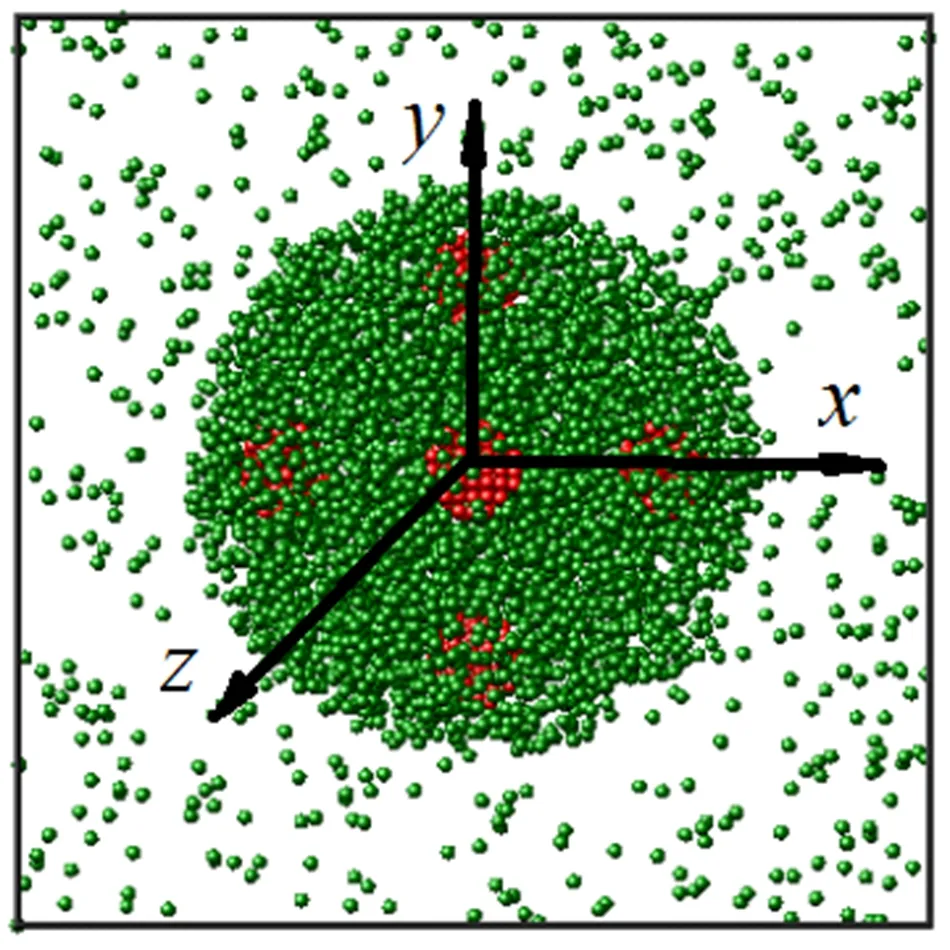
图1 初始模型

采用直角坐标系，球形纳米液滴的球心位于立方体模拟盒子的中心。纳米液滴是由氩流体和纳米金属颗粒组成(即纳米流体液滴)的，纳米液滴内部共有7个固体纳米金属颗粒，1个位于坐标原点，另外6个纳米金属颗粒的球心分别位于x、y和z轴的正负半轴上，纳米金属颗粒中心距离液滴表面一定距离使金属纳米金属颗粒完全沉浸在氩流体中。模拟盒子在x、y、z三个方向上长度为Lx=Ly=Lz=L，初始时刻，一定数量的饱和液体氩原子随机分布成球形纳米液滴，气体空间内根据相应温度下气体饱和密度填充氩原子，氩原子的初始速度是由随机数发生器确定[7]。

1.2 模拟细节

模拟在x、y、z三个方向均采用周期性边界条件，截断半径为1.8 nm。系统采用正则系综(NVT)，采用Woodcock变标度恒温法，实现模拟体系恒温。时间步长取0.5 fs，不断进行质心校正，使质心处于模拟盒子的中心。先经过2 ns使体系达到平衡，再经过5.5 ns进行非平衡分子动力学模拟，计算含有固体金属纳米颗粒的悬浮球形纳米氩液滴的蒸发速率。

1.3 势能函数

在本研究的分子动力学模拟中，对于氩流体原子之间或同种金属原子之间的作用势，采用Lennard-Jones(L-J)势能函数，如方程(1)所示[8]。

(1)

其中：U为势能；rij为分子i和j之间的距离；ε为能量参数；σ为长度参数。如表1所示。

表1 势能参数

对于不同种类的原子之间的作用势，依然采用L-J势能函数，如方程(2)所示[8]。

(2)

其中：rLP为纳米颗粒原子与氩流体分子之间的距离；σLP为纳米颗粒原子与氩流体分子之间的长度参数；εLP为纳米颗粒原子与氩流体分子之间的能量参数。对于不同种类的原子之间的能量参数和长度参数，可由Lorentz-Berthelot混合规则进行计算，如方程(3)和(4)所示[8]。

σLP=(σL+σP)/2

(3)

(4)

其中：σP为纳米颗粒原子之间的长度参数；σL为氩流体分子之间的长度参数；εL为氩流体分子之间的能量参数；εP为纳米颗粒原子之间的能量参数。由于金属原子之间的作用力比较大，因此，在蒸发过程中，这些小的纳米颗粒容易形成一个大的纳米颗粒团聚体。一般认为，在L-J势能函数中，决定原子之间相互吸引力的主要是能量参数。所以，本文将金属原子之间的能量参数缩小为原来的0.3倍，即εP=0.3ε；但长度参数保持不变，即σP=σ。根据表1、方程(3)和方程(4)，计算得到的氩原子与不同金属原子之间的势能参数，如表2所示。

表2 不同原子之间的势能参数

1.4 液相原子数及纳米液滴球形度的确定

Amsterdam规则认为，如果在距离i原子Rij的范围内，至少存在4个j原子，就可以认为，原子i是液相中的原子。其中Rij为原子i和j之间的距离，Rij一般取1.542σ[3]。

对于悬浮纳米液滴的球形度S，其定义如式(5)所示[9]。

(5)

其中：a,b,c分别是球形液滴在坐标轴x、y、z三个方向上的长度，这3个参数可根据LAMMPS软件输出的密度文件得到[9]。

1.5 纳米液滴半径及蒸发速率的确定

假设纳米液滴在蒸发过程中，始终保持规则的球形不变。则纳米液滴的半径R，就可以根据液相原子数，由方程(6)计算得到[9]。

(6)

其中：NL为液相原子数；m为一个液相原子的质量；对于氩，m=6.636×10-26kg；ρL为液相主体密度；R为球形纳米液滴的半径。

蒸发速率是指单位时间内、单位面积上蒸发出来的氩流体分子的质量。本文通过非平衡分子动力学模拟，可以得到液相原子数随时间变化的拟合曲线及其曲线的斜率，再利用方程(7)，就可以得到纳米流体液滴的蒸发速率[9]。

(7)

2 结果与讨论

本文进行的非平衡分子动力学模拟，是通过扩大模拟盒子体积的方法实现的，即模拟盒子的初始边长为12 nm，初始体积为V0，当模拟系统达到平衡后，模拟盒子的6个方向均扩大相同的尺寸，使体积增量达到1.55V0。探讨模拟温度、金属纳米颗粒种类及金属纳米颗粒质量分数对纳米流体液滴球形度和蒸发速率的影响规律。

2.1 温度的影响

在悬浮球形纳米液滴初始直径相同的情况下，加入金属铜纳米颗粒，使液滴中铜纳米颗粒的质量分数达到20%左右。采用非平衡分子动力学模拟方法，计算得到不同温度下的悬浮纳米流体液滴的球形度变化及蒸发速率曲线，分别如图2和图3所示。

图2 不同温度下的悬浮纳米流体液滴的球形度变化曲线

图3 不同温度下的悬浮纳米流体液滴的蒸发速率曲线

由图2可知，随着蒸发时间的增加，含有金属纳米颗粒的纳米液滴的球形度不断变化，总的趋势为逐渐减小。当体系温度较低时，纳米流体液滴的球形度比较大。随着温度的提高，球形度逐渐变小。据此可以认为，模拟温度越高，固体金属纳米颗粒的运动越剧烈，导致纳米流体液滴的球形度越小。由图3可见，当蒸发过程开始时，纳米流体液滴的蒸发速率很大，而且模拟温度越高，蒸发速率越大；之后，伴随着液滴中氩原子的迅速减少，液滴中金属纳米颗粒的质量分数急剧增加，使蒸发速率急剧下降；随着蒸发过程的进一步进行，液滴中氩原子的缓慢减少，液滴中金属铜纳米颗粒的质量分数缓慢增加，使蒸发速率缓慢下降。

2.2 纳米颗粒种类的影响

当悬浮纳米流体液滴中的氩原子数为3 600个，金属纳米颗粒的质量分数约为25%，球形纳米液滴的初始直径相同时，在模拟温度为100 K的条件下，通过非平衡分子动力学模拟方法，得到的金属纳米颗粒种类对悬浮纳米流体液滴球形度及蒸发速率的影响，分别如图4和图5所示，图5 中还与纯组分悬浮球形纳米氩液滴的蒸发速率进行了比较。

图4 金属纳米颗粒种类对悬浮纳米流体液滴球形度的影响

图5 金属纳米颗粒种类对悬浮纳米流体液滴蒸发速率的影响

由图4可知，含有不同金属纳米颗粒液滴的球形度，在蒸发过程中不断变化，其总体趋势为逐渐减小，但都能维持在0.9左右。因此，可以认为，这些液滴在蒸发过程中能够基本保持球形不变。由图5可知，当蒸发过程开始时，与纯组分悬浮球形纳米氩液滴相比，含有不同种金属纳米颗粒的球形纳米液滴，其蒸发速率要小。总体来说，在整个蒸发过程中，这些含有不同金属纳米颗粒的纳米液滴的蒸发速率相差不大，比纯组分的纳米氩液滴要稍小些。由表1和表2中的能量参数可知，金属原子与氩原子之间的作用力要大于氩原子之间的作用力。当含有金属纳米颗粒时，与相同条件的纯组分纳米氩液滴相比，汽-液界面上的原子受到来自液滴内部原子的吸引力会增大，不利于液滴的蒸发。由于这些金属原子与氩原子之间的能量参数相差不大，所以含有不同金属纳米颗粒的液滴蒸发速率相差不大。

2.3 纳米颗粒质量分数的影响

当模拟温度为100 K，悬浮球形纳米液滴的初始直径为8 nm，液滴中铜纳米颗粒的质量分数分别为0、0.077、0.142、0.220和0.295时，采用非平衡分子动力学模拟，计算得到的不同质量分数下的悬浮纳米流体液滴的球形度变化及蒸发速率曲线，分别如图6和图7所示。

图6 纳米颗粒质量分数对悬浮纳米流体液滴球形度的影响

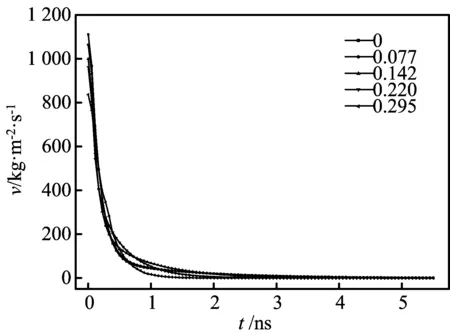
图7 纳米颗粒质量分数对悬浮纳米流体液滴蒸发速率曲线的影响

由图6可知，对于不同质量分数的悬浮球形纳米液滴，在蒸发过程中的球形度不断变化，但总体来说，金属纳米颗粒的质量分数越高，液滴的球形度越小。由图7可见，当蒸发过程开始时，不同质量分数液滴的蒸发速率基本都稍小于纯组分纳米氩液滴的，但相差不大；总体来说，不同质量分数的液滴蒸发速率基本相同。

3 结论

本文采用非平衡分子动力学模拟方法，研究单个含有固体颗粒的悬浮纳米液滴的蒸发特性，得到如下结论：①含有金属纳米颗粒的悬浮球形纳米液滴，在蒸发过程中基本保持球形不变；模拟温度越高，金属纳米颗粒的质量分数越大，纳米流体液滴的球形度越小。②当蒸发过程开始时，纳米流体液滴的蒸发速率很大，而且模拟温度越高，蒸发速率越大；之后，蒸发速率急剧下降；随着蒸发过程的进一步进行，蒸发速率缓慢下降。③金属纳米颗粒的种类和质量分数，对悬浮纳米流体液滴的蒸发速率影响不大。