基于纯几何学线特征匹配的点线结合匹配算法
2020-04-19崔东亮冷建伟
崔东亮 冷建伟
(天津理工大学电气电子工程学院 天津 300384)
0 引 言
当今社会人工智能技术发展愈发迅速,实际应用的过程中对于智能机器人的智能化程度要求愈发提高,同步定位与地图构建SLAM(Simultaneous Location And Mapping)问题开始逐步成为了研究的热点。SLAM问题的目的是如何处理当机器人被置于陌生的环境中时,其怎么通过自身配备的各种的传感器,借由记录计算自身位移数据,以此来实现自主定位以及同步构建增量式地图。在机器人自主移动的领域,SLAM技术有着至关重要的作用。在该系统中,摄像头因为其低廉的成本、便携的体积,并且可以采集到丰富的场景数据而成为主流的传感器。目前主流的SLAM系统利用从收集图像中提取的点特征来进行定位与建图。常用的点特征相关算法有SIFT(Scale Invariant Feature Transform)、SURF(Speed Up Robust Features)、ORB(Oriented FAST and Rotated BRIEF)等成熟跟踪算法。
但是基于点特征构建的地图中,对于某些点特征较少的环境,只依靠点云无法准确地反映场景中的结构信息,点特征与线特征相互对比之下,线特征的维度要比点特征高一个维度,同时线特征在自然环境之中也大量存在,对于一些欠点环境,线特征具有更大的优势,可以更好地还原出场景的信息。文献[1]提出了基于纯几何学的线特征检测算法,对提取出的线特征,通过线段间的几何特征进行匹配,而非传统基于灰度的描述子匹配方法,使得整体算法对于光照变化具有很强鲁棒性,解决了传统算法由于光照的动态变化导致匹配失败的问题,同时由于略去了描述子的计算过程,减少了算法的计算时间。但是算法本身匹配的条件较为严苛,导致算法的匹配数量较少,如果在下一帧中没有检测到对应的匹配特征,会直接的降低算法的整体匹配精度。为了解决这一问题,本文将基于几何学线特征与点特征的匹配算法互相融合。通过融合实时性比较强的ORB算法,增加特征匹配数,构建点线匹配模型,引入Huber核函数进行优化求解,提出一种具有良好实时性与准确性,同时对于光照鲁棒性较强的点线融合算法。
1 点线特征提取与匹配
1.1 点线特征提取算法
特征点的提取和帧与帧之间特征的匹配是点特征相关的视觉里程计的主要组成部分。本文使用ORB[2]与LSD[3]算法作为工具来提取图像中的点线特征。ORB点特征为在图像金字塔中提取的具有方向信息的FAST(feature from accelerated segment test)[4]角点。对于线特征,LSD算法将误差在一定阈值内且梯度方向相似的像素点进行合并,在线性时间里提取图像局部范围内亚像素级的线段作为匹配特征。
1.2 点线融合算法
由上一节可知,图像中的线特征匹配及优化需要花费一定的时间,使得难以保证机器人位置的实时性。为了解决这一问题,本文引入基于点特征的ORB算法。ORB算法在匹配速度上有着明显的优势,能够解决机器人实时定位的问题,但相比于其他速度较慢的基于点特征的匹配算法,ORB算法的累积误差会随着机器人的位移而增大。所以本文综合上述两种匹配算法,提出了一种点线融合的算法,可以在保证算法实时性的前提下,解决系统累积误差过大的问题,同时由于基于纯几何线特征的特性,算法对于那些特征较少、光照变化频繁的场景有着很好的鲁棒性。融合算法示意如图1所示。
1.3 线特征匹配算法
考虑到直线段在连续帧上的几何一致性,即图像中的方向、直线段之间的重叠和极线约束,才能沿着连续视频成功地跟踪直线段,为了给对应直线段增加描述以获得鲁棒匹配,需要引入一些匹配规则来处理与这种纯几何线匹配相关的模糊性。
1.3.1约束条件
为了优化运行时间,增强算法对于光照的鲁棒性,本文采用基于纯几何学的线特征匹配算法。对于连续图像中标记好线特征的两幅图像I1和I2,由直线段的端点坐标s和e将两帧图像的线特征分别定义为L1={si,ei|i∈1,2,…,m},L2={sj,ej|j∈1,2,…,m},由此对于第k条线段,其向量表示为:
(1)
为了描述线特征的有效匹配,将两帧图像中成功匹配的线段定义为M12={(li,lj)|li∈L1,lj∈L2},其中匹配的线特征需要满足平行、长度近似相等、具有足够的重叠部分、符合两个图片的极线约束这些条件。本文通过下式计算线特征之间的夹角来判断是否符合平行条件:
(2)
然而仅通过是否平行进行判断会造成许多错误匹配,因此通过判断线特征是否可以重叠并计算其重叠部分来加以约束。定义ρ∈[0,1]来表示两线特征间的重叠比例,其中ρ=1表示两特征可以完全重叠,ρ=0表示两特征不能重叠。两特线特征之间的长度比例定义如下:
(3)
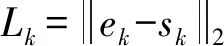
最后考虑两特征的极线约束:
(4)
角度由线特征中点连线向量xij与X轴方向向量决定,其中xij=mi-mj,η1表示X轴方向向量,mk=(sk+ek)/2表示线特征中点。
1.3.2匹配规则
本文通过定义一个n维的向量来代表线特征间的匹配关系:
ωi=[ωi0…ωij…ωin]T
(5)
式中:ωi表示两帧图像中图I1第i条线特征对应的匹配向量,ωi0,ωi2,…,ωin表示图I1第i条线特征与图I2中每一条线特征之间的匹配关系,ω=1表示两线特征满足匹配条件,ω=0表示无法匹配。
根据下式定义线特征间的误差向量βij(图I1中的第i条特征与图I2中的第j条特征间的匹配误差):
(6)
目标向量为:

(7)
通过连接所有误差向量可以得到一个4×n的误差矩阵Ai:
Ai=[βi0…βij…βin]
(8)
算法的目的是找到匹配向量ωi使得匹配误差和可以满足约束Aiωi=b,这样可以保证对于图I1中的线特征i,在图I2中只有一条最佳匹配的线特征与其对应,即问题转化为:
(9)
其约束条件与上述公式对应,其中ε>0。式(9)的解可以利用文献[5]提出的同伦法对下式求解得到:
(10)
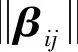
1.4 点特征匹配算法
ORB算法通过计算特征描述子来进行特征匹配,算法首先采用穷举法选择出n对相关系数接近0.5的像素点对,然后根据下式计算二进制特征描述子:

(11)
式中:(x,y)为算法随机选取的像素点对,区块p中p(x)、p(y)表示像素点x、y坐标处的对应的灰度大小,由上述方式可以得到一个n位的二进制特征描述子:
(12)
本文使用K邻近算法[6]进行特征匹配,匹配距离采用Hamming距离。Hamming距离经常在二进制比较中使用,使用异或操作,方法简单,计算速度较快,对比较后的距离给予一个合适的阈值便可以根据需求筛选出正确匹配。
2 位姿估计与优化
2.1 点线观测模型

(13)
2.2 空间线Lw与相机位姿的误差模型

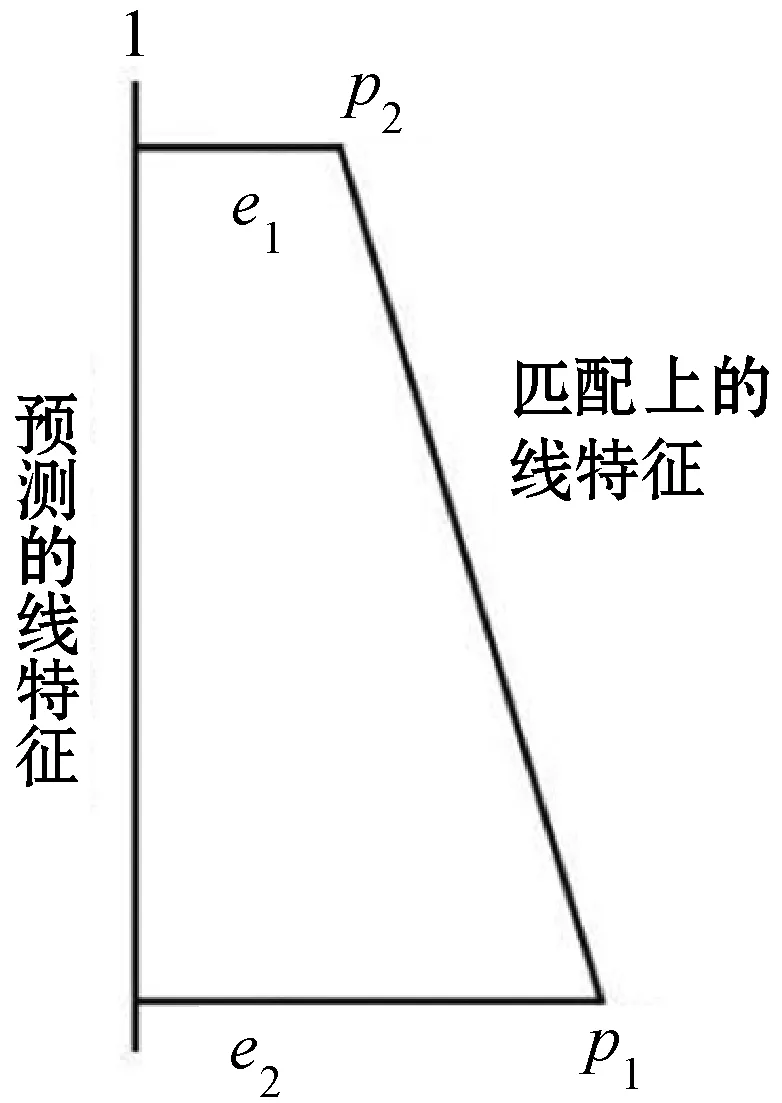
图2 线特征误差示意图
2.3 点线融合误差模型
最后考虑点线融合后的误差模型,根据相机第n帧的位姿Tcw,n与该帧观测到的第m点特征Pw,m的重投影误差和该帧观测到的第q条线特征Lw,q的重投影误差为:
(14)
式中:K表示相机模型的内参矩阵;j表示图像中第j个点或线,d(Luv,n,q,KTcw,nLw,q)表示空间直线与相机位姿的重投影误差。
在对相机位姿进行求解的过程中,将目标函数定义为重投影误差的二范数的平方和。计算过程中错误的匹配对会导致二范数的增速过快,常规算法着重于调整错误误差项的值,存在着忽略其他正确误差项的问题。固本文在目标函数中引入了Huber核函数,以此来减少误差项对优化结果的影响,Huber核函数为:
(15)
由上式可以看出,当误差e大于阈值δ时,目标函数的增长由二次函数变为一次函数,由这种方式来抑制错误匹配对的影响,使得整个优化求解更为稳定。加入Huber核函数的目标函数分别为:
(16)
式中:Ωp和Ωl为点、线的协方差矩阵,Hp和Hl为点、线的Huber鲁棒核函数。通过最小化目标函数的方式来对相机的位姿进行求解:
x*=arg minF(x)
(17)
式中:x*为待优化的变量,即相机的位姿。
2.4 位姿估计
相机的位姿估计问题转化为了求解非线性最小二乘法问题。目前解决这一问题的方法主要有高斯-牛顿法和列文伯格-马尔夸特两种方法。高斯-牛顿法是对目标函数进行一阶泰勒展开,在对结果进行整理后得到增量方程,但是该方法也存在着一定的缺陷,如果求得的增量值Δx过大,会使得算法结果不能够收敛。列文伯格-马尔夸特法在一定程度上修正了这个问题,根据文献[9],本文采用列文伯格-马尔夸特算法对优化问题进行求解。
3 实 验
为了验证融合算法的整体性能,所有实验都运行在Intel核心I5-3370 CPU和4 GB RAM上,没有GPU并行。实验选用Tum数据集来进行性能评估,分别在普通环境下、欠点环境下、光照变化环境下,与LSB+LBD算法、ORB算法进行性能对比。
3.1 数据集预处理
为了验证光照变化对于算法性能的影响,实验前首先对选定数据集进行模拟光照变化处理,分别对部分图像的曝光度、白平衡进行处理,以模拟光照强度变化以及光源变化的影响,数据集前一部分不做任何处理,三分之一处加入模拟光照变化处理,部分数据处理效果如图3所示。

(a) 原始数据集

(b) 模拟曝光变化图3 部分图像预处理
3.2 算法整体性能比较
跟踪效果如图4所示,可以看出在未做模拟光照处理部分三种算法跟踪效果相近,进入模拟光照变化区域后,三种算法对应的轨迹均发生了不同程度的偏移。在desk数据集中(普通环境),融合算法产生的偏移量与其他两种算法相比较小,优于ORB算法,在nostructure数据集中(欠点环境),融合算法表现依然优异,表明融合算法可以很好地适应光照变化的影响。同时通过两组实验对比可以看出在欠点环境下基于线特征的LSD+LBD算法匹配效果要优于ORB算法,这也从侧面反映了点线融合算法在欠点环境下的优势。

(a) desk数据处理对比

(b) nostructure数据处理对比图4 跟踪效果对比图
为了更准确地反映算法性能,表1记录了三种算法在对于不同数据集,普通条件下和模拟光照变换条件下跟踪轨迹与实际轨迹之前的均方根误差。结合表1和图4可以看出,融合算法能够有效地实现轨迹的跟踪,且对光照具有较强的鲁棒性。

表1 融合算法性能评估(普通环境/模拟光照变换环境)
为了验证算法的实时性,实验跟踪记录了帧与帧之间的匹配时间,如图5所示。
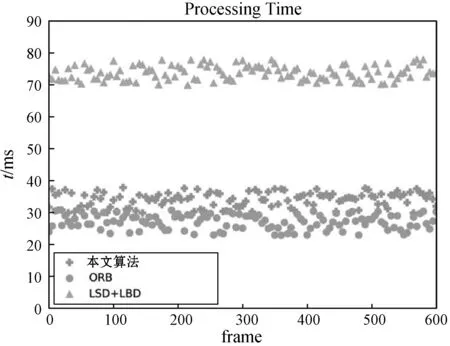
图5 处理时间
LSD+LBD算法平均处理时间为75.32 ms,ORB算法平均处理时间为27.89 ms,融合算法平均处理时间为34.43 ms,对比可知,融合算法虽然稍慢于ORB算法,但足够满足实时性要求。
4 结 语
本文采用改进的纯几何学线特征匹配算法,对光照变化鲁棒性较好、计算速度快,并融合ORB算法以提高特征匹配数量。结合两者优点,改善了传统点特征算法在欠点环境下表现不佳、线特征算法计算量过大等问题,解决了传统算法对于光照变化敏感的问题,同时对融合算法模型进行优化,提高了在系统匹配的准确率。实验表明该算法定位精确度比较高,同时可以满足SLAM系统实时性的需求,但如何进一步提高算法整体效率仍有待研究。
