联合循环平稳特征PCA与XGBoost的频谱感知
2020-04-19束学渊汪立新
束学渊 汪立新
(杭州电子科技大学通信工程学院 浙江 杭州 310018)
0 引 言
随着无线通信技术的快速发展,人们对移动通信的传输速率和时延需求不断提高,各种新技术占用了新的频段,导致频谱资源日趋紧缺。而传统的静态频谱分配方法导致部分频段存在空闲状态的情况,频谱利用率亟待提升[1]。频谱感知作为认知无线电技术的基础与核心技术之一,能够快速准确地对主用户信号进行精确检测,已是人们在研究如何充分利用频谱资源、减少频谱空闲问题的研究热点[2-4]。传统的频谱感知算法主要包括能量检测[5]、匹配滤波器检测[6]和循环平稳特征检测[7]等。传统算法通过构造统计量基于手动调节的阈值进行判决,而人工设定的阈值,受到采样不完全等影响,很难确定较优的阈值,在低信噪比情况下分类效果较差。而基于机器学习的分类算法,在大量数据上通过损失函数进行迭代优化,训练分类模型,模型基于样本特征进行分类判决,避免了用单一阈值进行判决。文献[8-9]将神经网络应用于频谱感知中,在低信噪比下获得了较好的检测概率。文献[10]运用狼群优化方法对训练后的BP神经网络模型的权值矩阵进一步优化,其检测性能优于自组织神经网络算法。文献[11-13]利用支持向量机训练模型对测试信号特征进行分类检测。文献[14]使用随机森林算法作为频谱感知分类器。
本文采用XGBoost算法作为频谱感知分类器。XGBoost算法[15]是陈天奇等于2015提出的一种集成学习算法,是GBDT算法的改进算法。GBDT算法是提升(boosting)方法的一种实现,其思想是不断降低残差,使上一次的迭代模型残差在当前梯度方向上下降,不断优化模型。模型达到较好评估指标一般需要一定数量的CART树,当数据量较大时,会导致GBDT模型计算量巨大,而XGBoost算法在特征粒度上进行并行处理。XGBoost算法在训练之前,预先对数据进行了排序,并以block结构保存,在之后的迭代优化中重复地使用这一结构。在进行节点的分裂时,需要计算每个特征各个切分点的增益,最终选择增益最大的那个特征的切分点去做分裂,对各个特征切分点的增益计算进行并行处理,大大减小了计算量。在迭代优化过程中,GBDT算法的损失函数只进行了一阶泰勒展开,而XGBoost算法对其损失函数进行二阶泰勒展开,对损失函数进行更精确的估计。并且该算法在计算损失时加入正则惩罚项,在迭代优化时进行预剪枝,有效控制模型的复杂度。
1 系统模型
为了对频谱资源展开实时有效的检测,根据认知无线电系统中PU信号频谱感知特点,假设存在W个主用户和G个次级用户,且各主用户信号互不干扰。各路径具有不同时延,并分别进入判决系统中。对任何一个次级用户,可以将其抽象为一个二元假设检验模型:
(1)

2 基于循环平稳信号的特征提取
2.1 信号循环谱特征筛选
假设任意一个二级用户的接收端信号为y(t),其循环自相关函数为:
(2)
式中:α为循环频率;T0为循环周期;R(t,τ)为y(t)的自相关函数。
对其自相关函数进行傅里叶变换得到循环谱密度函数为:

(3)
采用频域平滑法进行循环谱估计,在去除零循环频率情况下,选取能量最大的循环谱向量作为初始样本特征,但是此时数据维度很高,因此采用PCA进行降维处理。
2.2 主成分分析
PCA是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,对高维数据进行降维处理,降低数据冗余。在频谱感知模型中,利用PCA算法对循环谱向量进行降维的主要步骤如下:
设x1,x2,…,xn表示n个在H0或H1情况下信号循环谱能量最大的向量,每个样本向量有m个变量,组成初始数据集矩阵X。
(4)
1) 求矩阵X的相关系数矩阵:
(5)
矩阵R中的元素:
(6)

2) 求矩阵R的特征值,并按从大到小的顺序排列λ1≥λ2≥…≥λm;分别求出对应于特征值的特征向量U1,U2,…,Um。
3) 计算主成分累计贡献率,选取主成分:
(7)
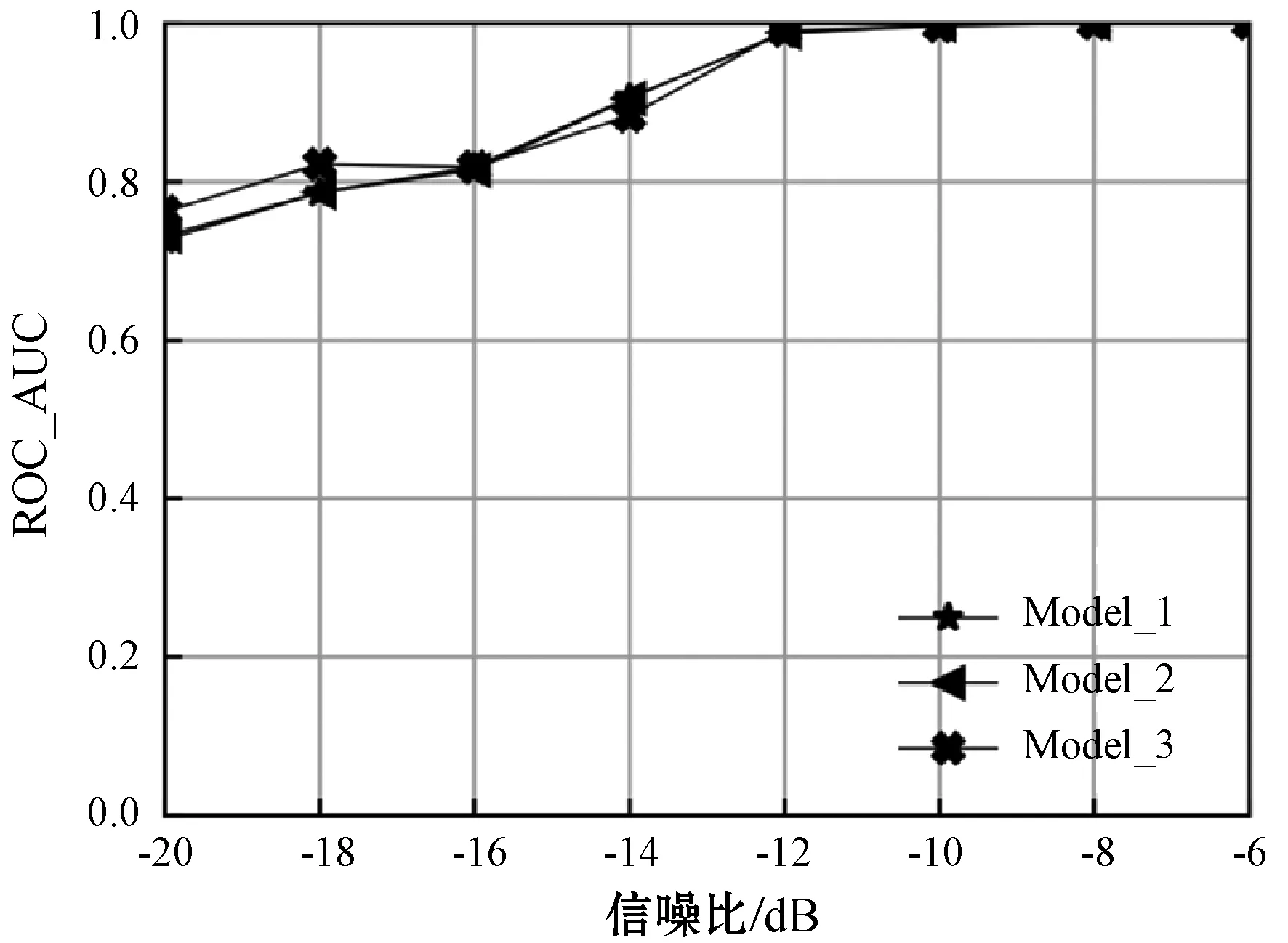
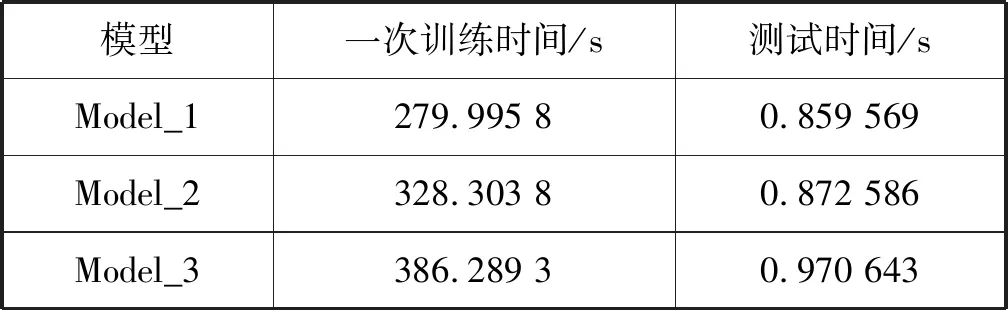
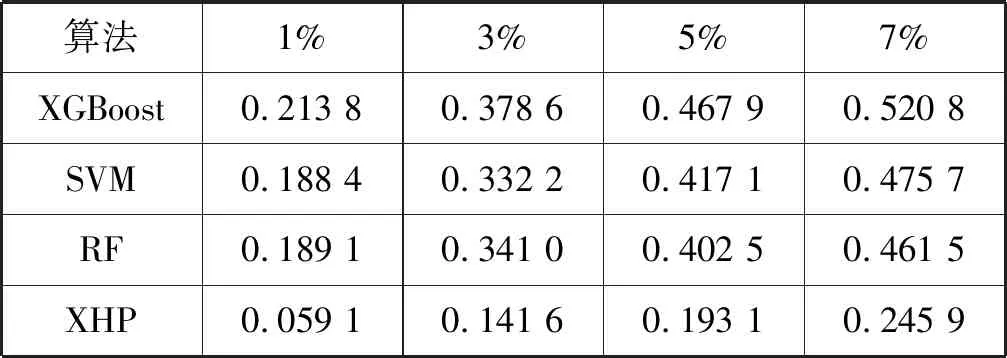
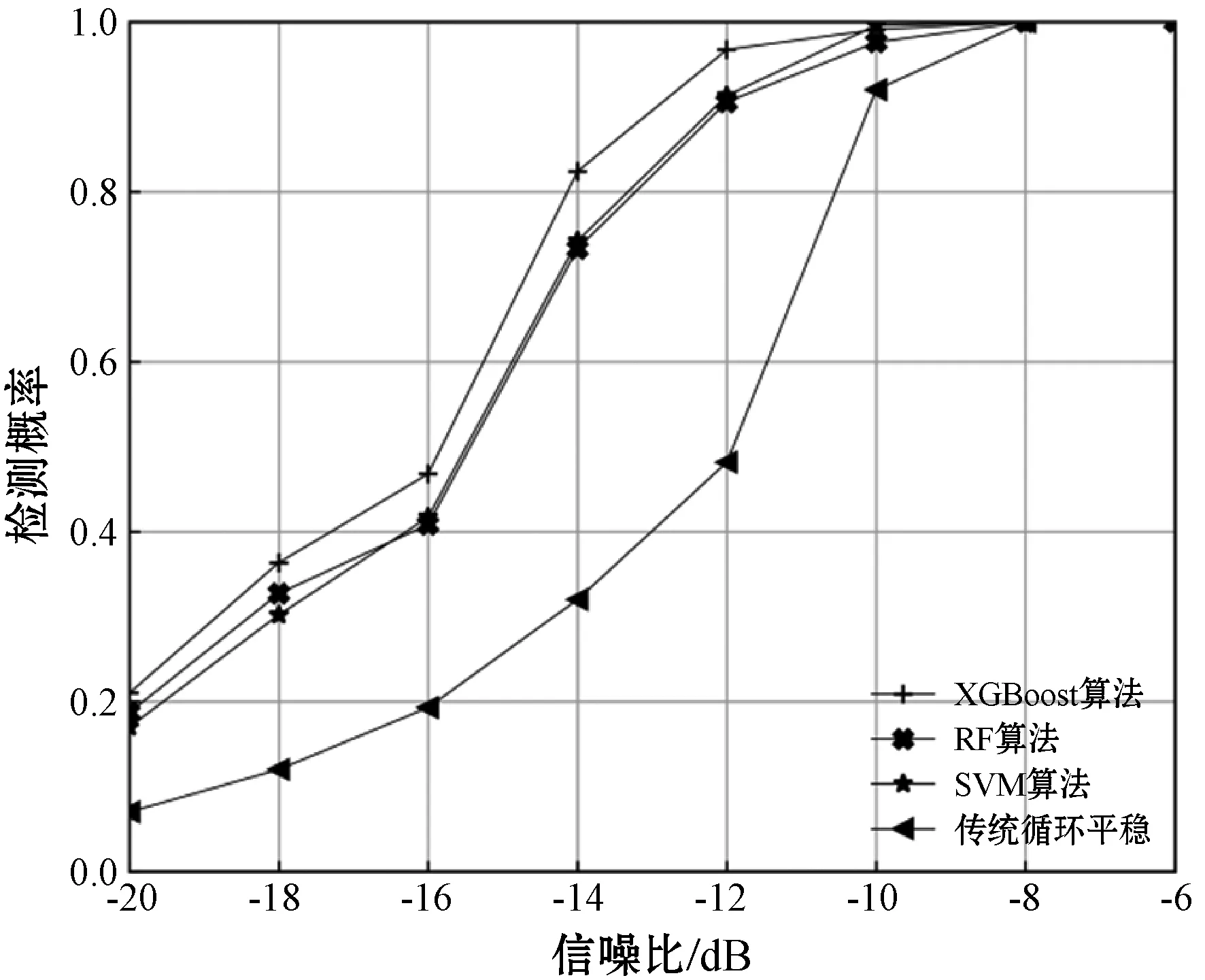
式中:φ(K)累计贡献率;假设threshold≥0.80;K 设Y为降维后取前K个主成分矩阵,则: Y=XU 式中:U=[U1,U2,…,UK]。 通过以上步骤就可以对样本实现降维处理,实现高维数据向低维数据的映射。 XGBoost是串行树结构,第k棵树结构的生成取决于前k-1棵树的结构。XGBoost算法希望建立K个回归树,使得树群的预测值尽可能逼近真实值而且有尽量大的泛化能力,是一个泛函最优化问题。 XGBoost的数学模型表示为: (8) 式中:K为树的棵数;fk(xi)是第k棵树对于输入xi特征的输出得分值;fk是相对应的映射函数;F是相应函数空间。 损失函数表示为: (9) 每次循环的往模型中加入一棵回归树,其损失函数都会发生改变。在加入第t棵树时,前第t-1棵树已经训练完成,此时前t-1棵树的正则惩罚项和训练误差均是已知常数项。 此时,XGBoost的目标函数可以写为: (10) 对于目标损失函数中的正则惩罚项部分,从单一的树结构来考虑,对于其中每一棵回归树,其模型可以写成: ft(x)=wq(x)w∈RT,q:Rd→{1,2,…,T} (11) 式中:T为该树的叶子节点个数;w为叶子节点的得分值;q(x)是模型映射,用来将样本映射到1到T的某个节点内,代表了CART树的结构;wq(x)即为单个树模型对样本x的预测值了。 树的L2复杂度惩罚为: (12) 此时,XGBoost的目标函数可以改写为: (13) 用泰勒二阶展开式近似表示损失函数,将ft(xi)看作Δx,则原目标损失函数可以写成: (14) (15) (16) 式中:T表示第t棵树中叶子节点数量;Ij={i|q(xi)=j}表示分在第j个叶子节点上样本的序号;wj表示第j个叶子节点的打分值。 (17) 对wj求偏导,并令其导函数为0,则有: Gj+(Hj+λ)wj=0 (18) (19) 则目标函数最优值为: (20) L*是用来评估第t棵CART树节点分裂的标准。 评价任意一个特征的任意一个切分点好坏的标准如下: (21) Gain是单节点的L*减去切分后生成的两个节点的L*,Gain如果为正数,并且值越大,就越值得切分。γ是一个临界值,它的值越大,表示对切分后L*降低的幅度要求越严格,相当于在建树的同时做了预剪枝,控制模型的复杂度。 对剩余特征的所有切分点扫描结束后,通过计算确定是否分裂该节点,如果分裂,对分裂出来的两个节点,递归地调用这个分裂过程,最优的树结构找到后,继续迭代生成下一棵树,直到模型达到最优或一定阈值停止。 步骤1根据系统模型,分别在H1和H0情况下,生成信号循环谱。在去除零循环频率后,选取能量最大的循环谱向量作为初始正负样本特征,设正负初始样本分别生成Q1、Q0个。 步骤2利用PCA对初始样本组成的矩阵进行降维变换处理,确定主成分累积贡献率阈值,计算降维后主成份提取维数,获取降维样本数据。 步骤3将样本数据切分为训练样本data_train和测试样本data_test。 步骤4根据上文XGBoost算法生成步骤,利用训练数据data_train对XGBoost算法进行训练优化,通过分步网格搜索确定超参数,确定最终算法模型。 步骤5利用测试样本data_test通过各项指标对算法模型进行评估。 为了验证本文算法在低信噪比条件下的感知效果,以BPSK信号作为主用户信号,在MATLAB R2014a和Python中联合仿真。信号的仿真参数设置为:载波频率fc为3.5 kHz;采样频率fs为500 Hz;采样点数N=4 000。采用频域平滑法进行循环谱估计,通过网格参数搜索确定XGBoost算法的超参数。 实验一训练数据采样对比实验。 本文分别增加低信噪比数据比例和高信噪比数据比例与均匀采样的训练数据作对比,训练数据信噪比取值在-20~-6 dB之间。其中:第一组各信噪比处均为800个;第二组:-10,-12,-14,-16,-18,-20各取800个,-6,-8各取1 200个;第三组:-6,-8,-10,-12,-14,-16各取800个,-18,-20各取1 200个。测试数据各信噪比处均为1 200个。分别将以上三组训练数据使用XGBoost算法训练出三个模型model_1、model_2、model_3,各模型测试结果如图1、表1所示。 图1 模型在各信噪比测试数据上AUC值 表1 三组模型时间效率对比 从图1可以看出,Model_2表现相对于Model_1基本一致,由于低信噪比处数据噪声较少,模型对低噪声数据分类效果已经接近极限,增加数据量也不会提升其表现,只会增加模型训练和测试时间。Model_3相对于Model_1在-18 dB、-20 dB处的测试集AUC值分别提升4.57%、4.97%,在-14 dB处下降2.54%,这表明增加低信噪比数据可使得模型在低信噪处表现有一定提升,但是其一次训练时间相对于Model_1增加了37.96%,通过网格搜索或分步网格搜索其训练时间增加量是很大的。此外对一共9 600个测试样本来看,Model_3的检测效率明显降低,相对于Model_1其检测时间增加了12.92%,这表明Model_3的复杂度更高。因此以下实验均采用第一组训练数据采集方案。 实验二信号检测性能对比实验。 图2为在信噪比分别为-12 dB、-16 dB情况下基于XGBoost、RF、SVM的循环平稳特征算法与传统循环平稳特征算法ROC曲线的比较,可以看出基于机器学习的改进算法在各虚警率处均明显高与传统算法。而基于XGBoost的改进算法在各信噪比的检测概率均优于基于SVM和RF的改进算法。如表2所示,在虚警率为0.01、0.03、0.05、0.07处,测试数据-12 dB时,XGBoost改进算法的检测概率相对于SVM改进算法分别提升8.53%、5.34%、5.92%、5.17%,相对于RF改进算法分别提升7.62%、7.31%、6.81%、3.62%。如表3所示,测试数据为-16 dB时,XGBoost改进算法的检测概率相对于SVM改进算法分别提升13.48%、13.95%、12.18%、9.48%,相对于RF改进算法分别提升13.11%、11.03%、16.25%、12.84%。这说明XGBoost改进算法在低虚警率情况下提升明显。 图2 基于XGBoost算法和RF算法、SVM算法、 传统循环平稳特征算法ROC曲线比较 表2 SNR为-12 dB,各算法在低虚警率处检测概率比较 表3 SNR为-16 dB,各算法在低虚警率处检测概率比较 实验三信号检测概率对比实验。 图3为在虚警率为0.05的情况下,当信噪比大于等于-8 dB时,各算法均达到或接近100%的检测概率。在信噪比小于等于-10 dB时,基于机器学习的改进算法大幅优于传统的循环。XGBoost算法在低信噪比时也全面优于SVM算法和RF算法,在信噪比为-14 dB、-16 dB、-18 dB、-20 dB时,XGBoost算法相对于SVM算法分别提升了11.05%、12.21%、20.36%、23.53%,相对于RF算法分别提升了12.42%、14.54%、11.13%、12.24%。这说明XGBoost算法有更好的抗噪声能力。 图3 三种算法在不同信噪比下检测概率比较 本文提出了一种基于极限梯度提升树的循环谱特征频谱感知算法,通过对比支持向量算法、随机森林算法、传统循环平稳特征算法,本文算法在低信噪比处检测概率明显优于传统机器学习算法和传统循环谱算法。后续将尝试构造新特征,并做模型融合尝试。3 XGBoost算法
3.1 损失函数

3.2 求解节点最优值
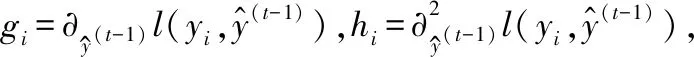



3.3 求解最优树结构

4 频谱感知算法步骤
5 实验与分析


6 结 语
