基于T-prim模型的肺气管分割算法
2020-04-19石跃祥
石跃祥 杜 祎
(湘潭大学 湖南 湘潭 411105)
0 引 言
肺部疾病已成为世界范围内人类发病率和死亡率提升的主要原因之一,其影响预计将在未来20年内增加,届时它将成为第三大死亡原因和第五大发病原因[1]。而针对肺部疾病的治疗必须基于科学高效的现代医学技术,只有这样患者才可以从治疗中获益。医学图像解释和决策被认为是诊断放射学中最重要的过程[3]。为了帮助放射科医生进行图像解释,医学图像的计算机分析最近已在临床上实施,分割出肺气管树的形态可以作为指导医生针对病理过程进行治疗观察的标签[5],从而针对病灶不同阶段的过渡治疗与检测会变得更加准确而高效。而图像分割是研究人员面临的经典难题之一。
随着医学影像学的发展,图像分割在医学应用中起着重要的作用。为了取得这些研究的成果,精确地分割出肺气管树是不可缺少的。然而,对位于肺气管树末端更细小、更高级的气管进行分割是很困难的。Thorsten等[2]提出的同步肺气管分割和重建方法在分割阶段执行了骨架算法,从而有助于防止在快速行进生长过程漏入肺实质。数学形态学方法使用一系列的形态学结构元素进行分割[6]。Francoise等[4]结合形态滤波、连接样本标记和条件分水岭算法对支气管进行分割。有一种基于增强管状结构的肺气管树识别策略表现更为优异。Aykac等[7]首先利用核尺寸增大的形态闭合操作进行二维灰度气道重建,然后采用迭代闭合和扩张操作获得所有潜在肺气管,最后采用前后连通的三维形态重建抑制噪声,分割出完整的肺气管树。Saba等[8]使用肺气管树的三维模型和扫描仪的点扩散函数进行了二维测量,与半波宽(FWHM)算法[9]相比,获得了更好的内边界亚像素精度,在针对外气管壁边界的比较实验中也取得了更好的效果[11]。Preteux等[10]使用多项式估算肺气管内壁位置,但会使细支气管的分割误差大大增加。Kerschnitzki等[11]根据输入图像与气管和气管壁两个标志物之间强度的相似性,为每个体素分配一个模糊成员。该算法允许两个区域相互竞争,从而决定了所有体素的类标签。模糊连通性也可用于肺血管分割。Naqibullah等[15]提出了一种基于形态学的人工肺气管树分割方案,该方案基于模糊连通性(FC)方法来抑制进入周围区域泄漏。这些方法在分割过程中保留了支气管分支的圆柱形特征,在六代支气管之内能够检测到更多的分支。虽然这一过程可以进一步帮助识别细小支气管的位置,但也会在肺部区域产生难以避免的假阳性现象。Charbonnier等[13]采用深度学习法的方法分割肺气管,使用深度神经网络提取特征值,用于查找泄漏并通过调整网络参数以消除分割过程中的泄漏,但计算成本非常高。
由于肺气管结构固有的复杂性以及CT图像分辨率的局限性,大多数肺气管分割方法对主气管和一些明显的支气管的分割是有效的[9]。这些算法通常依赖于CT上气道的外观(二维的暗椭圆形状等),或者基于一些预先定义的基于解剖的规则来控制分割过程。然而,这些规则和假设在噪声、人工干预,或气管病变的存在下可能是不准确的。对于高阶的细小支气管,迫切需要一种分割方法来精确地分割出肺气管树。
本文的创新点在于:(1) 对分水岭算法分割框架进行了优化,并在马尔可夫随机场的角度对优化分割框架进行了进一步的修改,可用于从多个对象背景分割出特定的类。(2) 对prim最小生成树算法进行改进,提出一种T-prim模型。根据以上优化框架得到的最优能量函数构建了评价支气管灰度数据的可信度评价标准,以此结果作为阈值执行MST算法获得完整的肺气管树结构。通过与EXACT09竞赛算法的效果作对比验证了本文算法能够快速准确地分割出完整的肺部气管树,在整个过程中几乎不会出现泄露误分割等现象。
1 马尔可夫场角度下的分水岭算法分割框架优化
1.1 分水岭算法的优化分割框架
文献[14]提供了一个通用的分割方案,该框架可以提供利用种子节点进行分割的算法,可以对该框架进行进一步扩展。本文取其中分水岭最小生成树算法作为一个特殊的案例进行优化使用。通过将该算法应用于肺气管树分割环境,对该类分水岭分割模型进行了具体化改进。
将无向图定义为Go=(Vo,Eo),带有节点集Vo以及边界集Eo,其中Eo⊆Vo×Vo,基数n=|Vo|,m=|Eo|。vi和eij分别代表Vo、Eo中的节点和边界。由图像灰度生成权重值,对wij做如下设置:
wij=exp(-β(▽I)2)
(1)
式中:▽I为图像I的归一化梯度,灰度图像的梯度为Ii-Ij,假设权重为非负,wij为边界eij的权重。广义能量由下式给出:
(2)
式中:y表示测量配置,x表示目标配置;wij为目标配置梯度的权重。
假设G为一个无向图,则wij=wji。该两类分割图优化方法框架为:
Step1
(3)
s.t.x(F)=1,x(B)=0
Step2
(4)
式中:xi、si分别代表节点vi的背景概率以及结果标签。x是Vo中所有节点的概率集合。至此将框架扩展到分水岭算法领域。
1.2 马尔可夫随机场角度的能量最小化框架

p(si=1|xi)=max{min{xi,1},0}=
(5)
若辅助节点的值介于0和1之间,则当权重均为正值时,取其值介于0和1之间。因此可以使用p(si=1|xi)=xi,不必担心xi在[0,1]之外。
在图像数据I中推断隐含变量xi。通过后验模型,可以在贝叶斯框架中估计出隐含变量。
p(x,s|I)∝p(x)p(s|x)p(I/s)=
(6)
模型p(x)中,伯努利变量的参数在空间上不断变化。平滑处理后,空间先验概率参数初始化为:
(7)
式中:λ>0,权值为正值。可以估算出边缘化映射准则:

(8)
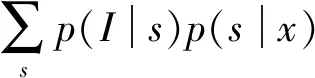
(9)
式中:wi0≥0,wi1≥0,可将参数xi纠正到0和1之间。通过设置种子节点vi的权重(wi0,wi1)=(0,∞),背景节点权重(wi0,wi1)=(∞,0)。参数化之后,图像估计值可转化为求式(5)中能量函数最小化问题。详细过程为:
p(x,y|I)∝p(y|x,I)p(x|I)=p(y|x)p(x|I)=
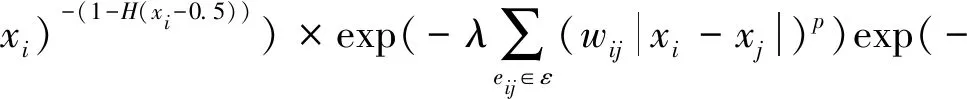
(10)

(11)

(12)
如果p=∞,集合ε包含模型(11),通过p范数使E(x)参数化:
(13)
2 T-prim模型
2.1 模型构建
T-prim模型的构建方式与经典的prim最小生成树的节点生成方式相似。其中一个主要的改进是prim算法需要到达图中的所有节点,但在本文算法中,如果堆栈中没有符合权值条件(Ts≥τ)的对象节点,则这些节点不会被纳入最小生成树。而且,prim树的生成可以看作是一阶马尔可夫过程,用于以最小边缘添加节点来构建树的结构。因此T-prim模型可使用在上一节的优化分割框架中。在该算法中,执行的目标是在树中添加具有最大加权和管状结构分数(Ts)的节点。如图1所示。

图1 T-prim构造图
图1中,vi∈VT-prim。vp是用于实现的虚拟图形节点。e(vp,VT-prim)表示所有边缘集,包括连接节点vp和VT-prim中的节点的所有边缘。这些边缘用图中的虚线表示。e(vp,Svy)代表所有连接vp和肺气管种子节点的边缘。最终构造的图形包括两部分:图像网格(Go)和T-prim部分(G′)(虚线和关联节点)。
当确定一个种子节点之后,凭借与管状结构权值的极大值评分(Ts)来迭代添加节点,直到T-prim被构建起来。在实际应用中,树形结构会非常稠密,尤其是在细小的支气管区域中。根节点和气管以外节点的路径上可能存在许多节点。管状结构评分(Ts)的计算是非常重要的部分。Ts计算方式如下:
Ts(vi)=λ×Ts(vi-1)+(1-λ)×mf(vi,di)=
(14)
式中:di=vi-vi-1。当i=1时,则:
(15)

(16)
(17)

2.2 优化分割框架的使用
与二维图像相比,三维图像的分割任务显得更加重要和困难。对于肺气管树分割,由上一节可知,优化框架可以修改为以下目标函数:
(18)
s.t.x(SV)=1,x(SB)=0
最小生成树模型T-prim=(ET-prim,VT-prim)中包含边界集合ET-prim和节点集合VT-prim。Twi为节点vi∈VT-prim的T-prim管状结构响应。SV和SB代表肺气管种子集合和背景区域种子集合。在这个目标函数中,所做改动删除了前景和背景的原始区域能量项,并为集合中的节点添加了一个新的集合VT-prim,来衡量肺气管数据的可信度。

(19)
s.t.x(SV)=1,x(SB)=0
这样对该目标函数使用上一节优化的功率分水岭框架构造出图结构,完成分割。总体过程梳理为下:
输入为图像数据像素集I,肺气管种子节点SV,背景区域节点SB。在图像I中,Eo为连接相邻像素边缘的集合,Vo为肺气管壁的像素集合。计算权值的参数为w,定义Go=(Vo,Eo)计算权值wo={wij=exp(-(Ii-Ij)2/(2w2))}。得到maxw=max{wij∈wo}。执行上一节所述过程,利用I、SV以及maxw获得T-prim和Tw。由定义可知G′=(V′,E′),其中V′=vp∪Vtp∪Svy,E′=e(vp,Sv)∪e(vp,Vtp)。则:
W′(e(vp,Sv))=maxw
(20)
W′(e(vp,Vtp))=Tw(Vtp)
(21)
令G=Go∪G′,W=Wo∪W′,将G输入上一节马尔可夫随机场角度优化的分水岭分割框架,得到X,即为输出。
2.3 总体分割过程
本文采用三维混合方法完成肺气管树的分割。包括三维形态重建、T-prim模型和区域生长,优化的分水岭算法框架。
首先通过三维形态重建和区域生长算法的灵活运用,获得肺主气管。之后改进prim算法构造T-prim模型,T-prim模型提供了良好的数据可信度权值,并进行了初步的图形构建。然后利用优化的分水岭分割算法通过分割目标函数的能量函数优化结果构造了完整的图,最大程度避免渗漏,从而获得细支气管。这里的关键思想是,不仅基于单个体素的像素,而且基于来自周围环境的信息来决定区域的增长。
具体地说,在主气管骨架提取的基础上,可以自动获取T-prim的初始种子点,然后通过其算法的迭代过程生成T-prim中的节点。当T-prim建模在肺叶支气管中完成,利用优化分割框架细支气管可以有效地分割出来,并且极少出现泄露问题。分割框架如图2所示。
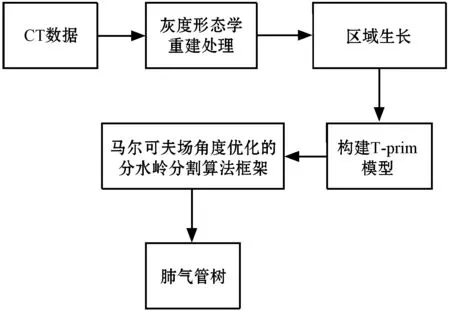
图2 分割框架
至此完成算法分割过程。本文算法的创新主要在于:在肺气管分割领域对prim最小生成树算法进行改进,引入构建T-prim模型。对原有的分水岭分割框架从马尔可夫链角度进行扩展优化,使其适用于T-prim模型构造,利用T-prim构造新目标函数,对新的能量函数进行优化完成对细支气管的分割。
3 实验与分析
为了验证本算法的有效性,这里给出了本文算法在EXACT09竞赛后20例测试数据中的分割结果,并用其标准进行评估,这是国际公认的肺气管分割参考标准。
3.1 肺气管分割结果展示
本实验结果均在VS2015与MITK平台上得到。竞赛中的40例数据中,前20例数据供参赛算法用来进行实验或作为训练集。后20例数据集用作算法的测试。这些测试数据包含一套完全独立的异质性扫描,包括不同重建核的吸气和呼气扫描,以及不同程度的间质性肺病[12]。使用这一个公共数据集可以直接比较不同方法。图3为本文算法的分割结果。
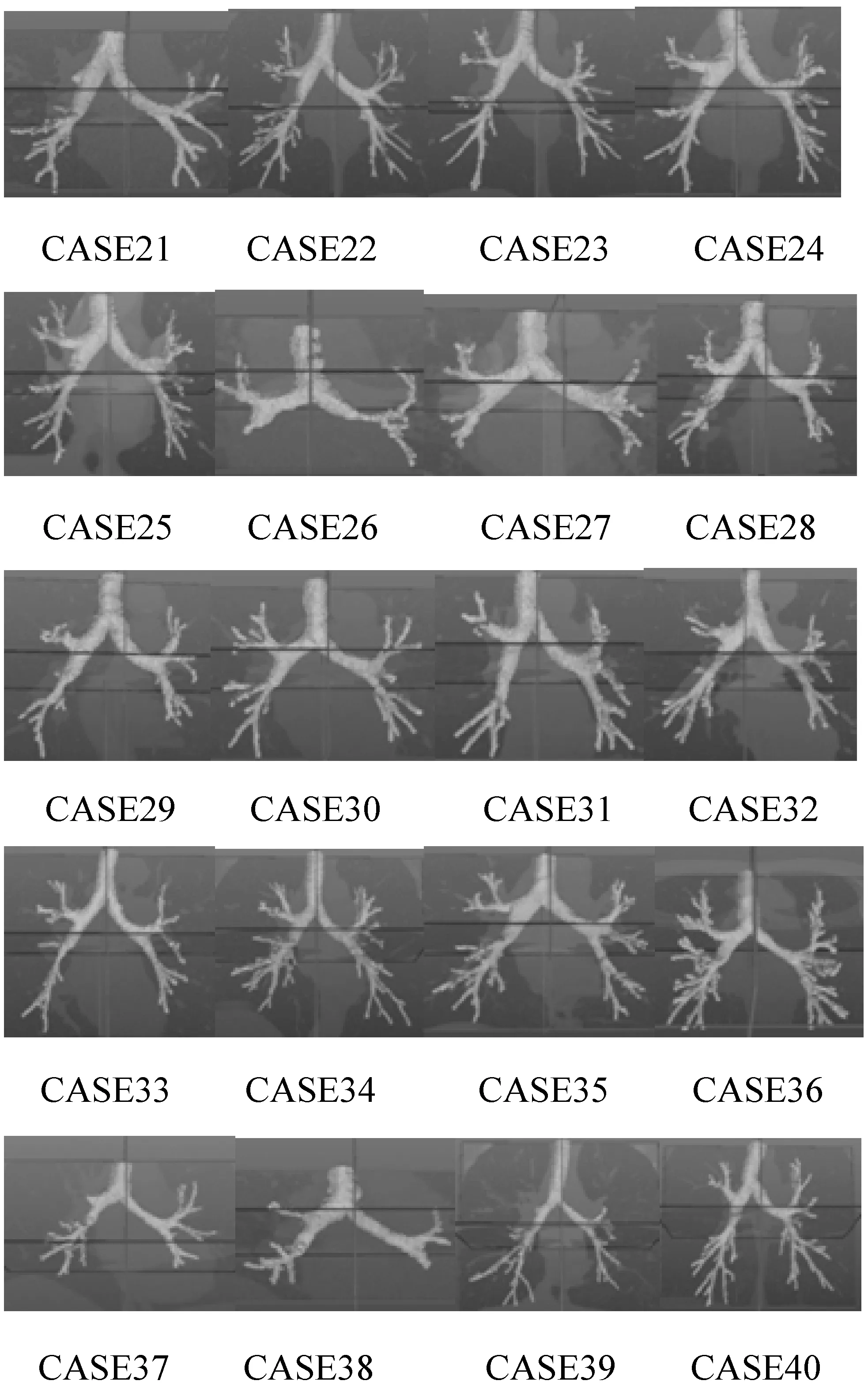
图3 三维重建算法分割结果展示
3.2 与两种EXACT09算法的对比实验

将本文算法与EXACT09竞赛中Weinherimer等以及Wiemker等提出的算法进行对比。两者算法均有采用过基于图形构造的方法,与本文算法有一定的可比性,存在一定的竞争对比关系。对比结果如图4-图6所示。

(a) 与Weinherimer等分割结果对比
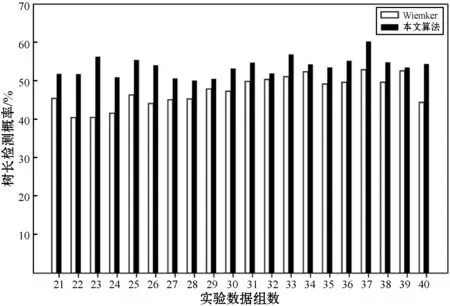
(b) 与Wiemker等分割结果对比图4 正确检测树长与检测树总长比值对比图

(a) 与Weinherimer等分割结果对比

(b) 与Wiemker等分割结果对比图5 假阳性对比图

(a) 与Weinherimer等分割结果对比
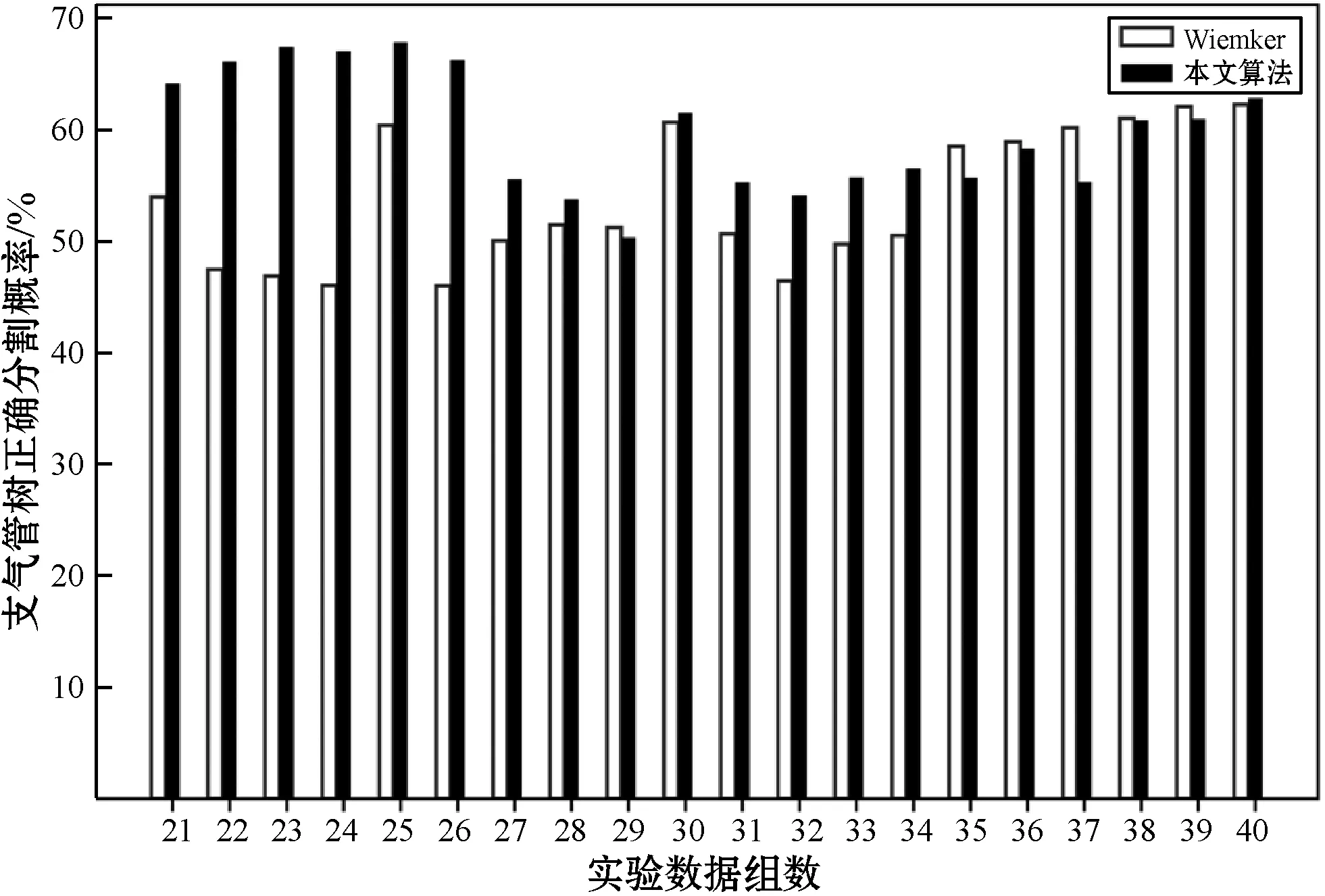
(b) 与Wiemker等分割结果对比图6 正测到的分支数与总支气管分支数比值对比图
可以看出,本文算法分割的树长,正确检测到的支气管树基本上好于其他两者,而且本文算法明显具有更优秀的防泄漏性能。
3.3 与在EXACT09算法中的性能评测
图7为本文算法与EXACT09竞赛15种算法平均值的对比结果,其中:(a)为针对后20例测试数据所分割出正确分支的数目;(b)为针对后20例数据分割结果种泄露或错误的体积。本文算法在泄露极少的情况下达到了EXACT09竞赛算法的平均水平线之上。
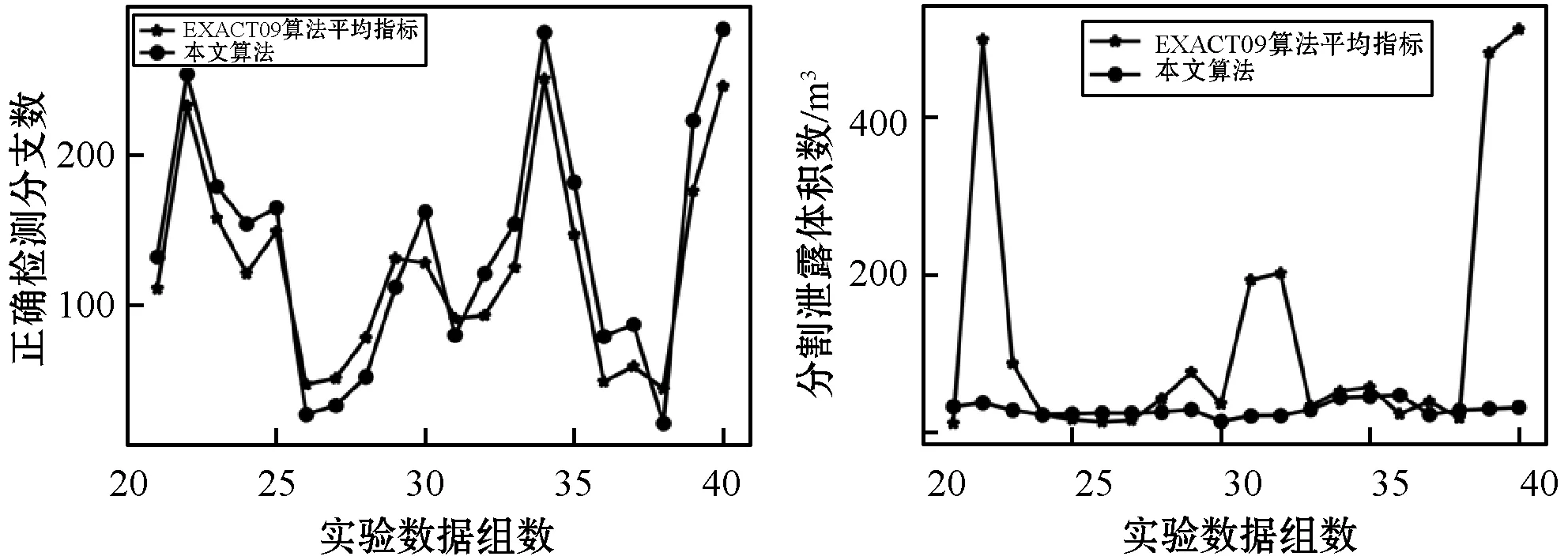
(a) (b)图7 本文算法检测到的分支数与15种EXACT09算法 平均检测分支数对比图
表1为本文算法与EXACT09的15个参赛算法评估结果,显示了不同算法的树长、假阳性概率以及检测到的正确分支数的比例。

表1 使用20个测试用例的平均评估度量 %
图8更直观地显示了不同算法的树长、假阳性概率以及检测到的正确分支概率,其中,(d)为检测到的树长与假阳性率的散点图,显示了不同算法的平均性能。可以看出,本文算法在假阳性极低的情况下可以获得不错的分割结果。
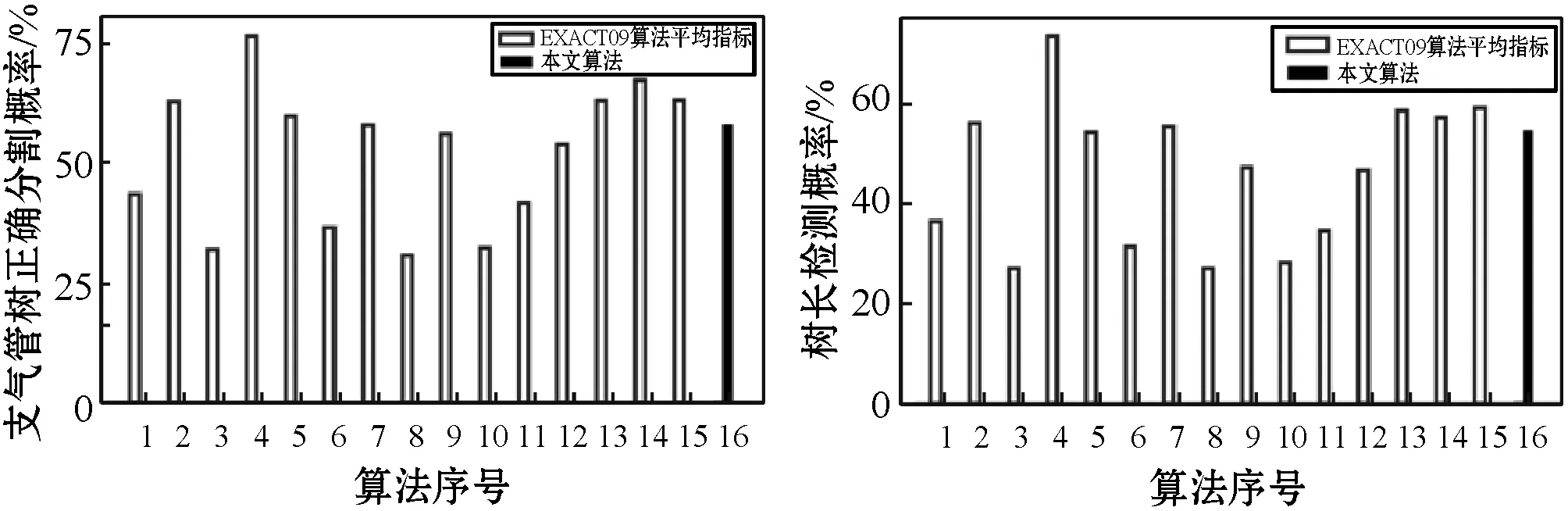
(a) (b)

(c) (d)图8 检测到的树长与假阳性率的散点图
实验结果表明,本文算法与其他三维方法相比,在不依赖于种子点的人工选择,不需要训练集的条件下能获得更完整的肺气管分割结果,且漏泄量更小。
4 结 语
本文提出了一种基于T-prim树的肺气管树分割算法。首先结合区域生长算法与形态学灰度重建,初步分割出肺主支气管。之后改进prim算法,结合一种基于马尔可夫随机场优化的分水岭分割框架,使用T-prim最小生成树算法构造出新的能量函数,利用构造出的T-prim树结合这一优化分水岭分割框架完成对细支气管的分割。通过与EXACT09竞赛算法的对比实验验证了本文算法在不需要手动操作、不需要训练数据的情况下可以获得优秀的分割效果,并且分割过程中的泄露量和错误率非常低。
