一般指派问题的LINGO解法讨论

钱丽丽

(无锡机电高等职业技术学校，江苏 无锡 214000)

引言

在日常生活安排和企业生产管理工作中，经常会遇到给人分派工作或给机器指派任务等一般指派问题。一般指派问题是最优化问题的一种，它的问题模型是给n个人(本文中的人泛指可以执行任务的一切物体)指派完成m项任务，根据每个人完成每项任务的工作效率来研究如何分配任务，使完成任务所消耗的总资源最少或总收益最大。指派问题是0-1型整数规划问题中比较常见的一种，它的特点是决策变量只有0和1两种取值，在问题讨论时，通常把某个人是否执行某项任务取值为1和0，建立一般指派问题与0-1规划对应关系。当指派人数和任务数都比较大或数量关系不对等时，问题的模型就会变得复杂，求解也更加困难。因此，本文引入了LINGO这款软件，LINGO是美国LINDO系统公司专门开发用于求解优化模型的数学软件，主要用于求解线性、非线性和整数优化模型，它内置了一种建立最优化模型的语言，可以简便地表达大规模问题，利用LINGO高效的求解器可以快速求解并分析结果[1]。本文通过对一般指派问题建立0-1规划模型，分析模型，并借助LINGO求解法实现对此类问题的讨论。

目前，一般指派问题根据人数和任务数的数量关系大致有以下三种情况：(1)人数和任务数相等，即每个人必须只完成一项任务；(2)人数小于任务数，一个人可以完成几项任务；(3)人数大于任务数，一项任务可由几个人来完成。其中，第一种指派为标准指派，它是一种最基础的指派，人与任务一一对应；第二、第三种指派属于非标准指派。本文通过具体的案例，给出这三种情况的LINGO解法[2]。

一、标准指派问题

例1：有4个工人，要指派他们完成4项任务， 规定每人只能做1项任务, 每项任务只能1个人做，每人做各项任务所消耗的时间如表1所示，如何分派任务，可使总的消耗时间最少[3]？

表1 任务分配问题

问题分析：这是典型的指派问题，每个工人必须做且只能做1项工作，第i个工人是否做第j个工作可以用0-1型变量表示。所以这类问题的数学模型是0-1型整数规划。

(一)模型建立

1.决策变量

2.目标函数

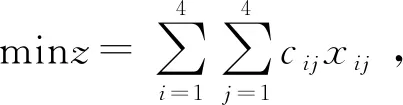
3.约束条件

set:

Worker/1..4/;

Job /1..4/;

Assign(work,job):c,x;

endsets

data:

enddata

min=@sum(Assign:c*x);

@for(worker(i):@sum(job(j):x(i,j))=1);

@for(job(j):@sum(worker(i):x(i,j))=1);

@for(Assign:@bin(x));

(二)模型结果分析

运行结果中的x(i，j)=1表示第i个工人执行第j项任务，x(i，j)=0则表示不执行，故当工人1→任务2，工人2→任务1，工人3→任务3，工人4→任务4，所用的总时间最省，共70小时。

用LINGO求解标准指派问题程序语言比较简单，它的语句顺序可以交换，字母可以不区分大小写，但必须是输入能被软件识别的符号或语言，否则哪怕是一个微小的错误也会导致程序无法运行，所以在编程时除了要按照正常的要求编写外，还应注意一些细节：如变量名只能由字母和数字组成，变量不能出现在约束条件的右端，调用函数必须以符号@开头，函数后面的变量必须加括号等[4]。

二、非标准指派问题

例2：某公司计划开5家新店，并决定由该公司下面的3家建筑公司来负责完成。3家建筑公司Ai(i=1,2,3)对5家新店Bj(j=1,2,3,4,5)的建筑费Cij(i=1,2,3,j=1,2,3,4,5)如表2所示，且允许每家建筑公司承建1家或2家商店，但每家商店只能由1家公司承担，问如何对5家新店分配建造任务，可以使建造费用最小。

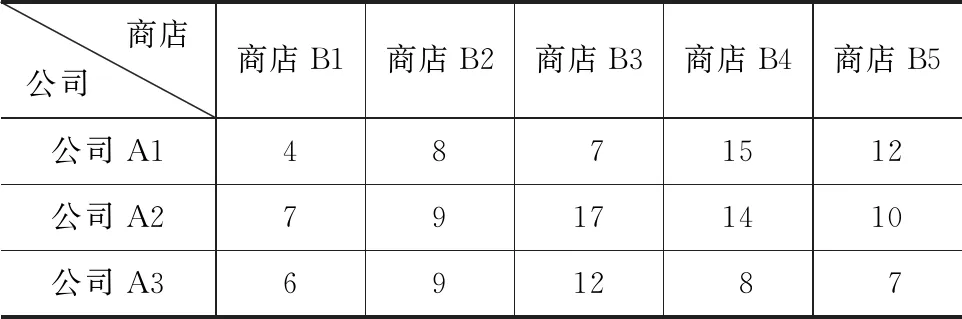
表2 公司承建商店问题 单位：万元

(一)问题分析

由于公司少商店多，且每家公司最多可以承担2家新店，因此，可以把每家公司化作相同的2家公司，然后再添加虚拟的一列B6，各公司承建商店B6的费用均为0，用系数矩阵来表示出这种变化：

B1B2B3B4B5 B1B2B3B4B5B6

用LINGO软件求解

sets:

company/1..6/;

shop /1..6/;

Assign(company,shop):c,x;

endsets

data:

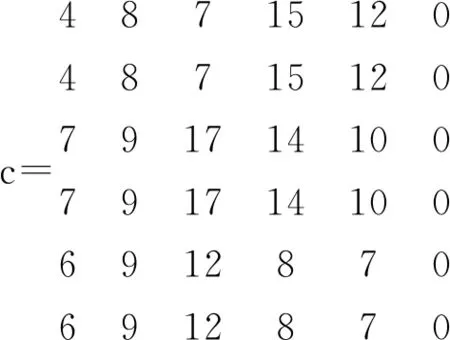
enddata

min=@sum(Assign:c*x);

@for(shop(j):@sum(company(i):x(i,j))=1);

@ for(company(i):@sum(shop(j):x(i,j))=1);

@for(Assign:@bin(x));

运行结果显示出有效数据：x(1,1)，x(2,3)，x(3,6)，x(4,2)，x(5,5)，x(6,4)为可行方案，且最小值为35。为了问题研究的方便，把原来的3家公司假设成了相同的6家，因此，i取1和2、3和4、5和6分别表示公司A1，公司A2，公司 A3，j取1—5表示商店1—商店5，j取6表示没有商店。故当公司A1承建商店B1和B3，公司A2承建商店B2，公司A3承建商店B4和B5时，所消耗的总建筑费用最省，共需35万元。

例3：有6个人甲、乙、丙、丁、戊、戌要翻译日文、韩文、英文和俄文4本书，他们每个人都精通这4种语言，各自翻译1本书所需的时间如表3所示，每个人只能翻译1本书，1本书可以由1个人或2个人来翻译，问如何分配任务，可以使他们总共花的时间最少？

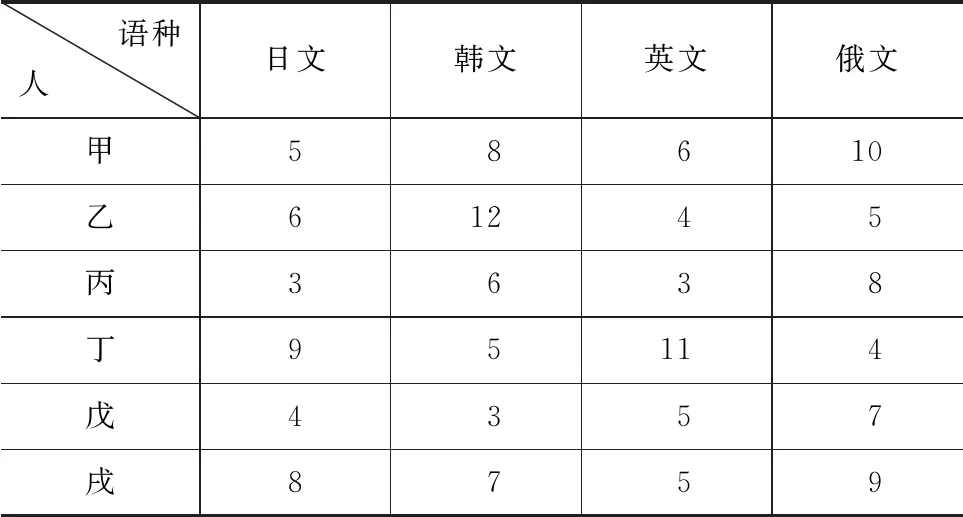
表3 翻译问题

问题分析：1本语言书可以由2个人翻译，可以把每1本书变成2本相同的书，问题可看成6个人翻译8本语言书，缺少的2个人数用虚拟的2个人补足，虚拟的2个人翻译每本书所用的时间为0，用系数矩阵表示出这种变化：

(二)编写LINGO程序

sets:

person /1..8/;

language /1..8/;

Assign(person,language):c,x;

endsets

data:

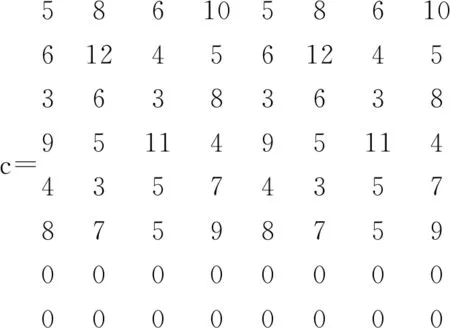
enddata

min=@sum(Assign:c*x);

@for(language(j):@sum(person(i):x(i,j))

=1);

@for(person(i):@sum(language(j):x(i,j))=1);

@for(Assign:@bin(x));

运行程序结果显示，甲和丙翻译日文书，乙和戌翻译英文书，丁翻译俄文书，戊翻译韩文书，6个人翻译8本书的总共时间最少为24小时，由于8本书是原来4本书的叠加，所以6个人翻译8本书所花的时间应该是6个人翻译4本书的两倍，故实际最少时间应该是12小时。

在解决以上两种非标准指派问题时可以通过增加虚拟的“人”或虚拟的“事”来转化为标准指派问题。其中，增设的虚拟人做各种事的费用或产生的效益均为0，同样，增加的虚拟的事被人完成所需的费用或能产生的效益也是0。当然，还要注意的是，几个人完成同一件事的时间并不是他们独立完成这件事时间的简单叠加，所以应根据实际情况对计算结果进行一定分析和处理。

结束语

一般指派问题是生产管理者在日常工作中经常会遇到的一类问题。用LINGO软件求解标准指派问题能更高效地表达目标函数与约束条件，所编的程序语言几乎是对数学模型的翻译，不需要太多的转换,程序结果简洁易懂，即使初学者也能快速掌握。而本文中讨论的两种非标准指派问题最终都能通过一定的条件假设转化为标准指派问题来求解。当然，还有一些其他的非标准指派，如限定某人一定不能做某项工作或者必须做某项工作的情况更为复杂，不属于一般的范畴，这里就不作深入讨论了。