基于理解，问题引领，学会学习——以“反函数的概念（第一课时）”为例

◎ 徐庆惠 胡晓丽

视频课与以往的常规教学课有着较大的区别，对教师和学生都是一种新的挑战，其中最大的挑战是教师授课时间的缩短和没有学生的课堂。因此，在教学设计时需要关注的是，如何合理设计整节课的教学环节来实现教学目标，如何通过问题链的设置来引导学生开展自主学习。另外，教学内容既要通俗易懂又能体现数学学科本质。为了提升教学效率，在每节课的教学设计时还需要关注整体性和局部性，连贯性和延续性。既要考虑该节课所在单元的整体结构，其核心的理念在该节课中如何体现，又要考虑如何将该单元中的核心知识、核心素养与其他单元保持连贯和延伸。

本文以“反函数的概念”的第一课时为例，是对视频课的教学模式的初步尝试与探索。

一、教学设计

（一）教学设计说明

函数和反函数从不同的角度反映了一组对应关系的两种相反的对应法则，虽然函数与其反函数一般情况下是不同的，但它们在对应关系上却是统一的，体现了辩证统一的关系。本节课通过创设情境引入课题，激发学生的学习兴趣，愉快地参与。在形成概念及理解辨析环节中设置问题链，促进学生思考和探索。在例题讲解，巩固新知环节，引导学生有逻辑的规范表达。在课堂练习环节，给学生一定的时间完成，然后给出答案，便于学生及时检测学习效果。课后作业分基础练习和能力拓展，基础练习面向全体学生，能力拓展供学生根据自己的实际情况选做。

（二）教学内容分析

本节课是沪教版《数学》（高一年级第二学期）中第四章第五节“反函数的概念”的第一课时。反函数的概念与函数的概念有着紧密的联系，通过创设游戏情境引入反函数的概念，进而理解反函数的概念以及学会求给定函数的反函数。反函数的学习既可以加深对函数概念的进一步理解，又为后续对数函数、反三角函数的学习做好准备，起到承上启下的作用，同时有助于发展逆向分析问题、解决问题的能力。

（三）教学目标

（1）通过创设游戏情境引入反函数的概念，理解反函数的概念，提高学习数学的兴趣，经历数学的抽象与概括过程，提升把握事物本质的能力。

（2）会判断一个函数是否存在反函数，掌握求反函数的基本步骤，理解函数与其反函数之间的内在联系。

（四）教学重点及学习难点

（1）教学重点：反函数的概念与反函数的求法，函数与其反函数之间的内在联系。

（2）学习难点：理解反函数的概念，反函数定义域的确定。

（五）教学过程

1. 创设情境，引入课题

请你任意想出一个实数，依次把它乘以2，加上100，除以5，减10，最后除以2。把结果告诉我，我就能知道你所想的这个数。

2. 理解概念，进行辨析

（1）反函数的概念。

（2）函数与其反函数的关系。

【问题1】已知函数y=f（x），它的定义域是D，值域是A，记它的反函数为y=f-1（x），那么函数y=f-1（x）的反函数是什么？

【问题2】函数y=x2+1（x∈R）是否存在反函数？

【问题3】如果函数y=f（x），x∈D 存在反函数，那么该函数应具备什么样的特征？

【问题4】函数y=f（x）的定义域、值域与它的反函数y=f-1（x）的定义域、值域有什么联系？

3. 讲解例题，巩固新知

例1 判断下列函数是否存在反函数。

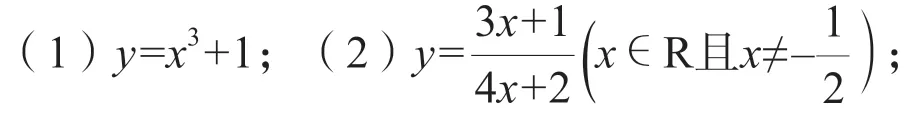
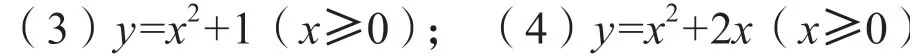
例2 求下列函数的反函数（即例1 中的4个函数）。

第（4）题变式：求函数y=x2+2x（x≤ –2）的反函数。

小结：求函数反函数的步骤。

例3 设a∈R，若函数f（x）=x2–2ax+5，x∈[1，2]存在反函数，求a 的取值范围。

本节课学习了反函数的概念，需要注意的是，不是每一个函数都存在反函数，对于函数y=f（x），x∈D，其存在反函数的条件为x 与y 一一对应。求函数的反函数有三个基本步骤：第一步“求”，第二步“解”，第三步“换”。反函数的定义域不是由反函数的解析式确定的，而是由已知函数的值域确定的。

二、学习建议

在线视频课对师生而言，都是一种全新的教与学的模式。在这种新模式下建议学生做到课前自主阅读，课内同步思考，课后归纳整理。新模式意味着学习方式的改变，但在改变中逐步学会自主学习，未尝不是提高学习效率的良好契机。

课前自主阅读就是预习，对于新课的预习，以阅读教材为主，尤其是本节课概念、公式或定理的阅读。比如本节课是反函数的概念，在反函数的概念阅读中，可以结合函数的概念，关注“任意”“唯一确定”等关键词以及反函数的记号等。例题的阅读，要关注解题步骤的逻辑性、表达的规范性等。在阅读的过程中还可以记录下存在的疑问，思考教材边注中提出的问题。

听课时，要关注教师对概念的讲解以及课前阅读中产生的疑问，对于教师提出的问题，要积极思考，并适当做些补充内容，如例题的笔记、思考题等。课后要及时整理笔记、完成作业，复习巩固，为下一课时的学习打好基础。有兴趣的学生还可以查阅与这节课有关的数学史等资料，增加知识面的同时，还可以加深对概念的理解。

【专家点评】

本节课设定的教学目标科学、合理，既体现教材要求，又符合学生实际。考虑到在较短的教学时间内要达成教学目标，在反函数概念的引入环节，设计了简单而熟悉的小游戏，从中抽象概括出反函数的概念，体现了对应思想。针对视频课的“保底”性质，在帮助学生进一步理解概念的过程中，巧设问题链，由浅入深，结合例题的分析与适当变式，从是否存在反函数到如何求反函数，逐步揭示了反函数概念的本质，并归纳总结求反函数的方法。课后分层作业的设计，还考虑到满足不同学生的需求。

在课堂教学中，教师的表述准确、生动、流畅、亲切，板书规范，在层层递进的教学中，突出重点内容，讲练结合，学生既可以独立思考，也可以在课后继续探索。学生不仅在数学抽象素养和逻辑推理素养上得到发展，而且在自我管理和自主学习方面也得到提升。

（点评专家：徐庆惠 上海市黄浦区教育学院）