基于新的计算四分位数公式的箱图绘制

2020-04-16赵晓进赵晓芳邵立杰胡李裔

唐山师范学院学报 2020年6期

赵晓进，赵晓芳，邵立杰，胡李裔

（郑州工商学院商学院经济系，河南郑州 451400）

1 引言

SPSS 是一个非常权威的、世界公认的著名统计软件，近十年来以令人惊讶的速度在国内得到了迅速普及[1,2]。SPSS 箱图是利用5 个基本统计量和极端值来描述样本数据分布的一种统计学方法，描述定量变量的数据分布[3]。箱图图示简单，既可以直观地识别数据中的极端值，又可以通过观察四分位数的对称情况来初步判断数据的偏态情况，还可以比较几组数据之间的分布差异等[4]。目前，在许多高等院校的社会统计学教材中，很少有SPSS 箱图绘制的详细介绍。教学实践中，学生很难根据教材上的公式绘制出箱图，使得箱图应用受到限制。另外，不同教材中给出的四分位数计算公式也不完全一致，使用频率最高的四分位数的计算公式[5]见(1)和(2)：

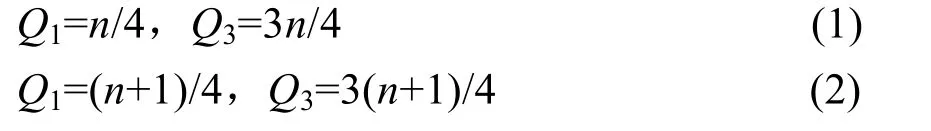
当样本数量较大时，可以用上述公式计算四分位数；但当样本数量较小时，使用上述公式计算四分位数的结果与SPSS 统计软件上的计算结果有差异。本文提出一种新的计算四分位数的方法，计算结果与从SPSS 统计软件绘制的箱图中读取的结果一致。

2 箱图的绘制原理

典型的箱图的基本构成包括极端值、奇异值、本体最小值、下四分位数（Q1）、中位数（Q2）、上四分位数（Q3）和本体最大值。箱图的主体是中间的矩形框，Q1、Q2、Q3三条线分别表示相对应的变量值第P25、P50、P75 的百分位数，变量50%的观测值落在这一区域。箱图中间的纵向直线构成箱体的上下两条端线，端线的两端分别是本体最小值和本体最大值。

2.1 新公式的给出

首先用全距计算出Q2，然后以Q2为中心再计算出Q1和Q3。由于奇数个数据和偶数个数据的计算公式不同，下面分别描述。

2.1.1 偶数个数据计算公式

当处理的数据是偶数个时，使用下列公式：

Q2=(n+1)/2

Q1=(Q2+0.5)/2

Q3=(Q2-0.5)+Q1

2.1.2 奇数个数据计算公式

当处理的数据是奇数个时，使用下列公式：

Q2=(n+1)/2

Q1=(Q2+1)/2

Q3=(Q2-1)+Q1

2.2 箱图绘制步骤

（1）将原始数据从小到大进行排序。

（2）根据2.1 公式分别计算出描述四分位数位置的Q1、Q2和Q3的位置。

（3）根据Q1、Q2和Q3的位置分别计算出相对应的四分位数的变量值，即P25、P50 和P75。

（4）根据四分位数的变量值（P25、P50 和P75）计算出内距（QR）。然后根据内距计算出1.5 倍QR 和3.0 倍QR。在1.5 倍QR 与3.0 倍QR 之间的区域为奇异值区域，大于3.0 倍QR 的区域为极端值区域。一般情况下，在箱图的上下方都会有奇异值和极端值分布。但是，有些情况下奇异值和极端值只分布在箱图的一端或者两端都没有[3]。

（5）最后根据四分位数、奇异值和极端值的分布绘制出箱图。

3 案例分析

案例1 某城市随机抽取了10 个家庭，每个家庭人均月收入数据见表1，试计算出相关的四分位数及变量值并绘制箱图。

该案例中数据个数为偶数，根据上述偶数个数据计算公式分别计算出绘制箱图的主要数据，见表2。根据表2 数据绘制箱图，见图1。

结合表1、表2 和图1 可以看出，该案例中最小值为3 100，下四分位数为3 400，中位数为3 700，上四分位数为4 500，最大值为7 000。从图1 可看出，箱图上端的第10 个数据是7 000 元，该数据大于1.5 倍QR 的上界值6 150，小于3.0倍QR 的上界值7 800，落在箱图上端的奇异值区内，所以构成箱图上端的奇异值，用圆圈表示。从图1 还可看出，该案例中箱图下端没有的奇异值和极端值。

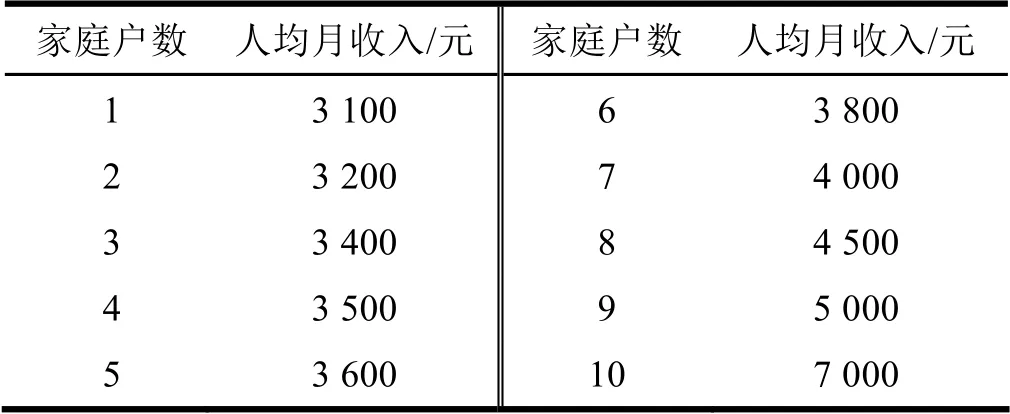
表1 某城市10 户家庭人均月收入资料

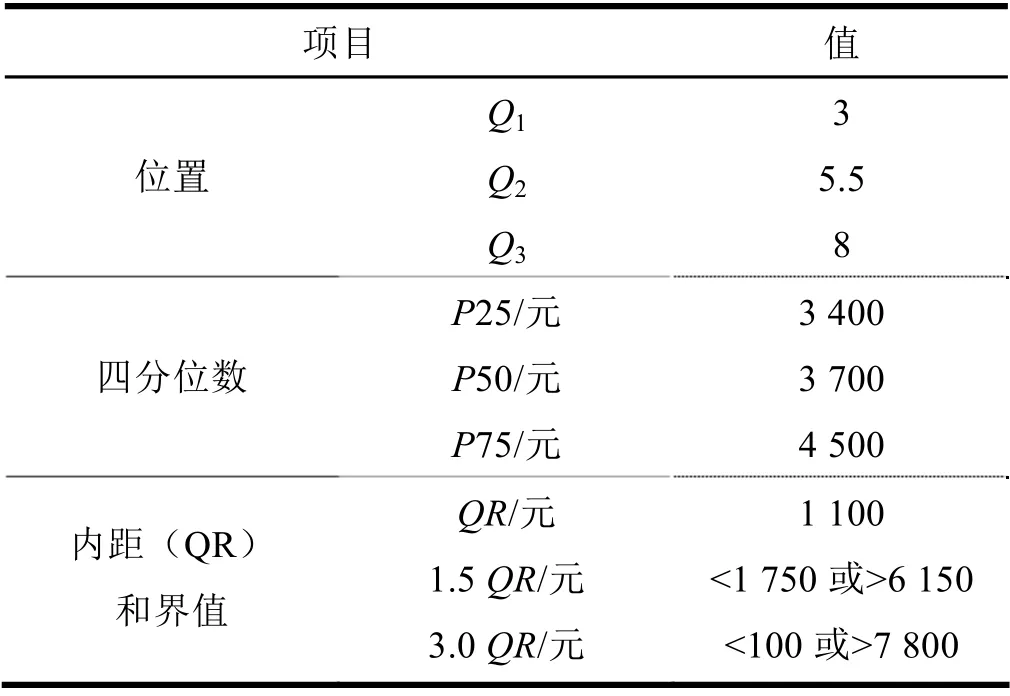
表2 案例1 主要计算结果

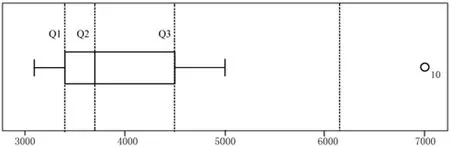
图1 案例1 资料绘制的箱图

案例2 某工厂某班组11 名工人日生产产品的零件数资料见表3，计算出相关的四分位数及变量值并绘制箱图。

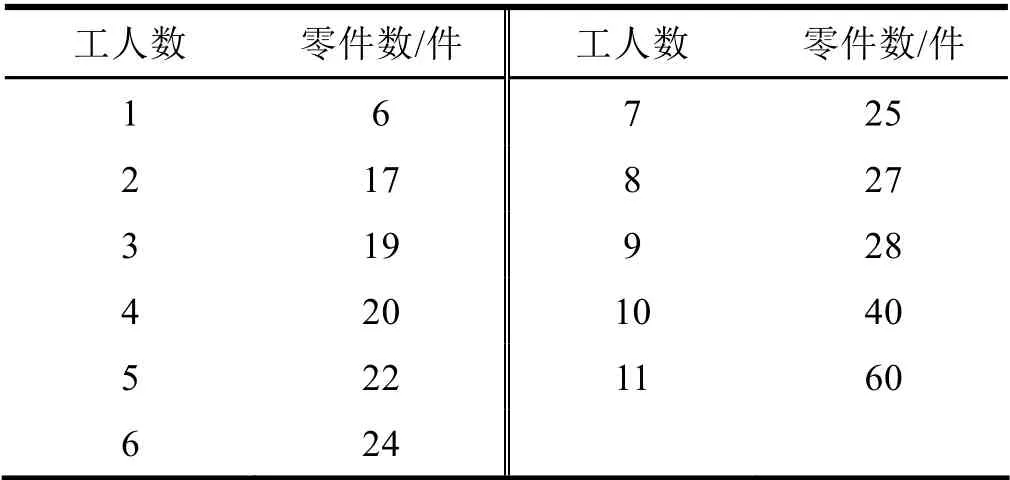
表3 某工厂某班组11 名工人日生产产品零件数资料

该案例中数据个数为奇数，根据上述奇数个数据计算公式分别计算出绘制箱图的主要数据，见表4。

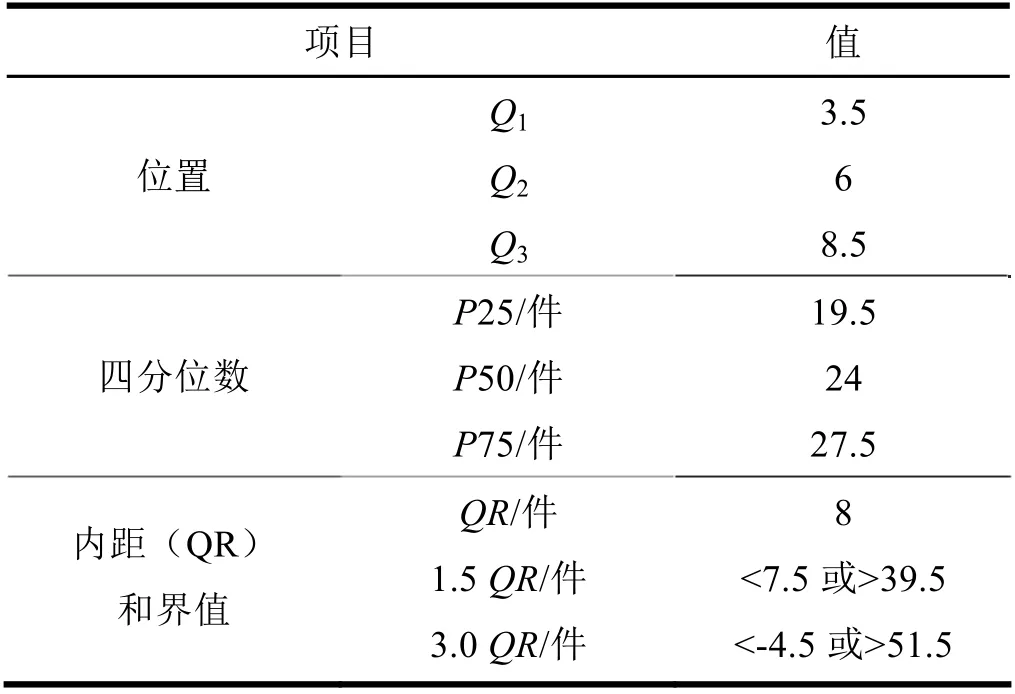
表4 案例2 的主要计算结果

根据表4 数据绘制箱图，见图2。

图2 案例2 数据绘制的箱图（图中的数据表示资料排序后的位置序号）

结合表3 表4 和图2，可以看出该案例中最小值为6，下四分位数为19.5，中位数为24，上四分位数为27.5，最大值为60。第1 个数据是6，小于1.5倍QR下界值7.5，大于3倍QR下界值-4.5，落在下端的奇异值区内，构成箱图下端的奇异值，用圆圈表示。第10 个数据是40，大于1.5 倍QR的上界值39.5，小于3.0 倍QR 的上界值51.5，构成箱图上端的奇异值，用圆圈表示。第11 个数据是60，大于3 倍QR 的上界值51.5，所以落在箱图极端值区内，构成箱图上端的极端值，用星号表示（见图2）。