饱和砂砾土的孔压发展模式试验研究

杨 哲 张 婷 王占彬 何晓民 肖志威

(长江科学院水利部岩土力学与工程重点实验室，湖北武汉 430010)

0 引言

循环荷载作用下饱和砂土和砂砾土等无黏性土振动孔压的增长对其抗液化强度、变形特性等具有明显影响。近年来国内外相关学者对砂土振动孔压的发展特性进行了大量的研究工作，相关研究成果对砂砾土振动孔压增长模式的研究具有重要的参考价值。然而，由于土界条件和地震波特性的影响，若直接套用砂土振动孔压模型对砂砾土振动孔压的发展进行模拟预测，很可能产生较大的误差。振动孔隙压力增长方式的选择，将对砂砾土基础工程地震计算结果的可靠性和准确性产生明显的影响。因此，开展砂砾土振动孔压发展模式的研究，以满足不同土性条件下的土工抗震问题是十分有必要的。

预测不同条件下土体在地震荷载下振动孔压的发展规律直接影响着土体的稳定性评估。国内外学者就振动引起孔隙水压力增长及其发展过程做了大量工作，提出了一些计算方法和公式。对于砂土材料，依据孔压模型考虑的因素可分为：应力模型、应变模型、能量模型等。如Seed等[1]依据饱和砂土等压固结不排水动三轴试验的结果，用以寻求无量纲化的孔压和振次的关系，提出了反正弦孔压应力模型；Finn等[2]将Seed孔压模型推广到各向不等压固结情况；Martin、Finn、Seed等研究了饱和砂土在不排水条件下孔压的增量与其在排水条件下体积应变的增量之间的规律，得到振动孔压的应变模型[3]；曹亚林等[4]根据标准砂的试验分析认为，孔压的升高与土粒重新排列过程中所耗损的能量有关，得出了孔压和能量之间的振动孔压能量模型。

目前饱和砂砾土的孔隙水压力模型主要借鉴于饱和砂土的相关研究成果。砂砾土由于在成分上含有砂砾石，导致与砂土存在较大的差异，因此不能简单地把砂土的振动孔压发展规律应用于砂砾土。借鉴以往的研究方法和研究成果，本文对相关研究成果进行了总结归纳，并研究了不同级配试样孔压变化规律，提出了相应的孔压发展规律表达式，为砂砾土地基工程的地震反应分析提供一定的参考。

以砂砾土为研究对象，进行了砂砾土不排水循环三轴试验，研究了饱和砂砾土在动荷载作用下的孔压发展模式。

1 试验设备和土样

液化特性试验利用GDS动三轴完成，试验数据由计算机采集与处理，由压力室试件下方激振器激振，试验选用激振频率为0.1 Hz、1.0 Hz和2.0 Hz，选用动荷载波形为正弦波，试件尺寸为φ101 mm×H200 mm。

试验采用多层湿法制备重塑砂砾土试样。试验采用4种级配编号分别为JP1、JP2、JP3、JP4，砾石含量分别为80%、70%、60%、50%。4种级配的颗粒组成、制样基本指标和基本物理性指标见表1、表2和表3。试验均是按《土工试验规程》(SL 237—006—1999)[5]和《水电水利工程粗粒土试验规程》(DLT 5356—2006)[6]规定的方法进行的。

表1 砂砾土试样级配颗粒组成

表2 砂砾土试样基本指标

表3 砂砾土试样级配物理性指标

2 试验方案

为了研究含砾量和振动频率的差异对砂砾土液化特性的影响，本文以4种不同级配的砂砾土进行以下多种不同试验。具体试验方案如表4所示。

本动三轴试验选取首次出现孔隙水压力增量达到初始有效固结围压作为等压固结饱和砂砾土的液化破坏标准，轴向应变峰值达到5.0%作为非等压固结饱和砂砾土的破坏标准。

表4 砂砾土试验方案

3 试验结果

3.1 饱和砂砾土振动孔压应力模型

图1(a)(b)(c)分别为典型砂砾土的等压固结不排水动三轴试验中轴向应力σd、振动孔压ud、动应变εd随振次N的典型变化曲线，随着循环次数的增加，轴向应变逐渐累积，振动孔压也随循环荷载的波动而周期性地起伏变化，同时振动孔压不断累积。当振动孔压上升接近初始有效围压的同时，轴向应变迅速增加，直至试样发生破坏。另外，振动孔压在一个应力循环过程中振动孔压的波动也随循环荷载的施加而发生变化，从图1(b)中的振动孔压的时程图可看出，当循环荷载开始施加时，单个循环荷载内的孔压波动幅值逐渐增大；当振动孔压累积至0.8倍的初始有效围压后，单个循环荷载内的孔压波动幅值呈现减少的趋势。

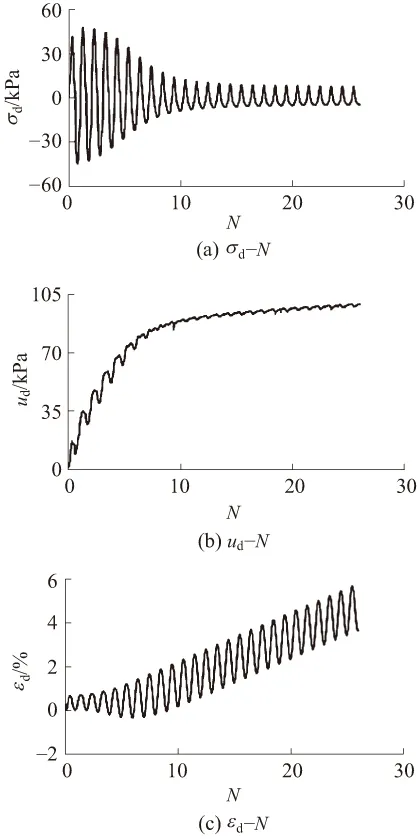
图1 典型砂砾土动力参数与振次关系曲线

振动孔压幅值的变化是由于砂砾土初次承受循环荷载时，粒径较大的砂土、砂砾石与粒径小的砂颗粒间相互错动和滑移，同时部分颗粒在受荷作用下破碎，导致土体的孔隙比发生变化，使得土体的渗透性产生变化，振动孔压波动幅值增大；随着残余应变的累积、振动孔压的上升，较小颗粒的有效应力渐渐丧失并逐渐悬浮在由较大粒径土体构成的“骨架”中(较大粒径颗粒质量较大，难以悬浮)，振动孔压的波动幅值逐渐减少后保持不变。

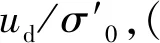
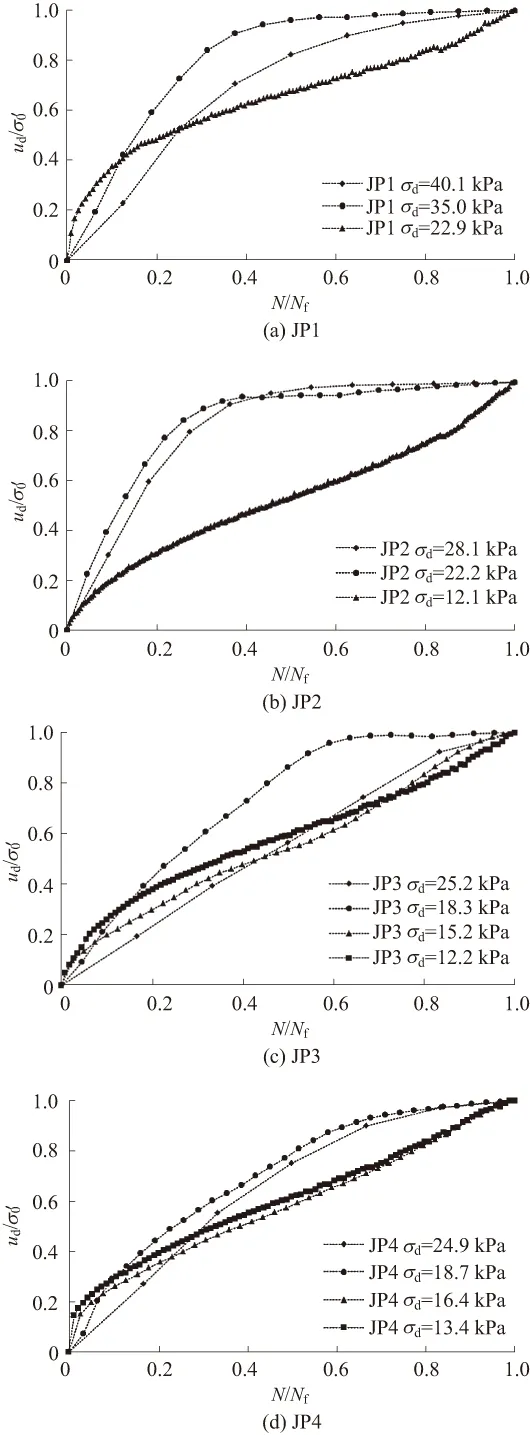
图2 饱和砂砾土孔压比与振次比关系曲线

图3 不同频率下级配JP3饱和砂砾土孔压比与振次比关系曲线

从总体上看，在动应力幅值较大时，随着循环应力的增大，孔压比ud/σ′0与振次比N/Nf曲线的形状从“S”型曲线向抛物线型发展，这与张建民和谢定义[7]提出的B型曲线向A型曲线转变的结论相符。可将其孔压增长曲线分为抛物线型、类抛物线型和“S”型。

“S”型的孔压比增长曲线，采用Seed等[1]提出的孔压模型进行拟合，拟合效果较好，拟合曲线与实测的动孔压比增长曲线如图4所示，其中试验常数θ取值1.25，与Seed等提出的大多数情况下的θ值0.7相差较大。通过采用徐 斌等[8]提出的砂砾料的孔压模型(1)进行拟合，也取得不错的拟合效果，拟合曲线与实测的动孔压比增长曲线如图4所示，其中试验常数θ取值0.65(徐 斌等建议取值θ=0.475)。由Seed孔压模型参数θ的取值差异可见，饱和砂砾土与一般砂土的振动孔压发展规律差别较大。

(1)

式中：uf为试样破坏时的孔压值，Nf为破坏振次。

图4 “S”型模型计算的动孔压比增长曲线与试验结果对比

而其中动荷载较大(多数情况下试验控制的动荷载为20～30 kPa)时，呈抛物线型或类抛物线型的孔压比曲线可用曹宇春等[9]提出的孔压模型公式(2)进行拟合，但抛物线型采用陈国兴和刘雪珠[10]提出的双曲线模型(3)进行拟合，其模型公式为：

(2)

式中：σ′c为初始有效固结压力；Nf为相应于振动破坏时的循环振次；a、b为试验参数。

(3)

式中：uf为达到振动破坏时的振动孔隙水压力；Nf为相应于振动破坏时的循环振次；a，b为试验参数。

拟合效果较好，图5为对抛物线型的动孔压比增长曲线进行拟合，得到公式(2)拟合参数a=1.70，b=0.029，公式(3)拟合参数a=0.10，b=0.90；图6为对类抛物线型的动孔压比增长曲线进行拟合，得到公式(2)拟合参数a=1.15，b=0.21，公式(3)拟合参数a=0.32，b=0.68。

从图5和图6可得出，含砾量对砂砾土的振动孔压发展模式存在的影响规律如下所述：含砾量分别为80%和70%的级配JP1和级配JP2以抛物型振动孔压发展模型为主，含砾量分别为60%和50%的级配JP3和级配JP4以“S”型振动孔压发展模型为主，图4中级配JP1的动孔压比基本以直线形式增长，含砾量越高孔隙水压力前期增长越快。不同级配破坏振次相近的动孔压比增长曲线见图7，可以看出级配JP1和级配JP2为抛物型孔压增长模式，级配JP3和级配JP4为类抛物型孔压增长模式，原因可能为粒径较大颗粒含量越多，试样内部颗粒之间的孔隙总数越少，孔隙水压力越容易上升。

图5 抛物线型模型计算的动孔压比增长曲线与试验结果对比

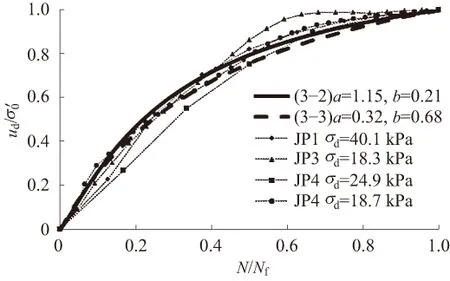
图6 类抛物线型模型计算的动孔压比增长曲线与试验结果对比

图7 不同含砾量动孔压比与振次比关系曲线

级配JP3不同振动频率下动孔压比增长曲线(破坏振次相近)见图8，当振动频率为0.1 Hz时，增长曲线呈近“S”型增长模式，振动频率为1.0 Hz和2.0 Hz时为类抛物型增长模式，说明振动频率越小，孔压增长的速度越慢。

图8 不同振动频率动孔压比与振次比曲线

3.2 饱和砂砾土振动孔压应变模型

孔压应变模型的共同特点是将动孔压同某种应变(体积应变或轴向应变)联系起来[3]。其中Martin-Finn-Seed[11]和汪闻韶[12]是将不排水时土体的孔压与排水时土体的体积应变相联系，分别提出了各自的孔压模型。另外，还有学者主张采用剪应变，即将不排水时土体的孔压与轴向应变(或剪应变)相联系，如Lo的研究将孔压表达为大主应变ε1的单调函数[3]；Dobry等[13]的研究发现，循环荷载下饱和砂土的孔压增长与循环剪应变γd有很好的相关性，并存在一个残余孔压发展的门槛剪应变γt，当γd≤γt时，试样内不产生残余孔压[3]。

由砂砾土的动三轴试验结果发现，饱和砂砾土在循环荷载作用过程中振动孔压的周期性变化与轴向应变同样息息相关。

定义剪应变比为：

Rγ=γ/γf

(4)

式中：γ为振动次数为N的双幅轴向剪应变；γf为试样破坏时的双幅轴向应变(轴向应变峰值达到5%时，采用此时5%轴向应变对应的剪应变)。

图9—图12分别为4个不同含砾量饱和砂砾土动孔压比ud/σ′0与剪应变比γ/γf关系曲线，通过对试验结果的分析，该孔压模型可以表示为公式(5)：

(5)

式中：ud为振动次数为N时的峰值动孔压，σ′0为振前试样45°面上的有效法向应力，即初始有效固结压力，P2为含砾量，a和b为试验常数，在本文试验中取a=1.2，b=0.4。

该孔压应变模型在中后期阶段可以较好地拟合不同含砾量饱和砂砾土在振动荷载作用下的孔压发展模式。在前期阶段因非零的初始动剪应变值与零点间隔较大，造成该模型前期拟合效果没有中后期阶段拟合效果好，这主要是因为所采用的应变值是每周次循环荷载时试样出现轴向应变幅值，导致第一个非零点与零点之间相差较大。

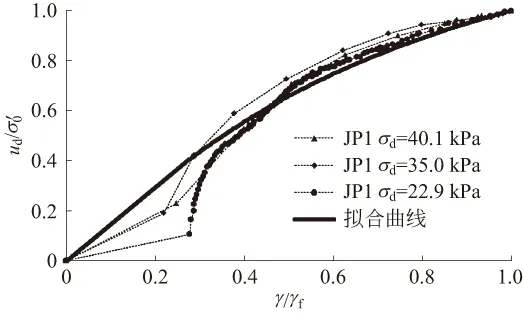
图9 JP1孔压比-应变比关系曲线与拟合曲线

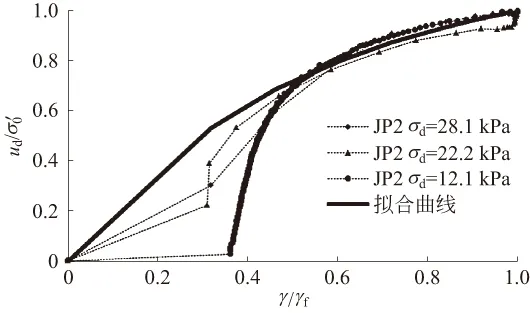
图10 JP2孔压比-应变比关系曲线与拟合曲线

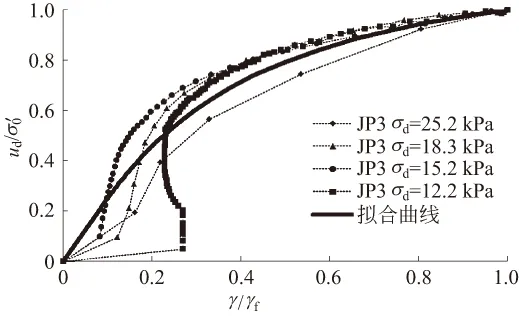
图11 JP3孔压比-应变比关系曲线与拟合曲线

图12 JP4孔压比-应变比关系曲线与拟合曲线

图13—图15分别为振动频率为0.1 Hz、1.0 Hz、2.0 Hz条件下的饱和砂砾土动孔压比与剪应变比关系曲线，通过对试验结果的分析，得到含有频率f参数的孔压应变模型(6)：

(6)

式中：a、b和c为试验常数；f为振动频率，由试验得出参数取值a=0.79、b=0.4、c=0.41。

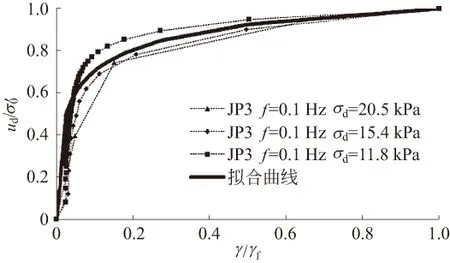
图13 孔压比-应变比关系曲线与拟合曲线(JP3,f=0.1 Hz)

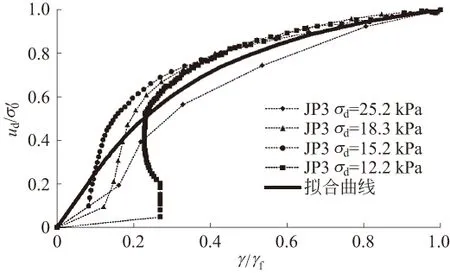
图14 孔压比-应变比关系曲线与拟合曲线(JP3,f=1.0 Hz)

图15 孔压比-应变比关系曲线与拟合曲线(JP3,f=2.0 Hz)

该模型可以较好地拟合不同振动频率饱和砂砾土在振动荷载作用下的孔压发展模式。

4 结论与建议

对现有的孔压模型进行分类概括，针对饱和砂砾土进行不同含砾量和不同振动频率的液化试验，通过对试验数据的整理分析，结论与建议如下：

(1)对于砂砾土试样，含砾量越高，孔压增长越快；振动频率越高，孔压增长越快。

(2)砂砾土孔压时程曲线分为抛物线型、类抛物线型和“S”型三种型式，对抛物型和类抛物型孔压增长曲线采用曹宇春等提出的孔压模型和陈国兴等提出的双曲线模型进行描述，对比其拟合效果，发现抛物型孔压增长曲线采用曹宇春等提出的孔压模型拟合较为理想，并给出相关试验参数值；对“S”型曲线采用Seed反正弦孔压模型和徐 斌的砂砾料孔压模型进行描述，给出相关试验参数值。

(3)振动孔压比与循环剪应变比存在一定联系，参考曹宇春等提出的孔压应力模型提出适用于不同含砾量的孔压应变模型，并计算出相关试验参数值；由不同振动频率饱和砂砾土液化试验，将振动频率引入孔压应变模型，并计算出相关试验参数值。