人民币汇率和股票价格关系的实证研究

徐若锦 郭正晰 吴强

【摘要】汇率和股票价格是反映金融市场和实体经济的两个重要指标。本文使用MGARCH-BEKK模型， 通过分析1991年1月至2019年9月期间美元兑人民币在岸汇率和上证指数的数据，研究了人民币汇率和股票价格之间的关系。研究结果显示股票价格对于人民币汇率有波动溢出效应，这说明股市的波动对于人民币汇率的波动存在影响。

【关键词】汇率  股价  MGARCH-BEKK模型  KPSS检验  Engle-Granger方法

一、引言

汇率和股票价格是反映金融市场和实体经济的两个重要指标。中国已成为当今世界GDP排名第二的经济体，人民币的汇率对世界市场有深切的影响。与此同时，中国A股总市值达到7.22万亿美元，已经成为了世界第二大股票市场。2005年，摩根斯坦利资本国际公司推出了MSCI中国A股指数，也表明中国股市受到全球投资者的关注。因此，中国的汇率和股价是全球投资者关注参考的两个重要指标。

汇率和股价之间的关系一直是经济金融业的重要课题。在过去的几十年中，中国的货币政策经历了几项重大变化。特别是自2005年7月以来，中国政府宣布实行以市场供求为基础，参考一篮子货币进行调节的浮动汇率制度。汇率的波动和市场的關联性显著加强。从2005年7月到2007年4月，人民币对美元汇率经历了持续的大幅上涨。同期，我国股票市场也经历了相似的大幅的上涨。汇率和股价二者同期的变化呈现出一定的关联。

本文旨在寻找中国汇率与股票价格之间的长期关系。文章使用回归条件异方差 （Multivariate Generalized Autoregressive Conditional Heteroskedasticity， MGARCH） 模型的一种特殊形式，MGARCH-BEKK模型， 通过分析1991年1月至2019年9月期间美元兑人民币在岸汇率和上证指数的数据，研究了人民币汇率和股票价格之间的关系。研究结果显示，股票价格对于人民币汇率有波动溢出效应，说明股市的波动对于人民币汇率的波动存在的影响。

文章主要分为五个章节，第一章介绍了本文的背景和研究内容，第二章回顾了国内外相关研究成果，第三章介绍MGARCH-BEKK模型，第四章是结合数据的实证分析，第五章给出研究结论。

二、相关文献

国内外学者对于汇率和股票价格之间的关系进行过很多研究，并得出了不同的结论。

Abdalla 和Murinde采用了印度，韩国，巴基斯坦，菲律宾四个亚洲国家的数据，通过BVAR等经济模型分析了汇率和股市之间的相互关系。结果显示，除菲律宾以外，所有国家中汇率对股票价格都具有因果关系。Aggarwal 研究了浮动汇率制度下美国股价和汇率之间的关系。Aggarwal分析了1974年至1978年美国股价及汇率的数据。结果显示股票价格及汇率之间存在正相关的关系。这种正向关系表明了相比起对于股票价值的低估可能带来的有利影响，汇率下降的短期影响对于美国资本市场来说更加重大。Roll通过对24个国家金融市场的研究得出结论，认为对于大多数国家来说，股市和汇率价格之间有负相关的关系。作者表示这种负相关性与货币当局以抵消全球冲击对当地产业影响为目的，对外汇市场进行的干预政策有关。

Hua Zhao通过分析1991年至2009年人民币汇率和上证指数之间的关系，得出结论，认为外汇汇率和股市之间没有长期均衡的关系。外汇汇率和股票价格之间没有均值溢出效应，但存在双向波动溢出效应，过去的股市创新对于外汇市场未来的波动有重大影响，反之亦然。张兵等研究了中国2005年8月至2007年9月的人民币汇率和上证指数分析了2005年汇率制度改革后汇率与股市的关系及传导机制。结论为汇率和股价之间存在长期均衡的协整关系，且具有稳健性。赵进文等引入风险溢价因素，分析了人民币汇率，短期国际资本流动，货币供给和股票价格之间的动态关系。研究表明，人民币汇率升值会导致短期股票价格下跌。

以上文章对于不同国家不同时期的数据进行研究，对于股票价格和汇率之间的关系进行了分析，并给出了不同的阐释。本文将通过分析中国从1991年1月到2019年9月的数据，研究人民币汇率和股票价格之间的长期关系。

三、研究方法

本文将采用多元广义自回归条件异方差 （MGARCH）模型的一种特殊形式，MGARCH-BEKK模型，来研究汇率和股价之间的关系。

为了检验外汇市场到股票市场的波动溢出效应，需要检验系数c12和g12是否在统计上显著区别于零。检验股票市场到外汇市场的波动溢出效应时，需要检验系数出c21和g21是否统计上显著区别于零。若得出外汇和股票市场之间没有波动溢出效应，则参数c21、g21、c12和g12不会统计上显著区别于零。本文通过似然比统计量λ来检验波动溢出效应：

四、实证分析

本文目的是研究人民币汇率和股票价格之间的关系。文章利用StatsModel、Pandas等Python工具包和 MFE[10]等MATLAB 工具包，分析数据，进行实证研究。

（一）研究数据

本文使用的研究数据为1991年1月到2019年9月期间，美元兑人民币（USD-CNY）在岸汇率及上证综合指数（SSEC）的月数据，共345组数据。人民币汇率数据来自于英为财情，上证指数来自于网易财经。

对于人民币汇率，一方面，美元是国际市场的主要计价和交易货币;另一方面，在岸汇率数据比离岸汇率数据的时间更长，数据更丰富，所以本文选取了美元兑人民币的在岸汇率作为分析指标。

对于股票价格，上证综合指数由上海证券交易所内全部上市股票进行计算得出，具有广泛代表性，能较好地反应股市的整体情况，所以选用上证综合指数代表股价。

图1展示了1991年1月到2019年9月美元兑人民币汇率和上证指数走势图，其中蓝色曲线为人民币对美元汇率，黄色曲线为上证综合指数。图1中，美元兑人民币汇率的走势可以分为四个阶段：第一阶段：1991年至1994年，人民币汇率缓慢上升。在这一阶段，人民币汇率由国家外汇管理局指定并公布，总体呈现缓慢上升趋势。第二阶段：1994年到2005年，人民币汇率经历了急速上涨，之后保持稳定。1994年，中国进行浮动汇率制改革，取消双重汇率制度，实施以市场供求为基础的，单一的，有管理的浮动汇率制度。新政策实施后，1994年人民币汇率经历了大幅上涨，从5.7上涨至8.7。此后，汇率稍有下滑，1995年之后一直保持在8.27至8.28之间。第三阶段：2005年到2014年，人民币汇率缓慢下跌。2005年7月，中国开始实行以市场供求为基础，参考一篮子货币进行调节的浮动汇率制度。政策实施后，外国资本对中国经济与其良好，人民币呈现升值趋势，汇率从8.3下跌到6。第四阶段：2014年至2019年，人民币汇率缓慢回升。由于受国际贸易和中国经济形势的影响，人民币持续贬值。

图1中，上证指数也经历了大幅的波动，其走势可以大致划分为四个阶段。第一阶段：1991年至2005年，上证指数波动相对稳定，总体呈上升趋势。第二阶段：2005至2008年间，上证指数大幅上涨。其原因是中国经济飞速发展的阶段，股票市場随之繁荣。同时，自2005年4月起，中国进行了股权分置改革，刺激了市场发展。2007年十月，上证指数达到6124点的历史最高位。第三阶段：2008年至2015年，上证指数走势呈现U型，经历了急速下跌，底部大幅震荡和急速上升的一系列过程。2008年，受全球金融危机等内外因素影响，股价大幅下跌，上证指数触碰1664点的低位。2010年至2015年，人民币稳健持续增长，股价持续下跌。同期，人民币保持升值趋势，人民币汇率不断下降，反应外资对于中国经济和资本市场有良好预期。这一时期，股价波动背离国内经济高速发展的基本面。2014年-2015年，股票短期内快速上涨，呈现报复性增长的趋势。第四阶段：2015年至2019年，上证指数走势呈现L型，经历了急速下跌和底部大幅震荡的过程。2015年，股价报复性下跌。同时，由于沪深两市实施了熔断机制，股价大幅下跌。此后的几年内，上证指数持续在3000点上下波动。

（二）汇率变化率和股价变化率统计

根据第三章中的公式，可以计算两个指标的变化率。图2是1991年1月至2019年9月，汇率变化率和股价变化率的走势图。其中，蓝线表示汇率的变化率，黄线表示股价的变化率。

表1是关于汇率变化率和股价变化率的统计量。样本平均值大于0。从1991年1月至2019年9月，汇率的平均变化为正，表明汇率总体呈现上升的趋势。股市的平均月收益率为0.9%，表示股票总体呈现上涨趋势。汇率变化率的方差约为0.023，股价变化率的方差约为0.099。从中可以看出股票市场到波动性高于汇率市场，因此股市的风险相对于汇市较高。汇率变化率的最大值约为0.405，最小值约为-0.034;股价变化率的最大值约为0.657，最小值约为-0.292。

（三）平稳性检验和协整检验

在使用VAR-MGARCH 模型之前，需要对变化率数据进行平稳性检验和协整检验。本文利用KPSS （Kwiatkowski-Phillips-

Schmidt-Shin）方法进行平稳性检验，使用Engle-Granger两步法进行协整检验。

表2是KPSS平稳性检验的结果。在该方法中，如果KPSS统计量大于临界值，则拒绝原序列平稳的假设，序列为非平稳。从表中可以看出，在显著性水平为1%的情况下，汇率和股指的趋势临界值及无趋势临界值皆大于KPSS统计量，因此无法拒绝原序列平稳的假设，序列平稳。

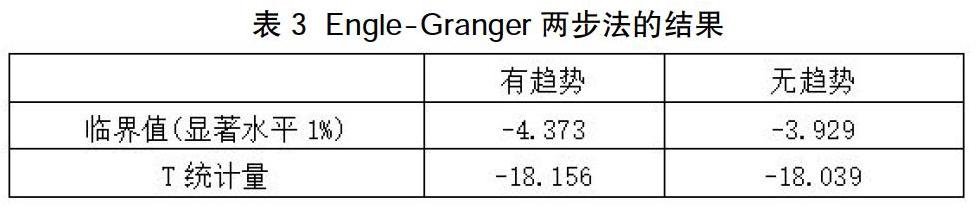
表3是Engle-Granger两步法进行协整检验的结果。在该方法中，若T统计量小于临界值，则表明序列拒绝存在单位根的原假设。从中可以看出，在显著性水平为1%的情况下，T统计量大于临界值，因此表明序列中存在单位根，汇率和股指之间存在协整关系。这一结果表明，汇率和股票之间很有可能存在长期显著的关系。

（四）基于MGARCH-BEKK 模型的波动溢出效应分析

在前面的基础上，为了研究外汇市场和股票市场之间的波动溢出效应，本文使用MGARCH-BEKK模型对变化率进行分析。

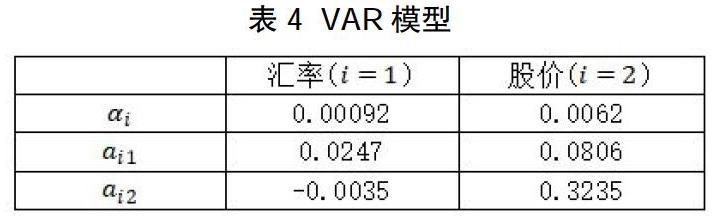
首先，建立变化率的VAR模型，结果如表4所示。

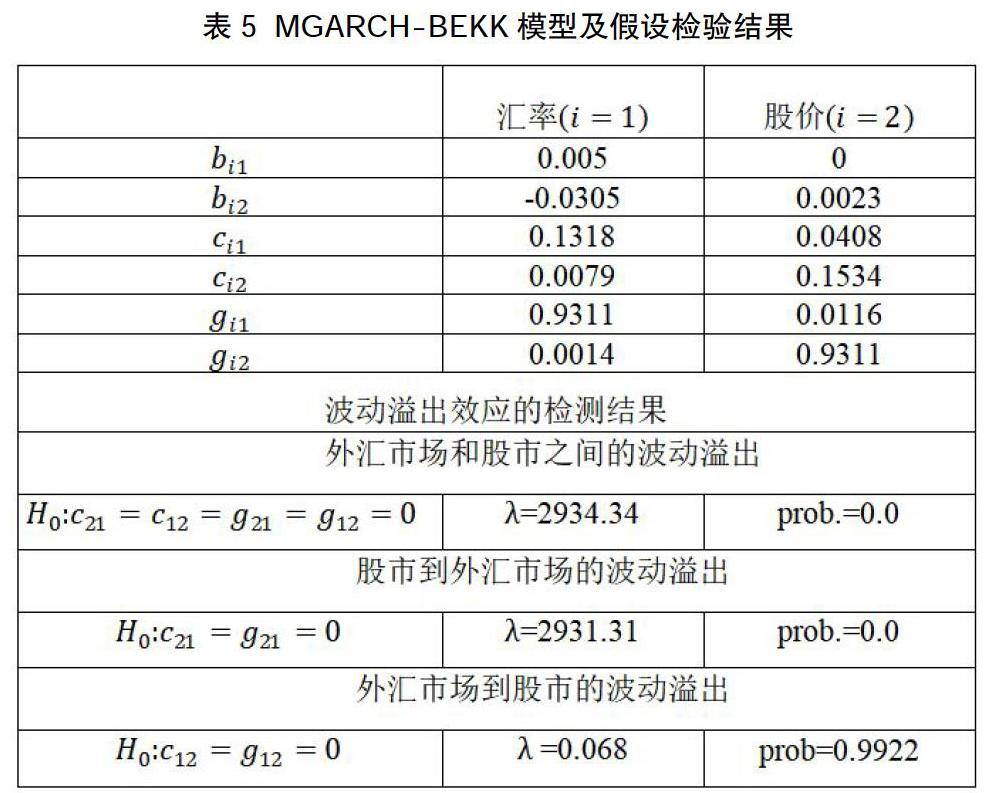
进一步，建立MGARCH-BEKK模型，并进行假设检验，分析结果如表5所示。

本文通过似然比统计量λ来检验外汇和股票市场之间的交叉波动效应。矩阵C和G的原假设是矩阵的非对角元素为零，从结果中看出，由于矩阵C， G的非对角元素不为零，因此拒绝原假设，两者之间存在波动溢出效应。进一步考虑波动溢出的方向。在股市到汇市的波动溢出中，似然比统计量为2931.31，似然比统计量的概率为0，因此拒绝原假设，表示存在从股市到汇市的波动溢出效应。再考虑汇市到股市的波动。似然比统计量为0.068，似然比统计量的概率为0.9922，因此无法拒绝原假设，不存在汇市到股市的波动溢出效应。

研究结果表明，股市和汇市之间存在波动溢出效应。股市到汇市有单向的波动溢出效应，而汇市对于股市没有波动溢出效应。这可能是因为中国的新兴股票市场吸引了外国投资者，导致外国资本可能流入和流出中国股票市场。股价波动加剧时，外国资本流入或流出，买卖人民币进行股票投资，因而导致汇率变化加剧。另一方面，在股票等市场进行权益投资时，市场风险、股票本身的价值以及市场预期等因素的重要性大于汇率成本的重要性，因而汇市对于股市没有波动溢出效应。

五、结论

本文使用了从1991年1月至2019年9月的人民币汇率和上证指数数据，研究了汇率和股价之间的关系。结果显示人民币汇率和中国股价之间存在波动溢出效应。其中，股市对于汇市有单向的波动溢出效应，说明股市的变化和波动会导致人民币汇率波动。同时，汇市对股市不存在波动溢出效应。该研究将有助于金融从业者和其他经济学者更好地理解中国外汇和股票市场，并对汇率和股价的变化做出更准确的预测。

参考文献：

[1]J. D. Hamilton. Time Series Analysis. Princeton University Press， Princeton， 1994.I. S.A. Abdalla， V. Murinde. Exchange rate and stock price interactions in emerging financial markets： Evidence on India， Korea， Pakistan and the Philippines. Applied Financial Economics， vol. 7， no.1， 1997， pp. 25-35.

[2]R. Aggarwal. Exchange rates and stock prices： A study of the U. S. capital markets under floating exchange rates. Akron Business and Economic Review， vol. 12， 1981， pp. 7-12.R. Roll. Industrial structure and the comparative behavior of international stock market indices.？The Journal of Finance， vol.？47， no.1， 1992， pp. 3-41.

[3]H. Zhao. Dynamic relationship between exchange rate and stock price： Evidence from China.？Research in International Business and Finance， vol.？24， no.2， 2010， pp. 103-112.

[4]張兵， 封思贤， 李心丹， 汪慧建. 汇率与股价变动关系： 基于汇改后数据的实证研究. ？经济研究， 第9期， 2008年，  第70-81页.

[5]赵进文， 张敬思. 人民币汇率， 短期国际资本流动与股票价格——基于汇改后数据的再检验. 金融研究， 第1期，  2013年， 第9-23页.

[6]Statsmodels. https：//statsmodels.org

[7]Pandas. https：//pandas.pydata.org

[8]MFE 工具包. https：//kevinsheppard.com/code/matlab/mfe-toolbox

[9]英为财情. https：//cn.investing.com/

[10]网易财经. https：//money.163.com/stock/

[11]D. Kwiatkowski， P.C.B. Phillips， P. Schmidt and Y. Shin. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics， no. 54， 1992， pp. 159-178.

[12]R. F. Engle and C. W. J. Granger. Co-Integration and Error Correction： Representation， Estimation， and Testing. Econometrica， vol. 55， no. 2， 1987， pp. 251-276.