顶爆和拱腰侧爆同时作用下锚固洞室的动态响应
2020-04-14王光勇曹安生林加剑
王光勇,曹安生,余 锐,林加剑
(1.河南理工大学土木工程学院,河南 焦作 454000;2.安徽大学电气工程与自动化学院,安徽 合肥 230601)
钻地弹钻入被攻击目标后再发生爆炸,对武器库、指挥部和避难所等建在地下的重要军事、民用设施形成威胁。近年来,钻地弹频繁出现在战场上,世界各军事强国都在加紧对钻地弹的研究,钻地弹的发展对地下防护工程提出了更高的要求。地下防护工程的安全与否直接关系着战争的成败。我国著名防护工程专家钱七虎院士曾指出[1]:“如果说核弹是锐利的矛,那么防护工程则是坚固的盾”。如何增强地下防护工程抵御钻地弹精确打击的能力,成为目前亟待解决的问题。因此,研究爆炸荷载作用下地下洞室的动力响应,对提升地下防护工程这一“地下钢铁长城”的抗爆能力具有重要的历史和现实意义。
锚杆是一种具有经济有效、施工速度快等特点的支护方式,在地下工程中得到广泛应用。目前国内外学者对锚固洞室在动荷载作用下的动态响应进行了大量的研究。国内方面,顾金才等[2-9]从人防方面通过相似模型试验和数值模拟,从围岩应力、洞壁位移、洞室振动加速度以及破坏形态等方面对地下洞室的抗爆性能进行了研究,并提示了锚固洞室在动载作用下的破坏机理,提出了进一步提高锚固洞室抗爆能力的技术措施。为了揭示锚杆对地下洞室抗爆效果的影响,单仁亮[10]、王正义[11]、吴拥政[12]等从民用方面应用模型试验、数值分析等方法研究了锚固巷道在动载作用下的动态响应,并对锚固巷道的损伤破坏机制进行揭示,探讨了锚杆受力机理,给出了相应破坏类型及判据。国外的相关研究主要集中在民用方面,Rajmeny等[13]通过试验研究了临近采场高应力区洞室在爆破动载作用下围岩破坏现象及预测方法。在露天开采爆破时,Singh[14]指出爆破围岩振动幅度值是决定洞室围岩产生裂缝和剥离破坏程度的主要因素。Hagedorn[15]采用UDEC程序评估了喷锚支护洞室在两次相继冲击作用后的稳定性。Yugo等[16]通过现场监测发现相邻锚固巷道受连续爆破荷载作用时会发生破坏,并提出相应的抗爆措施。Deng等[17]研究了在爆破动载作用下含节理圆形巷道的破坏程度及形式,并得出锚杆能够有效地提高巷道抗动载能力。虽然国内外已经在地下锚固洞室爆炸动态响应方面取得很多成果,但成果大多关于单爆源作用下洞室的动态响应,很少有对多爆源同时作用下的洞室进行研究。实际战争中,地下防护工程可能面临不同位置爆源同时爆炸的影响。故本研究基于相似模型试验,通过数值分析,对地下洞室在拱顶、拱腰侧两处集中装药爆源同时作用下的应力波传播、裂纹形成及洞壁围岩位移分布开展研究,从而进一步丰富地下锚固洞室抗爆设计。
1 数值计算
1.1 几何模型
数值计算模型取自室内试验模型[9],为方便计算,模型经过二维处理,模型宽、高、厚分别取240、230、4 cm,洞室跨度取60 cm。按照试验模型中拱顶和拱腰侧爆源相同位置,在数值计算模型拱顶和拱腰侧同时布置质量为50 g的TNT炸药,如图1所示。洞室采用锚杆间、排距均为4 cm,长24 cm的单排全长黏结式锚杆锚固。为了测量围岩的压应力,在计算模型上布置9个围岩应力测点,即在拱顶爆源下20、40和60 cm处布置测点P1、P2和P3,在相邻两爆源的中点与洞室拱部圆心的连线上布置间距为20 cm的P4、P5和P63个测点,P7、P8和P9为拱腰侧爆源在洞室径向的3个测点。为了监测洞壁围岩位移,在洞壁的周围布置编号为①~⑫的监测点,具体见图1。

图1 数值计算模型(单位: cm)Fig.1 Model of numerical analysis (Unit: cm)
1.2 材料模型及参数
为模拟爆炸应力波在岩体中的传播,将计算模型上表面设为自由边界,左右侧面和下表面设置为无反射边界,前、后两个面设置为水平位移为零边界,不计岩体自重的影响。岩体、炸药设为3DSolid164单元,锚杆设为Beam161单元,采用拉格朗日网格建模。选用材料编号为78,定义方式为*MAT_SOIL_CONCRETE的混凝土本构模型来模拟岩体。当岩体单元的受拉强度超过其抗拉强度时,根据von Mises破坏准则,岩体单元失效,删除失效单元,从而形成裂纹,以描述岩体破坏。数值分析中采用高能炸药材料模型*MAT_HIGH_EXPLOSIVE_BURN 和*EOS-JWL 状态方程来描述炸药。爆轰过程中压力和比容的关系为

式中:A、B、R1、R2、ω为材料常数,p为压力,V为相对体积,E0为初始比内能。对于锚杆,用各向同性弹塑性模型*MAT_PLASTIC_KINEMATIC作为本构模型。岩体、炸药、锚杆的材料密度分别为1.70、1.63和2.72 g/cm3,其他材料参数见表1[18],其中G、K为岩体材料的剪切模量、体积弹性模量,pCJ为炸药爆轰压力,DH为炸药的爆速,E、µ为锚杆材料的弹性模量、泊松比。

表1 数值计算模型的材料参数[18]Table 1 Material parameters for the analysis model[18]
2 数值计算结果分析
2.1 试验结果和数值模拟结果对比分析
为了验证计算模型中材料参数的可用性,将模拟中测点的压应力时程曲线与试验中同位置的压应力时程曲线进行对比,由于试验只做了拱顶爆炸,所以只对拱顶爆源作用下的模拟和试验结果进行对比分析。图2为拱顶单爆源作用下P1、P2和P3测点的计算模型进行炸药当量折算后与试验实测压应力时程曲线的对比。由图2可以得到:模拟和试验的压应力时程曲线形态比较相似,都是先迅速上升达到峰值,然后下降,最后达到平衡,但数值分析的应力波明显比试验中的应力波超前到达各测点,作用时间也较试验短。对比相同位置的压应力峰值发现:P1的试验压应力峰值大于数值分析值,P2的试验压应力峰值与数值分析结果比较接近,而P3的试验压应力峰值小于数值分析结果,因此试验中应力波强度明显比数值分析中应力波强度衰减得快。产生以上现象的主要原因是数值计算模型把岩体理想化了,忽略了岩体中的不连续结构面对应力波传播的影响,而试验中的岩体是分层夯实形成,会有类似岩体中节理面的存在,此节理面能增加应力波能量的耗散,从而导致数值分析的应力波强度衰减得更慢,传播得更快。以上结果充分说明数值分析结果是可信的。

图2 模拟与实验岩体单元压应力时程曲线对比Fig.2 Comparison of pressure curves of rock elements between numerical and experimental results
2.2 应力波传播及作用过程分析
图3显示了在拱顶和拱腰侧两处爆源同时爆炸作用下锚固洞室围岩中应力波的传播过程,图中正值表示岩体受压,负值表示受拉。集中装药爆源爆炸时瞬间释放出巨大的能量,在爆生气体高温高压的作用下,两爆源附近的岩体被极度压碎破坏形成爆腔,各个爆源爆炸产生的压应力波以圆形向周围传播,压应力波波形曲线是先增加后减小,见图3(a),这与集中装药爆炸理论比较吻合。当应力波作用到0.3 ms时,两个爆源产生的压应力波开始相遇,此时发生相遇的是峰值前上升阶段的波,但是从图3(b)中可以看出应力相互作用区域的应力波的强度是最大的,明显高于单爆源产生的压应力波峰值,达到11.6 MPa,说明两个压应力波相互作用会形成更强的压应力波。随着应力波继续向前传播,两个爆源产生的压应力波相遇区域一直是同时刻应力波最强的地方,并且应力波最强区域越来越扁平,如图3(c)和图3(d)所示,与此同时,当应力波向上传播到地表自由面时,会由于压应力波反射形成拉伸波而出现“层裂”现象,形成一定的拉伸裂纹。当应力波传播到0.7 ms时,应力波向下已经传播到地下锚固洞室,虽然前面压应力波已经反射成拉伸波,但由于应力是先上升,所以反射拉伸波与后面的压应力波作用后还是呈现受压状态,直到应力波传播到0.8 ms时应力波作用呈现拉应力状态,此时拉应力大于锚固围岩动态抗拉强度,形成局部裂纹。随着应力波传播时间推移,地表自由面下面的裂纹逐渐沿着两爆源的中点与洞室拱部圆心的连线向下延伸,一直延伸到爆源以下,并且埋深越大,裂纹的分布越窄;锚固洞室附近的裂纹随着应力波的传播,除了在锚固洞室自由面附近形成小孔洞,由于锚杆的加固作用使锚固区锚杆之间形成一定数量的劈裂裂纹,当反射拉应力波继续向前传播到非锚固区,产生的劈裂裂纹越来越少,但横向裂纹越来越多,逐渐沿着两爆源的中点与洞室拱部圆心的连线向上延伸,与此同时,地表自由面反射的拉伸波和锚固洞室反射的拉伸波相互作用,拉应力得到加强,从而在爆源两侧附近形成“八”字形的裂纹区,并且图中左边裂纹比右边裂纹更粗、更广,这是由于左边的应力波叠加处的传播路径比右边的短,应力波能量损耗小,叠加处的拉应力较右边大。

图3 应力波传播过程Fig.3 Process of stress wave propagation
上面主要是从定性方面分析爆炸应力波的传播规律,在不同爆炸情况下的具体应力波强度变化规律还是不清楚,为了更好地了解锚固洞室在爆炸荷载作用下的破坏情况,有必要对锚固洞室附近关键部位的应力波强度规律进行分析,从而为进一步提高锚固洞室的抗爆能力提供理论依据。单爆源下(顶爆或拱腰侧爆)P1~P9压应力时程曲线如图4所示。其中P1、P2、P3是在顶爆作用下的压应力时程曲线,P7、P8、P9是在拱腰侧爆作用下的压应力时程曲线,由于顶爆和拱腰侧爆中相同位置的P4、P5、P6曲线一样,P4、P5、P6为两者中任一单爆源条件下的压应力时程曲线。图5是拱顶和拱腰侧爆源同时起爆时P1~P9的压应力时程曲线。对比分析图4和图5可以得到:单爆源作用下的压应力时程曲线和峰值衰减规律与实际爆炸规律比较相似,每条时程曲线都是由上升和下降两个阶段组成,离爆源越近的点越先起跳,离爆源越远的点的压应力峰值越小,其中P1、P2、P3和P7、P8、P9测点对应的压应力峰值比较接近,而由于爆心距较大,P4、P5、P6测点的压应力峰值相对小一点;在顶爆和拱腰侧爆同时起爆作用下,P1、P2、P7、P8由于受相邻爆炸的影响在应力波下降阶段再次形成一个波峰,曲线由单爆源作用下的单波峰变成了双波峰,双爆源作用下P3和P9的压应力峰值比单爆源作用下大,甚至比双爆源作用下P2和P8的压应力峰值大,并且双爆源普遍比单爆源作用下应力波作用时间要短;在双爆源作用下,P1、P2、P3和P7、P8、P9的压应力峰值仍然比较相近,但P4、P5、P6的压应力峰值明显比它们相应位置要大,分别比P1、P2、P3大 16.4%、70.6%、45.3%,比P7、P8、P9大 28.0%、69.8%、42.4%。P4、P5、P6压应力峰值明显比单爆源作用下大得多,分别是单爆源作用下压应力峰值的177.2%、195.4%、235.9%。

图4 单爆源作用下锚固洞室岩体单元压应力时程曲线Fig.4 Time history curve of compressive stress of rock elements from anchorage chamber under single explosion

图5 拱顶和拱腰侧爆源同时起爆锚固洞室岩体单元压应力时程曲线Fig.5 Time history curve of compressive stress of rock elements from anchorage chamber under explosion load from top and side of arch
2.3 爆炸荷载作用下岩体裂纹分析
待裂纹发展稳定后,取拱顶和拱腰侧单爆源和两爆源同时作用下的锚固洞室裂纹分布情况进行对比分析,如图6所示。图6中包括单爆源作用下锚固洞室的裂纹分布及双爆源作用下毛洞和锚固洞室的裂纹分布,从4种情况下的裂纹分布可以知道:从作用机理上分,所有的裂纹主要包括由于“层裂”在地表自由面下面和洞室自由面上面区域产生的裂纹以及由于反射拉伸波相遇产生的“八”字形裂纹;在双爆源作用下,由于锚杆的作用,使地表自由面下的破坏深度变浅,地下洞室自由面上面区域裂纹由毛洞的横向裂纹变成锚固洞室的径向劈裂和横向裂纹,并且裂纹变得更细;双爆源作用下锚固洞室的裂纹并不是两个单爆源作用下裂纹叠加,双爆源作用下锚固区的裂纹主要分布在两爆源的中点与洞室拱部圆心的连线上,比单爆源作用下锚固区裂纹更窄,但宽,锚固区与非锚固区之间的裂纹明显比单爆源作用下分布得更广、更宽,双爆源作用下地表自由面下的破坏明显比单爆源作用下深,一旦两爆炸源的威力足够大,会在中点与洞室拱部圆心的连线方向形成贯通,从而导致锚固洞室破坏。
2.4 爆炸荷载作用下锚固洞室动态位移分析
洞壁位移能够反映洞室的破坏特征,为了分析单爆源和两爆源洞壁位移的特点,将顶爆、拱腰侧爆和两爆源同时爆炸时的锚固洞壁周围12个监测点(见图1)的位移峰值绘制成图7,其中沿洞室径向的直线长度代表该监测点位移的大小。由图7可知:由于应力波的相互作用,双爆源作用下的位移峰值分布与单爆源作用下的位移峰值分布明显不同,在单爆源作用下离爆源最近的洞壁位移峰值最大,并由此向两侧逐渐减小,而双爆源作用下两爆源中间洞室径向上的②号监测点的位移峰值最大,向两侧逐渐减弱,锚固洞室右侧位移峰值明显比左侧位移峰值大,并且其最大位移峰值比两个爆源单独作用下的位移之和还大22.8%,这也和前面的压应力分析结果相吻合。
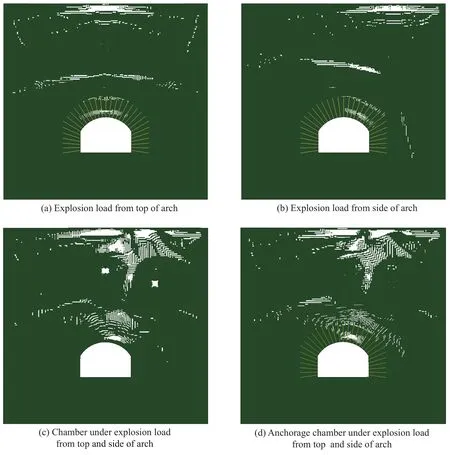
图6 围岩裂纹分布情况Fig.6 Crack distributions of surrounding rock

图7 洞壁位移(单位: mm)Fig.7 Displacement of the cavern (Unit: mm)
3 结 论
(1)两个集中药包同时起爆后,爆源附近的岩体在爆生气体高温高压作用下,被极度压碎破坏形成爆腔,其应力波分别以爆源为中心以圆形(球面波)向周围岩体传播,在两应力波相遇处,压应力强度增加且明显大于周围岩体。
(2)当应力波传至模型上自由表面、洞室自由面时,反射后形成拉伸波,当拉应力大于岩体动态抗拉强度时,岩体发生“层裂”现象,出现多层裂纹,并且两个自由面上反射产生的裂纹在两爆源的中点与洞室拱部圆心的连线上延伸,最终可能形成贯通。当两拉伸波在爆源下方不远处相遇并叠加时,在波阵面交汇处产生“八”字形锥形裂纹面。
(3)锚杆的锚固作用使锚固区的裂纹分布范围变小,且能够抑制裂纹横向发展,使锚固区围岩沿锚杆产生径向劈裂裂纹。
(4)两爆源中间的洞壁位移峰值最大,易产生破坏,从此处向两侧洞壁的位移峰值逐渐减小,锚固洞室右侧位移峰值明显比左侧位移峰值大。
