金属材料在极高应变率下的力学性能测试
2020-04-14王子豪文鹤鸣
王子豪,郑 航,文鹤鸣
(中国科学技术大学中科院材料力学行为和设计重点实验室,安徽 合肥 230027)
金属材料因具有良好的延展性和性价比,在军事和民用工程领域中得到了广泛的应用。在爆炸和冲击载荷下,金属材料的响应和破坏伴随着大变形、高应变率和高温。金属材料在较高应变率下会表现出增强效应,在较高温度下会表现出软化效应。
Johnson等[1]提出了一个预测金属材料应变率(增强)效应的表达式,该表达式因形式简单、参数少得到广泛应用。周琳等[2]对该表达式的精确性进行评估后发现:当应变率大于103s−1时,金属材料的强度明显增强,Johnson等[1]提出的应变率效应表达式并不能反映这种增加趋势。Steinberg等[3]提出了一个当应变率大于105s−1时可以较好地反映材料动态力学行为的本构模型,将模型中剪切模量和屈服强度表示为等效塑性应变、压力和温度的函数,并认为在高应变率条件下可以忽略应变率对材料强度的影响。
分离式霍普金森拉杆(SHTB)和霍普金森压杆(SHPB)实验是测试金属材料在中低应变率(小于104s−1)下力学响应最常用的测试技术,而材料在极高应变率下的力学行为只能通过气炮实验进行研究。Asay等[4-5]和Chhabildas等[6]发展了一种测定材料在冲击压缩条件下剪切强度的方法 (AC法),通过对预冲击材料进行再加载或卸载到其上、下屈服面,获得材料在预冲击状态下的强度。
本研究通过在二级轻气炮上进行平板撞击实验,利用AC法对实验数据进行分析,测定93钨合金和921A钢在极高应变率下的动态屈服强度,并结合文献[7-9]所报道的中低应变率下的相关结果,给出93钨合金和921A钢在应变率为10−4~106s−1范围内的动态屈服强度,为金属材料动态本构模型的研究提供关键参考依据。
1 实验基本原理
冲击波作用下材料的高压声速就是冲击波后稀疏波的传播速度。目前用于高压声速测量的技术主要是加窗激光干涉测速技术,如DPS、DISAR。利用加窗激光干涉测速技术测量样品/窗口界面的粒子速度剖面从而得到声速的原理如图1所示。为简单起见,假定为对称碰撞并形成单一冲击波结构。当飞片与样品发生碰撞时(时间t=t0),飞片中产生左行冲击波,同时在样品中产生右行冲击波。当样品中的冲击波到达样品窗口界面时(A点,t=tA),界面的粒子速度突跃为ul=uA;当飞片中的左行冲击波到达后表面时(B点),将反射一中心卸载稀疏波,中心卸载稀疏波包括传播速度较快的弹性波和相对较慢的塑性波;当传播速度较快的弹性卸载波到达界面时(C点,t=tC,ul=uC),使界面粒子速度下降,在速度剖面上形成第1个拐点;当塑性卸载波到达界面时(D点,t=tD,ul=uD),界面粒子速度再次突变,在速度剖面上形成第2个拐点。由图1(b)所示的几何关系可知,在任意时刻tR,与速度剖面上R点(界面速度为uR)对应的拉格朗日声速CR可表示为[10-11]

式中:D为样品中的冲击波速度,hs为样品厚度,hf为飞片厚度。

图1 加窗激光干涉测速技术测量声速示意图(实线表示冲击波,虚线表示追赶稀疏波)Fig.1 Schematic diagram of the measurement of sound speed by windowed laser interferometry(Solid line indicates shock wave and broken line designates rarefaction wave)
在测得拉格朗日声速的基础上,根据特征线上的相容关系可以进一步得到沿着卸载过程的密度、应力、应变和比容等随时间的变化关系,即卸载路径。由此可以得到沿着卸载路径的欧拉声速

式中:ρ0为样品的初始密度,ρ为样品瞬时密度。图1中弹性卸载波(C点)对应的声速称为Hugoniot状态纵波声速cl,对应的体波声速cb需要通过将塑性段声速(DR段)线性外沿至Hugoniot状态得到。在此基础上可以计算得到动态剪切模量

由于93钨合金和921A钢的阻抗比LiF窗口的阻抗高,如果采用图1所示的对称碰撞方式,则样品中冲击波在样品/窗口界面反射的稀疏波(图1(a)中A点)将与后续的追赶稀疏波相互作用,从而影响声速测量精度。为此,采用反向碰撞方法[12](以待测样品为飞片)进行冲击实验,减弱冲击波在样品/窗口界面反射稀疏波的影响,从而提高声速测量精度。
反向碰撞实验原理如图2所示。根据波系传播可以得到与速度剖面上任意速度uR对应的拉格朗日声速[11-12]

屈服强度的测量则可以采用双屈服面方法[5,11]。在该方法中,除了进行上述冲击加载-卸载波剖面测量外,还需进行冲击加载-再加载波剖面测量,并获得卸载和再加载过程声速及工程应变,如图3所示,uw表示窗口的粒子速度,u表示样品-窗口界面的粒子速度。其中沿卸载路径

沿再加载路径

式中:Cl为拉格朗日纵波波速;Cb为拉格朗日体波波速;τ0为Hugoniot状态剪应力;τc为临界剪切应力,即剪切强度;e为工程应变。
积分上限1表示下屈服面位置,积分上限2表示上屈服面位置。由式(5)和式(6)可以得到屈服强度


图2 反向碰撞方法测量声速原理图(实线表示冲击波,虚线表示追赶稀疏波)Fig.2 Schematic diagram of the measurement of sound speed by reverse impact(Solid line indicates shock wave and broken line designates rarefaction wave)

图3 双屈服面强度测量方法Fig.3 Method for measuring technique to measure dynamic yield strength
2 93钨合金和921A钢强度实验
根据图3所示的实验原理,利用反碰法设计实验。实验在发射管口径为30 mm的二级轻气炮上进行,测量了冲击加载-卸载波剖面的光学信号。93钨合金进行了2发实验,921A钢进行了3发实验。样品撞击窗口前的飞行速度vi由磁测速装置测量,典型的磁测速信号如图4所示。利用DPS测量LiF窗口界面的光学信号,典型的DPS光学信号如图5所示。

图4 典型磁测速信号Fig.4 Typical magnetic speed signals
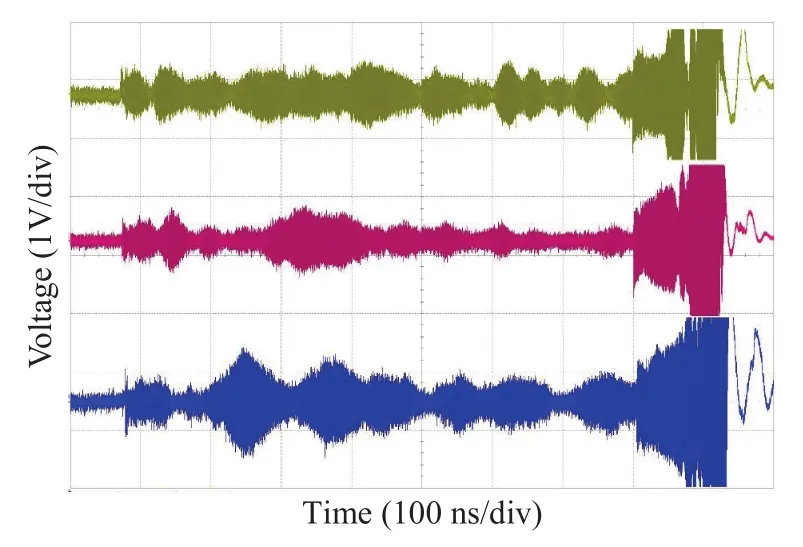
图5 典型DPS光学信号Fig.5 Typical DPS optical signals
对于从DPS得到的多普勒干涉信号,需经过下述步骤处理得到一维应力条件下的动态屈服强度和平均应变率。
(1)由DPS光学信号求得样品-窗口界面的粒子速度[13]。样品-窗口界面的粒子速度u(t)为

式中:λ为波长;f(t)为反射干涉光的多普勒频移;∆v/v0为修正因子,修正窗口材料在高压下折射率的变化。处理后得到的加载、卸载波历史如图6所示,其中vi为样品撞击窗口的飞行速度。

图6 93钨合金和921A钢加载和卸载速度-时间历史Fig.6 Loading and unloading velocity-time histories for 93 tungsten alloy and 921A steel
(2)采用阻抗匹配法求得冲击后样品材料的粒子速度。由于窗口材料的冲击波阻抗与样品材料的冲击波阻抗并不相同,所以测得的样品-窗口界面的粒子速度是入射波在样品/窗口界面反射后的粒子速度。需要用阻抗匹配法求出反射后样品窗口的冲击压力(pH)。

式中:下标“w”表示窗口材料,窗口材料为LiF,冲击波速度D和粒子速度u的关系为D= 5.148 +1.353u(km/s)[14];下标“s”表示样品材料,分别为93钨合金和921A钢。93钨合金密度为17.44 g/cm3,冲击波速度D和粒子速度u的关系为D= 4.007 + 1.276u(km/s)[14];921A钢密度为7.83 g/cm3,冲击波速度D和粒子速度u的关系为D= 3.694 + 1.706u(km/s)(由本研究中921A钢实验结果拟合得到)。部分实验阻抗匹配如图7所示。

图7 93钨合金和921A钢阻抗匹配Fig.7 Impedance-match for 93 tungsten alloy and 921A steel
(3)应用式(4)可以得出冲击加载-卸载实验速度剖面处的拉格朗日声速C随粒子速度u的变化关系,如图8所示。黑色线起始处的声速为Hugoniot状态纵波声速,体波声速则通过将塑性段声速线性外推得到(红色线所示)。利用式(3)和式(2)可以计算处于Hugoniot状态材料的剪切模量G,再应用式(5)对声速-粒子速度数据进行计算,得到材料卸载过程的 τc+τ0。

图8 93钨合金和921A钢的声速-粒子速度拉格朗日分析Fig.8 Lagrangian analysis of sound speed-particle velocity for 93 tungsten alloy and 921A steel
(4)利用Steinberg本构模型,假设YH/G为常数,估计动态屈服强度。由于缺乏再加载实验,因此不能直接得到Hugoniot状态下的剪切强度τ0。一般来说,冲击Hugoniot状态剪应力 0 ≤ τ0≤ τc,因此可以得到动态屈服强度 τc+τ0≤YH≤ 2(τc+τ0)。动态屈服强度(YH)与一维应力条件下的动态屈服强度(σd)的关系可以表示为

式中:ν为泊松比。93钨合金的准静态屈服强度为0.62 GPa[7],准静态剪切模量为91.81 GPa[15];921A钢的准静态屈服强度为0.70 GPa[8], 由于YH要满足 τc+τ0≤YH≤ 2(τc+τ0)的要求,其准静态剪切模量只能在63.0~66.0 GPa范围内。
(5)利用冲击波速和样品厚度估计整个加载过程的平均应变率。加载过程的应变可以表示为ε=Δu/C0, Δu为界面粒子速度的变化量,C0为纵波波速。在样品产生卸载波之前的时间t=hs/C0,hs为样品厚度。最终处理得到的实验结果见表1,其中:vi为撞击速度,pH为冲击压力,σd为一维应力条件下的动态屈服强度。
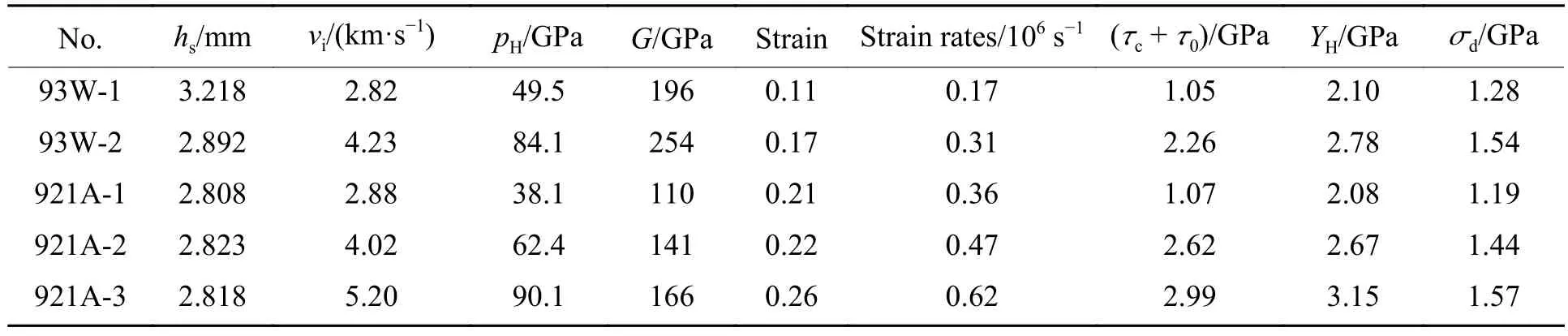
表1 93钨合金和921A钢的实验结果Table 1 Test results for 93 tungsten alloy and 921A steel
3 讨 论
结合陈青山等[7]得到的93钨合金实验数据和朱锡[8]、张林等[9]得到的921A钢的实验数据,分析93钨合金和921A钢的屈服强度随应变率的变化关系,分别如图9、图10所示。其中,DIF为动态增强因子,是动态屈服强度与准静态屈服强度的比值。对93钨合金而言,从图9可以发现,在应变率小于1 s−1时动态增强因子(动态屈服强度)随应变率的增加而增加,但增强效应并不明显;当应变率大于1 s−1,随着应变率的增加,动态增强因子会明显增加;当应变率超过104s−1时,动态增强因子随应变率的增加变化缓慢;随着应变率的进一步提高,动态增强因子几乎接近于一个常数。对921A钢而言,从图10可以发现:当应变率小于1 000 s−1时,921钢的动态屈服强度随应变率几乎没有变化;当应变率大于约1 000 s−1时,921A钢的动态屈服强度随应变率增大而迅速增加;当应变率大约为3 000 s−1时,其动态屈服强度约为静态屈服强度的2.1倍;其后动态屈服强度随着应变率的增加变化缓慢。这里需要强调的是,本研究中的921A钢的平板撞击实验数据(图10中圆圈所示)有点分散,与文献[9]报道的实验结果(图10中上三角所示)类似,但动态增强因子的平均值保持在2.1左右,几乎是常数。
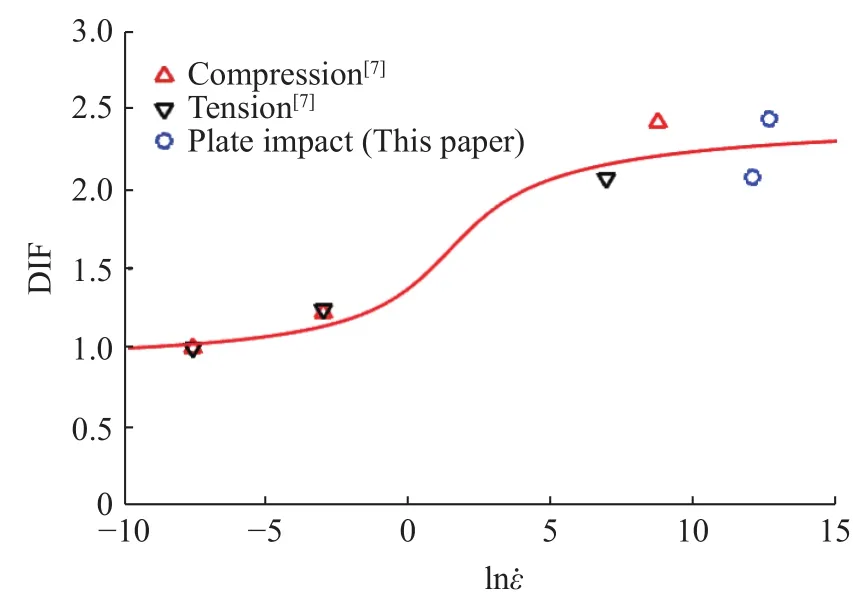
图9 93钨合金的DIF随应变率的变化Fig.9 Variation of DIF with strain rate for 93 tungsten alloy

图10 921A钢的DIF随应变率的变化Fig.10 Variation of DIF with strain rate for 921A steel
4 结 论
通过二级轻气炮进行了平板撞击实验,得到了93钨合金和921A钢冲击加载-卸载波剖面的粒子速度,通过分析处理得到了93钨合金和921A钢在极高应变率下的动态屈服强度,并结合文献中报道的中低应变率下的实验结果得到了两种材料在较大应变率(10−4~106s−1)范围屈服强度随应变率的变化规律,主要结论如下。
(1) 93 钨合金在应变率(冲击压力)为 1.7 × 105s−1(49.5 GPa)和 3.1 × 105s−1(84.1 GPa)下的动态屈服强度分别为 2.10 GPa 和 2.78 GPa;921A 钢在应变率(冲击压力)为 3.6 × 105s−1(38.1 GPa)、4.7 × 105s−1(62.4 GPa)和 6.2 × 105s−1(90.1 GPa)下的动态屈服强度分别为 2.08 、2.67 和 3.15 GPa。
(2) 93钨合金基本上是应变率敏感材料,屈服强度随着应变率的增加而增加。当应变率大于1 s−1,随着应变率的增加,动态屈服强度增加明显;当应变率超过104s−1时,动态屈服强度随应变率的增加变化缓慢;随着应变率的进一步提高,动态屈服强度几乎接近于常数。
(3) 921A钢在应变率小于1 000 s−1时,动态屈服强度随应变率的增加几乎没有变化;当应变率大于1 000 s−1时,动态屈服强度会随应变率的增大而迅速增加;而当应变率大约为3 000 s−1时,其动态屈服强度约为静态屈服强度的2.1倍;其后,动态屈服强度随着应变率的增加变化缓慢。
