小展弦比飞翼标模FL-2风洞跨声速开孔壁干扰特性修正研究
2016-04-06李鸿岩王祥云杨希明王世红
李鸿岩,王祥云,杨希明,王世红
(中国航空工业空气动力研究院高速高雷诺数气动力航空科技重点实验室,辽宁沈阳 110034)
小展弦比飞翼标模FL-2风洞跨声速开孔壁干扰特性修正研究
李鸿岩*,王祥云,杨希明,王世红
(中国航空工业空气动力研究院高速高雷诺数气动力航空科技重点实验室,辽宁沈阳 110034)
为了满足现代风洞试验精细化要求,提高风洞试验数据精准度,开展跨声速开孔壁洞壁干扰修正方法研究。本文利用实测壁压信息构造开孔壁边界条件,通过求解N-S方程,模拟试验模型在风洞中的绕流场,建立基于壁压信息的跨声速洞壁干扰非线性修正方法。不同于线性修正方法,本方法可用于各种复杂外形飞行器的亚、跨声速开孔壁洞壁干扰修正,结合小展弦比飞翼标模风洞试验数据,对其在FL-2风洞试验数据开展洞壁干扰特性研究。洞壁干扰修正结果表明,洞壁干扰量随马赫数变化呈增长趋势,Ma=1.0左右达最大,经过修正的FL-2风洞的跨声速试验结果,与FL-26风洞近似无干扰试验结果吻合良好。
壁压;洞壁干扰;飞翼标模;非线性
0 引 言
当今飞行器的研制与发展仍然离不开准确的风洞试验数据。由于高速风洞试验段尺寸的限制,洞壁干扰是影响试验数据准确性的重要因素,特别是在跨声速模型试验时,洞壁干扰更加突出。跨声速风洞洞壁干扰是实验空气动力学中众所周知的难题之一,其困难主要在于在跨声速范围内,流动比较复杂。洞壁干扰研究工作一般从两方面进行:一方面是采用一些特殊的风洞试验段壁板的方法或采用减小模型尺寸、增大风洞尺寸的方法来设法减弱洞壁干扰效应;另一方面是设法对已存在的洞壁干扰效应进行修正[1-4]。
实践表明,一般情况下用上述各种改进壁板和减小模型尺寸的方法都不可能完全消除亚、跨声速试验的洞壁干扰效应。对于要求数据准度较高的亚、跨声速试验,还应对残存的洞壁干扰效应进行修正。洞壁干扰是风洞试验的固有问题,相关的研究工作也从未停止过,世界各国利用很多方法研究过洞壁干扰修正问题,如试验法、经验类推法、壁压信息法和数值计算法等[5-7],由于受开孔壁穿流特性影响,增大了开孔壁数值边界条件的复杂性,因此跨声速洞壁干扰修正一直是各国风洞机构的研究热点和难点。
随着试验精细化程度的提高,测量的精度要求是小于1个阻力单位(0.0001),因此如何消除洞壁干扰影响是关键。国内外公开可查的洞壁干扰修正方法,大都是基于线化速势方程[8]。由于方程的线性特征,有一定的使用限制,就像常说的那样,这些方法很难应用到近声速和有气流分离的情况。
随着基于Navier-Stokes方程的CFD方法发展,洞壁干扰研究方法开始逐步向非线性修正方法过渡[913]。由于受开孔壁的壁板形式影响,使得全流场的网格构建工作量太大,计算成本高,耗时过长。开孔壁数值边界条件的构造,是基于CFD方法的非线性洞壁修正的难点所在。因此构建一种广泛适用于跨声速孔壁风洞壁板的简化数值模型是首先要解决的问题。壁压信息作为代表开孔壁流动特性的典型参数,通过消除壁压数据不规则性、流场的不均匀性和支架的影响等一系列措施,可获得较为准确的壁压信息。通过壁压信息构造开孔壁边界条件,为跨声速开孔壁洞壁干扰非线性修正方法指明方向。
本文尝试以数学模型化的开孔壁为研究对象,对于亚跨声速风洞的开孔壁流动尝试着建立更合理的基于壁压信息的非线性修正方法,研究小展弦比飞翼标模的FL-2风洞跨声速洞壁干扰特性。结合FL-2风洞的实际情况,对壁压数据进行合理处理。采用实测壁压构造开孔壁边界条件,选择N-S方程作为流场主控方程,通过对比带和不带洞壁两种计算结果,得到洞壁干扰影响量。计算结果表明,本文可以很好地模拟跨声速开孔壁影响,可用于复杂外形飞行器的跨声速洞壁干扰修正,具有较好的工程应用前景。
1 洞壁干扰修正方法
本文所采用的洞壁干扰修正计算的研究方法是:分别计算模型在风洞中试验状态(带洞壁边界条件)及相应自由流飞行状态的全机气动力及流场情况,相应状态下计算结果的差值为该状态下洞壁对试验结果的干扰量,而试验结果加上计算获得的干扰量即为洞壁干扰修正值。以纵向洞壁干扰修正计算为例,式(1)分别给出压力系数、升力系数、阻力系数、俯仰力矩系数的洞壁干扰量计算公式及修正公式。
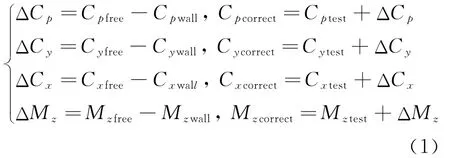
式中的下标“wall”、“free”、“test”和“correct”分别表示带洞壁边界计算结果、自由流计算结果、试验值和修正值。在模型带洞壁和自由流计算中,均采用相同的数值求解方法;为减小网格拓扑形式和数量对计算结果的影响,在风洞流场计算区域内保证相同的计算网格形式,进一步提高计算精度。
2 数值方法
2.1 流动控制方程和计算方法
应用有限体积法对复杂外形绕流流场进行数值模拟,控制方程采用雷诺平均的N-S方程组,其三维Navier-Stokes方程积分形式为:
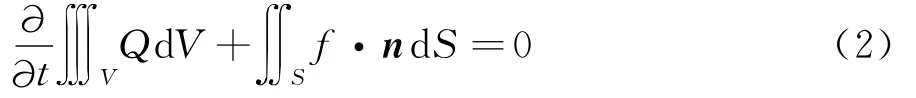
其中,V为控制体体积;Q为矢量形式的守恒变量;S为控制体表面积;f为通过控制体体表面的净通量,包含黏性通量项和无黏通量项;n为控制体表面的单位外方向矢量。
无黏通量计算采用二阶精度的MUSCL-Roe格式,黏性通量计算采用二阶精度中心差分格式离散。本文采用SA湍流模型进行全湍流计算。时间推进采用隐私近似因子分解(AF)方法,推进到定常状态得到流场的定常解。
2.2 边界条件
(1)无滑移边界条件
无滑移边界条件又称黏性壁面边界条件,壁面处法向速度和切向速度均为零,即u=v=w=0。(2)开孔壁边界条件
本边界条件使用风洞实测壁压作为输入条件,额外的流动变量需要自行构造。构造方法及过程为法向速度由一维黎曼不变量确定,两个切向速度由内场外插得到,压强由实测壁压得到,密度由理想气体公式得到,其余变量由等熵关系式获得。当来流马赫数较高,洞壁附近有激波存在时,该边界条件同样适用。需要说明的是,由于试验测量的壁压为离散点且数量有限,实际计算时需要将其插值到开孔壁计算边界网格处,壁压数据处理方法详见下文4.2节。
(3)远场边界条件
对于超声速流动,流入值取自由来流值,流出值由场内外插;对于亚声速及跨声速流动,采用Riemann不变量处理。根据特征线理论,沿特征线各种物理量满足Riemann不变量关系式。根据每一特征值的正负,合理选择远场边界的内、外两侧的状态变量,可唯一确定一组特征变量,利用这些特征变量可计算远场边界网格单元面上的法向数值通量。
3 NACA0012算例验证
为验证上述方法的可行性,基于NACA0012翼型的法宇航S3风洞二维测压试验数据[14]开展洞壁干扰计算研究。对带洞壁和自由流计算模型分别进行了数值模拟计算,并与风洞试验结果进行对比。图1给出了不同工况下有无洞壁计算结果与试验结果的对比曲线。由图1可见带开孔壁边界条件计算的压力分布及激波位置与试验结果吻合较好。洞壁干扰对翼面压力分布影响明显。

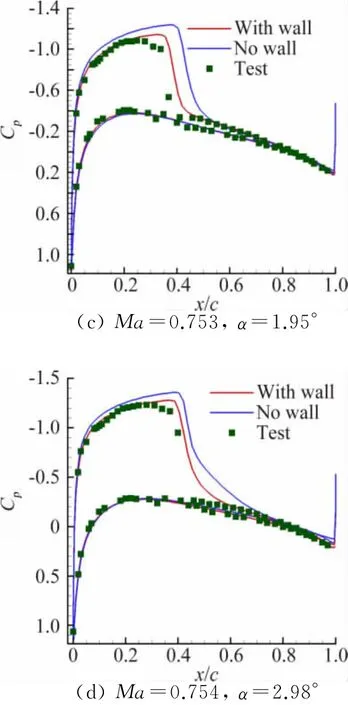
图1 有无洞壁压力分布对比Fig.1 Pressure distribution on NACA0012
4 洞壁干扰修正计算
4.1 网格生成
本文采用点对点对接(1-to-1)的分区多块网格技术生成模型带风洞试验段洞壁网格,不同模型迎角各生成一套网格。为尽量减少计算网格变化对数值求解结果的影响,保证各模型各迎角下带洞壁生成网格拓扑的一致性:模型自由流计算时,将洞壁边界条件延伸至远场,此时洞壁边界条件退化为内部流场;在近物面区域使用“O”型网格,在保证Y+≈1的同时,可以很好地保证近物面网格的正交性,在流场的其他区域使用“H”型网格单元填充。
图2给出小展弦比飞翼标模+洞壁的计算外形和对称面网格,计算子块的个数为39,网格节点达到450万。图3给出小展弦比飞翼标模自由流计算网格,子块个数为49,网格节点达到700万。
4.2 壁压测量及处理
FL-2风洞的试验段尺寸为1.2m×1.2m×3.8m(高×宽×长),开孔壁试验段上下壁为开孔率22.5%的直孔壁,两侧壁为实壁,马赫数范围0.4~1.2。壁压测量试验采用FL-2风洞专用的测壁压装置。为提高壁压插值精度,该装置由8根壁压管组成,分别位于开孔壁试验段上壁板和下壁板,详见图4,八根轴向测压管Φ22mm,每根静压管上开有32个测压孔,对主流场基本无干扰。

图2 小展弦比飞翼标模带洞壁的计算网格示意图Fig.2 The grid with walls
为了消除测压孔壁压数据不规则性、流场的不均匀性和支架的影响,对壁压数据采用了扣初值的处理方法。壁压测量试验除了进行试验段有模型的测力和测压试验外,还要进行空风洞有支架的测壁压试验,用前者的壁压系数减去后者的壁压系数,其差值作为在FL-2风洞模型试验壁压系数的最终输出值。以2#、4#、6#和8#测压管的扣除空风洞后的壁压数据为例,图5是Ma=0.6时α=0°和24°的壁压数据曲线。
图3 小展弦比飞翼标模自由流计算网格示意图Fig.3 The grid without walls
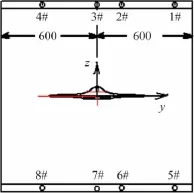
图4 测压管位置示意图(mm)Fig.4 Static pressure tube installation(mm)
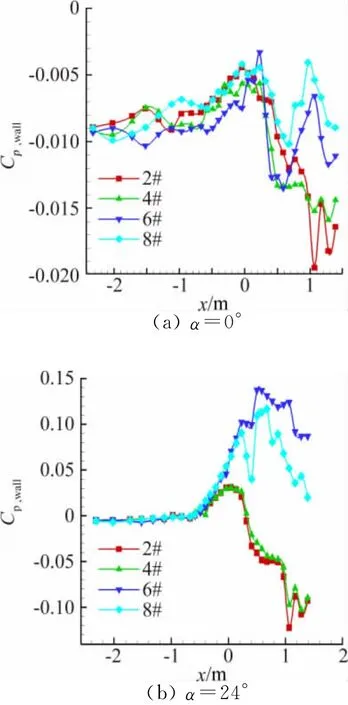
图5 Ma=0.6时FL-2风洞扣除空风洞后的壁压分布曲线Fig.5 Pressure distribution on porous walls at Ma=0.6in FL-2
实际计算过程中,将上述数据沿流向进行三次样条插值,沿展向进行拉格朗日插值至开孔壁边界计算网格单元。不同跨声速风洞的开孔壁参数会有一定差别,开孔率等开孔壁参数对壁压有影响,该影响已反映在所测量的壁压中。在壁压处理过程中,不同开孔壁参数的壁压处理方法是相同的。
5 计算结果及分析
图6和图7分别给出α=4°和α=16°,展向y=0.3处机翼剖面压力分布,由图可见随着马赫数的增加洞壁干扰影响逐渐增大,在Ma=1.05时最大,尤其对背风面的分离流态产生较大影响,风洞壁的存在影响了分离涡的发展,其影响不可忽略。
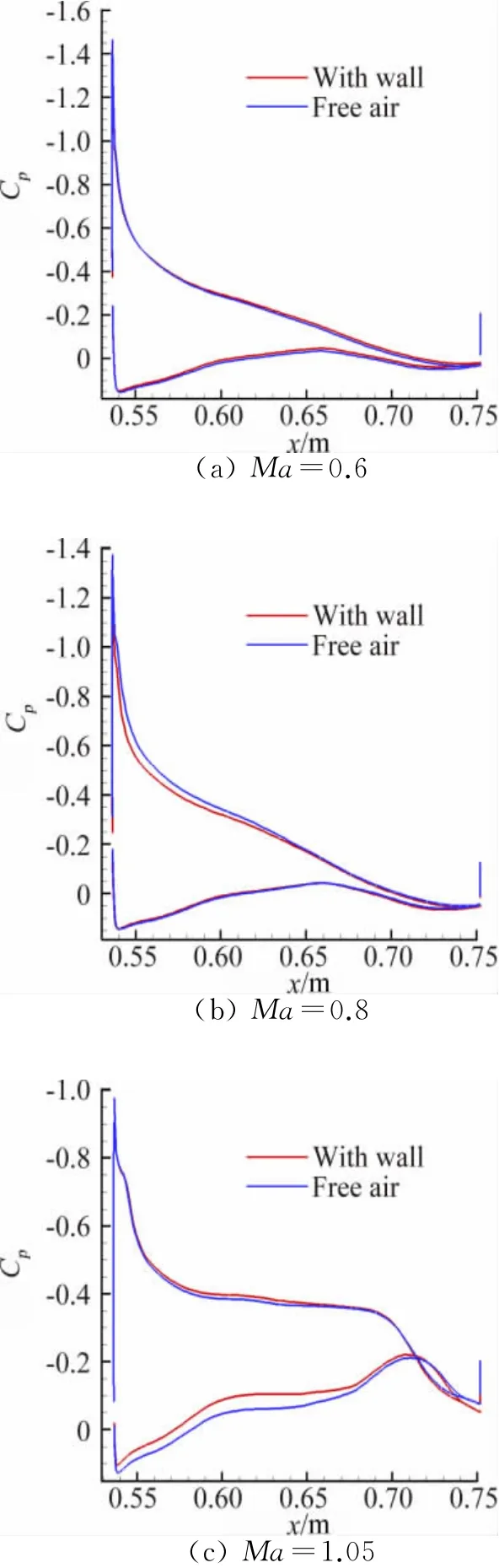
图6 α=4°机翼剖面Cp分布对比Fig.6 Pressure distribution atα=4°
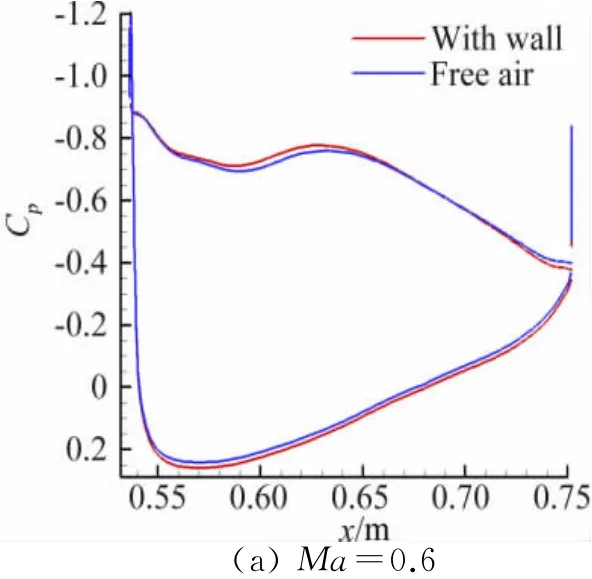

图7 α=16°机翼剖面Cp分布对比Fig.7 Pressure distribution atα=16°
图8 ~图10给出不同马赫数下,α=16°时带与不带洞壁计算的空间马赫数分布云图。由于洞壁的存在,对模型上下表面的马赫数空间分布均有一定影响,随着马赫数的增大,对上翼面背风面的影响更为突出,对模型绕流速度场影响较大。
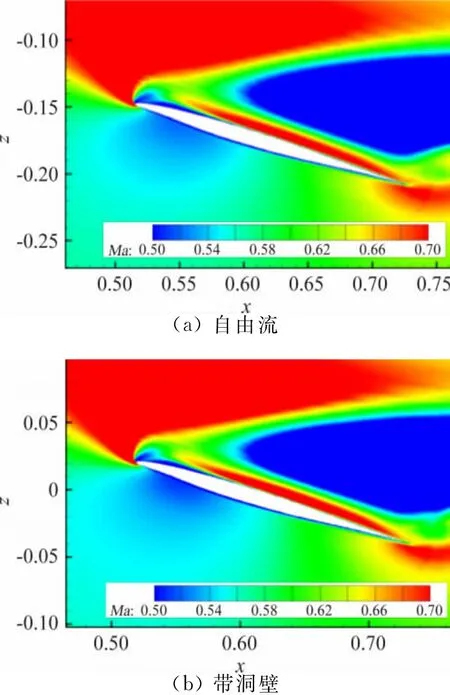
图8 Ma=0.6,α=16°马赫数空间分布云图Fig.8 Mach number distribution at Ma=0.6,α=16°

图9 Ma=0.8,α=16°马赫数空间分布云图Fig.9 Mach number distribution at Ma=0.8,α=16°
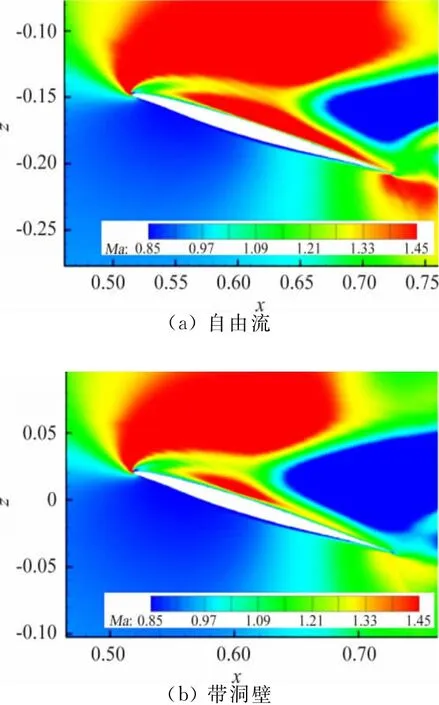
图10 Ma=1.05,α=16°马赫数空间分布云图Fig.10 Mach number distribution at Ma=1.05,α=16°
由图11洞壁干扰量曲线可见,随着马赫数的增加洞壁干扰量逐渐增大。同一马赫数下,洞壁干扰量随着迎角的增加而增大,在Ma=1.05时最大。
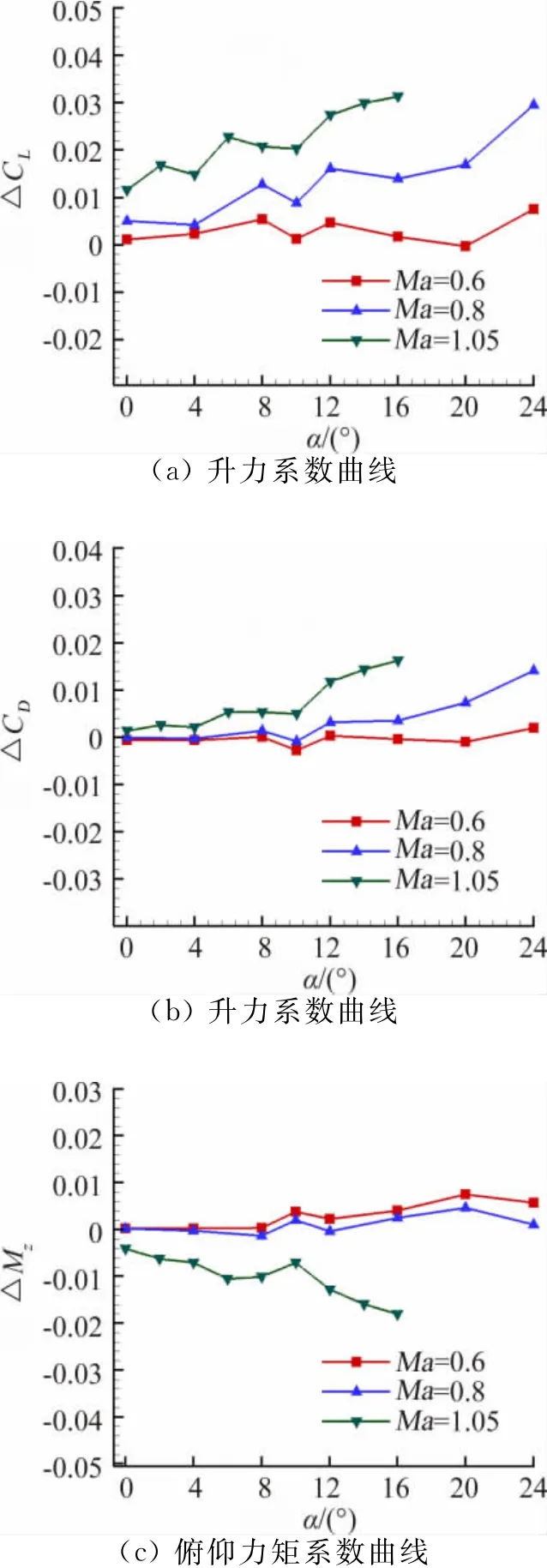
图11 洞壁干扰量曲线Fig.11 Wall interference curve
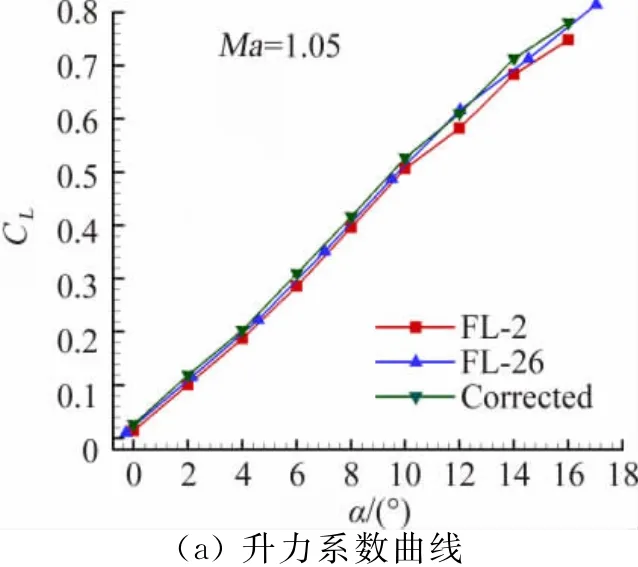
图12给出了Ma=1.05的非线性修正结果与FL-2风洞的试验值及FL-26风洞试验值的比较。总的来说,洞壁干扰修正计算结果与大风洞试验结果的一致性是令人满意的,尤其在中等迎角时经过修正的力矩系数与大风洞试验吻合较好,这就说明本方法有效地对小风洞的试验结果进行了洞壁干扰修正计算,并得到令人满意的计算结果。
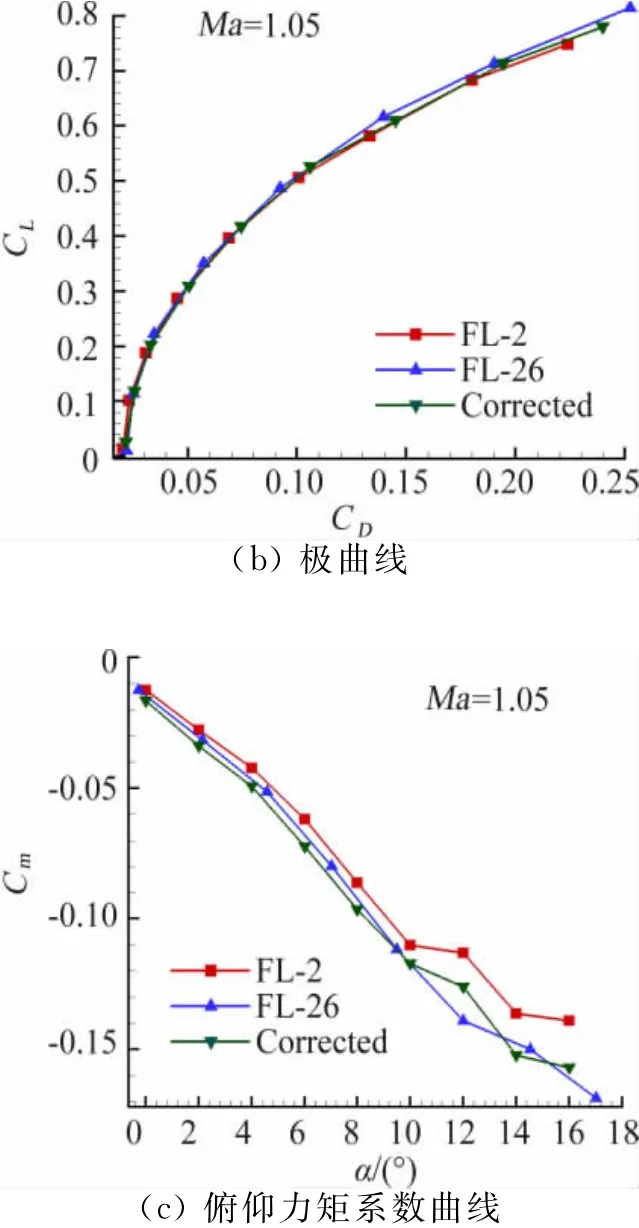
图12 Ma=1.05洞壁干扰修正结果曲线Fig.12 Results comparison
6 结 论
本文根据FL-2风洞的实际情况,结合N-S方程求解开孔壁边界条件来获得跨声速风洞开孔壁洞壁干扰修正量。
(1)通过消除开孔壁测压孔压力数据不规则性、流场的不均匀性和支架的影响等一系列措施,获得了准确的壁压信息。
(2)本文采用的洞壁干扰修正方法,克服线性壁压信息法的局限性。洞壁干扰修正计算结果与大风洞试验结果的一致性是令人满意的,验证了本方法的可靠性和实用性。
(3)本方法可用于试验模型跨声速、分离流态情况的洞壁干扰,修正结果中已经包含了与洞壁干扰不均匀性有关的高阶修正,该方法具有良好的工程实用性,不仅仅局限于飞翼布局飞机,可以适用于各种气动外形,可用于测压试验、测力试验的跨声速洞壁干扰修正。
(4)后继工作将围绕洞壁干扰修正程序的并行化改造开展,以提高计算效率,缩短计算时间,为工程应用奠定基础。
[1] Ewald B F.Wind tunnel wall corrections[R].NASA NO.19980236568,1998.
[2] Yin L P,He Z,Yu Z S,et al.Research on subsonic wall interference correction for model tests at high angle of attack[J].Experiments and Measurements in Fluid Mechanics,2000,14(3):37-41.(in Chinese)尹陆平,贺中,于志松,等.亚声速大迎角模型试验洞壁干扰修正方法研究[J].流体力学实验与测量,2000,14(3):37-41.
[3] Uao Y W,Luo K,Ma Y Q.Research on computational method of wall interference and correction in wind tunnel experiment[J].Science Technology and Engineering,2010,10(8)2031-38.(in Chinese)高永卫,罗凯,马玉清.基于有限元计算的洞壁干扰修正方法研究[J].科学技术与工程,2010,10(8):2031-38.
[4] Chen D H,Zhao R H,Wu K Y,et al.The correlation study of nonlinear aerodynamic characteristics of aircrafts with low aspect ratio[J].Acta Aerodynamica Sinica,2002,20(1):72-77.(in Chinese)陈德华,赵协和,伍开元,等.小展弦比飞机非线性气动特性风洞与飞行相关性研究[J].空气动力学学报,2002,20(1):72-77.
[5] Yun Q L.Error and correction of wind tunnel test data[M].National Defense Industry Press,1996.(in Chiness)恽起麟.风洞实验数据的误差与修正[M].国防工业出版社,1996.
[6] Cheng H M.Interference and correction on wind tunnel testiong[M].National Defense Industry Press,2003.(in Chiness)程厚梅.风洞试验干扰与修正[M].国防工业出版社,2003.
[7] Ni Z S,He D X.Research and application on wall interference correction method of equivalent kinetic pressure[J].Acta Aerodyanmica Sinica,2000,18(1):86-91.(in Chinese)倪章松,贺德馨.等效动压洞壁干扰修正方法的研究与应用[J].空气动力学学报,2000,18(1):86-91.
[8] Ulbrich N and Boone A R.Validation of a wall interference correction system for a transonic wind tunnel[R].AIAA 2004-605.
[9] Allan M R,Badcock K J.A rans investigation of wind tunnel interference efects on delta wing aerodynamics[R].AIAA 2003-4214.
[10]MasatakaKohzai.Wall and support interference corrections of NASA common research model wind tunnel testsin JAXA[R].AIAA 2013-0963.
[11]Maseland J E J,Laban M.Development of CFD-based interference models for DNW-HST transonic wind-tunnel[R].AIAA 2006-3639.2006
[12]Fan Zhaolin,Zhang Yulun,He Zhong.Preliminary research on numerical simulation of transonic wall interference for aircraft model tests[J].Acta Aeronautica et Astronautica Sinica,1997,18(2):210-214.(in Chiness)范召林,张玉伦,贺中.跨音速飞机模型实验洞壁干扰数值模拟的初步研究[J].航空学报,1997,18(2):210-214.
[13]Jiao Yuqin,Qiao Zhide.Navier-stokes calculation of wind tunnel testing of semispan wing with side-wall interference[J].Acta Aeronautica et Astronautica Sinica,2001,22(2):140-143.(in Chiness)焦予秦,乔志德.有侧壁干扰的机翼半模型风洞实验的NS方程数值模拟[J].航空学报,2001,22(2):140-143.
[14]TBIBERT J J,Grandjacques M and Ohman L H.NACA0012 airfoil,in experimental dada base for computer program assessment[R]AGARD AR-138,1979.
[15]Alexander J Krynytzky.Uncertainty evaluation of wall interference in a large transonic wind tunnel[R].AIAA 2010-4341.
Transonic porous wall interference characteristics of the low aspect ratio flying wing model in FL-2wind tunnel
Li Hongyan*,Wang Xiangyun,Yang Ximing,Wang Shihong
(AVIC Aerodynamics Research institute,Shenyang Liaoning 110034,China)
In order to meet the elaborateness requirements of modern wind tunnel testing and improve the accuracy of wind tunnel test data,the nonlinear method of transonic porous wall interference corrections based on wall pressure is developed.The measured wall pressure information is adopted to construct the porous wall boundary conditions,and the flow field around the test model in the wind tunnel is simulated numerically with the N-S equations.Unlike the linear correction methods,this method can be used for a variety of complex shapes of the aircrafts to correct the porous wall interference in the subsonic or transonic wind tunnel.The characteristics of wall interference corrections is studied combining with test data of the low aspect ratio flying wing model conducted in the FL-2wind tunnel.The results indicate that the wall interference has a rising trend with the Mach number increasing,the interference reaches to the maximum at about Ma=1.0,and the corrected results of the FL-2wind tunnel test data are in good agreement with the test results of the FL-26wind tunnel approximately without interference.
wall pressure;wall interference;flying wing;nonlinear method
V211.7
Adoi:10.7638/kqdlxxb-2015.0091
0258-1825(2016)01-0131-07
2015-07-21;
2015-09-15
李鸿岩*(1980-),辽宁丹东人,男,硕士/高级工程师,研究方向:计算流体力学.E-mail:cfd_dawson@163.com
李鸿岩,王祥云,杨希明,等.小展弦比飞翼标模FL-2风洞跨声速开孔壁干扰特性修正研究[J].空气动力学学报,2016,34(1):131-137.
10.7638/kqdlxxb-2015.0091 Li H Y,Wang X Y,Yang X M,et al.Transonic porous wall interference characteristicsof the low aspect ratio flying wing model in FL-2wind tunnel[J].Acta Aerodynamica Sinica,2016,34(1):131-137.
