基于非平行双目结构的三维坐标解算算法
2020-04-14黄振宁马晓锋刘天立魏传虎
刘 俍,黄振宁,马晓锋,刘天立,魏传虎
(国网智能科技股份有限公司,济南250401)
视觉是人类获取外界信息的重要途径,近年来,计算机视觉得到了前所未有的快速发展[1]。基于双目视觉的三维重建技术就是利用双目相机模仿人类的双眼来捕获外界信息,再将捕获的信息输入到计算机中[2]。利用计算机软件实现人类大脑的模拟和仿真,可以使计算机像人类大脑一样对信息进行筛选和处理。再根据三角几何原理得到目标物体的深度信息,从而实现三维重建,实现对目标场景和物体的三维恢复。
基于双目视觉的重建技术已经被广泛应用于医学技术研究、精准零件的制造、虚拟现实技术、目标定位、特征识别及军事研究等方面[3]。目前,基于计算机视觉的三维重建方法大致分为2 类:立体视觉方法和运动恢复结构方法[4-5]。立体视觉方法采用2台或多台相机,通过立体匹配求得视差,根据三角测量原理来恢复空间点的三维信息,其精度较高。
双目立体视觉系统中,非平行双目结构下的三维重建模型如图1 所示。对每台相机来说,如果光心和像点已知,就可确定两者组成的直线上,在针孔成像模型下,物点必然会在此直线上,2 台相机进行交汇,就会产生2条这样的射线,且2条直线都经过像点,两直线相交点就是物点。图1中P 点即空间物点,它的三维位置是唯一确定的。对于这种相机交汇问题的研究,传统的方法是使用最小二乘法来解一个由重投影矩阵所构成的超定方程组,它们都是基于一个前提:4个平面的交点等价于2条直线的交点[6]。而实际情况存在很多噪声,并不能简单地理解为等价[7],本文从几何角度出发,将相机交汇问题转换成求解异面直线公垂线中点问题,并给出理论推导和实验验证。
1 方法
假设已经经过了双目相机的标定,内外参数也已经求得。令ML与MR分别为2台摄像机的投影矩阵,点P 在左右成像平面上的坐标分别为(uL,vL) 和(uR,vR),在内外参数已经求得的情况下,ML与MR为已知的,可得:

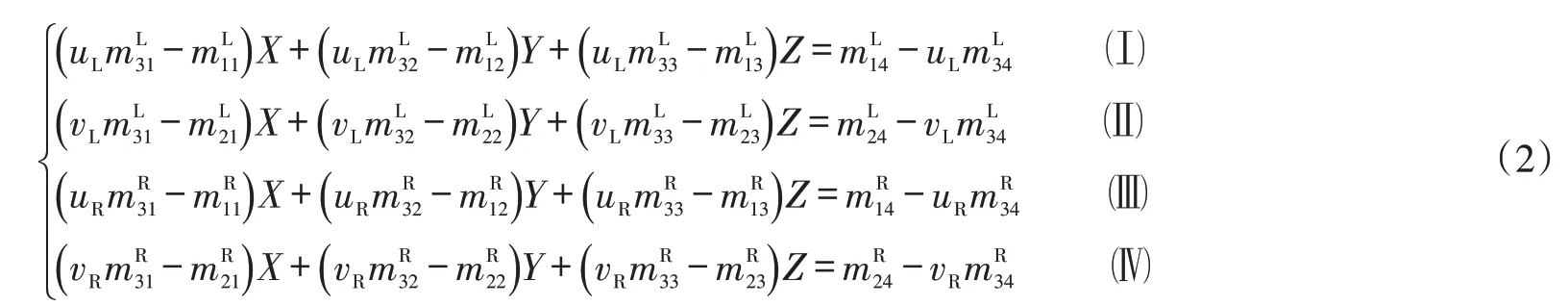

联立式(2)子公式(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ)可以求出点P 在世界坐标系下坐标( X,Y,Z)T。
式(2)为包含X ,Y ,Z 的4 个线性方程,若直线o1p1与直线o2p2一定相交,则这4 个方程必定有唯一解。随意联立3个式子组都能得到唯一解[10-11]。
1.1 最小二乘法
实际应用中,投影矩阵存在一定误差。根据立体匹配算法得到的左右图像的匹配点也存在误差,这些误差就会导致左右相机、左右同名像点在世界坐标系下不能共面。基于这种情况,就不存在三维空间坐标点P 同时满足式(2)中的(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ),它们构成的线性方程组无解。通常情况下,会用最小二乘法求取一个近似解作为物点P 在世界坐标系下的坐标的一个估计( X,Y,Z)T。
最小二乘法是求取线性方程近似解最普遍的方法,用该方法求出来的近似解将会使式(2)的离差平方和最小[12-13]。离差是指将近似解代入方程的左边所得到的值与代入方程右边所得的值的差值,在理想情况下,近似解应该使得式(2)离差为0,离差越小说明精度越高。
将式(2)所构成的方程记为:
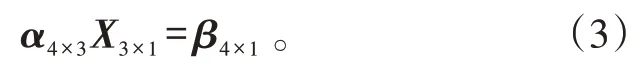
式(3)中:
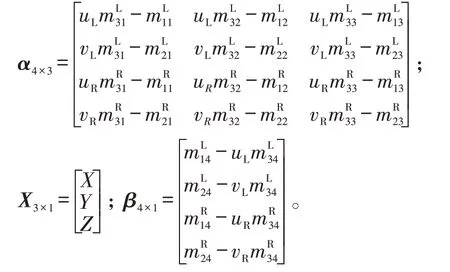
则式(3)的最小二乘法解为:

满足式(4)的X3×1可以使得方程式(2)中4个方程的离差平方和最小[14-15]。
1.2 归一化最小二乘法
将式(2)看成4个平面方程,通过寻找一个三维空间点,这个三维空间点到4 个平面的距离的平方和达到最小作为方程组的近似解。基于这种原理,引出了下面的归一化最小二乘法[16]。将α4×3的所有行向量进行归一化处理,在式(3)的两边同时左乘一个矩阵
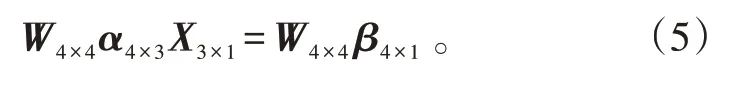
式(5)中:
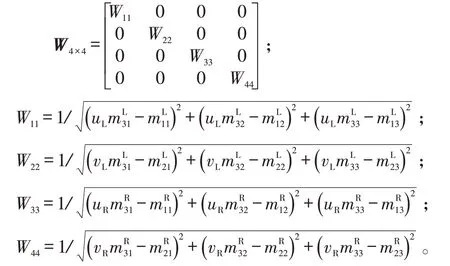
由式(5)可得归一化最小二乘法解:
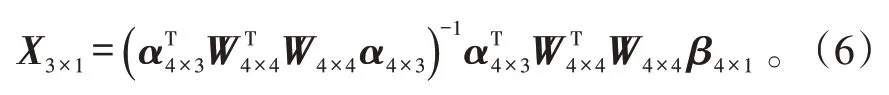
1.3 基于异面直线公垂线重点的三维坐标解算算法
1.3.1 算法几何背景分析
对于每台相机而言,如果光心和像点是已知的,就可以确定光心和像点组成的直线。针孔模型下,三维空间点必然会在直线上,2台相机就产生2条这样的直线,2直线都经过三维空间点,所以,利用2直线在三维空间点相交的原理,就可以对其进行交汇定位。但是,由于相机畸变,受图像噪声等各种原因影响,2 条直线不一定会相交。从几何角度分析,可以将到2 条异面直线距离平方之和最小的点作为2条异面直线的交点,再证明此交点为异面直线公垂线的中点。这时,交汇定位问题就可以转化成求异面直线公垂线中点坐标的问题[17-18]。
1.3.2 算法推导


图2 坐标解算图Fig.2 Coordinate solution diagram
G1、G2、G3、G4分别对应式(2)中(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ)4个平面方程的法向量。即:

由2个平面的交线的求解公式可知,2个平面法向量的叉乘即为交线方向向量。G1×G2是式(2)中(Ⅰ)(Ⅱ)2 个平面交线的方向向量,由单位向量求解定理可知,L1求解公式如式(11)所示。同理,G3×G4是式(2)中(Ⅲ)(Ⅳ)2 个平面交线的方向向量,L2求解公式如式(11)所示。

根据点到直线的距离可知:
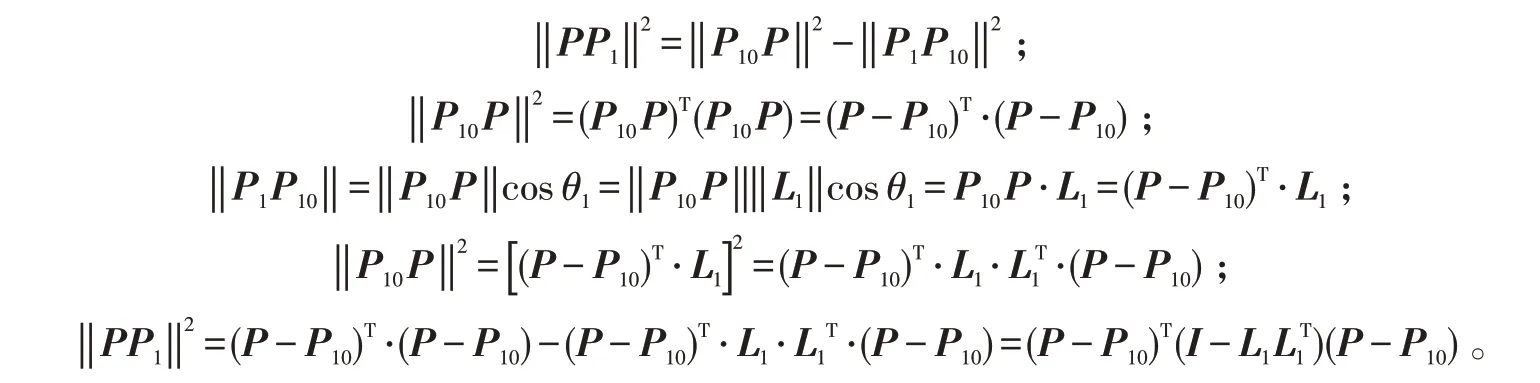
式中,I 为三阶矩阵。
同理:
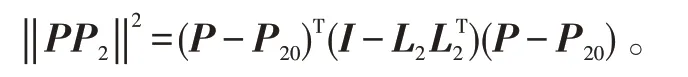
故,点P 到直线L1和L2的距离和为:
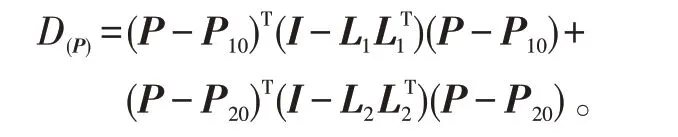
令对P 的偏导为0可得:
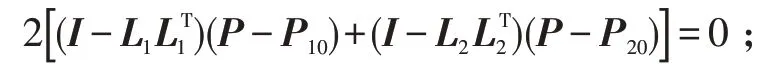

此时,点P 到两直线距离平方和达到最小。其次证明这个点就是2条异面直线公垂线的中点。根据向量的减法法则可得:
PP1=PP10-P1P10;
P-P1=(P-P10)-(P1-P10);
P1-P10=P10P1=‖ ‖P1P10L1;

将点P 代入上述公式:
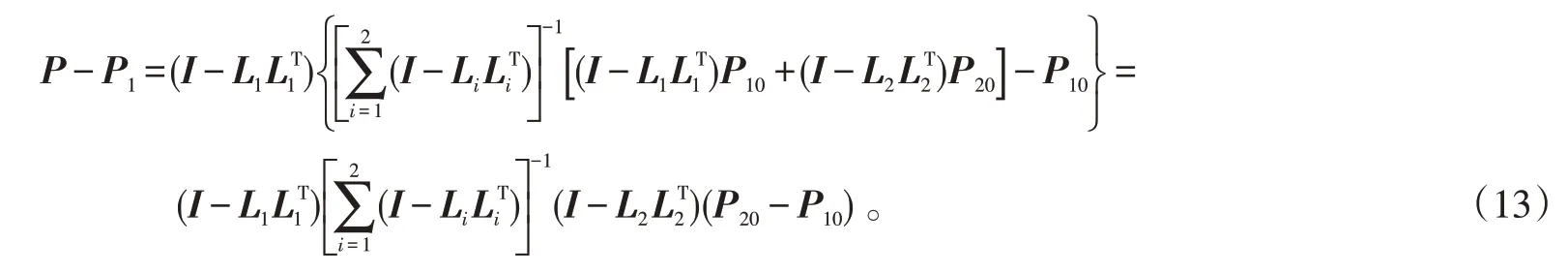
同理可得:
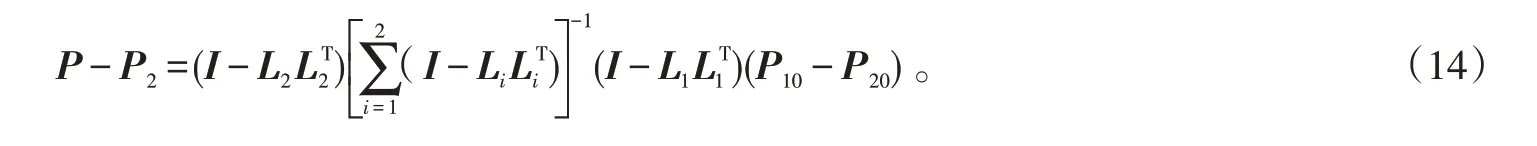
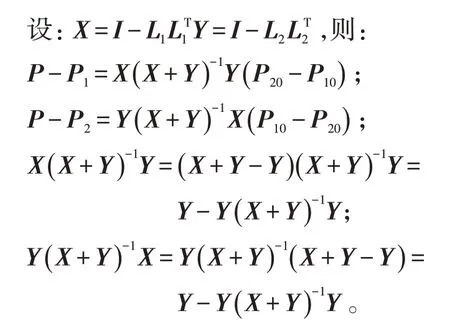
则:

此时说明,点P 就是2条直线的公垂线的中点。
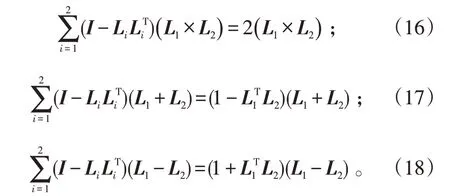
2)当 |L1TL2|=1 时,L1L2互相平行,L1-L2必为零向量,则L1+L2必不为零向量
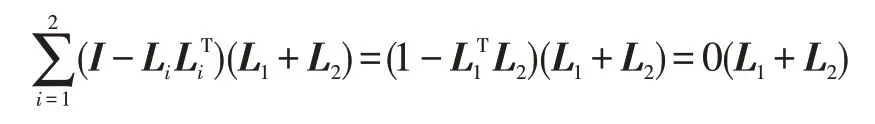
出现了为0 的特征值,所以矩阵必不可逆。此种情况因为2条直线平行,将无穷远点视为物点P 在世界坐标系下的估计。
2 实验
2.1 实验平台
四旋翼飞行器具备结构简单、机动性强、可垂直起降、定点悬停、容易操作等特点,故本文采用四旋翼无人机作为实验平台,对目标物体进行深度信息恢复,实验采用四旋翼无人机平台如图3 所示。四旋翼无人机机身是由对称的十字形钢体结构构成;在十字形结构的4 个端点分别安装1 个由2 片桨叶组成的旋翼为飞行器提供飞行动力,每个旋翼均安装在1 个电机转子上,通过控制电机的转动状态控制每个旋翼的转速,来提供不同的升力以实现各种姿态;每个电机均又与电机驱动部件、飞行控制单元相连接,通过飞行控制单元提供的控制信号来调节转速大小。

图3 四旋翼无人机平台Fig.3 Quadrotor UAV platform
图像采集系统使用的相机是小觅双目摄像头,如图4所示。

图4 小觅摄像头Fig.4 Xiaomi camera
使用图3中的四旋翼无人机搭载图4中的小觅摄像头,分别在室内和室外放置不同距离的目标物体,对其进行深度信息恢复。通过对使用算法所得到的距离与真实距离的对比,来验证算法的可行性。
2.2 相机标定
本文采用张正友标定法对相机进行标定,标定结果如表1所示。
2.3 三维坐标解算
分别用本文设计的算法、最小二乘法和归一化最小二乘法求解图5中的水杯三维点坐标。在获得三维点坐标以后,通过求出坐标中X 坐标的最大值Xmax与X 坐标的最小值Xmin的差值和Y 坐标的最大值Ymax与Y 坐标的最小值Ymin的差值,实现对杯子直径的测量,将距离的最大值视为杯子的直径。

表1 相机内外参数Tab.1 Internal and external parameters of the camera

图5 双目原图Fig.5 Original binocular image
使用最小二乘法求解的部分三维坐标点数据如表2所示。

表2 最小二乘法求解的部分三维坐标点数据Tab.2 Partial three-dimensional coordinate points solved by least square method mm
由表2,Xmax=37.85,Xmin=-35.88,杯子直径计算可得:
Xmax-Xmin=73.73。
由表2,Ymax=38.95,Ymin=-34.16,杯子直径计算可得:
Ymax-Ymin=73.11。
测量值与真实值对比如表3所示。

表3 计算值与测量值Tab.3 Calculated and measured values mm
使用归一化最小二乘法求解的部分三维坐标点数据如表4所示。
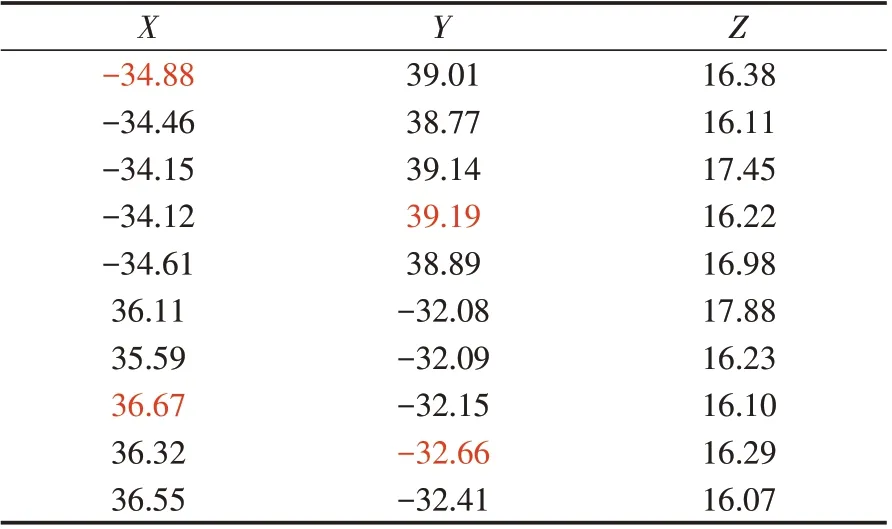
表4 归一化最小二乘法求解的部分三维坐标点数据Tab.4 Partial three-dimensional coordinate points solved by normalized least square method mm
由表4,Xmax=36.67,Xmin=-34.88,杯子直径计算可得:
Xmax-Xmin=71.55。
由表4,Ymax=39.19,Ymin=-32.66,杯子直径计算可得:
Ymax-Ymin=71.85。
测量值与真实值对比如表5所示。

表5 计算值与测量值Tab.5 Calculated and measured values mm
使用本文设计的算法求解的部分三维坐标点数据如表6所示。
由表6,Xmax=35.43,Xmin=-33.01,杯子直径计算可得:
Xmax-Xmin=68.44。
由表6,Ymax=40.29,Ymin=-28.52,杯子直径计算可得:
Ymax-Ymin=68.81。
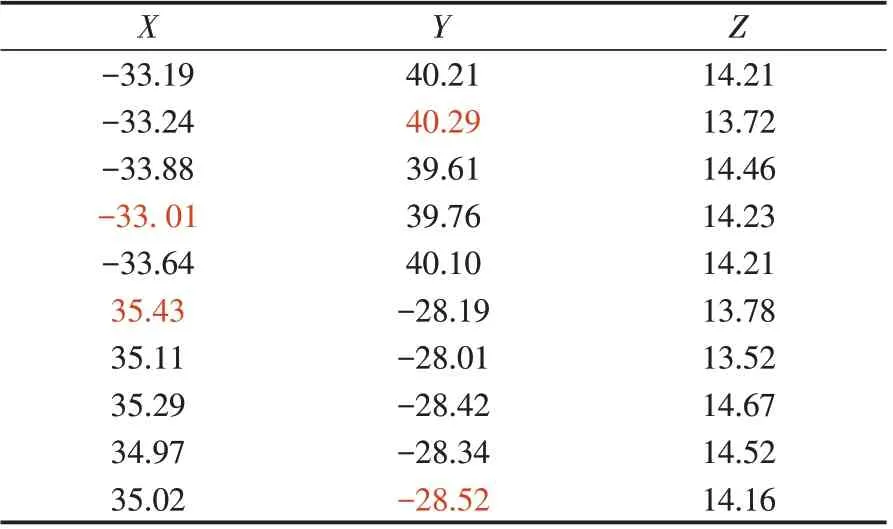
表6 异面直线公垂线中点法求解部分三维坐标点数据Tab.6 Partial three-dimensional coordinate points solved by midpoint method of common perpendicular line of different planes mm
测量值与真实值对比如表7所示。
由表3 可知,使用最小二乘法进行三维坐标点的解算,然后求取杯子的直径,与真实值进行对比,误差为12.4%。由表5 可知,使用归一化最小二乘法的误差为9%。由表7 可知,使用本文提出的基于异面直线公垂线中点的三维坐标点解算算法的误差为4.3%。由此得出,在非平行结构双目结构下,本文提出的算法在解算三维坐标点时精度最高。
2.4 深度信息恢复
采用的小觅相机标准版的基线为70 mm,其测量范围为0.26~3 m,所以不适合大范围测距。本文实验的深度恢复对象分别为50 mm 、70 mm 、1 500 mm 、2 000 mm。需说明的是,实际距离值来自于高精度的激光雷达所测量的数据。
实验1:采用张正友标定算法得到的相机内外参数,然后用最小二乘法、归一化最小二乘法、基于异面直线公垂线中点法来进行深度信息恢复。目标物体实际距离为500 mm。实验结果如表8所示。
实验2:采用张正友标定算法得到的相机的内外参数,然后用最小二乘法、归一化最小二乘法、基于异面直线公垂线中点法来进行深度信息恢复。目标物体实际距离为700 mm。实验结果如表9所示。

表8 3种解算算法对实际距离为500 mm 的目标深度信息恢复精度比较Tab.8 Comparison of the accuracy of depth information restoration of target with an actual distance of 500 mm by three algorithms

表9 3种解算算法对实际距离为700 mm 的目标深度信息恢复精度比较Tab.9 Comparison of the accuracy of depth information restoration of target with an actual distance of 700 mm by three algorithms
实验3:采用张正友标定算法得到的相机内外参数,然后用最小二乘法、归一化最小二乘法、基于异面直线公垂线中点法来进行深度信息恢复。目标物体实际距离为1 500 mm。实验结果如表10所示。
实验4:采用张正友标定算法得到的相机内外参数,然后用最小二乘法、归一化最小二乘法、基于异面直线公垂线中点法来进行深度信息恢复。目标物体实际距离为2 000 mm。实验结果如表11所示。
综合表8~11 可以看出,在光照充足的室内环境下,环境干扰因素小,且飞机处于静止状态。所以,3种算法的精度都较高,误差值在5%以内。本文提出的方法精度最高,精度在2%以内,能够满足精度需求较高的场合。由于室外环境光照不均匀,容易造成低纹理和重复纹理、深度不连续、平滑镜面反射等问题,且无人机处于飞行状态,自身的抖动对立体匹配影响很大,这使得测距的精度受到严重的影响,尤其是最小二乘法和归一化最小二乘法解算,误差达到20%左右,本文提出的方法精度虽然有所下降,但仍然保持在8%以内,说明其鲁棒性更好。

表11 3种解算算法对实际距离为2 000 mm 的目标深度信息恢复精度比较Tab.11 Comparison of the accuracy of depth information restoration of target with an actual distance of 2 000 mm by three algorithms
3 结论
实验结果表明,相较于常用的最小二乘法解算和归一化最小二乘法解算方法,基于非平行双目结构的三维坐标解算算法在采用张正友标定算法得到内外参数、SGBM 立体匹配算法得到视差信息的基础上,无论在室内环境还是室外环境,解算得到的深度信息精度均为最高,具有良好的应用前景。
