净升力对临近空间浮空器上升航迹的影响分析

陈 雪，赵新路，杨 涵

（1.成都航空职业技术学院，成都610100；2.四川航天系统工程研究所，成都610100）

临近空间浮空器是指工作在高度为20～100 km 区域的浮空飞行器，主要包括平流程飞艇、充气式太阳能无人机、高空科学气球等。近年来，在科学探测、互联网通信等应用需求牵引下，临近空间浮空器受到高度关注[1-4]，高空科学气球因其在气象探测、对地观测方面作用突出且成本低廉应用逐渐广泛[5-6]。准确预测高空科学气球上升过程飞行航迹，通过仿真精确获取其飞行参数，掌握环境参数对试验平台飞行的影响规律，对于试验平台总体设计、飞行试验方案设计、试验平台运行管理等都具有极其重要的意义。

高空科学气球的净升力是指高空气球浮力与自身重力的合力，一般用来表示充灌气体的质量。在实际工作中，除了高空气球本身的质量因素，净升力是影响高空气球的自然爆破高度和上升速度的主要因素，所以，研究净升力对高空气球上升过程航迹的影响是很有必要的。

国内外学者对高空科学气球的航迹/热性能耦合分析问题的研究最早可追溯至20世纪70年代的Kreith 和Kreider 关于零压气球性能预测的研究，属于里程碑式的经典奠基之作[7]，文献[8-9]研究了适用于高空气球上升和驻空阶段的热模型和动力学模型，并编制了软件；杨希祥等研究了高空科学气球下降过程航迹与热性能耦合问题，得出了高空气球下降过程存在严重超热现象，分析了超热状态变化和下降速度变化之间的影响关系[10]；邓小龙等针对平流层底部准零风层特点，提出一种基于风场综合利用进行长时区域驻空的新型平流层浮空器，系统采用南瓜形超压气球体制，建立系统的浮重模型、推阻模型和能源模型，利用迭代算法完成了总体方案设计[11-13]；戴秋敏等对高空气球放飞后和驻空阶段热行为与航迹仿真问题进行了系统研究[14-15]；吕明云等综合热力学模型与动力学模型，研究了高空气球上升阶段性能预测问题[16]。在热模型方面，平流层飞艇与高空气球类似，姚伟、赵攀峰等建立了平流层飞艇热模型，研究了飞艇驻空阶段的热特性[17-18]。

本文通过建立高空科学气球初始充气量计算模型、上升过程热模型和动力学模型，对上升航迹与内部气体热性能耦合问题进行仿真分析，得到净升力对气球爆破高度与上升速度的影响，并总结得出在实际工作中提高爆破高度及获得理想升速应采取的措施。

1 临近空间科学试验平台方案

研究的高空科学试验平台由高空气球、降落伞、万向节、解锁装置、球载天线、吊舱等组成，如图1 所示。高空气球采用南瓜形超压气球[19]，用于提供系统升空和在高空驻留的浮力；气球装有万向节，用于实时调整风向变化对吊舱产生的影响，避免柔性连接装置的缠绕；解锁装置用于气球到达预定高度时对吊舱进行解锁，使吊舱开始下落，实现回收；降落伞用于下降阶段减速，保证设备安全着陆和回收；吊舱是设备集中安装装置，装有有效载荷、锂电池、导航板、数传电台、图传电台等。

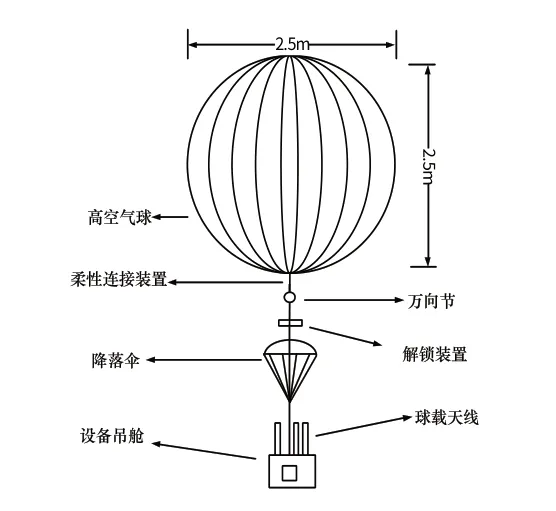
图1 高空科学试验平台Fig.1 Platform of high altitude scientific test

2 初始充气量计算模型

受条件限制，高空科学气球充灌气体的量难以直接测量，但可以根据浮力反算出所充气体的量。高空科学气球充气完成后，可以测量得到净升力（气球本身净浮力），根据理想气体状态方程PV=mRT 可得：

式（1）中：Vball为气球的体积；mH为气球所充气体的质量；RH为比例常数，此时RH=4.157 21；TH为气球内气体温度，气球在地面时与大气温度Tair相等；PH为气球内气体压力。

高空科学气球的总浮力可表示为：

式（2）中：ρair为大气的密度；Fv为气球的净升力；mball为气球的质量。

由式（1）（2），可以得到初始充灌气体的质量为：

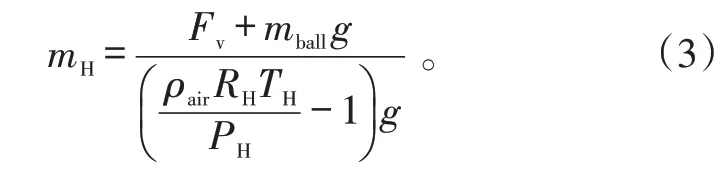
3 对流换热

高空科学气球对流换热主要指蒙皮与外部大气的对流换热[10]，表示如下：

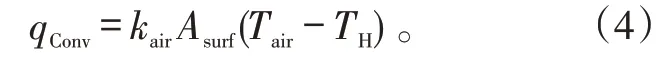
式（4）中：kair为热交换系数；Asurf为气球表面积；Tair为大气温度。

假定气球内部气体温度和压力均匀，根据热力学第一定律[3]：

式（5）中：cvH为气体定容比热；MH为气体的摩尔质量；VH为气体的体积。

等号右端各项分别表示气体与大气之间的自然对流换热、由于气体排放产生的流动功、气球收缩时外界对气球所做的功、由于气体排放损失的内能。

4 上升过程动力学模型

高空科学气球上升过程航迹与热性能的耦合反映在纵向运动和水平运动上。

纵向动力学方程可表示为：

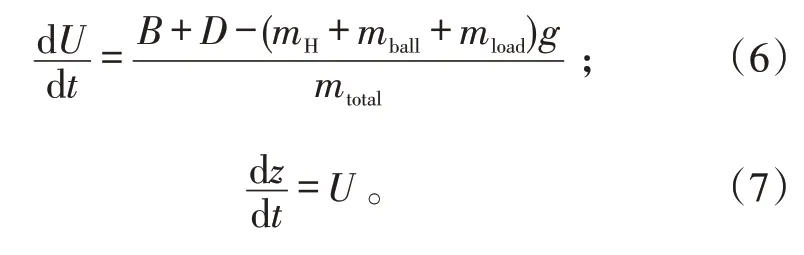
式（6）（7）中：U 为纵向速度；z 为上升高度；D 为气动阻力；mload为任务载荷质量；mtotal为气球总质量。

式（9）中：CD为阻力系数；S 为气球参考面积。

CD可用下式求解：

式中，Re 为雷诺数。

若高空科学气球水平方向视为随风飘动，即假设水平速度等于风速，则水平方向动力学方程可表示为：

式（11）（12）中：x 为经向位移，向南为正；y 为纬向位移，向东为正；vwind为水平风速，θ 为风向。

5 仿真结果与分析

为验证建立的数学模型准确性，开展了2 次小载荷高空科学试验平台飞行试验，自编计算机程序，对高空科学气球的上升飞行过程进行仿真，并与实际试验数据对比，验证仿真模型的可靠性。

5.1 仿真模型准确性验证

第1次飞行试验气球规格选为0.75 kg，载荷量为1.15 kg，飞行试验采用的试验平台主要参数如表1 所示，放飞地点为28.2°N，113.1°E。

表1 试验平台主要参数Tab.1 Main parameters of test platform

高空科学试验平台上升过程中，随时间变化的上升高度和上升速度的实际数据和仿真结果的比较如图2、3所示，三维航迹如图4所示。

图2 上升高度-时间曲线Fig.2 Curve of ascent altitude versus time

图3 上升速度-时间曲线Fig.3 Curve of ascent velocity versus time

图4 三维航迹图Fig.4 Three-dimensional trajectory

由图2 可以看出，试验平台上升高度的实际数据和仿真结果基本吻合，最大偏差3.2%；由图3 可以看出，上升速度的仿真结果大致与上升速度的实际数据平均值相等，最大偏差2.3%；由图4可以看出，仿真航迹和实际航迹吻合较好，最大偏差2.7%。以上数据表明本文建立的仿真模型具有较高精度。

第2 次飞行试验气球规格选为1.6 kg，载荷量为3 kg，飞行试验采用的试验平台主要参数如表2所示，放飞地点为28.2°N，113.1°E。

表2 试验平台主要参数Tab.2 Main parameters of test platform

高空气球试验平台上升过程中，随时间变化的上升高度和上升速度的实际数据和仿真结果的比较如图5、6所示，三维航迹如图7所示。

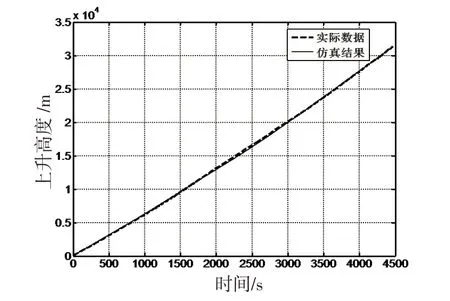
图5 上升高度-时间曲线Fig.5 Curve of ascent altitude versus time

图6 上升速度-时间曲线Fig.6 Curve of ascent velocity versus time

由图5 可以看出，对1.6 kg 高空科学试验平台携带3 kg 载荷，在7 kg 净升力的情况下，上升高度的实际数据和仿真结果基本吻合，最大偏差2.5%；由图6可以看出，上升速度的仿真结果大致与上升速度的实际数据平均值相等，最大偏差1.8%；由图7可以看出，仿真航迹和实际航迹吻合较好，最大偏差4.1%，验证了本文建立的仿真模型在不同净升力情况下的准确性。

通过高空科学试验平台2 次飞行试验的对比，可以看出仿真结果与实际数据较为接近。因为上升下降气流的存在，所以急流区内的实际上升速度与仿真结果略有差别，其他时间段上升速度的平均值与仿真结果非常接近。从航迹图可以看出，仿真结果的航迹与实际航迹的偏差在5%以内，仿真模型的准确性较高，结果具有较高的可信度。

5.2 上升过程航迹性能分析

选用0.75 kg 规格的气球，在净升力分别为6 kg、8 kg 和10 kg 的情况下对高空气球上升高度和体积进行仿真，结果如图8、9所示。

图8 上升高度-时间曲线Fig.8 Curve of ascent altitude versus time

由图8 可以看出，高空气球的上升高度相对于时间基本是线性变化的，净升力为6 kg、8 kg 和10 kg 的气球平均上升速度分别为9.8 m/s、9.2 m/s 和8.3 m/s，净升力越大，气球达到同一高度时所用的时间越长，即上升速度越慢。净升力为6 kg、8 kg 和10 kg 的气球达到爆破高度分别用时约为2 185 s 、2 685 s 和2 775 s。另外，净升力越大，气球的爆破高度越低，净升力为6 kg 、8 kg 和10 kg 的气球爆破高度分别为23 013 m、21 621 m 和20 524 m。所以可以通过控制净升力来实现控制气球上升高度和上升速度。

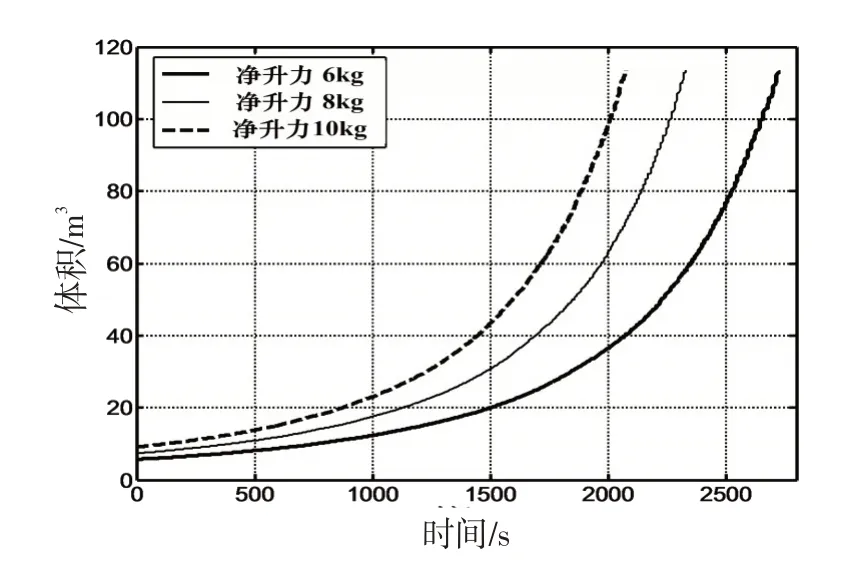
图9 体积-时间曲线Fig.9 Curve of volume versus time

由图9可以看出，高空气球在上升过程中，气球的体积逐渐增大，且变化率越来越大，气球在达到爆破高度时，体积达到了113 m3。同时，净升力越大，气球体积增大越迅速，这是因为在气球上升过程中，大气压力逐渐减小，气球要保持自身内外压差恒定（零压气球），就必须通过气球自身体积膨胀来减小气球内部的压力，而净升力越大，气球上升速度越快，见图8，直接导致了气球随着高度的增加迅速膨胀。

综合分析图8、9 可知，净升力对高空气球上升过程中上升的高度和体积影响是很大的，不同的净升力得到不同的上升航迹，所以合理的选择初始充气量来控制气球的净升力是很有必要的。

5.3 初始充气量对上升过程的影响

采用上述仿真模型，自编计算机程序，对0.75 kg和1.6 kg 规格的高空科学试验平台分别携带1.15 kg和3 kg 载荷在不同充气量下的上升情况进行仿真，得到气球自然爆破高度和上升速度随净升力变化的情况如图10、11所示。

由图10 可以看出，随着净升力的不断增加，即气球的充气量增加，气球的爆破高度不断降低，且变化率逐渐减小。 0.75 kg 规格的气球，当净升力低于1.7 kg 时，气球上升到一定高度后会在此高度驻留，无法达到爆破高度。净升力从1.7 kg 上升到11 kg 的过程中，净升力每增加0.5 kg ，爆破高度最大降低1 195 m，最小降低229 m。1.6 kg 规格的气球当净升力低于4.28 kg 时，气球上升到一定高度后会在此高度驻留，无法达到爆破高度。净升力从4.28 kg 上升到14 kg 的过程中，净升力每增加0.5 kg，爆破高度最大降低470 m，最小降低164 m。比较2 种规格的高空气球爆破高度可得，气球规格越大，爆破高度越高。

图10 爆破高度-净升力曲线Fig.10 Curve of blasting altitude versus net lift

图11 上升速度-净升力曲线Fig.11 Curve of ascent velocity versus net lift

由图11 可以看出，随着净升力的不断增加，气球的平均升速不断增大，且变化率逐渐减小。0.75 kg 规格的气球净升力从1.7 kg 增大至11 kg 的过程中，净升力每增加0.5 kg，平均升速最大增加1.45 m/s，最小增加0.12 m/s；1.6 kg 规格的气球从4.28 kg 增大至14 kg的过程中，净升力每增加0.5 kg，平均升速最大增加1.58 m/s，最小增加0.11 m/s。比较2 种规格的高空气球平均升速可得，气球规格越大，气球的平均升速越小，这是因为规格越大的气球起始重量较大，获得的初始升速随之减小。

综合比较图10、11得到，随着净升力的不断增加，上升速度的增大比爆破高度的减小相对于净升力的变化更加敏感。上述分析表明，在高空科学气球上升过程中，应合理控制充气量从而控制净升力，达到预期爆破高度和预期上升速度，来满足任务需求。

6 结论

本文综合考虑临近空间浮空器的动力学性能与热性能，以某高空科学气球为例，研究分析了其上升过程中净升力对航迹性能参数的影响。主要研究工作和结论如下：

1）建立了高空科学气球初始充气量计算模型、热模型和上升过程动力学模型；

2）通过仿真计算和飞行试验对比，验证了高空科学气球上升过程中所建立的热模型和动力学模型的准确性和可靠性；

3）通过仿真，得到了动力学与热耦合条件下，高空科学气球上升过程中，净升力对航迹性能参数的影响变化规律，分析了参数变化规律原因，研究了上升过程航迹性能，分析了净升力对爆破高度和上升速度的影响。结果表明，随着净升力的增加，爆破高度迅速降低，而气球上升速度逐渐增大，且上升速度的增大比爆破高度的减小相对于净升力的变化更加敏感，表明气球的净升力对航迹性能参数存在重要影响。