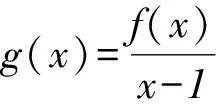构造函数巧解一类与导数有关的不等式问题
2020-04-13广东陈增海
◇ 广东 陈增海
与导数有关的不等式问题一直是高考中的热点和难点,尤其是抽象函数的导数具有高度的抽象性,将其与不等式结合会使问题变得更加复杂.这类问题对学生的综合能力要求较高,能较好地考查学生的数学抽象、逻辑推理等核心素养. 本文将常见的抽象函数导数与不等式结合的问题归类,并构造相应的函数模型进行求解,以期给同学们启示.
1 形如f′(x)+kxα
常见模型:1)若f′(x)+k>0(或<0),其中k为非零常数,可构造函数g(x)=f(x)+kx;





A. (-∞,-1)
D. (-∞,-1)∪(1,+∞)


2 形如xf′(x)±nf(x)
常见模型:1)若xf′(x)+nf(x)>0(或<0),可构造函数g(x)=xnf(x);


A.a C.a 等价于(x+2 019)2f(x+2 019)<52f(5),即g(x+2 019) A. 8f(22 018) B. 8f(22 018)>f(22 019) C. 8f(22 018)=f(22 019) D. 无法确定8f(22 018)与f(22 019)的大小 常见模型:1)若f′(x)+f(x)>t(或 A. (2 014,+∞) B. (-∞,0)∪(2 014,+∞) C. (-∞,0)∪(0,+∞) D. (0,+∞) A. (-∞,1) B. (-∞,0) C. (0,+∞) D. (1,+∞) 常见模型:1)若f′(x)sinx+f(x)cosx>0(或<0),可构造函数g(x)=f(x)sinx; 3)若f′(x)cosx-f(x)sinx>0(或<0),可构造函数g(x)=f(x)cosx; A.a C.c 常见模型:1)若f′(x)·xlnx+f(x)>0(或<0),可构造函数g(x)=lnx·f(x); A. (-∞,-1)∪(1,+∞) B. (-∞,-1)∪(0,1) C. (-1,0)∪(0,1) D. (-1,0)∪(1,+∞) 1)若f′(x)·xlnx+(1+lnx)f(x)>0(或<0),可构造g(x)=xlnx·f(x); 常见模型:1)若f′(x)(x+t)+f(x)>0(或<0),可构造函数g(x)=(x+t)f(x); A.c C.a 解决抽象函数的导数与不等式问题的关键是构造满足条件的辅助函数,然后利用辅助函数的单调性脱去“f”,将与导数有关的不等式转化为一般的不等式求解,所以构造辅助函数以及把握好函数的单调性是解题的关键,只有利用好函数单调性,才能顺利解决问题.







3 形如f′(x)±f(x)
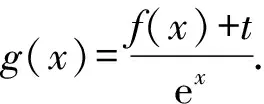





4 形如f′(x)sin x±f(x)cos x或者f′(x)·cos x±f(x)sin x

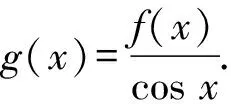





5 形如f′(x)·xln x±f(x)
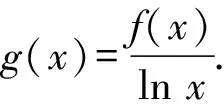


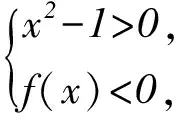


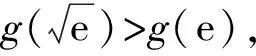




6 形如f′(x)(x+t)±f(x)