柯西不等式的应用透视

◇ 山东 王 敏 刘美亭

1 求值

2 求最值

3 证明不等式

利用柯西不等式证明某些不等式特别方便,利用柯西不等式的技巧也有很多,如添项、配凑常数式、改变结构等.

3.1 添项

3.2 “1”的代换

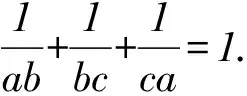
由柯西不等式,得

所以ab+4bc+9ac≥36,当且仅当a=2,b=3,c=1时,等号成立.

3.3 凑配常数式

(1)解不等式f(x)≥4;

(2)记函数f(x)的最小值为m,若a,b,c均为正实数,且a+2b+3c=2m,证明:

(a2+b2+c2)(12+22+32)≥(a+2b+3c)2,

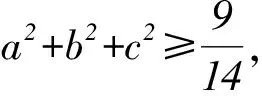
3.4 改变结构

证明由柯西不等式,得

当且仅当a=b=1时，等号成立.

综上，(a+b)(a5+b5)≥4.

4 求取值范围

A.[-5,5] B.(-5,5)

所以由柯西不等式

(32+22)[x2+(-x+y)2]≥
[3x+2(-x+y)]2=(3x-2x+2y)2=(x+2y)2,

又由例8中的变式,得