坐标系与参数方程考点探秘

◇ 河北 曹国庆(特级教师)

从近几年的高考试题来看,极坐标与参数方程始终以选考题的形式出现,主要考查极坐标方程和直角坐标方程的互化，直线、圆及椭圆的参数方程与普通方程的互化等内容.

1 参数方程、极坐标方程与普通方程的互化

极坐标与直角坐标的相互转化中,将直角坐标方程转化为极坐标方程比较容易,只需将公式x=ρcosθ,y=ρsinθ直接代入并化简即可.将极坐标方程化为直角坐标方程则相对困难一些,求解此类问题,常用方法有代入法、平方法等,还经常会用到同乘(或除以)ρ等技巧.

2 参数方程的应用

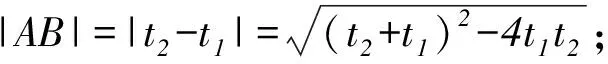
④ |PA|·|PB|=|t1t2|.

(1)写出C1的普通方程和C2的直角坐标方程;

(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.

3 极坐标方程及其应用

求曲线的极坐标方程可分为三步：

1)建立适当的极坐标系,设P(ρ,θ)是曲线上任意一点;

2)由曲线上的点所适合的条件,列出曲线上任意一点的极径ρ和极角θ之间的关系式;

3)将列出的关系式进行整理、化简,得出曲线的极坐标方程.

(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;

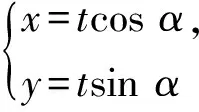
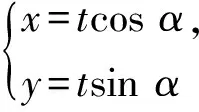
设直线l的斜率为k,则直线l的方程为kx-y=0.由圆C的方程(x+6)2+y2=25，可知圆心坐标为(-6,0),半径为5.

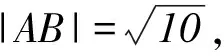
4 极坐标与参数方程的综合应用

对于涉及参数方程和极坐标方程的综合问题,求解的一般方法是将方程化为普通方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.

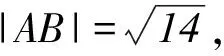
(2)设M(x,y)为曲线C上任意一点,求x+y的取值范围.

圆心(2,0)到直线y=x-m的距离为

所以|m-2|=1,解得m=1或3.