桥梁转体不平衡偏心距对转动支撑统应力的影响分析

2020-04-13胡志华吴洪锦赵凌志

工程技术研究 2020年3期

崔斌，胡志华，吴洪锦，赵凌志

（中铁四局集团有限公司设计研究院，安徽合肥 230000）

近年来，在跨越既有铁路运营线的桥梁建设中，采用转体施工的工艺日益增多，尤其是平转体施工法。桥梁转体施工是在偏离桥位的位置，事先拼装或浇筑梁体之后借助转动装置将桥梁转动到设计轴线位置[1]。由于该方法可最大限度地减少施工对铁路运营线的影响，越来越受到工程建设者的青睐。

平转法施工中的转动支撑系统是整个转动体系的核心部分，主要由混凝土上转盘、下转盘和钢制球铰构成。在转体施工过程中，转动支撑系统的安全是转体施工成败的关键，因此支撑系统受力状态的研究十分必要。

在正载作用下转动支撑系统的受力研究较为常见，在偏载作用下的受力状态研究较少[2]。正载作用下，转动体重心和球铰中心重合，不存在偏心。然而实际工程中，由于梁体混凝土浇筑质量分布的差异，预应力张拉的偏差以及钢制球铰的制作和安装误差等因素，转体重量相对于球铰中心不可避免的存在一定的偏心[3-4]，而偏心会对球铰的受力状态产生不利影响，过大的偏心距会对转动支撑系统的安全造成巨大威胁。鉴于此，文章通过具体的工程案例采用有限元软件建立球铰接触模型，研究了转体偏心距对转动支撑系统应力的影响，并根据分析结果给出了解决建议和对策。

1 工程概况

某上跨铁路段高速公路T 构桥的孔跨布置为2m×60m，设计桥位线与铁路中线夹角为86°，工程施工时为减小对既有铁路运营的影响，采用转体法（平转法）施工。转体长度为56m+56m，两端各4m 梁段在转体完成后进行现浇。转体重量约1.5 万t。桥墩采用花瓶式实心矩形截面，墩高5.6m，墩底截面纵向长4m，横向宽13.5m。钢制球铰由上下两块钢球面板组成，球铰半径为10.0m，支撑半径为2.0m，钢板厚度为4cm。待转体就位后，上下转盘之间用C55 混凝土封固，共同形成桥梁的基础。

2 有限元模拟

采用有限元分析软件ANSYS 进行空间三维仿真分析，建立了球铰接触模型。该模型的核心就是要准确模拟上下钢制球铰球面间的接触受力行为。

球铰转动支撑系统采用中心支撑类型，转体重量由球铰承受，撑脚不与滑道接触。值得一提的是，文章仅研究偏心方向为桥梁纵向且转动体不平衡力矩小于球铰摩阻力矩的情况，即支架拆除后，球铰摩阻力矩能够克服转动体的不平衡力矩，转动体不发生刚体转动。模型中，桥墩只建立距墩底2m 高的范围，其余部分桥墩和桥梁上部结构以荷载形式施加在墩面；下转盘底面固结，桩基不建立。球铰模型单元和材料如表1 所示[5]。其中，CONTA174 单元的关键参数，除了KEYOPT（5）设置为自动调整接触状态，其余采用缺省设置[6]。

表1 有限元模型的单元和材料

当转动体不平衡偏心距e 为0 时，墩顶施加均布面荷载q，为式（1）；当转动体不平衡偏心距e 为不为0时，墩顶施加梯度面荷载，使面荷载合力大小为转动体自重G，合力作用点距墩中心纵向距离为e，如图1 所示。由此可得施加在墩截面的荷载值，为式（2）、式（3）。

式中：b 为墩截面横向尺寸；l 为墩截面纵向尺寸。

为了得到较好的计算精度，运用一定的网格划分技巧，该模型三维实体部分全部采用六面体映射网格。整个模型的单元划分结果如图2 所示。

图1 转动体考虑偏心距时自重的施加

图2 整个模型网格划分

3 不平衡偏心距的影响分析

当球铰摩阻力矩能克服转动体不平衡力矩时，转动体允许的最大偏心距emax按式（4）计算[7]。

式中：MZ为球铰摩阻力矩；μ 为球铰静摩擦系数；R 为球铰半径；其余参数同前。

计算可得emax=0.99m。

文章分别研究了转动体不平衡偏心距为0、0.15m、0.30m、0.45m、0.6m、0.75m 和0.9m 时转动支撑系统的最大压应力的变化规律，如图3 所示。

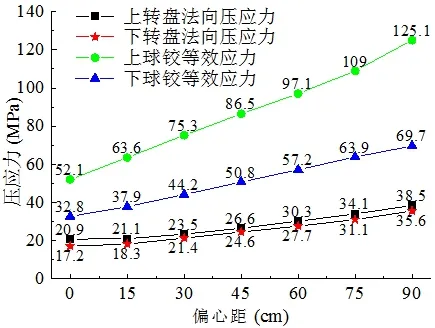
图3 偏心距对转动支撑系统受力的影响

由图3 可知，转动支撑系统的最大压应力随着偏心距的增大而增大；上下钢制球铰的应力水平明显高于上下混凝土转盘。该球铰钢材应力允许值为295MPa，偏心对钢制球铰的安全威胁较小。C55 混凝土的法向压应力允许值为24.85MPa，当偏心距达到36cm 时，上转盘压应力已经达到允许值，可见转动支撑系统的应力水平受上转盘控制。

偏心距为0 和30cm 时上转盘竖向应力云图如图4、图5 所示。由图4、图5 可知，当不存在偏心时，由于桥墩墩底截面为横向（图中Z 向）较长纵向（图中X 向）较短的矩形，上转盘压应力较大的位置偏横向一侧；随着纵向偏心的增加，上转盘压应力较大位置逐渐转向纵向一侧。图4 中，过转盘中心纵横建立两条路径X0、Z0；图5 中，过转盘中心纵向建立一条路径X30，上转盘竖向压应力沿路径的变化规律如图6 所示。可知，偏心距e=0 时，路径纵横向应力分布均对称于转盘中心，横向一侧最大压应力比纵向大5MPa 左右，且均在对应球铰支撑半径2m 的附近位置压应力出现峰值；纵向偏心距e=30cm 时，沿纵向路径，转盘应力呈现偏心侧应力大，远离偏心侧应力小的特点，同样在球铰支撑半径2m 的附近位置压应力出现峰值，左右两峰值应力差值达12.8MPa。若偏心的继续增大，上转盘混凝土的压应力在球铰支撑半径范围附近的分布更加不均匀，甚至会出现压应力集中在靠近偏心一侧，而远离偏心一侧的钢制上下球铰仅刚刚接触的现象，导致该侧上转盘应力非常小。如当偏心距为90cm 时，靠近和远离偏心侧的上转盘混凝土竖向压应力差值可达36MPa。

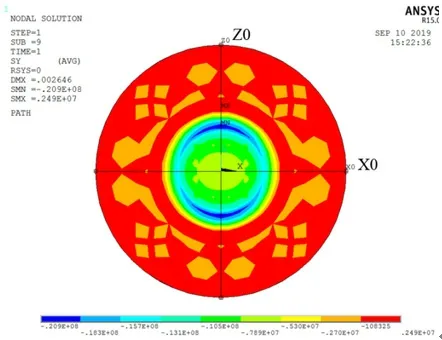
图4 偏心距为0 时上转盘竖向应力云图

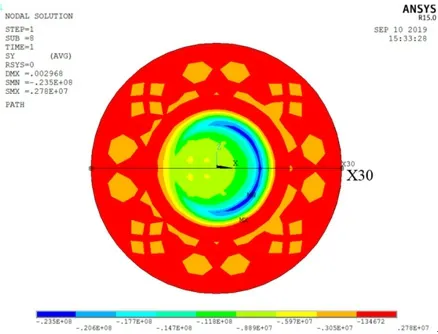
图5 偏心距为30cm 时上转盘竖向应力云图

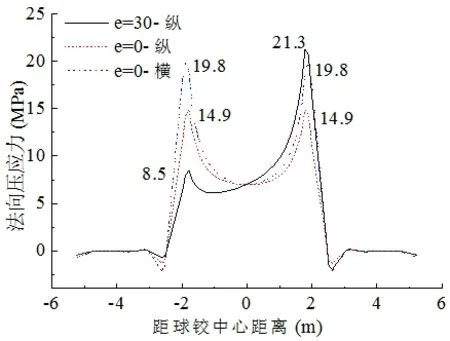
图6 上转盘竖向应力沿路径的变化规律

由以上分析可知，该转动支撑系统的应力水平受混凝土上转盘控制，且偏心距超过36cm 时，上转盘竖向压应力已超过限值；偏心距的存在会导致上转盘压应力分布不均匀，不能充分利用材料强度。按照常规的转体施工流程，在转体前应先拆除支架，拆除上下转盘间的临时支撑和临时锁定装置，转体重量也逐渐由球铰完全承担，随后进行梁体称重试验、梁体配重等后续工作。然而，在支架、临时支撑和锁定装置拆除后，梁体称重前，球铰已经承担了转动体自重荷载，此时并不知晓转动体的偏心距。若此时转动体的偏心距过大，上转盘混凝土应力已经超限，此种情况是十分危险的。若能在球铰完全承担转动体重量前预先得到不平衡力矩，并由此预先配重，即可保不平衡偏心距控制在合理的范围内，从而偏心距对转动支撑系统的安全威胁便可消除。

据相关文献，上述问题可由三维激光扫描仪进行解决[8]。三维激光扫描技术又被称为实景复制技术，可实现远距离高效、精准地采集目标表面的完整几何形态，完成对已浇筑梁段的轮廓识别和自重分析。本转体T 构桥分多次浇筑，从梁体第一次浇筑开始，可运用该技术对已浇筑的梁体进行扫描，获得悬臂两端已浇筑梁体重量，进而可知本阶段不平衡重，在下一梁端浇筑时进行针对性修正或预先配重。待梁体全部浇筑完成，再次扫描，获得最终不平衡重，由此便可在球铰完全承担转动体重量前把不平衡偏心距控制在15cm 的合理范围内[9]。