基于等效静态载荷法的平衡吊臂架结构优化

刘 宇，朱成章，尹 剑，马付建，杨大鹏，沙智华，张生芳

（大连交通大学机械工程学院，辽宁大连116028）

平衡吊是一种新型的高效节能的轻型起重设备，其运动主体为臂架构件。对于这种在动态系统中的结构部件而言，基于线性静态响应的结构优化结果往往无法满足实际工况的需求。20世纪90年代，Chol等［1-2］提出的等效静态载荷理论突破了以往动态优化领域局限于简单结构单自由度系统的不足，将动态系统所受载荷合理转化为等效的静态载荷，为平衡吊动态拓扑优化提供了理论基础。学者们成功地将该方法应用于高速机构的动态优化中，证明了该方法的有效性［3］。本文针对平衡吊动力学系统中臂架系统的外形结构，建立了平衡吊动态刚柔耦合模型，应用变密度方法，提出一种基于等效静态载荷法的系统级结构动态轻量化设计方法。

1 等效静态载荷原理

在线性静态分析中总存在某种载荷，可以替代运动结构所受动态载荷以产生与之相同的系统响应场。在动态载荷的作用下，结构表现最明显的一个特征就是动态载荷造成的位移。因此，可引入一个静态载荷，使物体在受该静态载荷作用下变形，形成的位移场与结构在承受某一动态载荷时的位移场相同，形成位移场等效，如图1所示。

图1 静态载荷等效过程Fig.1 Static load equivalent process

图1示意了静态载荷的等效过程。在规定的动力学分析中，总的计算时间步为n+1步，在等效时将每个计算时间步等效为静态分析的一个工况，并且要求由第Si个等效静态载荷计算得到的系统位移响应等价于对应时间节点的动态位移响应。因此，动力学分析中的总时间步数等于线性静态分析中的总工况数。在不考虑阻尼的情况下，动态载荷作用下物体结构的运动微分方程为

式中：M（b）为动态质量矩阵；K（b）为动态刚度矩阵；d（t）为位移矢量；f（t）为外部动态载荷向量。

根据有限元理论，在结构线性静态分析中存在如下表达式：

式中：feq为外部静态载荷向量；d为静态位移矢量。

根据位移场等效原理，在任意时刻t，等效静态载荷将使物体产生与受到动态载荷作用相同的位移场，即

式中：KL（b）为在线性静态分析中物体结构刚度矩阵。在任一时刻，对于任意一个动态载荷都存在一个与之相对应的等效静态载荷。即t=ti等价于s=si，对应得到n组等效静态载荷。

由式（2）和式（3）可知，通过结构线性静态分析，得到的静态位移矢量等于其对应时刻节点非线性动态位移矢量。即当等效静态载荷作为外力施加于结构线性静态优化中时，静态线性的位移场响应与动态非线性的位移场响应相同。且据有限元理论，应力通过节点位移计算得到，因此，相同的位移场也会产生相同的应力场。

2 结构动态拓扑优化技术及设计过程

2.1 拓扑优化方法

源于均匀化方法的变密度法是目前在连续体结构拓扑优化领域应用最广、影响最深的一种优化方法［4］。通过人为设定材料宏观物理参数，变密度法把连续体结构离散成有限元模型，并将每个单元的密度定义为设计变量，可在0（无实体的空集）和1（实固体）之间变化，其本质是为了找寻最佳的材料分布。

由于产生中间密度而导致优化结果出现的棋盘格现象，将使优化结果不尽人意。因此，必须引入某种惩罚因子，尽可能消除中间密度区域并迫使最终的设计变量值为 0或1［5］：

2.2 动态拓扑优化流程

对平衡吊臂架系统结构进行动态拓扑优化设计，需要以动力学模型为基础。在优化过程中，可将通过分析得到的动态载荷作为结构优化模型的载荷边界条件。其结构动态优化设计步骤如下：

步骤1设置动态载荷工况，对平衡吊臂架系统模型进行动力学仿真。

步骤2根据式（1）计算仿真时间段内所有时间间隔内的位移场，再利用位移场等效原理，根据式（2）分别计算对应时间间隔内的等效静态载荷。

步骤3按照时间步将等效静态载荷（Equivalent Static Loads，ESL）转变为多工况外部载荷，将ESL作为多重载荷条件应用于优化过程。

步骤4求解静态线性响应问题，不断重复这个过程直到满足收敛条件‖ ‖bk-bk-1≤ε，ε为收敛误差范围参数。

其中，步骤4求解线性响应方程如下：

式中：k为循环系数；gj为优化问题的约束函数。

3 平衡吊臂架系统动态优化

3.1 仿真模型建立

研究对象为平衡吊臂架系统，主要包括大横臂、小横臂、吊重臂、连杆、滚轮、台架等部件，主要结构如图2所示。本文针对平衡吊四连杆臂架系统进行优化，其余部件仅用于传递载荷及导向。平衡吊设计为可吊起1 000 kg的重物，在此针对平衡吊两个典型工况分别进行分析［6］。当吊钩处挂起1 000 kg重物后：①垂直运动，固定滚轮C，在驱动杆上（即ABD杆的A端）施加竖直方向匀速驱动，模拟吊钩上提重物过程；②水平运动，驱动杆固定，在F点处施加水平方向匀速驱动，模拟手推吊钩迫使C点的滚轮沿槽水平运动。

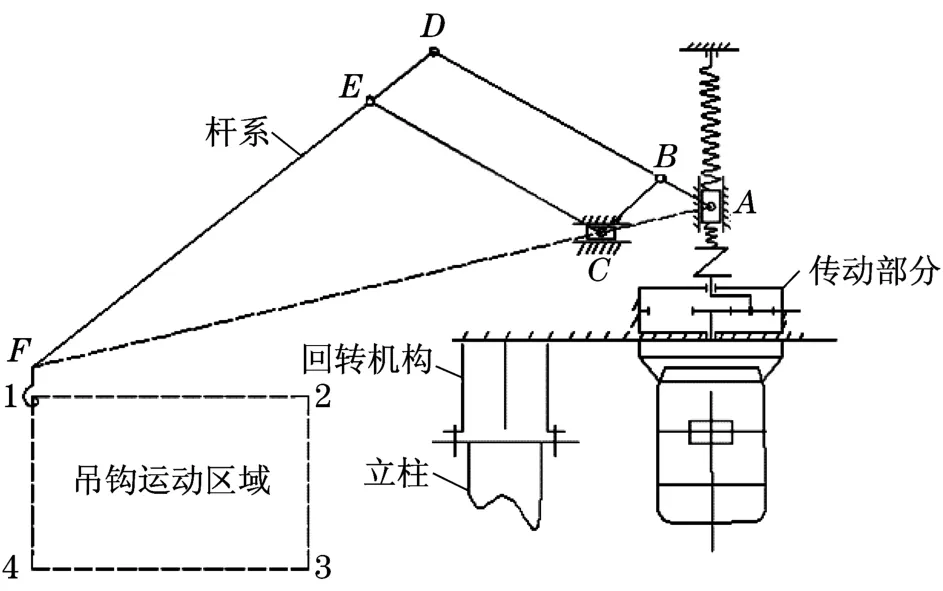
图2 平衡吊结构原理图Fig.2 Schematic diagram of balanced crane structure

其余部分关键部件运动关节设置如表1所示。

表1 刚柔耦合模型中各部件间的约束关系Tab.1 Constraints between components in a rigidflexible coupling model

用计算机工程应用软件Creo建立平衡吊系统三维模型，并导入Hypermesh中进行有限元前处理，臂架系统均采用四面体网格结构，去除原模型中不影响分析的细小结构以便于有限元网格划分。四连杆臂架系统材质选用Q345B结构钢，其抗拉强度σb≤490 MPa，条件屈服强度σ0.2≤345 MPa，弹性模量E=2.06×1011N/m2，泊松比 0.25，密度 ρ=7 850 kg/m3。在有限元分析基础上，采用CMS模态综合技术将大横臂、小横臂、吊重臂、连杆转化为多体动力学中的柔性体，并保留前20阶非刚体模态，其余部件作为刚性体处理，前处理后平衡吊动力学模型如图3所示。

图3 平衡吊有限元模型Fig.3 Balanced crane finite element model

图4 骨架系统应力云图Fig.4 Skeleton system stress cloud diagram

3.2 动力学仿真结构

通过对平衡吊系统在两种工况下的运动仿真，可得到各个连接部件之间作用的动态载荷以及在载荷作用下结构的动态应力。平衡吊从初始位置抬起到最高点用时20 s，从作业范围最外侧移动到最内侧用时20 s。设定两种工况仿真计算时间为20 s，步长0.1 s。取5，10，15和20 s时间节点等效应力，如图4所示，两种工况下最大动态应力均出现在ABD杆上。平衡吊臂架系统在垂直仿真时段内最大动态应力出现在0.20～0.25 s之间的峰值处，该值为246.3 MPa，如图5（a）所示；在水平运动仿真时段内最大动态应力出现在0.20～0.25 s之间的峰值处，该值为215.1 MPa，如图5（b）所示。

图5 臂架系统最大应力曲线Fig.5 Maximum stress curve of boom system

3.3 动态优化设计的数学模型

应变能是以应变和应力的形式贮存在物体中的势能。在有限元理论中，单元应变能公式为

式中：B为应变矩阵；D为弹性矩阵；｛δi｝为单元位移矩阵。

由于单元矩阵

所以单元应变能公式又可以这样表述：

式中：K为刚度矩阵；U为单元节点位移矩阵。

因此，可以将应变能作为结构刚度的评价指标，应变能越小刚度越大。结构应变能最小的拓扑优化设计数学模型建立如下：

式中：P为变密度法定义的单元相对密度矢量；Δ为质量分数最大值；ρmin为单元相对密度最小值。

在变密度法中，材料密度处于［0，1］分布，由于ρi=0时，代表单元无材料，对应单元刚度矩阵为0，将导致结构刚度矩阵奇异，难以求解。因此，引入ρmin代替ρ≤ρmin的单元，代表该单元处没有材料，而这些单元刚度值极小，代替后对整体运算精度影响不大。

3.4 结构动态拓扑优化结果及分析

为了满足平衡吊动态特性，以平衡吊机构最大应变能最小为目标函数，以机构质量为约束条件，建立优化区域动态优化设计模型，即在机构应力变化不超过允许值的情况下，对平衡吊四连杆臂架系统同时进行动态优化，避免单独优化各杆件时相互间承受载荷的变化对优化结果的干扰。在优化设计时采用的质量约束仅运用到包含设计空间的模型部分，以此来控制其优化结果的材料保留量。质量约束为0.8（优化结果保留材料不超过原材料的80%）时，两种工况下平衡吊臂架系统优化结果如图6所示。

分析结构动态拓扑优化结果，平衡吊垂直运动与水平运动条件下，得到的杆件优化构型具有相似性。究其本质，是因为在动力学仿真时，两种工况下的臂架系统最大应力曲线有相似的走势，此时根据等效静态载荷原理，得到的臂架系统等效静态载荷也具有相似的变化趋势，而作为动态优化的边界条件，等效静态载荷将对优化结果起到至关重要的影响。从结果中可以看出：ABD杆外部左右两侧在厚度方向上被去除了部分材料，且主要变化区域为杆件底侧，顶侧由于需要承载大部分拉应力而得到保留；BC杆作为与滚轮相连的结构杆件，其大体形状被保留，最外围轮廓部分材料由于对结构承载贡献不大而被去除；CE杆在平衡吊工作时主要承载压应力，其优化结果的外轮廓更趋近于圆柱体；DEF杆内部在杆件长度方向形成通孔，外轮廓类似于ABD杆在左右两侧被去除了少部分材料。垂直运动、水平运动工况下平衡吊优化前后臂架系统各杆件参数对比分别如表2和表3所示。

图6 结构动态拓扑优化结果Fig.6 Structural dynamic topology optimization results

表2 垂直运动工况下的结构动态优化结果Tab.2 Results of dynamic optimization of structuresunder vertical motion conditions

表3 水平运动工况下的结构动态优化结果Tab.3 Results of dynamic optimization of structuresunder horizontal motion conditions

从表2和表3中的数据对比可以得出：在平衡吊垂直运动与水平运动两种工况中，优化后的臂架系统各杆质量均有一定程度的减小。垂直运动工况中，ABD杆质量减少了20.38%，BC杆质量减少了25.24%，CE杆质量减少了22.57%，DEF杆质量减少了21.55%；水平运动工况中，ABD杆质量减少了23.68%，BC杆质量减少了23.27%，CE杆质量减少了30.33%，DEF杆质量减少了26.41%。优化后的最大应力与优化前相比均稍有增大，这是因为在优化过程中，由于存在质量分数的约束限制，臂架系统各杆件均因去除部分材料而降低了刚度，即便如此，平衡吊臂架系统优化后的各杆应力最大值均远小于材料屈服强度345 MPa。

4 平衡吊臂架系统轻量化设计

4.1 动态优化结果重构

结合两种工况下平衡吊动态拓扑优化的结果，给出一种平衡吊臂架系统的重构方案。平衡吊各杆件重构模型如图7所示，该方案加强了各杆件在关键传力部位的结构，基本继承了动态拓扑优化的结果构型，并考虑的各杆件在工程中的实际可制造性。

图7 平衡吊重构模型Fig.7 Reconstruction model of balance crane

对重构模型进行动态应力分析，网格划分采用四面体结构，设定基本参数、仿真时间、步长与原结构动力学仿真一致，得到平衡吊臂架系统优化后最大应力变化曲线，此时最大应力仍出现在ABD杆上，如图8所示。

图8 优化后臂架系统最大应力曲线Fig.8 Optimize the maximum stress curve of the rear boom system

两种工况下的重构结构分析结果对比如表4所示。

表4 水平运动工况下的结构动态优化结果Tab.4 Structural dynamic optimization results under horizontal motion conditions

重构后的臂架系统各杆件质量均有一定程度的减小：ABD杆质量减少了26.90%，BC杆质量减少了28.57%，CE杆质量减少了17.62%，DEF杆质量减少了38.67%。重构后的最大应力与优化前相比均稍有增大，但各杆应力最大值均远小于材料屈服强度345 MPa，满足平衡吊设计要求。

5 结论

本文针对平衡吊动力学系统中臂架系统的外形结构，建立了平衡吊动态刚柔耦合模型，并应用等效移动载荷法，提出一种基于等效静态载荷法的系统级结构动态轻量化设计方法，所得结论如下：①通过等效静态载荷法将非线性多体动力学分析与线性静态结构优化相结合，可以实现大型结构系统级动态拓扑优化；②采用等效静态载荷法对平衡吊臂架系统结构进行轻量化设计，需综合考虑多个工况下的动力学分析结果。本文根据不同工况下平衡吊臂架系统的承载规律以及不同工况下的动态优化结果，给出了一种平衡吊臂架系统构型方案。该方案在满足各杆结构强度的前提下，各杆质量均有较大幅度减小，为平衡吊臂架系统结构设计提供了参考。