矿井救援车提升吊臂挠度变形与变幅补偿研究
2022-07-27朱文锋顾海荣刘庆修田宏亮
朱文锋,顾海荣,刘庆修,田宏亮
(1.长安大学工程机械学院,陕西 西安 710064;2.中煤科工集团西安研究院有限公司,陕西 西安 710065)
1 引言
钻孔救援技术作为矿山应急救援的一项有效实用的救援技术,通常为事故发生后开凿钻孔救援,智利矿难、平邑石膏矿事故等均采用此技术成功实现救援[1]。救援井是安设在避险空间内直通地面的大孔径钻孔,为井下遇险人员的快速撤离提供通道。矿井救援车,如图1所示。可通过救援井将救援舱放至井下,实现遇险人员的提升救援。

图1 矿井救援车Fig.1 Mine Rescue Vehicle
在矿井救援的过程中,稳定提升是救援的关键。但是在实际救援过程中,由于提升吊臂的挠度变形,会造成救援舱在救援井内偏离中心轨道,救援舱会与救援井壁发生碰撞摩擦,对井壁与舱壁造成破坏,影响提升的稳定性,更可能造成被困人员的二次伤害,因此获取提升吊臂精确的变形量,然后通过变幅系统进行补偿,成为了确保提升稳定性的关键。
矿井救援车是在汽车起重机的基础上研究而来,提升吊臂挠度的变形研究有相似之处。文献[2-6]利用二阶理论,推导了箱型伸缩臂的刚度矩阵,利用刚度矩阵求解提升吊臂的挠度变形,但是计算量较大,过程繁琐。文献[7]认为提升吊臂内的伸缩缸承受轴向力,利用微分方程推导了吊臂的变形和欧拉临界力。但是目前的提升吊臂内的伸缩缸只是起到了伸缩的动作,达到伸出长度后各个臂节之间多用挡块或插销固定,伸缩缸不受轴向力,所以此模型不太适用。文献[8]利用ANSYS软件对QY25K型汽车起重机伸缩式吊臂进行静力学分析,求解了在自重、风载等作用下吊臂末端位移并与实验结果作对比,证明了建立的有限元模型与实际情况比较接近。但是这种变形分析计算方法只能根据特定模型得到变形的数值解,得不到变形公式。文献[9-10]研究出适用于底部弹性支撑和承受轴向力的阶梯柱的稳定性分析方法,并给出了精确解析解,可以计算出变形量。文献[11]研究了阶梯梁的横向扭转屈曲抗力,通过引入系数提出了新的横向屈曲公式。文献[12]研究了钢丝绳对吊臂动态特性的影响,采用模态叠加瞬态动力学分析法研究了不同载荷频率对吊臂最大应力的影响。
以ZMK5200QJY40 型矿用救援车为研究对象,通过理论分析,推导静态时吊臂挠度表达式。通过仿真分析,验证理论表达式的正确性,并进一步分析吊臂挠度变形与吊重、吊臂长度以及变幅角度的关系,为精确变幅补偿和提升稳定性提供理论指导。
2 基于非线性理论的吊臂挠度变形
矿井救援车提升吊臂简化结构模型,如图2所示。为了分析方便,将结构模型进一步简化的力学模型,如图3 所示。如图3(a)所示,以变幅液压缸的上铰点为分割点,将挠度的理论推导分为两部分:第一部分是吊臂OA段与变幅液压缸组成的两端铰支撑的压弯梁,第二部分是吊臂A点往上的弹性支撑悬臂梁;两者相互关联密不可分。假设变幅液压缸的刚度无穷大,不发生弹性变形,则提升吊臂底部OA段和变幅液压缸可以等效为图3(b)所示的弹性支撑,提升吊臂的转动刚度正是等效后悬臂梁根部弹性支撑刚度。

图2 提升吊臂结构简图Fig.2 Structure Diagram of Telescopic Boom
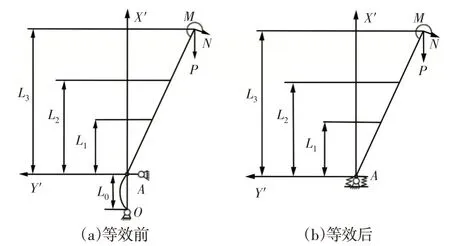
图3 提升吊臂两铰支撑的等效处理Fig.3 Equivalent Treatment of Two Hinged Support of Telescopic Boom
2.1 吊臂底部等效弹性支承刚度推导与验证
2.1.1 弹性支承刚度推导
等效模型,如图4所示。提升吊臂上部的载荷可以等效为作用在A点的弯矩MA和轴向力P。以提升2t为例,轴向力P=52418.11N,弹性模量E=2.06E+11Pa,惯性矩I1=2.05E-4m4,OA长度L0=0.7m。
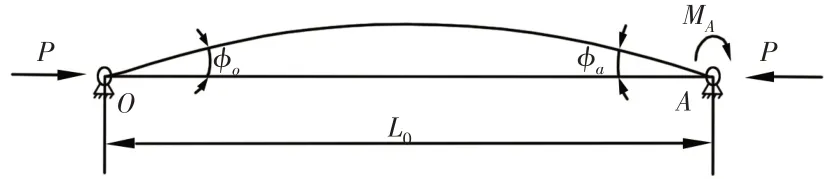
图4 提升吊臂底部弯曲变形Fig.4 Bending Deformation at the Bottom of Telescopic Boom
在弯曲状态下,考虑轴向力与弯矩的作用,根据纵横弯曲理论,梁的弯矩与转角的关系有[4]:

式中:E—材料杨氏弹性模量,Pa;I1—基本臂截面惯性矩,m4;L0—提升吊臂底部OA段长度,m。
2.1.2 弹性支承刚度验证
TIMOSHENKO S P 给出了长度为l的两端铰接压弯柱在一端受力矩为M、轴向力为P时的柱端转角计算公式:

根据转动刚度计算公式,对应的转动刚度为:

利用两种方法计算,提升吊臂的转动刚度均为CA=1.81E+08N·m/rad,证明上述推导正确。
2.2 提升吊臂末端挠度变形的推导
设末端挠度为Y,对提升吊臂建立挠曲微分方程:

式中:Ii—提升吊臂第i节臂截面惯性矩,m4;Li—提升吊臂第i节臂端部到A点距离,m;x—提升吊臂上端悬臂梁的长度,m;yi—提升吊臂上端悬臂梁长为x处的挠度,m。
求解上式可得,通解为:

整理可得,式(8)中的系数An,Bn可由以下递推式表示:
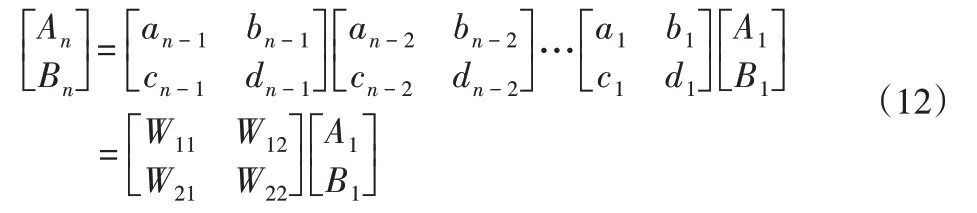
(3)已知条件x=Ln,yn=Y,得:

式(16)便是静态时考虑二阶效应的变截面悬臂梁端部挠度变形的精确表达,其中,CA是第一部分的转动刚度,可见,挠度变形量与转动刚度密切相关,此表达式可以计算静态时吊臂挠度的变化值。当N、M分别取为单位力时,1/Y即为侧向刚度,式中系数αn、βn是关于节数n的递推公式。
3 吊臂挠度变形算法对比分析
3.1 基于线性理论的吊臂挠度变形
常用的吊臂挠度变形的理论计算方法还有基于材料力学的线性计算法,为了与前述非线性理论算法进行对比,现列出吊臂挠度变形的线性计算法。该算法基于虚功原理,其计算公式为:

式中:ξ—某一修正系数;k—吊臂的节数;Ln—末节臂端部到支撑点A的距离,m;u0=L0/Lb,ui=(L0+L)i/Lb—长度系数;Lb—吊臂总长,m。
3.2 基于仿真的吊臂挠度变形
以ZMK5200QJY40型矿用救援车为研究对象,在臂长10m、变幅角度60°的基础上,对不同的起吊重量进行有限元仿真分析。已知救援车的吊臂结构特性参数,如表1所示。

表1 ZMK5200QJY40型矿用救援车吊臂结构特性参数Tab.1 Structural Parameters of Telescopic Boom of ZMK5200QJY40 Mine Rescue Vehicle
利用有限元软件ANSYS Workbench对矿井救援车提升吊臂模型进行仿真分析,通过划分网格、约束处理与载荷施加获取分析结果,臂长10m,变幅角度60°,起吊重量2t时,提升吊臂的变形量仿真结果,如图5所示。
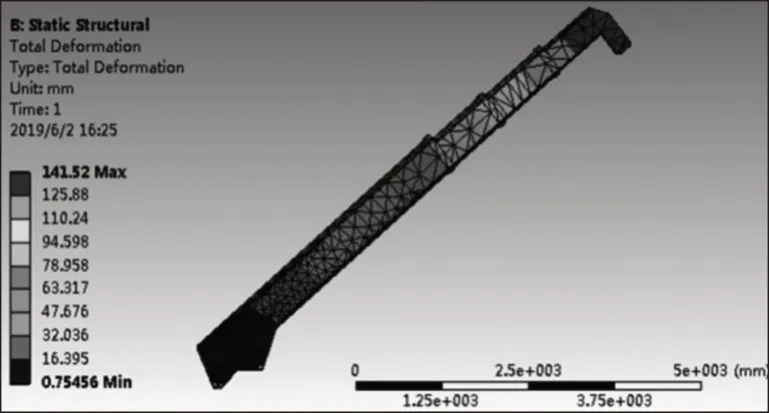
图5 提升吊臂挠度变形仿真Fig.5 Simulation of Deflection Deformation of Telescopic Boom
将两种理论计算结果和仿真结果进行对比,如表2所示。可以发现,采用非线性理论计算的挠度与仿真结果的误差在3%以内,误差较小。采用线性理论计算的挠度总体偏小,原因是该方法忽略了轴向力对吊臂挠度的影响,符合实际情况。

表2 吊臂挠度变形计算与仿真结果Tab.2 Calculation and Simulation Results of Deflection Deformation of Telescopic Boom
将计算结果用图曲线表示,如图6所示。可以发现三种算法的吊臂末端挠度均与吊重近似成正比,非线性解更加接近仿真解,证明了非线性理论计算模型的正确性。
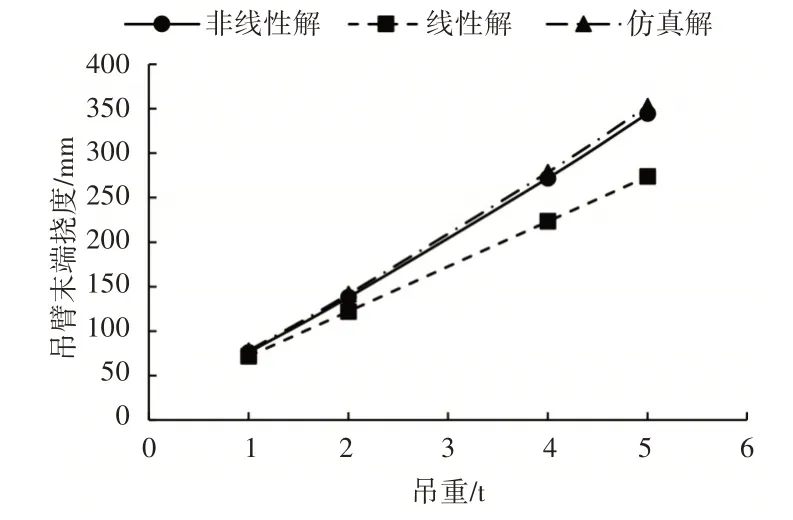
图6 不同算法吊臂挠度变形对比Fig.6 Comparison of Deflection Deformation of Telescopic Boom with Different Algorithms
4 提升吊臂挠度变形分析
根据前面的分析可知,提升吊臂挠度变形与吊重存在近似正比关系,提升吊重的增加,直接影响吊臂的受力,吊臂变形量随提升吊重的增加而增加,成近似线性关系。
进一步研究吊臂挠度变形量与吊臂伸长量和变幅角度的关系。
取吊重为2t,利用挠度计算公式对不同吊臂伸长量、不同变幅角度的情况计算挠度变形量,计算结果,如图7所示。
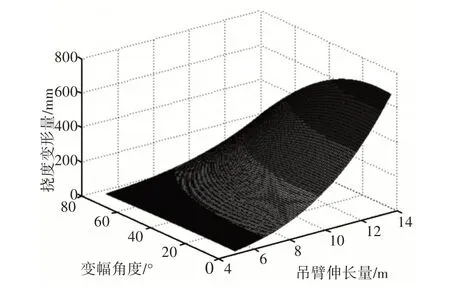
图7 挠度变形三维图Fig.7 Three-Dimensional Diagram of Deflection Deformation
在图中一个区域是提升的安全区域,救援车在此区域内以任何姿态提升,吊臂挠度变形都会小于53mm,吊臂水平位移小于46mm,救援过程中可以有效避免摩擦;在安全区域内吊臂在最小变幅角度时,伸长量只能达到6.5m;吊臂在最大变幅角度75°时,伸长量能达到9.9m。随着颜色的加深,变形量不断增大,颜色最深的部分变形量都在600mm以上,如果此时姿态提升,将会对井壁与舱壁造成严重的磨损破坏。在最大伸长量13.6m、变幅角度为7°时变形量最大,达到691.34mm。
变幅角度是矿井救援车姿态的重要参数,变幅角度对吊臂挠度的影响,如图8所示。变幅角度与变形量成负相关的关系,变幅角度越大,变形量越小。
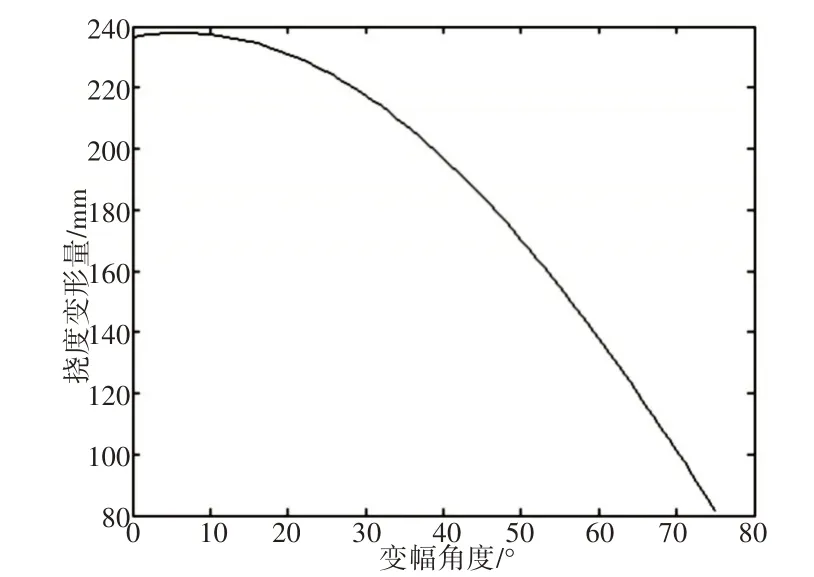
图8 挠度变形随变幅角度的变化Fig.8 Change of Deflection Deformation with Lifting Angle
变幅角度增大,吊臂上的切向力减小、轴向力增大,增加了吊臂的刚度,吊臂的变形量变小。由图可以看出最大变形量并不是在0°的时候,而是在7°附近,此时吊臂受力最大。
吊臂伸长量与挠度变形量的关系,如图9所示。随着吊臂的不断伸长,变形量呈增加趋势,且吊臂越来越长时,变形量增加的速率也在增大。吊臂的伸长与缩短,影响着挠度计算系数α、β,所以吊臂的变形量会发生变化。
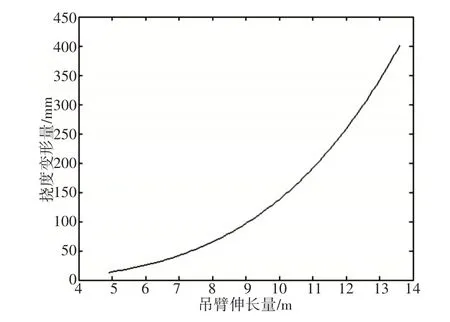
图9 挠度变形随吊臂伸长量的变化Fig.9 Change of Deflection Deformation with Boom Length
5 矿井救援车变幅补偿分析
矿井救援车的变幅补偿的工作原理,如图10所示。在理想情况下,矿井救援车提升吊臂处于OA状态,钢丝绳和吊舱沿着AD垂直向下。但在实际情况下,由于钢丝绳和吊舱的重力作用,吊臂处于OB状态,吊舱的工作幅度由R前变为R后。另外,救援井的深度达到几百米,钢丝绳在上升和下方过程中,自重的变化会大大影响提升吊臂末端的挠度变形,且救援井的直径有限,因此为了避免救援仓与救援井壁的碰撞,在救援仓提升或下方过程中,需要实时改变提升吊臂的变幅角度,即实时改变变幅油缸的伸缩长度,以补偿吊重的改变引起的挠度变形。当吊臂长度一定时,工作幅度与吊臂挠度变形量、变幅角度有关,且吊臂挠度变形量也与变幅角度也有关,因此直接求解吊臂的修正变幅角度非常困难。可采用线搜索的方法,选取适当的搜索步长和搜索方向,通过迭代算法求解最优的变幅角度。

图10 矿井救援车变幅补偿原理图Fig.10 Schematic Diagram of Luffing Compensation About Mine Rescue Vehicle
依托矿井救援项目,救援井的直径为606mm,救援舱的直径为560mm,救援井与救援舱的水平间隙为46mm。取变幅角度为60°,计算不同臂长和吊重工况下吊臂的挠度变形量,如表3 所示。吊臂水平位移小于46mm时,对应的挠度变形应小于53mm,救援过程中救援仓和井壁就不会发生碰撞摩擦,因此可以在表中画出安全提升的分界线。在伸缩臂全缩的状态下,即臂长4.9m,提升重量不超过8.6t,可以安全提升;当臂长10m时,提升重量超过1t,需要进行变幅补偿;在伸缩臂全伸的状态下,即13.6m,由于变形量较大,在任何起重量情况下都需要进行变幅补偿。
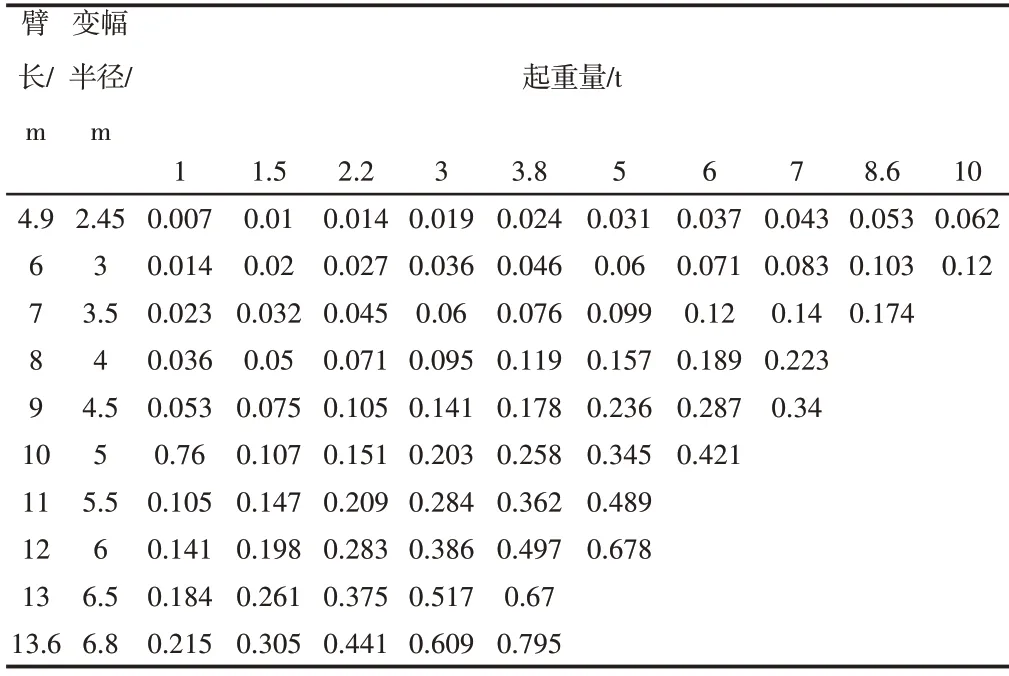
表3 提升吊臂挠度变形表Tab.3 Deflection Deformation Table of Telescopic Boom
6 结论
对矿井救援车伸缩式提升吊臂的受力模型进行合理等效,得到了任意节臂数的提升吊臂挠度变形量理论计算公式。针对ZMK5200QJY40型矿井救援车,通过理论计算和有限元仿真,得到如下结论:
(1)利用非线性微分方程理论计算的吊臂挠度和仿真的结果非常接近,误差小于3%,低于工程应用的允许范围,验证了这里建立的模型与推导的挠度变形计算公式的正确性,利用此公式计算吊臂挠度可以节约建模与仿真时间,为高精度变幅补偿提供支持。
(2)分析吊臂变形的影响参数,得出挠度随之变化曲线。吊臂挠度变形量随提升吊重的增加而线性增加;吊臂挠度随提升吊臂的长度的增加而增加,且吊臂越长,变形量增加的速率越大。吊臂挠度随变幅角度的增加先增加,在7°附件达到最大值,然后随着变幅角度的增加而减小。
(3)阐述了矿井救援车变幅补偿的原理,通过实时改变提升吊臂的变幅角度,即实时改变变幅油缸的伸缩长度,以补偿吊重的改变引起的挠度变形。
(4)在变幅角度60°的基础上,对不同吊臂长度、不同吊重工况下吊臂的挠度变形量进行了计算,绘制了挠度变形表,方便观察不同工况的变形量情况,并标注了安全提升区域,方便工程人员参考与查阅。
