基于整体稳定性的全地面起重机偏心调整架与超起装置的相互关系

姚峰林，石国善，孟文俊，白艳强，崔耀东

（太原科技大学机械工程学院，山西太原030024）

随着全球范围内大型工程项目的建设，在要求起重机满足大起重量的同时，又要满足超高的起升高度和超大的作业半径，因此，主臂和副臂的组合方式被广泛采用［1-2］，诞生出形式多样的臂架组合系统，其中塔式副臂超起组合臂架系统是最典型的一种组合工况。起重机在工作时，组合臂架系统承受自重、吊载、偏载、风载以及起升绳力的耦合作用［3］。当塔式副臂组合臂架较长时，由于材料强度高、结构截面小、长细比较大、相对强度破坏，臂架的稳定性成为决定其起重性能的关键因素［4-5］。为改善全地面起重机在超高空作业时臂架系统的受力情况，提高臂架系统的整体稳定性，在主臂、副臂连接架处分别安装超起装置和偏心调整架。杨玉姣［6］分析了偏心调整架参数对伸缩臂系统各构件受力的影响。本文以500 t全地面起重机塔式副臂超起组合臂架系统为研究对象，其三维模型如图1所示。

图1 全地面起重机塔式副臂超起工况三维模型Fig.1 3D model of all-terrain crane with tower jib

1 组合臂架系统的有限元模型

结合全地面起重机塔式副臂超起组合臂架系统中各部件的受力形式，为其选择合适的单元进行模拟。七节伸缩主臂、塔式副臂、连接架、超起撑杆、偏心调整架及塔式副臂前后撑杆均采用BEAM188单元模拟，伸缩臂的截面采用PLANE82单元进行网格划分，超起拉板及钢丝绳采用LINK180单元模拟，采用节点自由度耦合技术来模拟滑块与各节臂的接触［7］。分析工况：主臂长78.6 m，主臂仰角83°，塔式副臂长21 m，副臂仰角48.4°，超起撑杆张开角度α1=90°，超起撑杆变幅角度 α2=90°，超起撑杆长度L1=10.95 m，偏心调整架撑杆张开角度θ1=80°，偏心调整架撑杆变幅角度θ2=100°，偏心调整架撑杆长度L0=5.5 m。超起装置及偏心调整架的关键参数如图2所示。

图2 关键参数Fig.2 Key parameters

组合臂架系统的材料属性如表1所示，承载情况如表2所示。表2中，PG0为臂架系统的自重；PQ0为吊载；φ1为冲击系数；φ2为起升动载系数；C为风力系数；Kh为风力高度变化系数；β为风振系数；P为计算风压；A为迎风面积；γ为货物偏摆角；m为起升滑轮组的倍率；η为起升滑轮组的效率［8］。

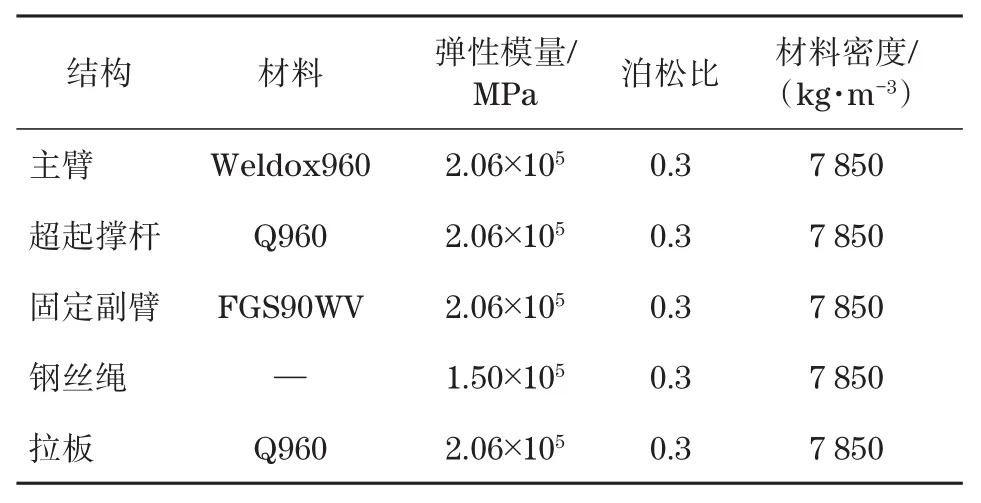
表1 组合臂架系统的材料属性Fig.1 Material properties of combined boom system

表2 组合臂架系统的承载情况Fig.2 Load condition of combined boom system

根据以上信息，建立塔式副臂超起组合臂架系统的有限元模型，如图3所示。

2 组合臂架系统的屈曲分析

2.1 特征值屈曲分析

特征值屈曲分析方法由最小势能原理推出，运用有限元的离散思想，可得结构体系的总势能表达式为

式中：K为结构的整体刚度矩阵；F为节点所受的载荷；u为结构的节点位移。

由最小势能原理知，对于任何平衡状态，必须满足总势能的一阶变分为零的条件［3，9］，由此可得结构的平衡方程为

式中：结构的整体刚度矩阵K等于结构的弹性刚度矩阵KE与结构的几何刚度矩阵（又称初应力矩阵）KG之和，即K=KE+KG。

特征值屈曲分析是建立在小变形线弹性理论基础上的，在这种假设下，在结构为屈曲时材料处于弹性状态，载荷F与初应力刚度矩阵KG具有相同的线性关系。故若对结构施加载荷F0，结构的初应力刚度矩阵为KG0，当施加载荷F=λF0时，结构的初应力刚度矩阵为KG=λKG0，此时结构的平衡方程为

当外载荷F达到屈曲临界点时，结构处于随遇平衡状态，此时载荷不发生变化，但是结构会转到与其原有平衡状态相邻的平衡状态，平衡位形u变为u+Δu，此时结构的平衡方程为

式（4）减式（3），得

式中：λ为载荷乘子（也称为载荷因子或特征值）；Δu为结构发生屈曲时的屈曲模态。

式（5）的形式与线性代数中的Aα=λα相同，故可将其归为求解特征值的问题，为了使式（5）有非平凡解，需要满足

即结构的切线刚度矩阵为奇异矩阵。

使用ANSYS软件对第1小节建立的有限元模型进行特征值屈曲分析，得到塔式副臂超起组合臂架系统的临界吊载为90.2 t。其前6阶载荷因子如表3所示。

表3 特征值屈曲分析前6阶载荷因子Fig.3 The first 6 order load factors of eigenvalue buckling analysis

表3中前两阶特征值（载荷因子）均为负值，从第3阶开始往后变为正的特征值。负的特征值表明当所有施加在结构上的载荷反向时结构会发生屈曲，如果所分析的对象不会出现载荷同时反向的情况，则可以忽略负的特征值。取第3阶、第4阶屈曲模态如图4所示。

图4 特征值屈曲分析第3和第4阶屈曲模态Fig.4 The third and fourth order buckling mode of eigenvalue buckling analysis

2.2 几何非线性屈曲分析

非线性屈曲分析是基于大变形理论的，此时载荷F与节点位移u呈非线性关系，结构体系的本构方程［3］可表述为

式中：KT为结构的切线刚度矩阵，KT=KE+KG+KL，KL为基于大变形的初位移矩阵。

根据特征值屈曲分析得到的结果，引入初始几何缺陷，即载荷因子逼近1时为结构形变的0.01倍，以臂架头部节点N207作为目标节点，设定力、力矩收敛准则，采用弧长法对模型进行非线性屈曲分析，得到模型对应的载荷-位移曲线，如图5所示。由载荷-位移曲线可知，当吊载Q为60.04 t（即588.39 kN）时，臂架头部节点N207在UX，UY，UZ3个方向上的载荷-位移曲线出现极值点，故认为非线性屈曲分析的临界屈曲载荷为60.04 t。

图5 非线性屈曲分析的载荷-位移曲线Fig.5 Load-displacement curve of nonlinear buckling analysis

3 偏心调整架与超起装置的关系

在本小节的分析中，分析工况为：主臂长78.6 m，主臂仰角83°，塔式副臂21 m，副臂仰角48.4°，采用特征值屈曲分析方法进行研究。

3.1 L0与L1的关系

保持θ1=80°，θ2=100°，α1=90°，α2=90°不变，改变L1，得到不同L1条件下L0对塔式副臂超起组合臂架系统整体稳定性的影响曲线，如图6所示。由图6可见，对不同的L1，组合臂架系统的整体稳定性随着L0的增大先增强后减弱，且随着L1在［5 m，16 m］区间内的增大，相同L0对应的臂架系统的整体稳定性逐渐增强，且变化幅度减小。

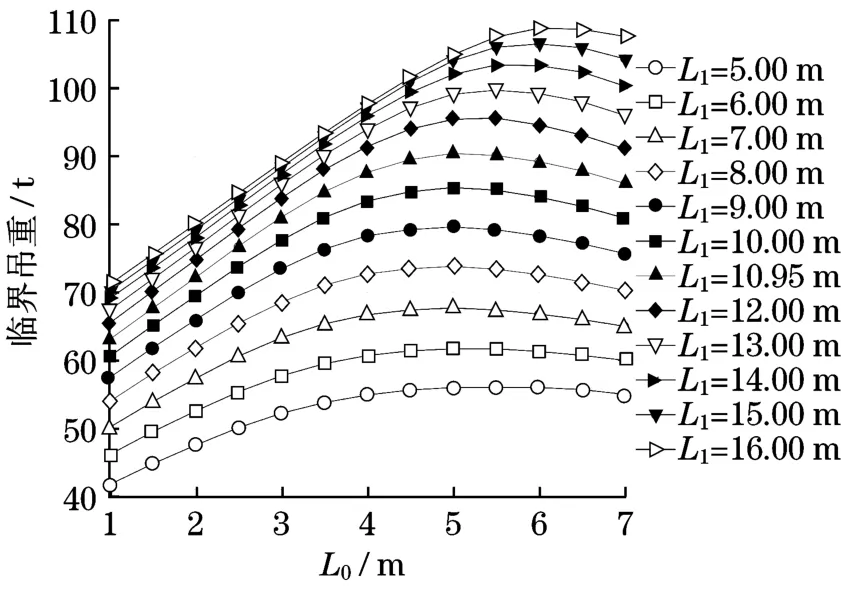
图6 不同L1对应的L0的影响曲线Fig.6 Influence curve of L0corresponding to different L1

绘制L0与L1的相互关系的等值线图，如图7所示。为使组合臂架系统达到最佳的稳定状态，如图7中的黑色实线所示，L0随L1的增大先减小后增大。如图7中的黑色虚线所示，L1随L0的增大保持不变，L1稳定在16 m。

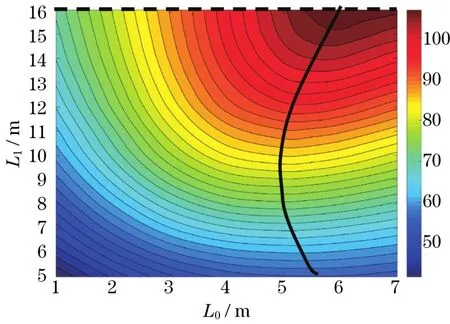
图7 L0与L1的相互关系的等值线图Fig.7 Isogram of the correlation between L0and L1

绘制L0与L1的相互关系的3D图，如图8所示。

3.2 θ1与α1的关系

保持L0=5 m，θ2=100°，L1=10.95 m，α2=90°不变，改变α1，得到不同α1时θ1对塔式副臂超起组合臂架系统整体稳定性的影响曲线，如图9所示。由图9可知，随着α1由20°增加到160°，关于θ1的影响曲线的峰值逐渐向左移动，即随着α1的增大，臂架系统达到最佳稳定性时对应的θ1逐渐减小。

绘制θ1与α1的相互关系的等值线图，如图10所示。如图10中的黑色实线所示，θ1随α1的增大逐渐减小。如图10中的黑色虚线所示，α1随θ1的增大逐渐减小。

图8 L0与L1的相互关系的3D图Fig.8 3D figure of the correlation between L0and L1

图9 不同α1对应的θ1的影响曲线Fig.9 Influence curve ofθ1corresponding to differentα1

图10 θ1与α1的相互关系的等值线图Fig.10 The isogram of the correlation betweenθ1 andα1

绘制θ1与α1的相互关系的3D图，如图11所示。

3.3 θ2与α2的关系

保持L0=5 m，θ1=80°，L1=10.95 m，α1=90°不变，改变α2，得到不同α2条件下θ2对塔式副臂超起组合臂架系统整体稳定性的影响曲线，如图12所示。由图12可知，α2在［20°，140°］之间取值时，关于θ2的影响曲线在中间段变化较平缓，即偏心调整架撑杆变幅角度θ2对组合臂架系统的整体稳定性影响不大。

图11 θ1与α1的相互关系的3D图Fig.11 The 3D figure of the correlation between θ1and α1

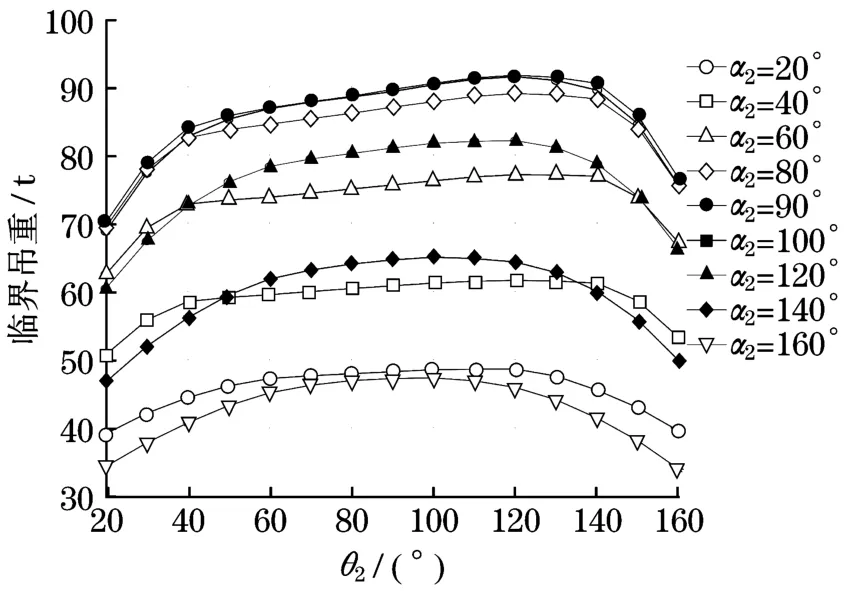
图12 不同α2对应的θ2的影响曲线Fig.12 Influence curve ofθ2corresponding to differentα2

绘制θ2与α2的相互关系的等值线图，如图13所示。绘制θ2与α2的相互关系的3D图，如图14所示。

图13 θ2与α2的相互关系的等值线图Fig.13 Isogram of the correlation between θ2and α2

图14 θ2与α2的相互关系的3D图Fig.14 3D figure of the correlation between θ2and α2

如图13中的黑色实线所示：α2小于120°时，偏心调整架撑杆张开角度θ2不随α2改变，θ2稳定在120°附近；α2超过120°后，θ2随α2的增大逐渐减小。如图13中的黑色虚线所示：α2基本不随θ2改变，α2稳定在90°附近。

4 结论

本文对塔式副臂超起组合臂架系统进行了特征值屈曲分析与几何非线性屈曲分析，结果表明：特征值屈曲分析得到的临界屈曲吊载明显高于几何非线性屈曲分析得到的结果，因此，应以几何非线性屈曲分析得到的临界屈曲吊载为准。通过研究偏心调整架与超起装置之间相互影响的规律，得到偏心调整架与超起装置参数之间的相互关系。分析参数之间的相互影响曲线可知：在选定工况为主臂长78.6 m、主臂仰角83°、塔式副臂21 m、副臂仰角48.4°时，超起撑杆长度L1的最佳取值为16 m，偏心调整架撑杆长度L0的最佳取值为6 m，超起撑杆张开角度α1的最佳取值为90°，偏心调整架撑杆的张开角度θ1为100°，超起撑杆的变幅角度α2的最佳取值为90°，即超起撑杆与伸缩主臂呈直角安装，偏心调整架撑杆的变幅角度θ2的最佳取值为120°，即偏心调整架撑杆相对伸缩主臂向上翘。