悬浮隧道整体结构行为机理试验研究4:激振方法构想与实践
2020-04-13曾繁旭周卓炜林巍邹威
曾繁旭 ,周卓炜 *,林巍 ,邹威
(1.中交悬浮隧道结构与设计方法研究攻关组,广东 珠海 519000;2.大连理工大学,辽宁 大连 116024;3.中交公路规划设计院有限公司,北京 100088)
1 概述
悬浮隧道作为一种新型的交通形式,在跨越深水域时,具有以下优势:单位造价不随跨度及水深的增加而急剧增长;受环境影响小,可全天候运行;对环境影响小;选址灵活等[1]。在1923年,挪威申请了世界上第1个关于悬浮隧道的专利[2]。近年来,海洋科学技术的发展极大的推动了悬浮隧道的研究,越来越多的学者对悬浮隧道进行广泛而深入的研究。目前关于悬浮隧道数值模型较多,且涉及到地震、撞击、缆索、接头、波浪作用、水流作用、流固耦合等各个领域,并且取得了丰硕的成果。数值模型常常引入较多假设,有效性与准确性有待进一步与模型试验进行相互验证。但至今尚未发现关于悬浮隧道(以下简称SFT)整体物理模型试验的相关文献。
为推动悬浮隧道的发展,2018年,中交悬浮隧道工程技术联合研究组牵头,在天津开展了悬浮隧道整体结构行为机理试验(以下简称“机理试验”)研究。了解结构的自振特性是深入了解其结构行为机理的前提。结合目前开展的悬浮隧道物理模型试验和参考桥梁工程及模型试验中测量自振特性的方法,本文对悬浮隧道可采用的自振特性测量方法进行了总结,介绍各个方法的基本原理、试验方法、注意事项及各个方法的优缺点。
2 自由振动衰减法
自由振动衰减可通过给模型施加初速度或初位移实现。由于结构的自振特性仅有自身刚度、质量和材料等因素有关[3],在模型试验中,通过给定管体初速度或初位移,使管体模型自由衰减运动,监测管体位移得到自由振动衰减曲线(图1)。对位移-时间数据进行傅里叶分析,频谱图谱峰频率即为管体的自振频率。结构体系阻尼比ξ可由式(1)计算:

式中:m,n为任意正整数;vn、vn+m为自由振动衰减曲线中出现的第n个、第n+m个位移幅值。应注意,冲击荷载作用位置应结合模型振型确定[4]。该模型平面运动的一阶振型在悬浮隧道跨中位置,二阶振型接近L/4处(L为隧道总长度)。

图1 自由衰减曲线Fig.1 Free decay curve
2.1 初速度法
通过锤击模型特征部位使其获得初速度,测量其自由振动衰减曲线进而得到悬浮隧道的自振特性(包括自振频率、阻尼比及振型)。在自振特性测量试验过程中,为了解析出管体的更多信息(如结构阻尼和附加水阻尼),提出定量敲击改进方案(图2)。在该方案中新增了支架和导轨,使得重锤冲击方向更加准确;当重锤作用到管体后,在弹簧的作用下可以与管体快速分离,避免重锤对自由衰减运动的影响;定位销可以固定重锤的初始位置,使每次冲击距离一定,保证模型试验的可重复性。在冲击锤头部安装冲击力测量装置,测量冲击过程中的冲击荷载-时间过程曲线,结合测得的结构响应,预期获得悬浮隧道结构阻尼和附加水阻尼信息。
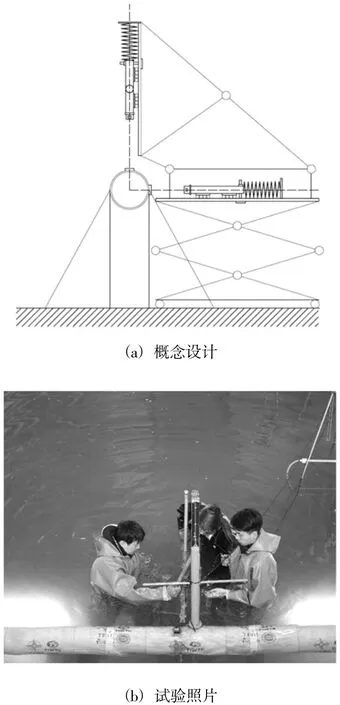
图2 定量敲击试验Fig.2 Strike with fixed and readableforce or energy
实践中发现敲击法应用到机理试验中存在一定问题。以管体L/4处加速度时间过程曲线及频谱分析(图3)为例,衰减曲线不光滑,估计是敲击过程中激发的波纹及破碎等因素带来较大的干扰;敲击法能量输入不足,管体运动衰减较快,导致频谱分析分辨率不足。如果增大撞击能量时,又有损伤模型风险。并且,当前从敲击法获得模型响应数据只见高阶模态,低阶模态较难被激发和观察到。
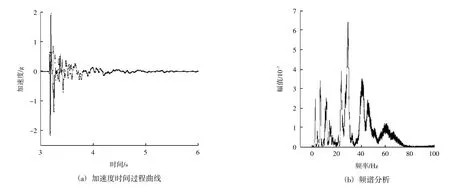
图3 管体L/4处垂向敲击实测结果Fig.3 Vertical strike at L/4 of tube
2.2 初位移法
初位移法通过缆绳连接模型让模型产生初始位移,再通过快速脱钩器或类似手段突然将缆力释放,结构在弹性恢复力作用下做有阻尼的自由衰减运动。缆绳自身几乎不可压缩,在缆绳上装有测力装置和测缆绳伸长量装置,后者近似等于结构集中力作用下产生的位移,通过力与位移也可检查结构体系刚度(图4)。该方法如果力足够大可以有效激发悬浮隧道基本模态,由于采用受控的静力加载,损坏模型风险相对较小。当需要激发悬浮隧道高阶模态时,需要在不同位置进行牵引,需要多套设备。该方法需要较多附属结构和基础处理。
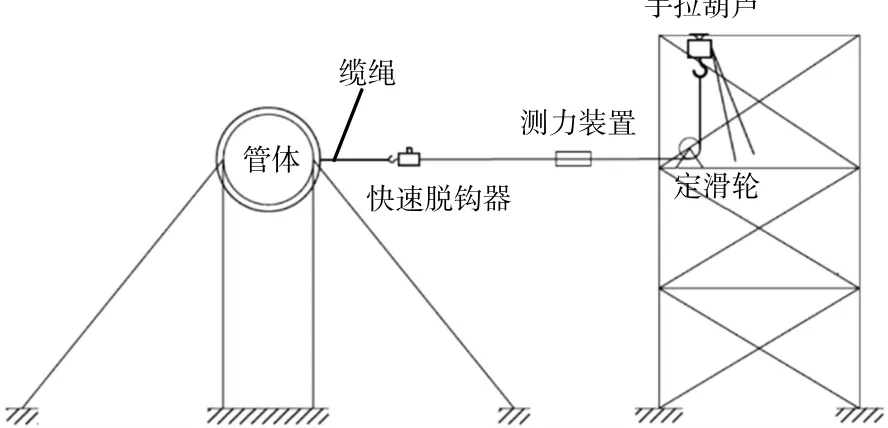
图4 初位移法水平牵引示意图Fig.4 Schematic diagram of horizontal traction with initial displacement method
3 共振法
由结构动力学可知,当外界输入频率与结构的固有频率相等时,会出现共振现象。在悬浮隧道模型试验中可采用经防水处理的激振器对结构施加简谐激振力,激振器类型包括惯性式、电动式、电磁式及电液式,断面构造见图5。通过不断改变激振器的振动频率,同时记录管体的振幅,绘制频率-振幅曲线(见图6),曲线中振幅的极值点相对应的频率即为悬浮隧道的各阶自振频率。黏滞阻尼比可以通过共振放大法和半功率法得到[5]。
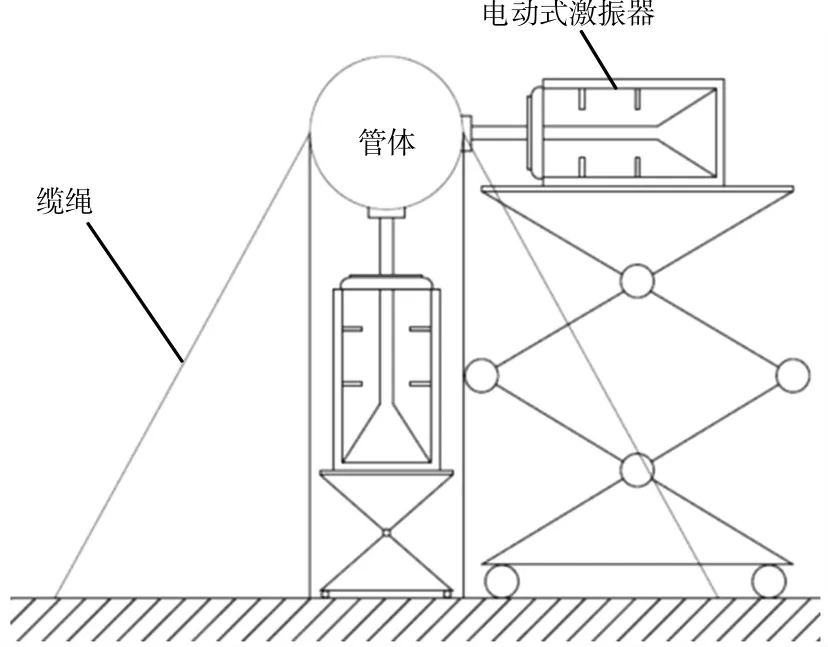
图5 共振法试验装置示意图Fig.5 Schematic diagram of resonance device
根据共振放大法可得:阻尼比ξ=ρ0/2ρmax。ρmax为不同频率简谐荷载作用下结构的最大位移,ρ0为相同幅值的静荷载作用下结构的静位移。根据半功率法,阻尼比 ξ=(β1+β2)/2,β1、β2是反应振幅等于最大振幅乘以1/时对应的频率比。与自由振动方法类似,简谐荷载的作用位置应结合待激发的管体振型确定。

图6 频率反应曲线Fig.6 Frequency response curve
在试验前调制激振器振动的频率及幅值,使不同频率时激振器输出的简谐力幅值相等。以惯性式激振器为例,激振器输出的简谐激振力可下式计算:

式中:F为惯性式激振器输出的简谐激振力,在不同频率时应取为定值;m为激振器质量;A为激振器运动幅值;ω为激振频率。
当激振频率变小时,可以调节输入信号,使激振器振动幅值增大,或者在激振器运动部件上添加质量块来实现不同激振频率下的简谐力幅值相等。同时,激振器输入频率应包含关心的管体前几阶自振频率。激振器的安装位置应结合待激发的结构振型确定。在初步确定结构自振频率后,可细化输入频率间隔,提高测试精度。
激励器能在所要求的频率范围内,提供波形良好、足够稳定的激振力。激振器可以输出足够的激振能量,激发出想要的结构振型,同时满足信噪比条件。不仅如此,使用激振器可以保证更为精确和可控的结果,因为激振器的输入不会受到力锤试验时人为操作误差的影响。该方法测试精度较高,对自振特性参数识别效果较好。但激振器自重会对悬浮隧道自振频率存在影响,并且激振器会影响悬浮隧道周围的流场。
4 脉动法
脉动法也称环境随机振动法,该方法测量环境中随机激励而引起的结构微幅振动响应,对该数据样本进行分析从而得到结构的自振特性。与共振法的原理类似,当结构处在由近似于白噪声信号的多种频率成分组成的随机振动中时,与结构物某阶自振频率相近的脉动频率就会由于“共振”效应使其波形显现出来。对结构运动信号进行分析得到振幅谱,通过振幅谱可确定结构自振频率,通过各峰处的半功率带可确定阻尼比。
脉动法对于柔性结构物的自振特性参数具有较好的识别效果,但对于频率高、刚度大的结构物识别效果不够理想;为了得到捕捉结构的微小振动,需要高灵敏、低噪声的传感器,并且需要大量数据样本,需要较长的观测时间;对自振频率的识别效果较好,但对阻尼比的直接识别效果较差[4]。
在进行悬浮隧道机理试验时,模型放置在试验水池中,白噪声信号可由造波机造出宽带谱波浪提供,不需要额外的激振设备。目前,白噪声不规则波被广泛的应用于船舶及海洋平台模型试验研究中[6]。理论上,白噪声谱密度是常量函数,其图形是一条延伸至+∞的水平直线(图7)。但实际上由于造波机造波能力的限制,对白噪声进行低频截止与高频截止,并且由于低频截止与高频截止附近波浪品质较差,常常设置一个过渡区,实际造波机输入谱形为梯形折线[7],白噪声谱与宽带谱如图7所示。为激发出结构前几阶振动频率,宽带谱有效频率范围应包含目标频率,宽带谱有效频率范围是由造波机性能决定的。以大连理工大学海岸及近海工程国家重点试验室多功能综合水池铰接推板造波机为例,该造波机生成波浪频率范围0.5~5 Hz。采用白噪声波浪作为激励存在一定限制。
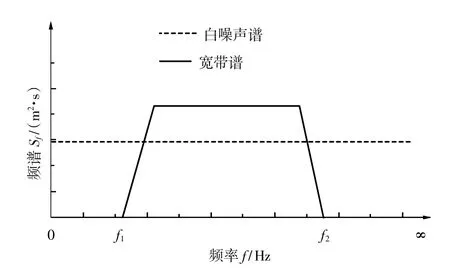
图7 白噪声谱与宽带谱Fig.7 Spectrum of white noise and broad brand
此外,也可以采用激振器输入宽带谱激振力实现脉动法。激振器以惯性式激振器GW-IV47/PA300E为例,此激振器工作频率范围DC-60 Hz,输出最大简谐力250 N。可以看出此方法工作频率范围更大,可以有效覆盖待测的悬浮隧道频率范围,应用范围更广。但需要专门的激振设备,并且激振设备需要进行防水处理,激振信号需要特别调制。
5 激振方法比较
各种激振方法的优缺点统计见表1,从激振效果、适用性以及经济合理性角度综合考虑,推荐初位移法(拉线法)作为悬浮隧道结构行为机理试验研究采用的激振方式。
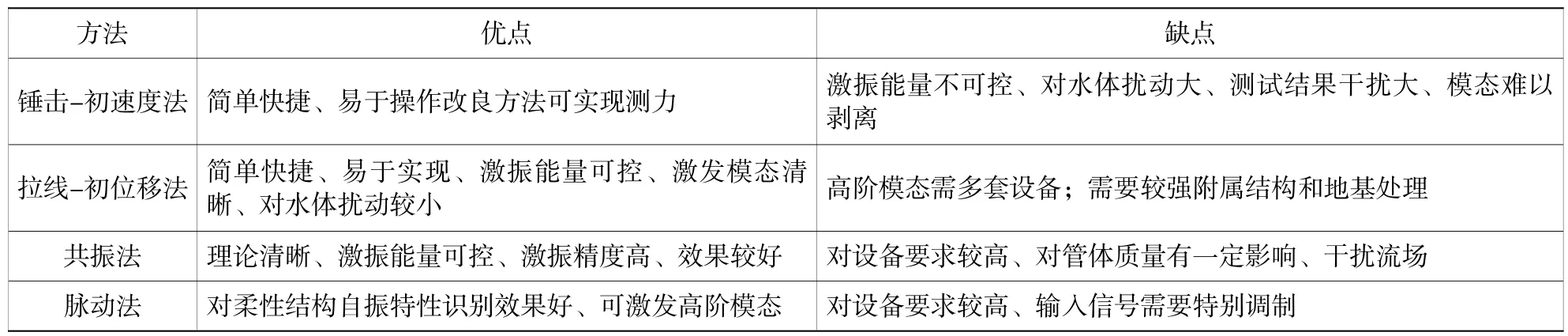
表1 悬浮隧道模型激振方法比较Table1 Comparison of excitation methods for SFT model
6 结语
机理试验在试试验阶段采用捶击法,后改良为定量锤击法,然而仍然无法有效剥离工程设计人员所关心的前几阶结构响应。作者提出缆绳-快速脱开、共振法和脉动法构想。并与已有方法进行了优缺点比较。后续试验工作可结合现场条件与试验安排酌情考虑。
