偏序集上的way-up关系

2020-04-13徐款款

苏州科技大学学报(自然科学版) 2020年1期

徐款款，卢涛

（淮北师范大学数学科学学院，安徽淮北235000）

文献[1]详细地给出了way-below 和辅关系的定义及其相关性质。受此启发，笔者在已有way-up 关系概念的基础之上，借助way-up 关系和新的辅关系的定义讨论了way-up 关系在偏序集、并连续半格及余dcpo不同背景下的性质；然后，在余dcpo 上给出了逼近辅关系的定义并研究其相关性质；最后，从范畴论[2-3]的角度考虑，给出了局部余定向完备范畴的概念，并将偏序集上的way-up 关系转移到局部余定向完备范畴上，讨论了局部余定向完备范畴上way-up 关系的相关性质。

1 预备知识

定义 1[1]设（L，≤）是偏序集，S⊆L。若 S≠Ø，并且 S 中的任意二个元在 S 中都有下界，即∀a，b∈S，有c∈S，使得 c≤a，c≤b，则称 S 是余定向的。

定义2[1]设（L，≤）是偏序集。若对于L 的任意定向子集S，∨S∈L 都存在，则称偏序集（L，≤）有定向并或称（L，≤）是定向完备的。定向完备的偏序集也称为dcpo。

定义3[4]设L 是偏序集，x，y∈L，对任意的余定向集M⊆L，若inf M 存在，且y≥inf M，存在m∈M，使得x≥M，则称 x way-up y，记作 x≫y。当 x≫x 时，称 x 是 L 的余紧元。

注1在偏序集L 中，x≫y 能推出x≥y；反之不成立，如图1、图2 所示。

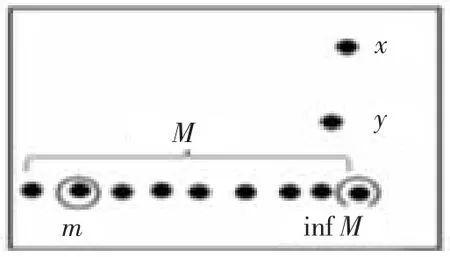
图1 x≫y

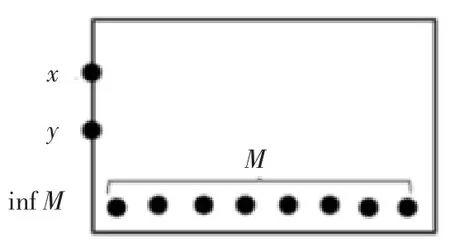
图2 x≥y 但 x≫y 不成立

注2在完备半格L 中（特殊地，在完备格中），way-up 关系可以与以下性质等价：

x≫y⇔对任意子集X⊆L，当y≥inf X 时，蕴含着存在有限子集A⊆X，使得x≥inf A。事实上：令余定向集X-={inf A:有限集 A⊆L}，则 inf X-=inf X。因此，若 x≫y，由定义可知：若 y≥inf X，存在有限集 A⊆L，使得x≥inf A。反之为显然。

定义4[1]设L 是偏序集，对于a∈L 与S⊆L，规定

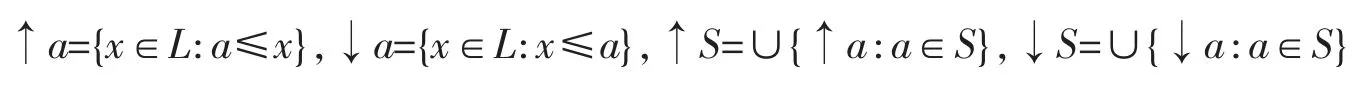
当 S=↓S 时，称 S 是下集；当 S=↑S 时，称 S 是上集。

定义5[5]设L 是半格。若L 是定向完备的，即dcpo，并且对任意的x∈L 和定向集D⊆L 满足

则称L 是交连续的。并半格L 是并连续的当且仅当Lop是交连续的。

定义6设L 是偏序集。若L 是一个半格且是余定向完备的，则称L 是余定向完备半格。

定理1在余定向完备半格L 中，以下结论等价：

（1）L 是并连续的；

（2）对任意的余定向集 D，当 x≥inf D，有 x≥inf（x∨D）（因此，x＝inf（x∨D））。

定义7[1]设（L，≤）是偏序集。若对于L 的任意余定向子集D，∧D∈L 都存在，则称偏序集（L，≤）是余定向完备的。以下简记余定向完备偏序集为余dcpo。

定义 8[6]设 L 是一个小范畴，D:J→L 是一个 J 型图。称 D 是一个滤子图表，如果对任意 j，j′∈obJ 的都存在 i∈obJ，使得 D（i）→D（j），D（i）→D（j′）。

以下研究way-up 关系的相关性质。

2 way-up关系的相关性质

定理2设L 是偏序集，元素p∈L 是余紧元当且仅当p≫p（即对任意的余定向集D⊆L，且inf D 存在，若 p≥inf D，则存在 d∈D，使得 p≥d）。

记K（L）={x∈L:x≫x}是L 的所有余紧元构成的集合。

注 3设 L 是完备半格，（特殊地 L 是完备格），p∈K（L）当且仅当对任意的 D⊆L，p≥inf D 蕴含着存在有限集 F⊆D，使得 p≥inf F。事实上：设余定向集合 X-={inf F:F⊆D，F 有限集}且 inf X-=inf D。因此，若 p≫p，由定理2 可知：若p≥inf D，则存在有限集F⊆D，使得p≥inf F。反之为显然。

例 1若 L 是单位区间，则 K（L）={1}。

命题 1设 L 是偏序集，对任意的 x，y，z，w∈L，以下结论成立：

（1）x≫y⇒x≥y；

（2）w≥x≫y≥z⇒w≫z；

（3）x≫z 且 y≫z⇒若 x∧y 存在，则 x∧y≫z；

（4）1≫x，即 L 有最大元 1。

证明（1）由 x≫y 知：任取余定向集 D⊆L，若 inf D 存在，且 y≥inf D，则存在 d∈D，使得 x≥d，故可取y=d，则有 x≥y。

（2）任取余定向集 D⊆L 且 inf D 存在。若 z≥inf D，由 y≥z 知：y≥inf D。因为 x≫y，则存在 d∈D，使得x≥d。又因为 w≥x ，从而 w≥d。故 w≫z。

（3）任取余定向集 D⊆L 且 inf D 存在。若 z≥inf D，由 x≫z 知：存在 d1∈D，使得 x≥d1。再由 y≫z 知：存在d2∈D，使得 y≥d2。因为 D 为余定向集，所以存在 d∈D，使得 d1∧d2≥d，所以 x∧y≥d1∧d2≥d。故 x∧y≫z。

（4）任取余定向集 D⊆L，设 x≥inf D。而∀d∈D，有 1≥d，故 1≫x。

显然由（1）（2）知，≫是满足传递性和反对称性，记

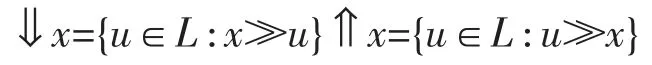
注4设L 是完备格，x∈L，集合⇑x 是包含于↑x 的滤子。若 x≥y，则⇑x⊆⇑y。

例 2设 L 是完备链，x＞y 蕴含着 x≫y。相反，若 x≫y，则 x＞y 或 x=y 或 x=1。事实上：inf（↑x{1}）＞x，所以x 是跳跃的右端点，因此，若 L 是平凡单位区间[0，1]，则 x≫y⇔x＞y 或 x=y=1。

设 L 是偏序集，x∈L，记 J（x）={F∈Filt（L）:x≥inf F}。

命题2设L 是偏序集，以下结论等价：

（1）x≫y；

（2）对任意满足 y≥inf D 的滤子 D，有 x∈D；

（3）x∈∩J（x）。

证明（1）⇒（2）由定义知：显然。

（2）⇒（1）设余定向集 F⊆L，且 y≥inf F，则 D=↑F 是滤子，从而 y≥inf F=inf D。由（2）知：x∈D，即存在d∈D，使得 x≥d，故 x≫y。

（3）是（2）的另一种形式。

命题3若L 是并连续半格，则以上三个命题和以下结论等价：

对任意满足y=inf D 的滤子D，有x∈D。

证明在并连续半格中，y≥inf D⇔y=inf（y∨D）。

命题4设存在余定向集D⊆⇑x，且x=inf D，则⇑x 是余定向的，且x=inf ⇑x。

证明设 y≫x，z≫x，则存在 d1，d2∈D，使得 y≥d1，z≥d2。因为 D 是余定向的，则存在 d∈D，使得 d1≥d，d2≥d，从而有 y≥d，z≥d 且 d≫x，因此，⇑x 是余定向的，且 x=inf ⇑x。

定义9设L 是偏序集，≻是L 上的二元关系。若对任意的x，y，z，w∈L，满足以下条件：

（1）x≻y⇒x≥y；

（2）w≥x≻y≥z⇒w≻z；

（3）若最大元 1 存在，则 1≻x。则称≻是L 上的辅关系。

设L 是偏序集。若L 有最大元1，记UppL 表示在L 中所有包含1 的上集构成的集合。

由命题 1 可知：⇑x=∪{D∈Filt（L） :x≥inf D}。设 L 是余 dcpo，对任意的滤子 D∈Filt（L）映射 mD:L→UppL，其中

则 mD（x）是上集且↑x⊆mD（x），而且是保序的，也就是说 mD∈M。其中

定义10设L 是余dcpo。 L 上的辅关系≻称为逼近的，如果集合{u∈L:u≻x}=s≻（x）是余定向的（因此，是一个滤子），且对任意的 x∈L，有 x=inf{u∈L:u≻x}=inf s≻（x）。

显然，关系≥是平凡逼近的。

引理1在并连续半格L 中，对于任意的D∈FiltL，所有包含于映射mD的关系是逼近的。

证明设 x∈L，D∈FiltL，显然 mD（x）是有下界的余定向集，所以 inf mD（x）存在。下证 x=inf mD（x）。若x≥inf D，则 inf mD（x）=inf（x∨D）=x∨inf D=x。若 xinf D，则 inf mD（x）=inf↑x=x。

命题5设L 是余dcpo，则L 上的way-up 关系≫包含于所有逼近的辅关系。

证明设 y≫x 且≻是逼近辅关系，则集合 s≻（x）={u∈L:u≻x}是余定向的，且 x=inf{u∈L:u≻x}，从而存在一个 u∈L，使 y≥u≻x，因此，y≻x。故 L 上的 way-up 关系≫包含于所有逼近的辅关系。

命题6设L 是余dcpo，考虑以下条件：

（1）关系≫是L 上的最小的逼近辅关系；

（2）L 中存在一个最小的逼近辅关系。则（1）⇒（2）。

定义11设L 是偏序集，≻是L 上的辅关系。若∀x，z∈L

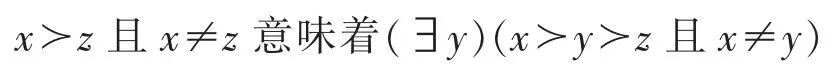
则称辅关系≻满足强插入性质。

引理2设L 是余dcpo，则L 上的任意逼近辅关系≻满足以下结论：对∀x，z∈L

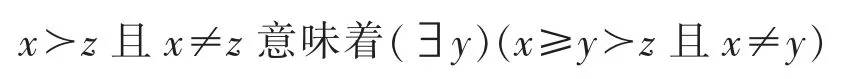
证明设 x≻z 且 x≠z。因辅关系≻是逼近的，从而 s≻（z）={u∈L:u≻z}是余定向的且 z=inf{u∈L:u≻z}，则存在 u≻z 且 ux。又因为{u∈L:u≻z}=s≻（z）是余定向的，则存在{x，u}的下界 y，使得 y≻z，从而 x≥y≻z。由于 ux，则 x≠y。

定理3设L 是余dcpo，则L 上的任意逼近辅关系≻，有以下结论成立：对∀x，z∈L

（1）设集合 D⊆L 是余定向的。若 x≫z，x≠z 且 z≥inf D，则存在元素 y∈D，使 x≻y 且 x≠y。

（2）若 x≫z 且 x≠z，则存在一个 y，使得 x≻y≻z 且 x≠y。

证明（1）设集合 D⊆L 是余定向的且 z≥inf D。设 F=∩{s≻（d）:d∈D}。因为 F 是滤子，所以 inf F=inf{inf s≻（d）:d∈D}=inf D≤z，则关系≻是逼近的。由 x≫z 可知：x∈F。因此，存在元素d∈D，使得 x≻d。因为xz 且 z≥inf D，则存在元素 c∈D 且 cx。令 y 是{c，d}在 D 中的下界，则 y 满足命题条件：y∈D，使 x≻y 且x≠y。

（2）取余定向集 D={y∈L:y≻z}=s≻（z）。因为辅关系≻是逼近的且 z=inf D。若 x≫z 且 x≠z，由（1）可知：可以找到一个元素 y∈D，使 x≻y 且 x≠y，从而有 x≻y≻z 且 x≠y。

接下来从范畴论的角度将偏序集上的way-up 关系推广到任意小范畴上，引入局部余定向完备范畴的定义，并把way-up 关系转移到局部余定向完备范畴上。

3 局部余定向完备范畴及其上的way-up关系

该节所涉及到的范畴都是小范畴。记一个范畴L 中的态射为→。对任意的x∈obL，记↑x={y∈obL:x→y}。

定义12设L 是一个小范畴，若L 中的每一个滤子图表D 的下确界iolim D 都存在，则称L 是一个余定向完备范畴。

定义13设L 是小范畴，若对任意的a∈obL，↑a={x∈obL:a→x}为余定向完备范畴，则称L 是局部余定向完备范畴。用iolimaD 表示滤子图表D:J→↑a 在↑a 中的下确界。

注5余定向完备范畴是局部余定向完备范畴。

定义14设L 是局部余定向完备范畴，x，y∈ob。若对L 中任意一个有下界的滤子图表D:J→L 与它的一个下界 b，如果存在态射 iolimbD→y，则总有 j∈obJ，使得 D（j）→x 成立，则称 x way-up y，记作 x⇐y。

命题 7设 L 是局部余定向完备范畴，则对任意的 u，x，y，z∈obL，有

（1）若 x⇐y，则 y→x；

（2）若 u→x⇐y→z，则 z⇐u；

（3）若 L 有终对象 1，则 1⇐x。

证明（1）取 D（obJ）={y}。若 x⇐y，由定义 14 可知：y→x。

（2）设u→x⇐y→z。对L 中任意一个有下界的滤子图表D:J→L 与它的一个下界b，如果存在态射iolimbD→u，则有 iolimbD→y。又因为 x⇐y，则存在 j∈obJ，使得 D（j）→x 成立，从而 D（j）→z。因此，z⇐u。

（3）对L 中任意一个有下界的滤子图表D:J→L 与它的一个下界b，如果存在态射iolimbD→x，因为1 是终对象，则总有 j∈obJ 使得 D（j）→1。故 1⇐x。

定义15设L 是范畴且具有终对象。称obL 上的二元关系为辅关系，如果对于任意的u，x，y，z∈obL，满足以下条件：

定义16设L 是局部余定向完备范畴。称定义在obL 上的辅关系为逼近的，如果s(x)={u∈obL:ux}是余定向的且对任意的x∈obL，有

记obL 上的所有逼近的辅关系构成的集合为App（obL）。

命题8在局部余定向完备范畴中，way-up 关系包含于所有逼近的辅关系。

证明设 y⇐x,∈App（obL），则集合{u∈obL:ux}是余定向的，且对∀x∈obL，有于是存在 u∈obL，使得 ux→y，由定义 15（2）可得：yx。故 way-up 关系包含于所有逼近的辅关系。

引理3设L 是局部余定向完备范畴，则obL 上的任何逼近的辅关系满足条件：对任意的x，z∈obL，若 xz 且 x≠z，则存在 y，使得 zy→x 且 x≠y。

证明设 xz 且 x≠z。因为是逼近的辅关系，则 s（z）={u∈obL:uz}是余定向的且uz}。于是存在 u∈obL，使得 uz 但 x→/ u。又 s（z）是余定向的，所有存在 x 与 u 的一个下界 y，即 y→x，y→u，使得 zy。因此，zy→x 且 x≠y（否则与 x→/ u 相矛盾）。

定理4设L 是局部余定向完备范畴，则obL 上的任何逼近的辅关系满足下列条件：对∀x，z∈obL。

（1）设 L 中任意一个有下界的滤子图表 D:J→L 与它的一个下界 b。若 x⇐z，x→/ z 且存在态射则存在 y∈D（obJ），使得 xy 且 x≠y；

证明（1）设D:J→L 是L 中任意一个有下界的滤子图表，它的一个下界为b，且存在态射由辅关系是逼近的可知：s（d）是余定向的且若 x⇐z，则存在 i∈B，使得 i→x，即存在 d∈D（obJ），使得 di→x，从而 xd。由知：存在 e∈D（obJ）使得 x→/ e。令 y 是 d 与 e 在 D 中的下界，从而 y∈D（obJ）且 y→d，y→e。故 xy 且 x≠y。

（2）取 D=s（z）={y∈obL:yz}。因为辅关系是逼近的，则 D 是滤子图表且如果 x⇐z 且由（1）知：可以找到 y∈D（obJ），使得 xy 且 x≠y，从而有 xyz 且 x≠y。