一种基于PSO-RBF网络算法的热舒适性指标预测新方法
2020-04-13朱其新周敬松朱永红
陆 烨, 朱其新, 周敬松, 朱永红
(1.苏州科技大学 环境科学与工程学院,江苏 苏州 215009;2.苏州科技大学 机械工程学院,江苏 苏州 215009;3.景德镇陶瓷大学 机电工程学院,江西 景德镇 333001)
Fanger 教授于1970 年提出热舒适指标预测平均投票值(predicted mean vote,PMV)以来,PMV 已成为目前国际上应用最为广泛的室内热舒适评价指标。 该指标是Fanger 教授在建立两节点人体热平衡模型的基础上,通过收集1 396 名受试者对环境冷热感觉的反应后,利用回归公式使人体热舒适指标量化[1]。 由于PMV指标综合考虑了室内空气湿度、温度、气流、辐射、人体情况等多种因素,从而使得PMV 指标在室内环境控制中有着广泛的应用。
Kaya 等人提出同时控制房间的温度、相对湿度和风速三个参数的设定值,使室内环境状态达到并保持在ASHRAE 所推荐的舒适性区域,从而使系统能耗达到最低[2]。随后MacArthu 首先提出用PMV 指标值作为控制对象,还提出了两种基于PMV 指标的控制策略,即直接PMV 控制和基于房间湿度的温度再设控制,结果表明,与传统的温度控制相比,基于PMV 指标的控制方式节能效果达5%~14%[3]。由于PMV 指标值影响因素较多,Scheatzle 教授提出将PMV 指标作为一种标准来指导控制[4],控制策略采用“专家系统”,研究结果表明,此种方法的节能效果可观。 为了实现PMV 指标的具体控制,Tse 针对影响舒适度的各种环境因素特点,分别对其进行独立控制[5],控制器采用PID 控制,结果表明,PMV 控制在提高房间舒适性上有非常好的效果,但节能与否取决于气候类型。 Liang J 与DU R 提出智能建筑中央空调系统的舒适度控制方法[6],通过在线学习室内人员的舒适偏好,相应地调节空调控制参数,最终达到舒适与节能。为了研究基于PMV 舒适性指标控制的适用性,王海英、胡松涛等分析了PMV 指标预测偏差产生的原因,随后在对PMV 预测误差的分析中指出,由于人体的衣着热阻和新陈代谢的不准确测量,可使模型预测准确率减少20%~25%,而个体差异、建筑类型和人的适应性对PMV 预测的准确性亦有非常大的影响,研究结果认为,PMV 热舒适性指标模型在预测空调建筑时较为准确,但不适用于自然通风建筑[7]。 李慧等提出动态热舒适控制系统概念,采用模糊学习算法在线修改个人舒适区,通过计算实验,进行舒适区和节能区的动态控制,结果指出,相对于静态热舒适系统,动态热舒适系统更有利于健康和节能[8]。 在同一时间,段培永提出采用超闭球的神经网络进行室内湿度的预测[9],随后又提出基于粒子群优化的室内动态热舒适度控制方法[10],通过改进的多目标粒子群优化算法得出动态热舒适度控制系统输入参数的寻优方法。 加州大学工程学院的Siyu Wu 和Jianqiao Sun 提出一种关于热舒适性指标的两阶段回归模型预测算法[11],通过回归分析,采用灰箱数字模型方法预测建筑结构参数和环境控制变量对PMV 指标的影响,结果表明,该方法在确定系数大于0.96 时,均方根误差小于0.04。 为了更加精准地对PMV 指标的控制,Sajid Hussain,Hossam A.Gabbar 和Daniel Bondarenko 等人采用遗传算法(GA),在 Matlab 中优化模糊逻辑控制器(FLC)的关系函数(MFs)和模糊规则矩阵(FRMs)[12],根据 PMV 指标的范围,在EnergyPlus 中计算温度设定值,结果表明,此种基于PMV 指标的控制方法在制冷和采暖工况下节能率分别为16.1%和18.1%。
通过以往对基于PMV 指标的空调控制的研究, 可以看出,PMV 作为一个衡量室内舒适与否的指标,其计算公式不仅非常复杂,而且还是非线性的,其数学表达式不适合应用于室内环境智能控制系统中[13]。 在以往的研究中,虽然已有较多的方法来预测PMV 指标并对其进行相应的控制,但对于PMV 指标的预测模型大多较为复杂,且预测结果的误差还不是很理想,笔者采用粒子群算法对RBF 神经网络进行优化,建立了预测PMV 指标的神经网络模型,该模型不仅结构简单,而且减小了预测误差,为实现基于PMV 指标节能舒适型空调控制创造有利条件。
1 PMV指标简介
PMV 是一种广泛采用的用以直观反应冷暖感觉程度的环境指标。它是Fanger 在热舒适方程的基础上建立起来的,通过主观感觉实验采用ASHRAE 热感觉分级法确定的大多数人对热环境的平均投票值。 PMV 可以适用于各种环境,它综合了室温、空气湿度、风速、平均辐射温度、服装热阻和人体活动量六个因素的影响。其表达式[1]为
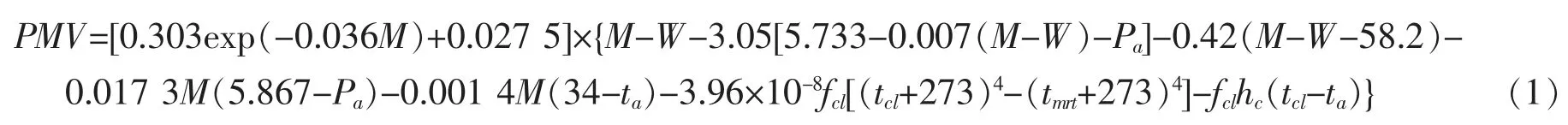
其中:M 为人体的新陈代谢率;W 为人体对外所做的机械功率;ta为人体周围的空气温度;tmrt为房间的平均辐射温度;Pa为环境空气中水蒸气分压力,由湿度传感器测得的相对湿度RH 和人体周围的空气温度ta求得

tcl为衣服外表面温度
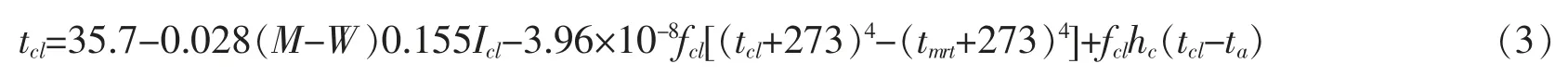
fcl为服装面积系数,用来表示人体着装后的实际表面积和人体裸身表面积之比

Icl为服装热阻值,hc为对流交换系数

va为相对空气流速。
以PMV 作为热舒适感的主观评价指标,分为七个等级,其取值范围在-3 至3 之间,分别表征了人体对于热程度的感知水平,具体的分度表见表1。

表1 人体对热感知的分度表
2 粒子群算法的基本原理
粒子群算法,也称粒子群优化算法(particle swarm optimization,PSO),是一种新型的仿生算法,由Kennedy和Eberhart 于1995 年提出[14-15]。PSO 因其需要调节的参数少,具有简单且易于实现的优点,因此,能够有效地优化各种函数、神经网络等。
在PSO 算法中,每个优化问题的解都是搜索空间中一个粒子[16]。所有的粒子都有一个被优化的函数决定的适应度值,每个粒子还有一个速度(v)决定他们飞行的方向和距离。PSO 初始化为一群随机粒子,然后粒子根据当前的最优粒子在解空间中搜索最优解。 在每一次迭代中,粒子都是通过跟踪两个“极值”来更新自己,一个是粒子自身找到的最优解,称为个体极值(pbest);另一个极值是整个群体找到的最优解,称为全局极值(gbest)。 如果粒子的群体规模为 M,目标搜索空间为 D 维,则第 i(i=1,2,…,M)个粒子的位置可表示为 Xi,它所经过的“最好”位置记为pi,速度用Vi表示,群体中“最好”粒子的位置记为pg,那么粒子i 将根据下面的公式来更新自己的速度和位置

其中,k 为迭代次数,d=1,2,…,D,c1、c2为大于零的学习因子或称作加速系数,r1、r2是[0,1]上的随机数。
3 PSO-RBF网络算法
3.1 RBF神经网络结构分析
RBF 神经网络是具有单隐层的3 层前馈网络。 它模拟了人脑中局部调整、相互覆盖接收域(或称感受域,Receptive Field)的神经网络结构,已证明RBF 网络能以任意精度逼近任意连续函数[17]。
RBF 网络由输入到输出的映射是非线性的, 而隐层到输出的映射是线性的,网络中的作用函数是高斯基函数,其中在输入空间中有限范围内为非零值,因而RBF 网络是局部逼近的神经网络。采用RBF网络可以大大加快学习速度并避免出现局部极小问题,适合于实时控制的要求。
多输入单输出的RBF 网络结构如图1 所示。
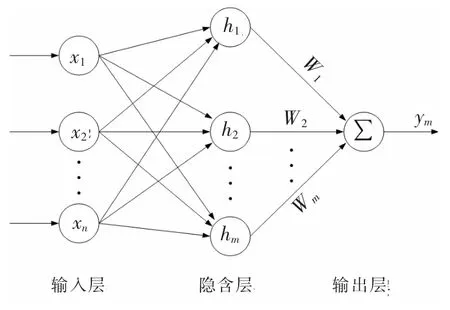
图1 RBF 神经网络结构图
在RBF 神经网络中,设x=[x1x2…xn]T为网络输入,hi为隐含层第i 个神经元输出,即

式中,i=1,2,…,m,ci=[ci1,…,cin]为第 i 个隐层神经元的中心点向量值。
高斯基函数的宽度向量为

式中,bi>0 为隐含层神经元i 的高斯基函数的宽度。
网络的权值为

RBF 网络的输出为

由于RBF 网络只调节权值,因此,RBF 网络算法简单、运行时间较快[18]。 但由于RBF 网络中,输入空间到输出空间是非线性的,而隐含空间到输出空间是线性的,因而其非线性能力较差。所以标准的RBF 网络对于PMV 的计算,效果并不理想,而PSO 算法[19]能很好地优化RBF 网络权值,可以较好地弥补其非线性能力较差这一缺点。
3.2 PSO算法优化RBF网络
3.2.1 PSO 算法确定基函数中心值和宽度
在PSO 算法中,一个粒子对应于一个可行解,首先对粒子编码,编码中包括基函数中心值和宽度、粒子速度及适应度。 假设为m 个中心,每个中心迭代k 次,那么粒子位置迭代次数为m(k+1),粒子速度迭代次数也为m(k+1),σi表示第i 个基函数的宽度,fi表示第i 个个体的适应度。 则粒子的编码结构如下

3.2.2 PSO 算法确定隐含层到输出层连接权值
基函数的中心值和宽度确定后,就可以得到隐含层输出hi,从而只要再确定隐含层到输出层的连接权值即可得到最终输出。 这里用欧式范数作为适应度函数:G=||Yi-hi||。
3.2.3 用PSO 算法确定RBF 网络权值的基本步骤
步骤1 采集数据样本;
步骤2 初始化粒子群的种群;
步骤3 对每个粒子,比较它的适应度fi与它所经历的最好位置的适应度,如果更好,更新pbestid;
步骤4 对每个粒子,比较它的适应度fi与群体所经历的最好位置的适应度,如果更好,更新gbestid;
步骤5 调整粒子的速度和位置;
步骤6 重复步骤3 到5,直到达到计算要求为止;
步骤7 将群体所经历最好位置解码后得到基函数的中心位置及宽度;
步骤8 计算隐层单元输出hi及输出层输出Yi;
步骤9 重新初始化粒子群的种群,调整权值wi,适应度函数为G=||Yi-hi||;
步骤10 对每个粒子,比较它的适应度G 与它所经历的最好位置的适应度,如果更好,更新pbestid;
步骤11 对每个粒子,比较它的适应度G 与群体所经历的最好位置的适应度,如果更好,更新gbestid;
步骤12 调整粒子的速度和位置;
步骤13 重复步骤10 到12,直到达到计算要求为止;
步骤14 解码得到RBF 神经网络需要确定的所有参数,对网络进行学习;
步骤15 停止运算。
4 PMV指标预测模型的训练与评价
根据以上叙述,这里选取6 个网络输入点,即影响人体热舒适的主要六个影响因子:人体的新陈代谢量、服装热阻、人体对外做功、空气温度、空气相对湿度以及空气流速。 输出节点数为1 个,即PMV 的值;由于RBF 网络主要是对隐含层数量的优化,而PSO 算法是对其中间的权值进行优化,所以,为了更好的体现PSO的优化性能,文中选取RBF 网络的隐含层节点数为10。 PSO 的仿真相关参数有:种群规模为100,加速常数c1、c2均为2,最大最小权重分别取0.9 和0.3,种群适应度方差阈值为10。
根据《民用建筑供暖通风与空气调节设计规范》GB50736-2012[20],对六个影响因子进行条件设定:人体新陈代谢量,静坐时为58.2 W/m2,站立或轻作业时为69.775 8 W/m2;服装热阻,0.3~0.7 W/m2;人体对外做功,静坐时一般为0;空气温度,22~28 ℃;空气流速为0.2~0.3 m/s;空气相对湿度为40%~80%。考虑到冬夏季节的空调参数不同,以及对PMV 值更加准确的预测,故而均选取夏季参数。
通过Matlab 对上述六个因子的数值进行随机取样并随机组合,为验证可行性,通过计算得到1 000 组样本数据,其中随机抽取700 组作为学习样本,剩余300 组作为评价样本。为了更好地反映预测模型的性能,在输入前先对样本数据的输入和输出参数做归一化处理。
文中用标准的RBF 网络和PSO 优化后的RBF 网络分别对所选的样本进行了训练,结果如下:
(1)图2 为由标准RBF 网络下对学习样本进行训练的结果,图3 为由PSO 算法优化后的RBF 网络下对学习样本进行训练的结果。 比较优化前后的训练情况可以看出,原始的RBF 网络训练后的误差精度为0.054 884, 而经过PSO 算法优化后的RBF 网络训练后的误差精度为0.011 23, 误差精度提高了79.5%,效果明显。
(2)为了验证训练结果是否正确,对评价样本进行预测,预测结果与先前通过计算法得到的PMV 值进行了对比,在标准的RBF 网络预测下,其误差均方根为0.052 105,在PSO 算法优化后的RBF 网络预测下,其误差均方根为0.009 887 7,同时绘制出图4 所示的预测误差对比图。
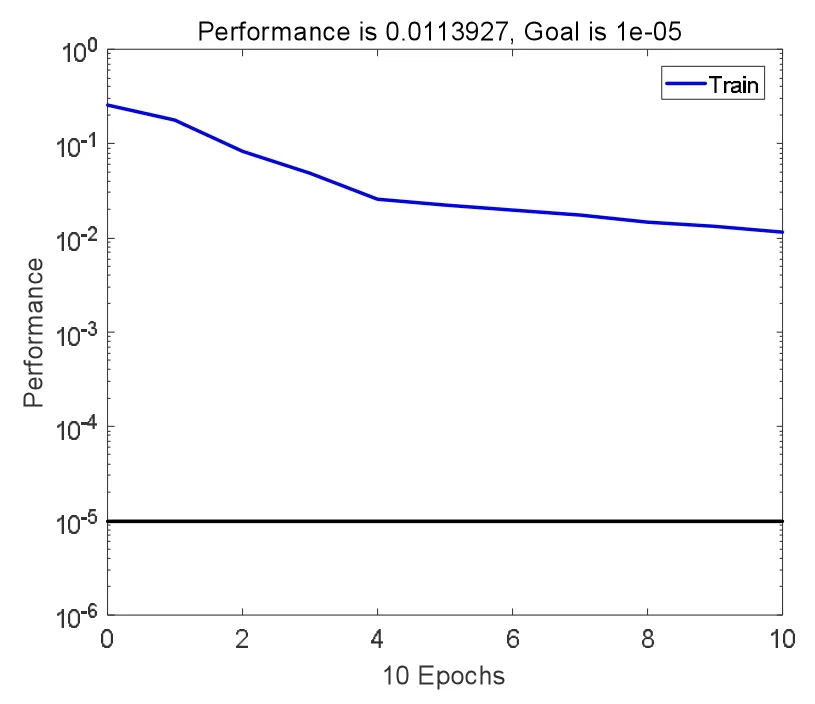
图2 RBF 网络训练结果

图3 PSO-RBF 网络训练结果
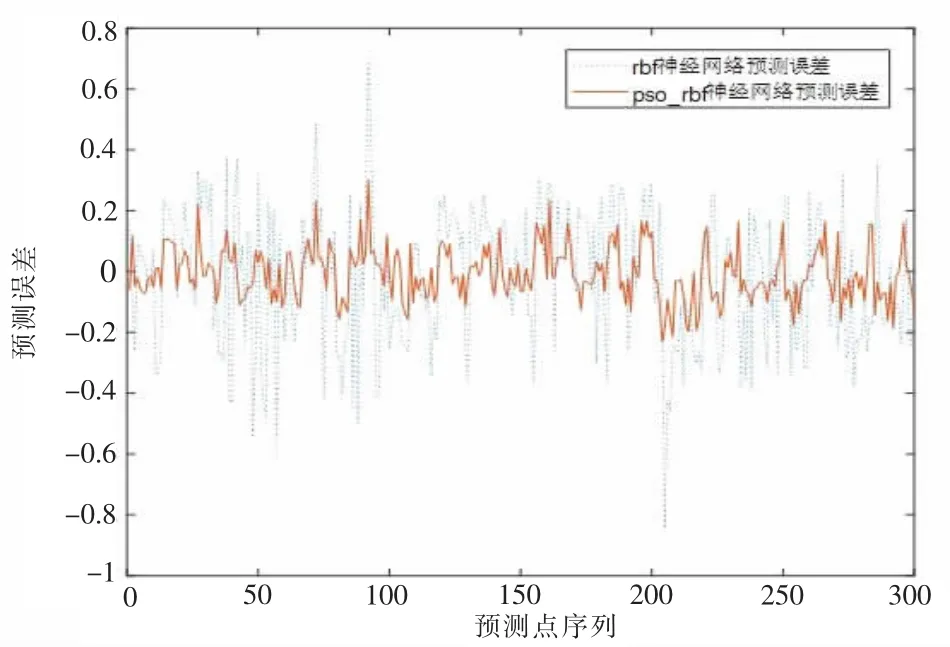
图4 误差对比图
由图4 可见通过PSO 算法对RBF 网络进行优化后,其误差显著减小,更加适合对PMV 指标的预测。
5 结语
通过采用PSO 算法对RBF 网络进行优化,有效地提高了传统RBF 神经网络的误差精度,通过优化后的网络误差精度提高了79.5%,误差均方根减小了81%,效果显著。
目前的空调控制中大多数是以室内温度作为控制参数,难以创造出真正舒适的室内环境,而且还会导致空调系统能耗的增加。文中提出了将PMV 指标引入空调控制,并解决了PMV 指标相关的非线性因素在空调实时控制中的不能直接测量的问题,为实现基于PMV 指标的空调系统实时控制创造了良好的条件。
