基于算理、算法、算律三类课堂提高学生的运算能力

蔡芬芬

【摘 要】算理型课堂是从运算的意义出发，理解运算道理的课堂;算法型课堂是在算理的基础上构建运算法则的课堂;算律型课堂是在算法的基础上概括运算规律的课堂。算理、算法和算律对数学运算能力有重要的影响，只有在课堂上将算理、算法和算律紧密结合，才能更好地提升学生的运算能力。

【关键词】算理型课堂;算法型课堂;算律型课堂;运算能力

运算能力不是简单地掌握加、减、乘、除的计算，而是一种与观察能力、记忆能力、理解能力、推理能力、表达能力及想象能力等有关的由低级到高级的综合能力。曹培英进一步提出数学运算能力包括“基本口算、掌握算法、理解算理、运算策略”这四个结构，说明“算理、算法和算律”对数学运算能力有重要的影响[1]。现以北师大版小学数学教材为例，谈一谈如何基于算理、算法、算律的课堂有效提升学生运算能力。

1   算理型课堂

算理型课堂是从运算的意义出发，理解运算道理的课堂。小学数学的计算教学常以口算或简单计算为起点，内容比较简单，学生比较容易掌握。所以教师有时会讲得比较简略，忽略通过实际意义理解算理的过程。计算教学中，教师应放慢教学节奏，从“说意义”过渡到“讲算理”。

1.1  低年级的算理型课堂

在小学低年级的算理型课堂中，可以让学生通过操作实物来理解意义，包括圆片、小棒、计数器等。

如一年级下册《青蛙吃虫子》一课中有这样的问题：大青蛙吃56只虫子，小青蛙吃30只虫子，一共吃多少只虫子？虽然许多学生在课前就会计算“56+30=86”了，但他们可能并不理解其中的道理。操作实物能帮助低年级的学生理解算理，即“5个10加3个10等于8个10，8个10加6个1等于86”。学生只有明白了这个加法算式的意义，才算真正懂得了两位数不进位加法的算理。

1.2  中高年级的算理型课堂

五年级下册《分数乘法》中有这样一道题：2个的和是多少？说一说列出×2的理由。解这道题时，学生会根据自然数乘法的意义推导出分数乘法的意义，把加法算式和乘法算式联系起来。在讲解这道题时，教师要告诉学生×2就是2个相加的和，也就是==。要帮助学生理解算理，完成从形象思维到抽象思维的过渡。

这一教学过程是从运算知识的源头帮助学生理解算理。教材中还有很多这样的算理型知识，包括两位数乘一位数的口算、表内除法等。

1.3  算理型课堂教学策略

在算理型课堂上，教师需要做到：①为学生创设合理的情境;②让学生操作不同实物或观察直观示意图，明白算式的意义，并对算理有深刻的理解;③对“运算意义”进行讨论和研究，为笔算方法的教学做铺垫。

2   算法型课堂

算法型课堂是指在算理的基础上构建运算法则的课堂。理解了算理，学生才能进行有效的知识迁移。计算方法是千变万化的，在理解算理的基础上，才能真正掌握运算方法。通过直观操作或观察理解算理，是为了摆脱实物的束缚，构建抽象的算法;也只有具备扎实的算理根基，才能更好地掌握算法。

2.1  低年级的算法型课堂

在三年级下册《分桃子》一课中有这样的问题：有6个篮子，每个篮子里有10个桃子，篮子外还有8个桃子，现在要将这些桃子平均分给2只猴子，求每只猴子分到多少个桃子？解這道题时，可以让学生结合已有的知识经验，利用小棒或实物图来理解题意，即6篮桃子平均分给2只猴子，每只猴子得3篮;剩下的8个桃子也平均分给2只猴子，每只猴子得4个。针对思维能力更高的学生，可以引导他们把68分成60和8，然后得出60÷2=30，8÷2=4，30+4=34。这两种方法实质上都是“6个10÷2=3个10;8个1÷2=4个1;3个10+4个1=34”。学生只有充分理解算理，才能在学习除法竖式法则时水到渠成。

2.2  中高年级的算法型课堂

在教学五年级下册《分数除法（一）》时，教师可以引导学生从除法的意义的角度理解算理。

问题一：把一张纸的平均分成2份，每份是这张纸的几分之几？

学生结合直观算法，利用分数的意义，把看成4个，平均分成2份，每份是2个，也就是，用算式表示为：。

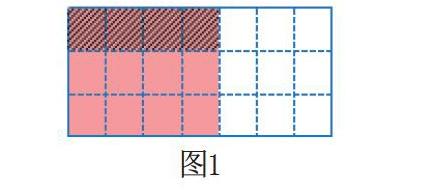
问题二：把一张纸的平均分成3份，每份是这张纸的几分之几？（如图1所示）

这两个问题是同构的，但是问题一中的被除数的分子是2的倍数，而问题二中的被除数的分子不是3的倍数。学生通过比较分析，找到了解决问题二的方法和思路：第一，借助面积模型，如图1所示，可以知道每份是的，也是整张纸的;其二，用算式记录直观运算的过程和结构，，进一步明确“平均分成3份”与“的”之间的关系。这沟通了分数除法与分数乘法本质的联系，为接下来的学习奠定了基础。

2.3  算法型课堂教学策略

在算法型课堂上，教师需要做到：①注重知识的迁移类推，调动学生的已有经验，突显运算意义;②运用多种方式帮助学生理解算理;③让学生对比、优化多种方式，内化计算法则。

3   算律型课堂

算律型课堂是在算法的基础上概括运算规律的课堂。小学涉及的运算律主要有加法交换律、结合律、乘法交换律、结合律和分配律。

俞正强谈到：算律其实就是算法的“窍门”。算法侧重答案，算律侧重速度。算律是对算法的熟能生“窍”。算律起源于算法的运用，因此算律的教学应该从算法的运用开始，进而观察概括出相应的规律。

3.1  中高年级算律型课堂

在教学四年级上册《加法交换律和乘法交换律》一课时，教师可以出示4+6=6+4和3×5=5×3两个等式，让学生通过观察算式，照样子写一写。给出这两个等式的目的是让学生进行类比推理和归纳推理，发现加法交换律和乘法交换律。学生经过观察，会发现等号两边算式的计算结果是相等的。此时教师不能急于给学生结论，而要让学生自己试着写出其他的加法等式和乘法等式，并进行验证。虽然学生自己写出等式，总结的语言可能不够规范，但学生自主发现问题、提出问题的过程是不可或缺的环节，能积累思维经验。最后，教师只要准确描述和即可。

随后，可以让学生寻找生活事例解释自己所发现的规律，直观感受运算律的客观存在，并用文字、图形、符号等形式表示这个算律的特征。这样能让学生找到学习数学的思路并积累探索规律的学习经验。

3.2  算律型课堂的教学策略

在算律型课堂上，教师需要做到：①引入计算情境，激活学生的思维与经验，直指运算方法;②根据算法，对大量的不完全归纳法素材进行整合;③让学生多元表征算律。

要提升学生运算能力就要将算理、算法和算律紧密结合。因为算律源于对算法的灵活运用，算法的建立是以算理为基础的。只有合理地将三者结合在一起，才能更好地提升学生的运算能力。

【参考文献】

[1]杨凯明.谈基于算理、算法和算律的三类计算课[J].小学数学教师，2017（10）.