基于多尺度空洞卷积的对抗去雾网络

（安徽大学 电气工程与自动化学院，安徽 合肥 230000）

引言

雾天情况下，由于光的折射与反射现象的存在，空气中的悬浮颗粒和小水滴将导致采集到的图像对比度降低、颜色失真并且细节模糊[1]。近年来，研究者们针对雾天搜集到的图像存在严重的质量降低问题，提出了非数据驱动[2-3]和数据驱动[4-6]的去雾算法。其中，非数据驱动的去雾算法依赖于先验假设或物理规律（比如大气散射模型）；数据驱动的去雾算法需要大量的有雾和无雾图像作为深度卷积神经网络的训练数据。本文提出的去雾算法为数据驱动算法，有效地利用了有雾和无雾图像数据包含的统计特性。

大气散射模型为去雾算法提供了研究的理论基础。He[2]针对有雾和无雾图像的像素规律提出了暗通道先验去雾算法，但是He 方法并不适合天空区域，去雾后的图像存在颜色偏移问题。Ma[7]结合Lab 空间和单尺度Retinex 设计了一种双边滤波优化的去雾算法，有效地避免了He算法存在的颜色失真现象。Sun[8]针对线性传输算法中大气光和透射率估计不准确的问题，设计了基于线性模型的自适应优化去雾算法。Zhu[3]通过统计有雾图像的颜色信息，提出了颜色衰减先验去雾算法，但是Zhu算法获得的去雾图像存在一定的细节模糊。Li[4]将深度神经网络与大气散射模型相结合，设计了AOD-Net（all-in-one dehazing network），但是Li 采用的网络结构较为简单，去雾后图像存在纹理模糊问题。Yu[9]提出了全局参数估计的偏振去雾算法，但是其应用场景限制在水下。Wei[10]将图像块的选择结合到去雾算法中，增强了系统的鲁棒性，但同时也增加了算法的计算量。Zhang[6]采用密集连接的生成对抗网络设计了端到端的去雾算法，但是该算法需要场景对应的深度信息作为监督，实际应用场景中获取较难。文献[11]同样采用生成对抗网络设计了去雾网络，但是此方法需要使用透射图作为训练标签，在实际应用中透射图的获取非常复杂且昂贵。本文提出的算法采用生成对抗网络，但是不需要场景对应的深度信息或者透射图信息，便于算法的实际应用。

本文针对现存去雾算法存在的细节模糊和颜色失真的问题，构建了基于多尺度空洞卷积的对抗去雾网络。网络采用空洞卷积作为特征提取模块，有效地提取有雾图像和无雾图像的语义特征。通过结合感知损失[12]和L1 损失，对去雾图像进行纹理和细节优化。

1 多尺度空洞卷积对抗去雾网络

1.1 多尺度空洞卷积模块

空洞卷积主要应用于图像分割任务[13]中，可以有效地增加卷积模块的感受野。图1中展示了本文提出的多尺度空洞卷积模块（简称DMS block，multi-scale dilated convolution block）的整体结构。对于空洞卷积计算来说，选取不同的空洞率（dilated rate）可以获得不同尺度的像素信息。为了在图像去雾过程中获取多尺度的空间信息，采用3种空洞率对输入特征图（feature map）进行处理，空洞率分别为1、2和3。DMS Block 首先将不同尺度的特征图进行空间拼接，使得输出特征图通道数为输入特征图通道数的3倍。然后，使用融合模块（fuse block）对拼接后的特征图进行通道降维，以保证最终输出特征图通道数和输入特征图的通道数相同。

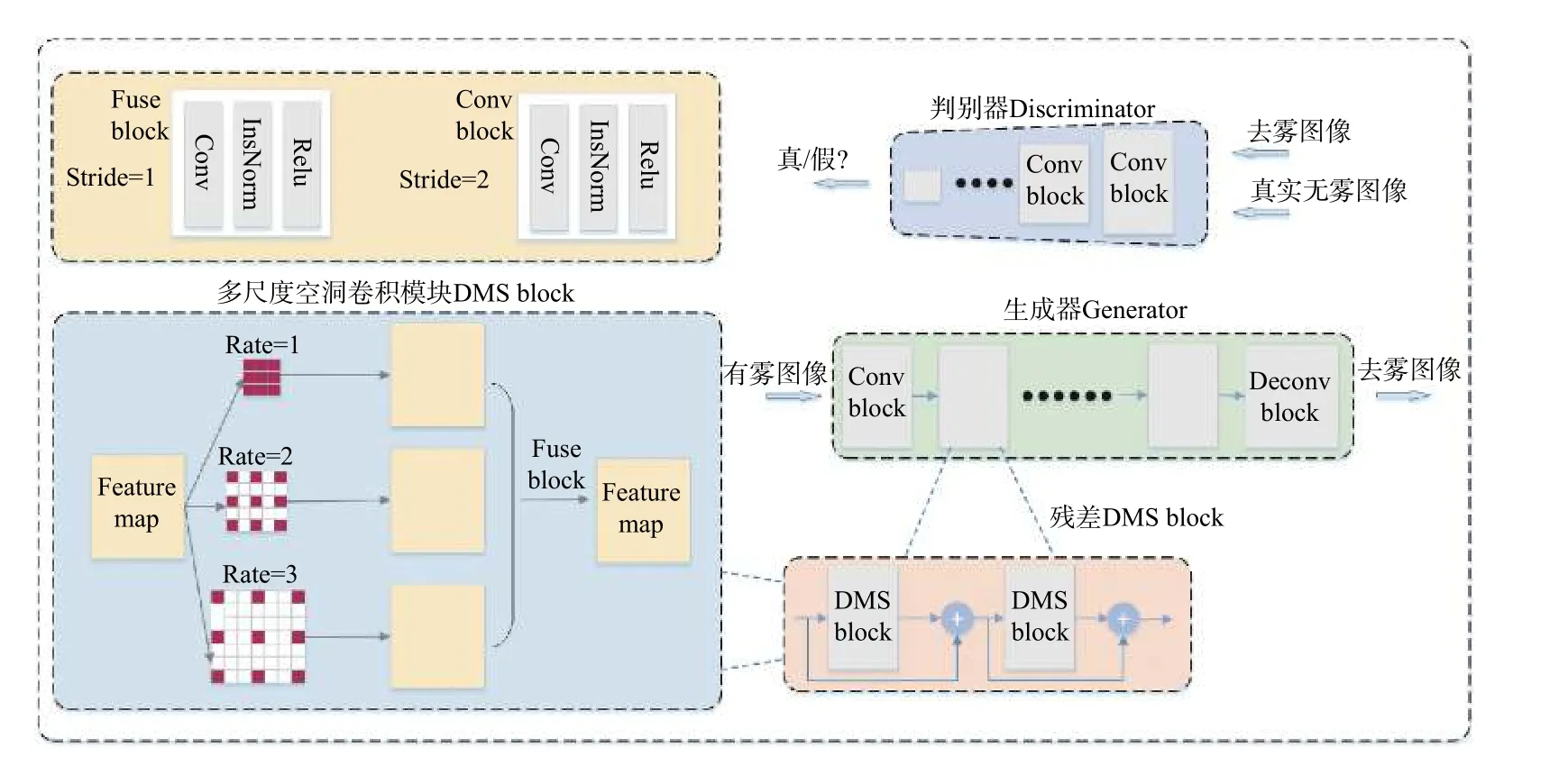
图1 整体网络结构图Fig.1 Structure diagram of overall network

1.2 去雾网络整体结构

本文提出的基于多尺度空洞卷积的对抗去雾网络包含一个生成器G（generator）和一个判别器D（discriminator），网络设计思路和原始生成对抗网络[14]（GAN，generative adversarial networks）相 同。生成器G负责去除图像中的雾，判别器D 负责区分去雾后得到的图像和真实无雾图像。

生成器G的输入为有雾图像，输出为去雾后的图像。通过梯度更新的优化过程，生成器G将学习到有雾图像到无雾图像的映射函数。生成器共包含6 层，第一层为卷积模块（conv block），通过对3个通道的输入图像进行卷积，获得64个通道的特征图。G的中间4 层均为残差多尺度空洞卷积模块（DMS block，），其中残差表示残差连接[15]。DMS block的结构如图1左半部分所示。通过选取不同的空洞率（Rate=1，2，3）可以获得不同尺度的特征图，将不同尺度的特征图使用融合模块（fuse block）进行空间融合，获得本层的输出特征图。生成器G的最后一层为反卷积模块（deconv block），其结构和图1左上部分的conv block 相同，区别在于使用反卷积替代卷积操作。

判别器D 由6个conv block 构成，输入为真实无雾图像和生成器G的去雾图像。判别器D为二分类器，用于区分真实无雾图像和去雾图像。

1.3 网络的训练过程

图像去雾算法采用有雾图像作为输入，通过对图像进行特定处理，获得最终的去雾图像作为输出。图1中展示了本文提出的多尺度空洞卷积对抗去雾网络的训练过程。首先将有雾图像统一缩放，获得像素尺寸为256×256的RGB 图像，并将像素值映射0到1之间，作为生成器G的输入，生成器G通过卷积模块以及多尺度空洞卷积模块对有雾图像进行卷积运算，随后生成器G输出像素尺寸为256×256的RGB 去雾图像。使用L1 距离计算去雾图像和真实无雾图像之间的像素差异，进行去雾图像的初步优化。采用感知损失计算去雾图像和真实图像之间的语义距离，通过优化感知损失获取更好的纹理和轮廓细节。

判别器D的输入包含两个部分：生成器G输出的去雾图像和真实的无雾图像。输入判别器D的所有图像像素尺寸均为256×256的RGB 图像。使用判别器D 对生成器G输出的去雾图像进行判别，实现网络参数的更新。

1.4 损失函数

原始的生成对抗网络[14]（GAN，generative adversarial networks）中，提出了最大最小博弈的目标函数，如下：

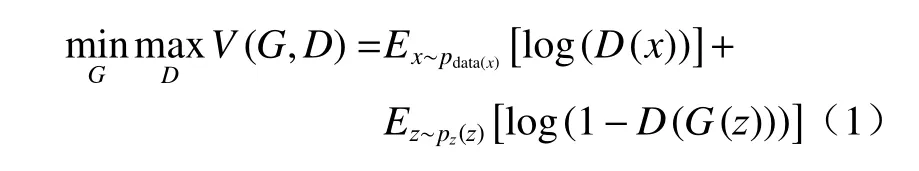
式中：x表示数据集中的图像；z表示噪声信号（可以从高斯分布或均匀分布中采样获得z）。本文提出算法使用有雾图像h替代原始生成对抗网络的噪声信号z，获得了如下的对抗性损失：

式中y*表示原始数据集中真实的无雾图像，对应于（1）式中的x。

感知损失[12]采用预训练模型VGG16[16]网络的前4个池化层进行特征计算，记VGG16 网络代表的映射函数为F。将去雾后的图像y输入到网络中，计算y与真实无雾图像y*的距离：

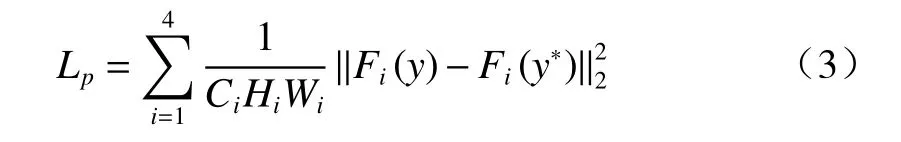
式中：i=1，2，3，4分别对应4个池化层的输出特征；Ci表示第i层特征图的通道数；Hi和Wi分别表示第i层特征图的高度和宽度。

此外，为了在像素层面对去雾后的图像进行像素层面的约束，采用L1 损失计算去雾图像y和真实无雾图像y*之间的像素距离：

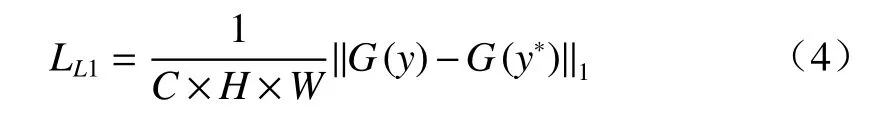
综上，生成器G和判别器D的总体损失函数为

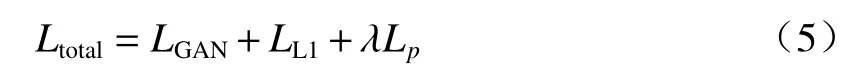
式中 λ为感知损失的权重，由于L1 损失和感知损失均对生成器G进行约束，所以可以固定生成器的L1 损失权重为1。通过调节 λ，控制生成器的L1 损失和感知损失的权重比例。2.3 节分析了感知损失权重不同时，网络去雾性能的变化情况。

2 实验结果分析

本文提出的去雾算法首先在训练集上进行参数训练，然后在测试集上进行定量评估指标计算。2.1 节介绍了峰值信噪比、结构相似性和色差3种评估指标；2.2 节和2.5 节给出了实验所用的2个数据集的具体信息以及对比实验结果，对比算法包括He[2]提出的DCP算法、Zhu[3]提出的CAP算法，以及Li[4]设计的AOD-Net算法；2.3 节对感知损失权重的选择进行了定量分析；2.4 节对比了不同迭代次数对应的去雾性能变化。

2.1 客观评价指标与实验设置

为了从定量的角度将提出的去雾算法与现存的算法进行比较，本文选择了图像去雾领域常用的评估指标：峰值信噪比（PSNR，peak signal-tonoise ratio）、结构相似性（SSIM，structural similarity index）和色差（CIEDE2000，commission internationale de l`eclairage delta）。

PSNR的单位为dB，其计算方式为

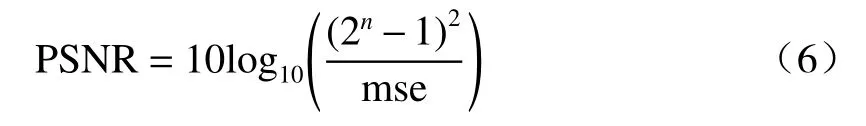
式中mse表示失真图像和真实参考图像的均方误差：

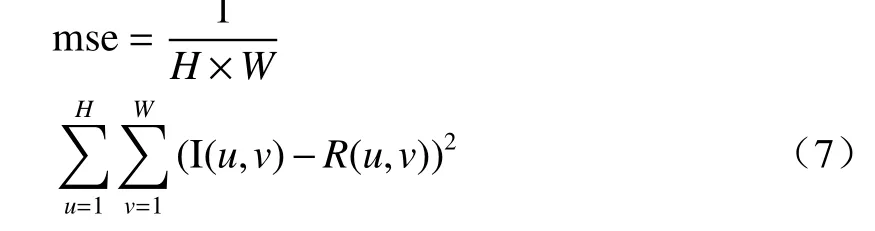
式中：I和R分别表示失真图像和真实参考图像；H和W分别表示图像的高度和宽度；u和v分别表示图像的像素横纵坐标。PSNR的值越高，表示图像中信号和噪声的比例越高，即图像恢复质量越好。

SSIM的取值范围在0～1之间，用以衡量失真图像和真实参考图像之间的结构相似性，值越大代表结构恢复性能越好。SSIM的计算较为复杂，具体过程见文献[17]。国际照明委员会于2000年提出了色差CIEDE2000（文中简称为CIEDE）评估指标。色差值越大表示图像的色彩失真越严重，具体计算过程见文献[18]。

对于提出的去雾算法，训练过程中学习率设置为0.0001，每次迭代采用的batch size为4，λ设定为4（分析见2.3 节），迭代次数设定为2 万次，2.4节对迭代次数选择进行了定量的分析。为了保证训练阶段的梯度计算和更新，通过裁剪和对齐将所有训练图像的长和宽均设置为256。测试阶段每次输入一张任意尺寸的图像，不需对图像尺寸做任何限制，直接输入生成器进行去雾。

本文在人工构造的公开数据[19]和自然场景拍摄的有雾数据集[20]分别进行了10次重复实验。实验中，为了排除训练过程带来的误差影响，将去雾算法和AOD算法分别进行10次重复实验，并计算对应评估指标的均值和方差；DCP和CAP算法不需训练过程，对于固定的输入其所获的输出也是相同的，因此可采用单次实验方式准确地获得实验结果，故不需计算方差值。此外，所有对比实验的参数均按照对应论文中提供的方案设置。

2.2 NYU-Depth 合成雾的实验结果

NYU-Depth[19]数据集包含精确标注的深度图，D-HAZY[21]提出在NYU-Depth的基础上结合大气散射合成有雾与无雾图像。本文采用D-HAZY的合成算法，合成了1449 对有雾与无雾图像。实验中，选择1149 对图像作为训练集，300 对图像作为测试集。

实验参数设置方式见2.1 节，表1提供了PSNR、SSIM和CIEDE的计算结果。从实验指标值可以看出，本文提出的算法获得了更高的峰值信噪比和结构相似性的值，并且具有最低的色差值，从定量的角度证明了提出的算法去雾性能较好。

表1 NYU-HAZE 结果Table1 Results of NYU-HAZE

雾的存在会降低图像对比度，并造成图像细节模糊。因此，需要从视觉效果角度对去雾算法进行评估。图2展示了本文提出的去雾算法与其他去雾算法的视觉结果。

从图中可以看出，DCP算法的去雾结果存在明显的颜色加深现象，同时存在较为明显的局部不完全去雾，原因在于DCP 没有准确地估计出大气光值和透射图。CAP算法能够较好地恢复图像的对比度信息，但是存在细节模糊的现象。AOD算法可以恢复图像的纹理和细节，但是会降低图像的对比度。本文提出的去雾网络能够完整地恢复图像的细节信息，并获得和真实无雾图像相近的对比度，证明了其结构恢复和对比度增强效果较好。

图2 视觉效果对比Fig.2 Comparison of visual effect

2.3 感知损失权重值的选择

为了研究感知损失项在生成器总体损失中占有不同权重时网络去雾性能的变化情况，实验中将 λ分别设置为2、4、6和8，同时保持网络其他参数设置不变，对本文提出的多尺度空洞卷积对抗去雾网络进行训练。表2展示了不同 λ值时对应的PSNR、SSIM和CIEDE值。从结果中可以看出，λ为4时所获的峰值信噪比和结构相似性值均较高，同时色差值较低，网络的去雾性能最优。

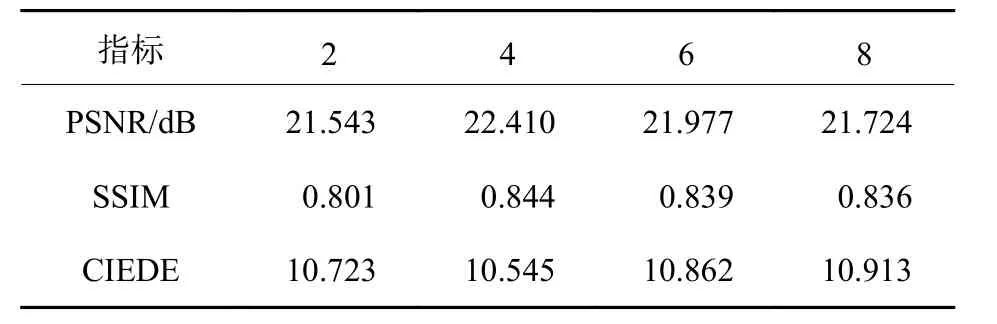
表2 λ对PSNR、SSIM、CIEDE的影响Table2 Impact of λ on PSNR，SSIM，CIEDE

2.4 最优迭代次数

迭代次数是深度神经网络算法的重要参数之一，迭代次数过多或者过少，都会导致模型表现不佳。通过2.3 节的分析，确定了感知损失权重 λ为4时整体去雾性能最好。通过固定感知损失权重值以及网络的其他参数，分别对不同迭代次数所获的去雾模型进行测试。图3、图4和图5展示了不同迭代次数对应的PSNR、SSIM和CIEDE值。从图中结果可以看出，训练的迭代次数为2 万次时获得的PSNR和SSIM值较高，同时CIEDE值较低，网络性能较好。

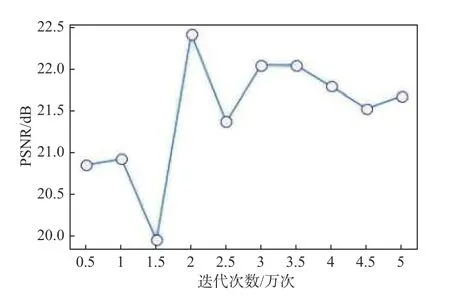
图3 迭代次数和PSNR值Fig.3 Iterations and PSNR value

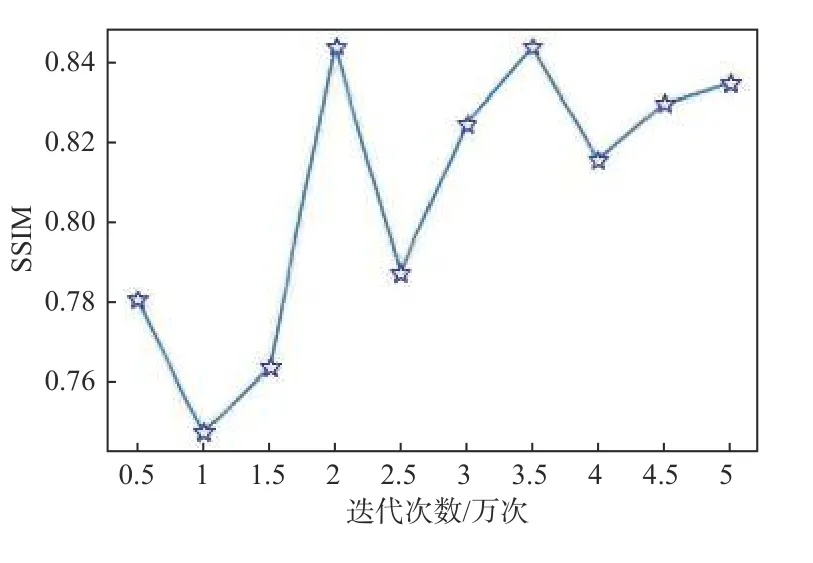
图4 迭代次数和SSIM值Fig.4 Iterations and SSIM value

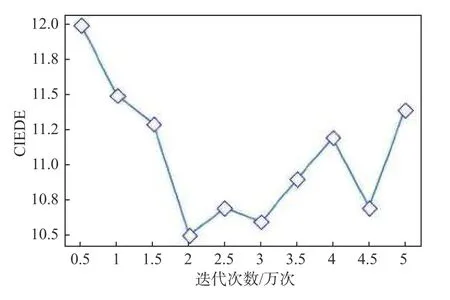
图5 迭代次数和CIEDE值Fig.5 Iterations and CIEDE value

2.5 O-HAZE 实验结果

深度神经网络需要充足的训练数据，在有雾图像成对和无雾图像较少的情况下，可能会影响最终的去雾性能。为了证明本文提出的算法在自然有雾应用中在数据量较少的情况下仍然能够获得清晰的去雾图像，选用包含室外图像的OHAZE[20]数据集进行定量和定性评估。O-HAZE包含45 对同一场景下拍摄的有雾图像与无雾图像。实验中随机选取35 对作为训练数据，10 对图像作为测试数据。表3中实验结果表明，本文提出的去雾网络能够获得更高的峰值信噪比值，有效地减少了雾产生的噪声信号；提出的去雾网络获得了最优的结构相似性值，保证去雾后的图像不会出现结构扭曲现象；同时，色差值最低，表明在室外有雾场景中恢复颜色信息的能力较好。

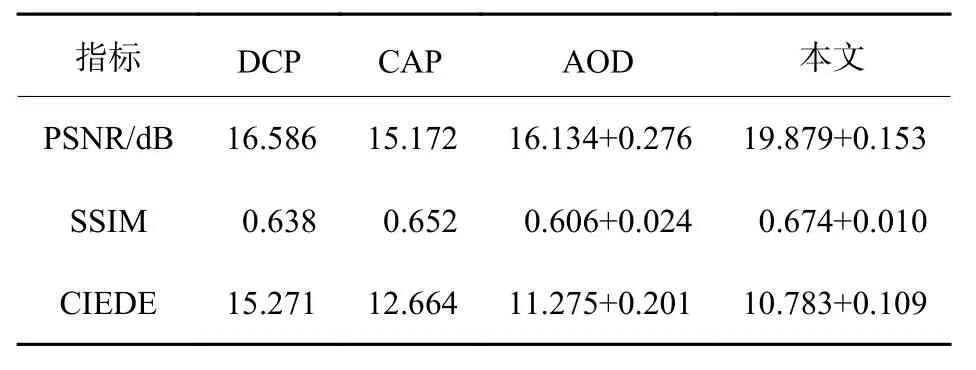
表3 O-HAZE 结果Table3 Results of O-HAZE

图6中给出了去雾算法的视觉效果对比，DCP算法和CAP算法存在较为明显的颜色失真现象，同时对于天空区域的处理结果较差。AOD 去雾算法所获的去雾图像细节较为模糊，去雾结果中仍然保留少量的雾块。本文提出的去雾网络通过多尺度的空洞卷积模块，充分地提取了有雾图像和无雾图像的特征，获得了清晰的去雾图像，并且去雾后的图像在天空区域不会出现颜色失真现象。同时，通过采用感知损失，增强了图像的纹理细节，保证去雾后的图像边界轮廓清晰。

图6 O-HAZE 视觉效果对比Fig.6 Comparison of visual effect on O-HAZE

3 结论

本文提出了基于多尺度空洞卷积的对抗去雾网络。生成器首先采用不同空洞率的空洞卷积模块进行特征提取，然后将获得的多尺度的特征图进行空间融合。去雾网络通过感知损失在特征空间对图像质量进行优化，增强图像的纹理信息和轮廓细节。实验结果表明，本文提出的去雾网络能够获得较高的峰值信噪比值和结构相似性值，并保证去雾后图像不存在明显的颜色失真现象。定量指标结果和定性视觉结果均证明了提出的算法具有较好的去雾性能。