债券信用利差影响因素分析——以企业债券为例

朱紫嫣，刘 蕾

（巢湖学院工商管理学院，安徽巢湖 238000

中国企业债券（Enterprise Bond）的发行始于1984年，最初是为了解决企业在发展中资金不足而向内部员工发行的具有特殊法律规定形式的债券。随着经济的发展，企业债券因其能较好地发挥财务杠杆作用，具有一定的抵税效应，逐渐演变成股份公司直接融资的重要工具。企业债券的发行上市与流通交易对于企业本身乃至整个债券市场都具有非常重要的意义。

纵观企业债券的发展历史可以发现，自1998年至2017年的20年间里，企业债券的发行量虽然在部分年份有所下降，但总体趋势在不断上涨，特别是2014年，债券的发行规模达到了6961.98亿元，发行次数高达583次。但与政府债券相比，企业债券由于没有国家信用做担保，还本付息依靠的是企业自身的盈利能力，存在一定的违约风险。2014年3月4日，深圳证券交易所公告确认，上海超日太阳不能按期支付前期承诺的票据利息。同年3月7日该债券兑现这一公告，正式违约，成为国内第一只违约的公募债券。此后，湘鄂债、珠海中富也出现违约现象，企业债券的违约现象层出不穷。因此，需要对企业债券的违约情况进行更为全面的评估。

文章以 2008年至2017年10年间发行的企业债券为研究对象，从宏观、微观以及企业债券自身的角度来研究企业债券信用风险产生的主要原因，以期能引导投资者更加审慎的投资，并促进债券市场的规范、有效、合理的运行。

一 文献综述

衡量企业债券信用风险的一个重要指标是债券信用利差，国外学者对其研究主要集中在以下几个方面：

一是对如何构建信用利差的模型进行研究。Merton（1974）提出了结构化模型，该模型是在B-S期权定价模型的基础上构建的信用风险定价模型。Merton认为，企业的违约风险与资本结构有关，资不抵债的可能性越大，信用风险越大。此后，Jones（1984）对结构化模型进行实证研究，认为该模型会低估企业债券的信用利差，并在此基础上提出了信用利差分解理论。也有学者将违约看作独立随机事件，服从强度为λ的泊松分布，并建立了简化模型。之后又引入信用评级因素，对模型进行了升级，使其更加合理化。但后来学者通过研究认为，简化模型在运用的过程中会存在参数不稳定的情况，所以在此基础上引入了税收、利率、流动性这些宏观因素以及企业性质等微观因素。

二是构建模型对信用利差的影响因素进行实证分析。如：Collin-Dufresne（2001）将宏观变量引入结构化模型，认为，基础利率、债券供应量等宏观指标对债券信用利差的影响更大。Hibbert（2011）通过模型验证，认为股权波动对债券信用利差有正的作用，且对信用评级较低的债券影响更为显著。

国内学者更多是运用国外的理论，构建实证模型，从宏观、微观以及单债券的角度对信用利差进行研究。李岚（2010）对中期票据进行研究，认为信用利差与十年国债到期收益率、中期票据月成交的频率、固定资产投资的同比增速、PMI以及M2和M1同比增速之差的变化之间存在负相关关系。戴国强、孙新宝（2011）基于Merton的结构化模型，以2000年2月到2010年9月上市的债券为研究对象，验证了宏观因素对企业债券信用利差的作用机制，并认为模型的解释力和债券的信用级别成反比关系。谢宇（2013）的研究实证检验了在结构化模型中，宏观因素对中期票据的信用利差解释力度较大，且显著性较高。任兆璋、李鹏（2006）以2004年6月30日为分析日期，计算18只债券的信用利差，并分别采用结构化模型和财务比率两种方法对信用利差个体影响因字进行分析，认为存在利差的最大原因是债券存在流动性不足的情况，并且认为财务比率方法比结构化模型更能解释中国企业债券存在信用利差的现象。周宏、建蕾（2016）通过对债券发行企业承担的社会责任进行实证研究，认为企业承担社会责任越多，债券信用利差越小，并且这一现象在民营企业中更加显著。

此外，张家琪（2017）在原有影响因素的基础上加入了工业增加值、国债利率结构等变量，构建VAR模型，实证检验了信用利差与工业增加值和国债利率差负相关。

本文基于上述理论，在选取企业各项财务指标的基础上引入宏观经济指标和单只债券的信用风险因素，构建多元回归模型分析影响企业债券信用利差的主要因素，以期能对投资者合理投资提供一定的建议。

二 究理论和研究方法

（一）信用利差的度量

1.信用风险。在企业债券市场上，投资者面临着各种难以预料的风险，如信用风险，赎回风险，利率风险，流动性风险等。其中：信用风险无疑是最主要最突出的风险。信用风险是指发行人到期日因无法及时或足额偿还债券本金和利息而使债券持有人遭受损失的风险。其与无风险债券相比，企业债券存在一定的信用风险。

2.信用利差。为了弥补投资者可能因为持有企业债券而承担的信用风险，债券发行人需要提供比无风险债券更高的收益率用来补偿这部分的损失。这部分损失，通常用信用利差来进行量化。投资者可以通过了解信用利差的大小来估计债券定价的高低，并且可以对影响信用利差因素的变化幅度进行研究和分析，用来判断该债券预期收益的变化，推测债券的信用风险，从而作出正确的投资选择。

（二）变量选取

由于2018年的宏观数据国家统计局尚未公布，本文选取2008年至2017年上市的企业债券，以GDP增长率、CPI增长率、M2增长率、财政支出增长率，无风险利率、Z变量，债券信用评级，债券剩余期限为变量对企业债券信用利差作相关分析并构建多元回归模型，进行实证研究。

（三）理论假设和变量定义

1.宏观因素。宏观经济对企业债券信用利差的影响主要源于宏观经济的发展水平及宏观政策。因此选择GDP增长率、CPI增长率、M2增长率、财政支出增长率及无风险利率为变量进行分析。

GDP是国民经济核算中的主要指标，是用来表示一个国家或地区经济的发展水平。GDP的波动幅度可以反映经济的宏观风险，波动幅度越大，风险越大，债券的信用利差越大。本文取企业债券发行当年（GDP增长率未搜集到月度数据，国家统计局也未公布货币供应量的月度和季度数据，为了保证数据之间的连贯性，本文选择了年度数据）GDP增长率的自然对数作为度量指标。

CPI是用来描述与居民生活相关的消费品以及服务价格水平变动情况的重要经济指标，也可以用来衡量社会的通货膨胀水平。一般而言，在居民总体收入水平一定的条件下，CPI增长率越高，通货膨胀率越高。但就近十年的经验数据来看，中国的通过膨胀现象并不严重。轻微的通胀会刺激投资，增加债券的需求量，信用利差增大。因此，假定二者呈正相关关系。同时在数据选取时，为了保证可比性，以企业债券发行当年的CPI增长率为依据进行计算。

国家的宏观政策包括财政政策及货币政策。中央银行货币供给量的增长会影响市场上的利率波动水平，从而会增加企业的系统性风险，最终导致债券信用利差的增大。因此，假设二者存在正相关关系。本文选取企业债券发行当年广义上货币供应量M2增长率作为衡量货币政策的主要指标。

与税收乘数的作用相比，政府财政支出的乘数效应更大，财政支出的增长能够刺激企业的投资，防范经营风险，降低企业债券的信用利差。所以，假定财政支出增长率与信用利差成反比关系。构建模型时以企业债券发行当年的财政支出増量率为度量指标。

与此同时，无风险利率也是影响企业债券信用利差的一个主要因素。一般而言，无风险利率上升时，宏观经济多处于经济周期的上升阶段，企业未来发展趋势越好，违约的可能性越小，信用利差也越小。因此，假定无风险利率与信用利差之间存在负相关关系。本文以与企业债券同期发行的一年期国债利率作为无风险利率的替代指标。

2.微观因素。美国学者Altman博士早在1968年就运用Z-Score指标来衡量企业的财务风险。该指标在运用的过程中主要是通过度量Z的值来判断企业的信用状况。Z值在1.81～2.675范围内时，与财务风险成反比关系。Z小于下限时为违约企业，大于上限时，则表示企业的信用状况很好。其具体模型是：

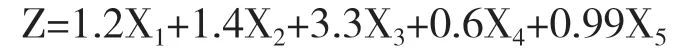
其中：X1=运营资产/总资产=（流动资产-流动负债）/总资产

X2=留存盈余/总资产=（股东权益合计-股本）/总资产

X3=息税前利润/总资产=总资产报酬率

X4=股东权益总额/总负债

X5=销售收入/总资产=总资产周转率

企业债券的主要风险是到期无法偿还投资人本金和利息所产生的信用风险，该风险与企业的财务风险挂钩，财务风险越大，信用风险越大。因此本文假定企业债券信用利差与Z值呈负关系。Z值中的所有指标均来源于企业债券上市前一年的财务报表。

3.单只证券因素。信用评级是专业的评级机构对债券的一个综合评价，这对发行债券企业的经营状况和信用偿付能力的判断。信用评级高的企业违约风险一般较小，相对而言票面率也会较低，信用利差较小。因此，假定信用评级与信用利差呈负相关关系。本文在此引入虚拟变量，赋值信用评级好的企业（发行时主体评级AAA）为1，其余企业为0。

此外，债券的剩余期限也是影响企业债券信用利差的主要因素。一般而言，企业债券剩余期限越长，未来不确定性越大，并投资要求补偿越高。所以假定企业债券剩余期限与信用利差正相关。

综上所述，本文选取的变量如下表1所示：

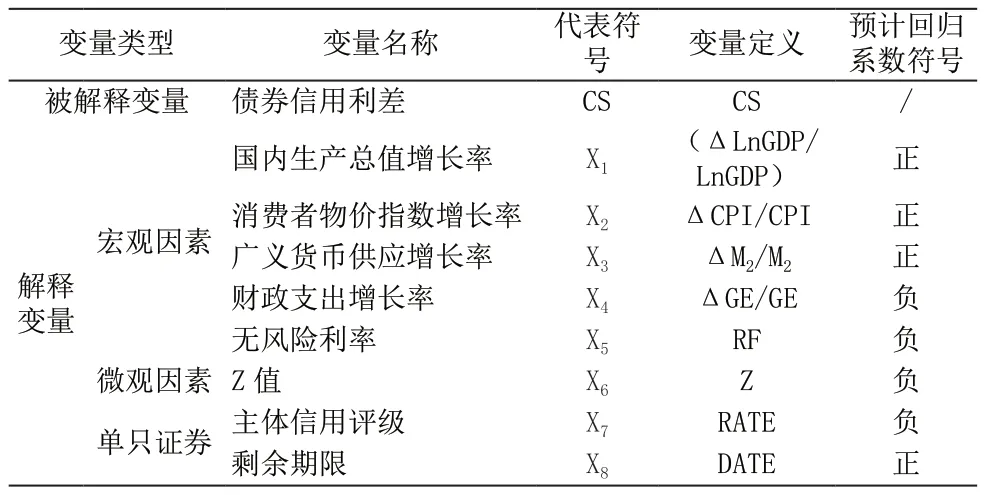
表1 变量的定义

三 实证分析

（一）模型构建

1.信用利差的度量。信用利差是指企业债券到期收益率与同期发行的国债到期收益率之间的差额。对信用利差的度量常见的有名义利差法、零波动利差法及期权调整利差法。本文考虑到数据计算的简便性和可收集性，采用的是名义利差法。

名义利差法是运用债券的到期收益和距离到期日剩余时间相同的国债到期收益率之差作为衡量的基础，计算公式如下：

上式中，P 是现行债券的市场价格，C Ft（t=1,2，……n）是债券第t年的现金流量，Tt表示现金流量的支付时间，根据已知条件可以求出企业债券的到期收益率R1。假设信用利差为CS，距到期日剩余时间相同期限的国债到期收益率为R2，则企业债券信用利差的计算公式为：

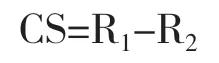
为了更好地选用混合横截面数据，构建回归模型。本文选取的为债券发行时的R1到期收益率，R2为同一期发行的相同期限的国债到期收益率。

2.多元回归模型的构建。根据前述的假设，现以表1中的变量构建一个多元回归模型，用来解释不同公司债券发行时的信用利差影响因素，具体模型如下：

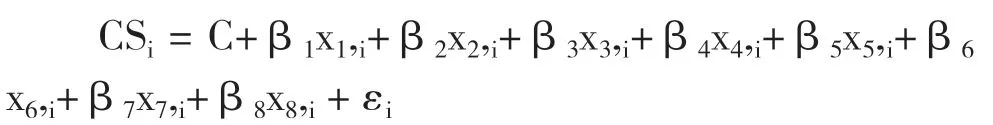
其中：CSi是被解释变量也即企业债券的信用利差，下标i表示在2008-2017年间发行的第i只债券，取值为1-80。C为常数项，为回归系数，（k=1,2,……8）为解释变量，代表第i只债券对应的影响因素指标。εi为模型的残差。

（二）数据来源及样本选择

本文宏观数据来源于国家统计局和英为财情网站，微观和单只债券数据取自Wind经济数据库。在样本选择方面，为了保证数据的完整性和客观性，剔除了含权债券、浮动利息债券、次级债券、混合利息债券、城投债以及一些数据不完整的债券，选出符合要求的80只债券，且该80只债券在分析信用利差时仅以发行时的数据为研究对象。

（三）模型检验

根据前述分析结果，构建多元回归模型，运用EVIEWS7.2软件对数据进行回归，得出结果如下表2所示：

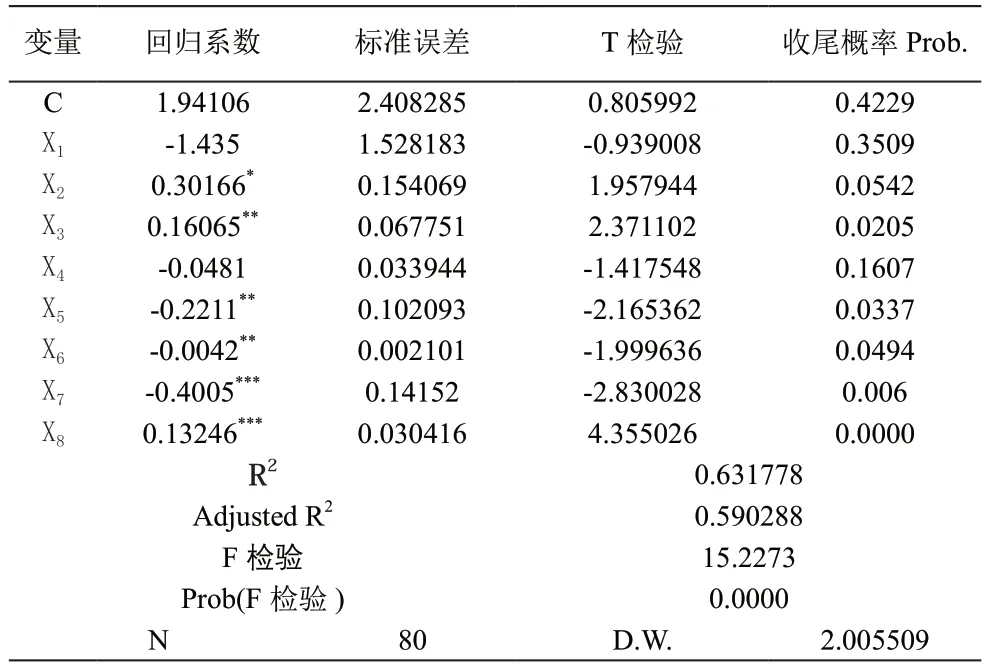
表2 多元回归模型实证结果1

从上表2中的回归结果可以看出，F检验的值为15.2273，P值为0.000，表明信用利差CS与自变量Xk有显著的线性关系。R2和调整后R2的值分别为0.631778和0.590288，整体拟合优度较好。但在单个变量的T检验中发现常数项C、国内生产总值增长率（X1）、财政支出增长率（X4）这三个指标的收尾概率大于显著性水平10%，表明变量未通过检验。

其实，在构建多元回归模型前需要对各个变量进行多重共线性分析，但考虑到不同变量的显著性差异，因此本文选择先构建模型，再进行共线性检验。运用软件分析后得出如下表3的结果：

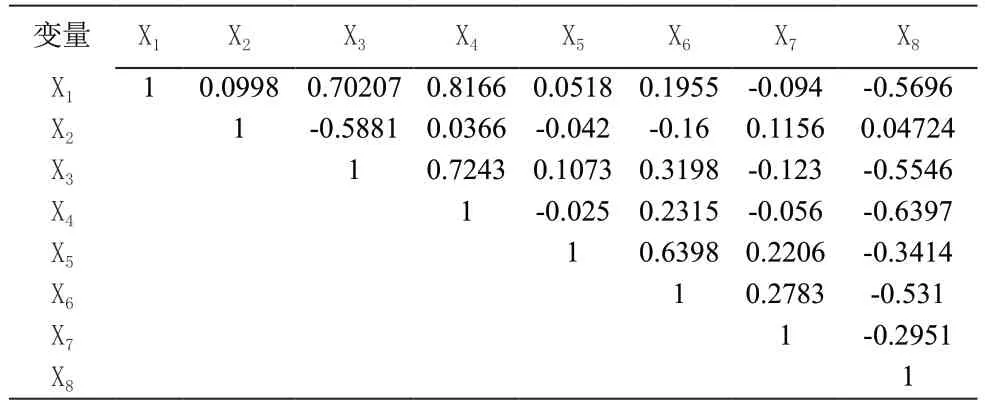
表3 多重共线性结果一览表

一般而言，相关系数的取值在0.8以上表明两个变量之间存在强烈的相关性，0.5-0.8则为中度相关，0.3-0.5为轻度相关，系数在0.3以下为基本不相关。表格中国内生产总值增长率、财政支出增长率、剩余期限与多个变量之间存在较高的相关性。并结合未通过T检验的变量，采用逐步回归法一一剔除相关性较高国内生产总值增率、财政支出增长率。得到表4回归结果：

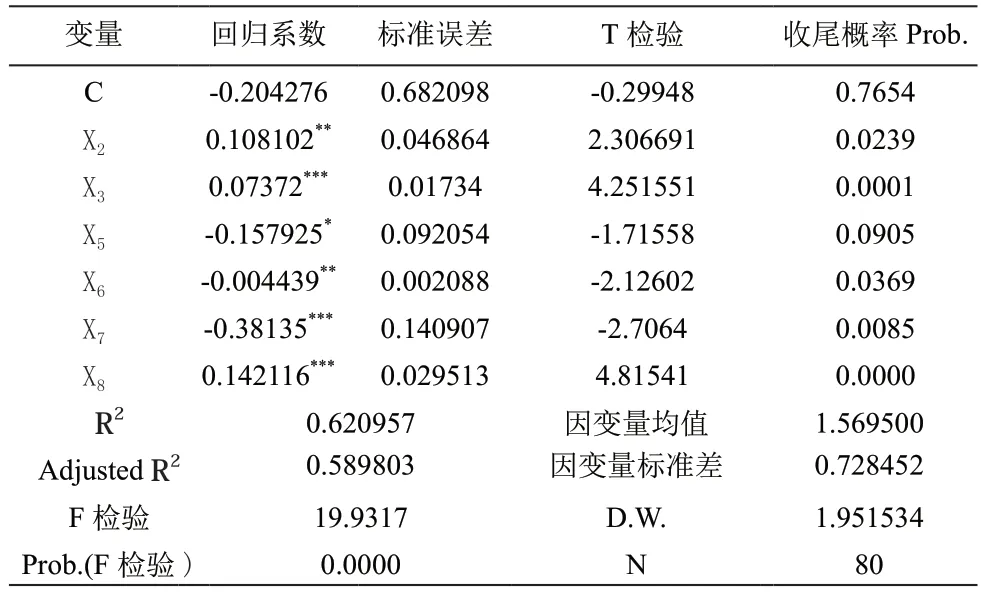
表4 多元回归模型实证结果2

剔除部分变量后，模型仍然可以通过F检验，R2和调整后R2的值较之前虽然有所下降，但影响不大，拟合优度效果依然较好。D.W.值为1.951534。经查表可知，在自变量为6，样本量为80的情况下临界值d1=1.36，du=1.62。因1.36＜D.W.＜2.64，所以基本可以判断，模型不存在自相关。T检验中，除无风险利率（X5）在10%的水平上显著外，其余变量均在5%的水平上对企业债券信用利差影响显著。但Eviews中T检验的收尾概率是双边检验的结果，一般只能判断原假设βi是否等于0的显著性，不能判断回归系数的正负。因此需要运用P值法对βi进行单边检验（职桂珍，2011）。本文为了得到更准确的回归系数符号，现据前述假设进行单边检验，因单边检验中的原假设一般包括等于零的选项，而备择假设无需考虑，所以对通过检验且前述预测回归系数为正的变量进行右边检验，预测的回归系数为负的变量进行左边检验。两种检验结果均能得出有效结论。

右边假设的原假设为：Ho:βi≤0；备择假设H1:βi＞0，置信区间α=0.05；左边假设的原假设：Ho:βi≥0；备择假设H1:βi＜0，置信区间α=0.05。经计算可得到如下表5结果：

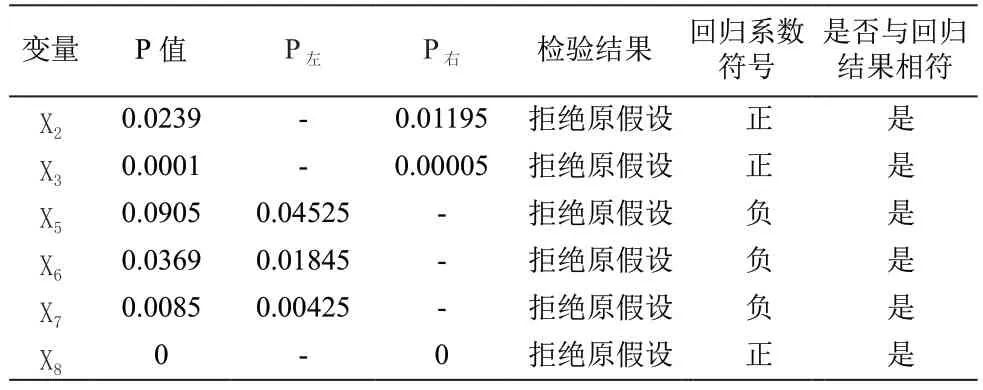
表5 单边检验结果一览表

因X2，X3，X8，右边检验的P右值小于置信区间0.05，因此拒绝原假设，接受备择假设。所以β2，β3，β8，即回归系数的符号为正。X5，X6，X7，左边检验的P左值小于置信区间0.05。同样拒绝原假设，接受备择假设。β5，β6，β7，都小于零，回归系数的符号为负。与前文预测一致。具体检验结果为：

1.宏观因素方面。消费者物价指数增长率的回归系数为正，且在5%的水平上显著，与预期假设一致，表明该指标对信用利差有正向影响，即消费者物价指数增长率越高，信用利差越大。广义货币供应增长率前的回归系数为正，单边检验的概率为0.00005，与假设相符，即该增长率越大，债券信用利差越大。此外，无风险利率前的系数符号也与前述假设一致，且在10%的水平上对CS影响显著。这就说明无风险利率越高时，经济发展趋势越好，债券违约风险越小，信用利差越小。

2.微观因素方面。Z值是一个反映企业风险的综合指标，从前述分析结果可知，Z值前的回归系数为负，收尾概率为0.0369，与预期假设相符。这就说明Z值对信用利差有反向影响的作用。也就是Z值越大，企业的财务风险越大，信用风险越大，信用利差越小。

3.单只证券方面。从单只债券层面对信用利差进行分析后发现，主体信用评级和剩余期限均在1%的置信水平上对信用利差有显著的影响。发行时债券的主体信用评级前回归系数为负，剩余期限回归系数为正，均与预期假设相符，表明主体信用评级越高，剩余期限越短，债券的信用利差越小。

此外，多元回归模型中还需要进行异方差的检验，现将前述变量进行怀特检验后得到如下结果：

表6 模型异方差检验结果

从上表5中可以观测到，怀特检验的统计量LM的值为67.43122，收尾概率远小于显著性水平1%，因此拒绝原假设，残差存在异方差。为了缓解异方差对模型的影响，本文采用怀特修正法来对模型的异方差进行修正。得到如下表7的结果：

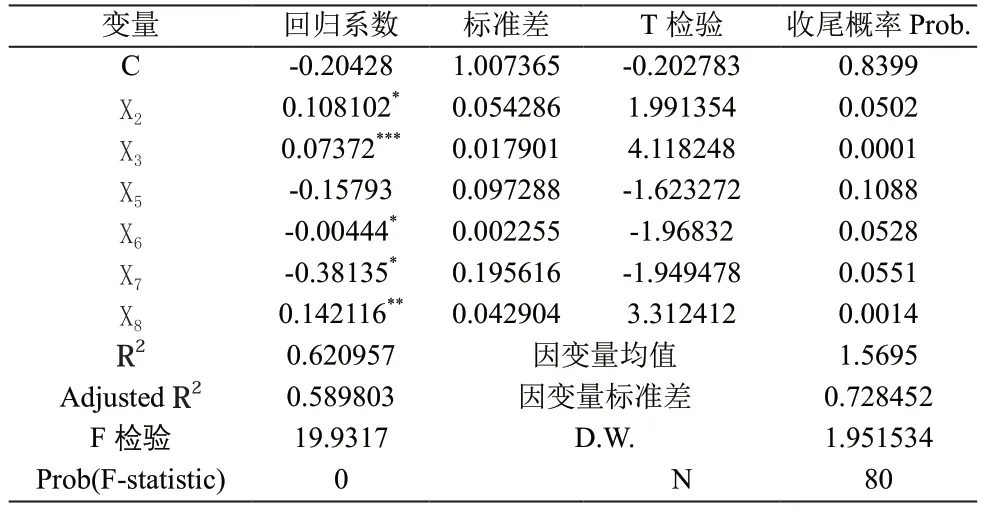
表7 异方差修正后检验结果

在表7中，虽然参数的估计量与OLS的估计量没有区别，但其标准差和方差有明显的变化。可以使以估计量方差为基础的统计量不再失效，预测区间更加可信。而T检验的收尾概率也发生了变化，都有所上升，其中无风险利率的概率变得不太显著。

（四）小结

对信用利差影响因素进行研究对促进债券市场的繁荣与发展有着重要的作用。本文构建多元回归模型，消除多重共线性和异方差的影响后得出结论：宏观经济因素中的CPI增长率、广义货币增长率，微观中的Z值和单只证券中的主体信用评级及剩余期限对信用利差影响显著且回归系数与前述假设一致。此外，无风险利率T统计量不够显著，GDP增长率，财政支出增长率未通过T检验。

四 对策建议

根据前述分析结果可知，若要进一步降低企业债券信用利差，需要从宏观的制度、微观的单只债券的角度进行完善。第一，应当稳定经济发展，保护投资者的利益。宏观经济的稳定对于降低企业的信用风险具有极大的促进作用。我国应实施相对稳定的经济政策，促进经济平稳运行，降低债券信用利差，保证投资者的利益。第二，提高经营能力，降低财务风险。企业的财务风险对信用利差的影响较为明显，债券的发行主体应努力提高自身的经营能力，吸引更多的投资者，降低企业的融资成本和财务风险。第三，构建完善的信用评级制度。对投资者而言，债券的信用评级具有非常重要的作用,并具有判断债券风险、了解发行主体和引导投资等功能。现阶段债券的信用评级虽然主要集中于中高等级，但违约现象仍然层出不穷，这表明信用评级存在虚高的情况。因此需要完善信用评级中介机构制度，加紧跟踪评级的方式和方法，共同促进债券市场的合理运行。

本文虽然对企业债券信用利差的影响因素进行了较为详实的分析，但也存在一些不足。如数据收集方面未充分考虑月度因素以及时间序列对利差的影响。此外，该结论是否适用于城投债等其他债券，需要进行更深层次的研究。