燕尾榫约束古建木梁环境温度效应试验研究

白晓彬，杨娜，常鹏

（1. 北京交通大学 土木建筑工程学院，北京100044；2. 中冶建筑研究总院有限公司，北京100088）

古建筑木结构在长期服役过程中，内部结构会出现大量的残损现象[1]，而环境温度和湿度的变化均会影响木结构的变形.环境温度对木结构变形的影响主要体现在材料的热胀冷缩效应、弹性模量变化、边界条件的变化及由此在结构中引起的附加次应力的综合.Bai 等[2]在对某古建筑的长期监测中发现，木构件的应变和温度高度相关，温度是影响结构变形的重要因素.王阳[3]对木材的顺纹方向热膨胀系数进行了研究，认为温度变化对木材顺纹方向尺寸变化的影响不可忽略.Green 等[4]根据试验提出了木材弹性模量和温度之间关系的公式，弹性模量随温度的升高而降低.Yarnold 等[5]在对桥梁的长期监测研究中认为温度变化可引起结构边界条件的变化，从而影响结构的变形.环境湿度对木结构变形的影响主要体现在木材的干缩湿胀，湿度变化会引起木材含水率的变化，从而引起木材尺寸和体积的变化[6].木材的干缩湿胀主要体现在横纹方向，而顺纹方向干缩湿胀相对较小[7].已有研究表明[8]，在拉萨地区一年之中七八月份湿度对木结构应变的影响不可忽略，而其他月份可只考虑温度作用而忽略湿度的影响.因此本文中的试验研究避开了七八月份，用其他月份的试验数据来研究温度效应的影响.

对于静定结构，环境温度对材料所产生的热缩效应可得到释放，结构只产生应变而没有应力；对于超静定结构，由于多余约束的存在导致材料的热缩变形无法得到释放，从而产生温度应力[9].榫卯连接作为我国古建筑木构件之间一种常用的连接形式，具有明显的半刚性特征，属于超静定结构[10].榫卯节点的类型有燕尾榫、直榫、馒头榫等，而燕尾榫是应用最为广泛的一种节点，也最具代表性.燕尾榫的榫头内窄外宽，卯口内宽外窄，抗拔性能好，使结构具有较强的整体性.目前有关燕尾榫节点的研究大都集中在其力学性能和抗震性能方面[11-14]，对木构件环境温度作用下的变形及环境温度变化对燕尾榫刚度的影响研究较少.

本文以燕尾榫连接的古建木梁为研究对象，在拉萨室内布置了一根无约束木梁和一根燕尾榫约束梁，分别对两根梁进行了空载和分级加载试验，研究环境温度效应下木梁顺纹方向的变形特征.根据试验数据，考虑环境温度的影响，对木材顺纹方向弹性模量、燕尾榫拉压刚度、转动刚度进行识别，分析了约束条件、上部荷载等因素对木材顺纹方向应变的影响，并对附加应变进行了理论计算.

1 试验概况

燕尾榫常用于水平构件与垂直构件的相交处，如图1 所示.在藏式古建木结构中燕尾榫也用于梁与梁之间的连接[15].在荷载作用下，燕尾榫节点可以承受一定的弯矩，且具有抵抗水平推力的作用.根据燕尾榫的构造及受力特点，可将燕尾榫连接的古建木梁简化为如图2 所示力学模型.燕尾榫的转动刚度为Kr，拉压刚度为Ks，梁承受上部均布荷载q.

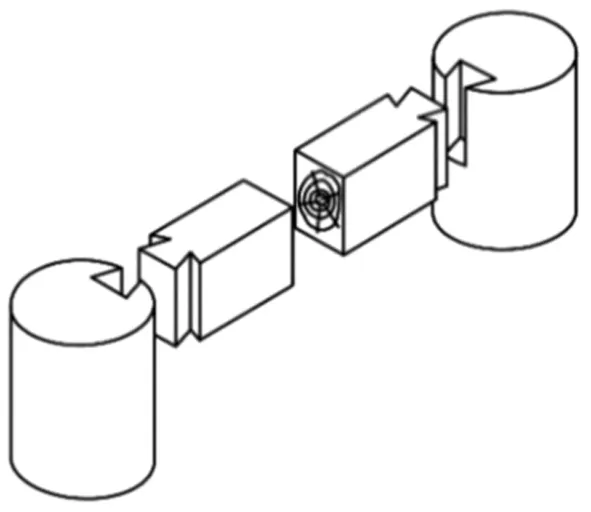
图1 燕尾榫节点示意图Fig.1 Sketch of moritise-tenon joint

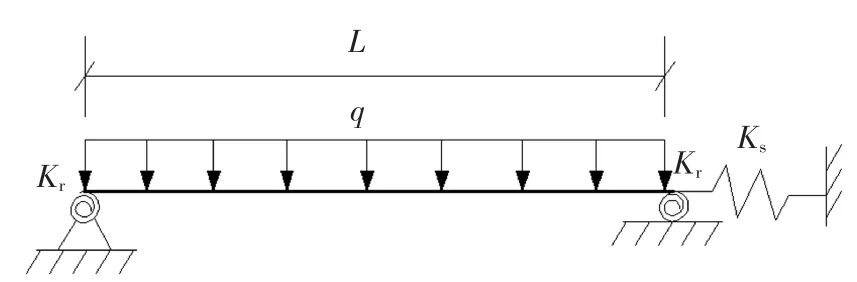
图2 木梁的简化力学模型Fig.2 The simple mechanical model of the timber beam

试验所用木材为松木，天然干燥期5 年以上.试验地点位于拉萨，拉萨全年降水很少，全年木材平衡含水率均值较低，仅为8.6%，且起伏较小，故可认为在试验期间木材含水率保持恒定.试验共制作两个试件，包括一个无约束的梁试件a 和一个木框架试件b，如图3 所示.

图3 试验试件Fig.3 Specimens of the experiment

图3 中，试件a 的两端直接搁置在两个木块之上，在接触部位抹润滑油，减少接触面摩擦的影响，不施加任何额外约束；木框架试件b 中的梁两端与两根短木柱以燕尾榫相连，木柱底部嵌固在木板中，将木板固定在地面上，以此来限制短柱的横向变形，为梁提供可靠的约束.两个试件中梁的尺寸均为：b×h×l=106 mm×126 mm×975 mm.

在两根梁的底部跨中位置各安装一个光纤光栅式应变计，测量梁的顺纹方向应变；在室内布置一个光纤光栅式温度计，测量环境温度，试验的采样频率为每小时采集一次.通过试验研究环境温度变化、边界条件和上部荷载等因素对梁底部跨中顺纹方向应变的影响.

试验分两个阶段进行，分别为空载阶段和加载阶段，试验的时间均避开了湿度影响较大的七八月份. 空载阶段的时间为2015-12-13—2016-06-30，此阶段两个试件上不施加任何荷载；加载阶段的时间为2016-09-16—2016-10-15，此阶段用红砖在两根梁上分别施加三级均布荷载，三级荷载的大小分别为q1=0.41 N/mm、q2=0.82 N/mm、q3=1.23 N/mm，在加载的1 h 内将采样频率提高至5 次/min，待变形稳定后再降至每小时采集一次.每级荷载的加载时间为一周，图4 所示为木构架的加载情况.

图4 约束梁加载图Fig.4 Loading of the restrained beam

2 木梁的参数识别

根据图2 中的简化力学模型，木梁的未知参数包括：木材的顺纹方向弹性模量E、燕尾榫的拉压刚度Ks、转动刚度Kr.通过试验数据和理论推导，对这些未知参数进行识别.

2.1 顺纹方向弹性模量的识别

顺纹方向的弹性模量E 通过无约束梁的试验数据进行识别.无约束梁在均布荷载下的跨中弯矩可按简支梁计算，即：M0=ql2/8.弯矩引起的梁底部应变为：

则在均布荷载作用下木梁顺纹方向弹性模量的计算公式为：

考虑环境温度变化对木材弹性模量的影响，温度越高，弹性模量越小.木材的弹性模量随环境温度变化的公式为[4]：

式中：ET为当环境温度为T 时木材的弹性模量；E0为参考弹性模量，一般取23 ℃时的弹性模量.

三次加载时刻的环境温度分别为22.2 ℃、23.6℃、22.9 ℃，可近似认为每次加载时的环境温度均为23 ℃.图5 为无约束梁三次加载前后的应变曲线，三次加载时应变分别增加了23.8με、25.2με、24.8με.则每施加一级荷载应变平均增加24.6με，即q=0.41 N/mm，Δε=24.6με，由公式（2）可求得，木材在23 ℃时的弹性模量E0=7 061.1 MPa. 根据不同时刻的环境温度值，可计算相应的弹性模量，图6 为2015-12-13—2016-06-30 的环境温度和弹性模量的变化曲线，二者成反比.

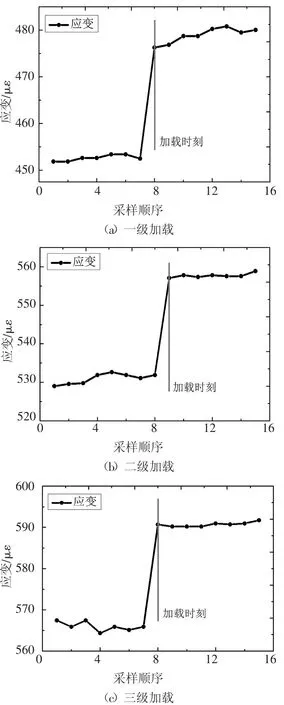
图5 无约束梁三次加载应变增量图Fig.5 Strain variations of every loading for unrestrained beam

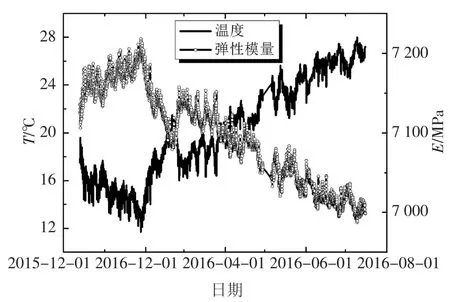
图6 环境温度和弹性模量曲线Fig.6 Curves of temperature and modulus of elasticity

2.2 燕尾榫拉压刚度的识别

燕尾榫的拉压刚度Ks应用空载试验的数据进行识别.当环境温度发生变化时，设无约束梁的应变为Δε1，约束梁的应变为Δε2，拉压弹簧会抑制约束梁的自由变形.以温度升高时的情况为例进行分析，当温度升高时，约束梁的位移平衡如图7 所示.图中δT为梁自由伸缩时的位移，δU为梁在约束下的实际位移，δR为约束位移，P 为梁端反力. 温度升高时P为压力，温度降低时P 为拉力.约束梁的位移平衡方程为：

将式（4）用力学模型中的参数进行表示：

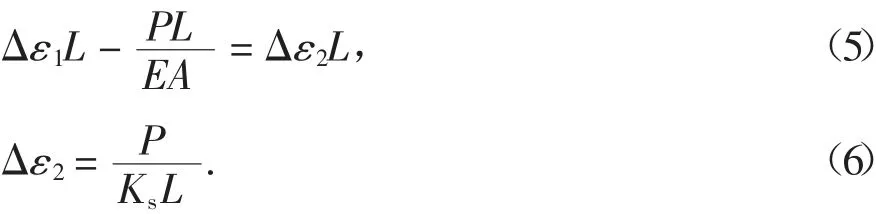
由式（5）和式（6）可求出Ks：

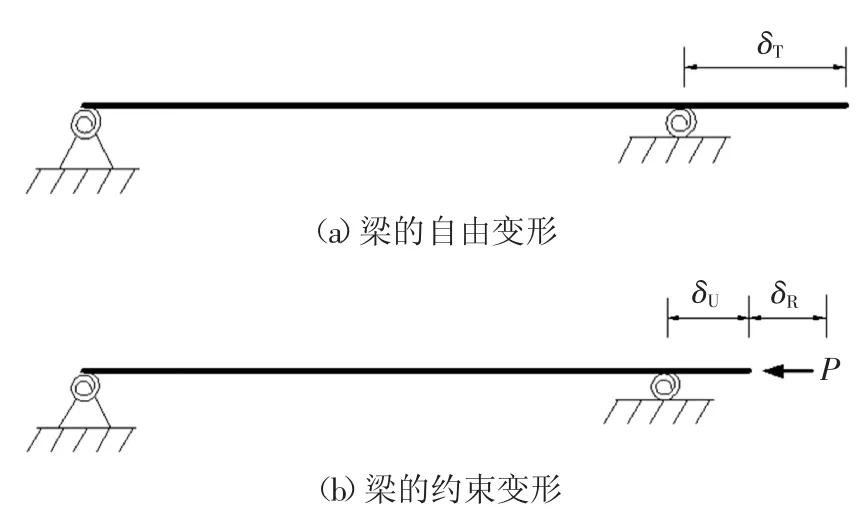
图7 梁的位移平衡图Fig.7 Nonlinear spring definition

燕尾榫的拉压刚度Ks的大小与两根梁在空载时的应变比值有关.对于燕尾榫而言，当温度升高时榫头和卯口为顺纹受压，温度降低时为斜纹受拉，所以升温和降温时的Ks是不同的，应分别求解升温段和降温段对应的应变比值.

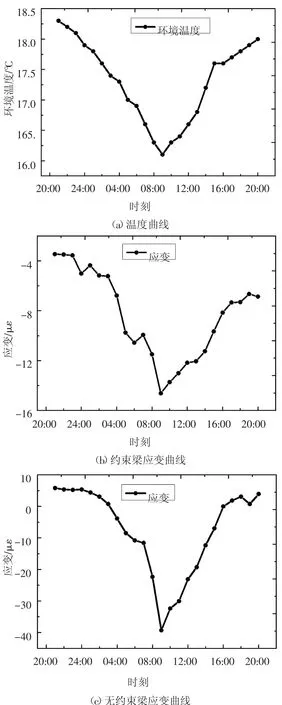
图8 24 小时数据曲线Fig.8 Data curve for 24 hours

根据试验数据，环境温度在1 d 内可分为升温段和降温段，以2015-12-14-21：00—2015-12-15-20：00 的24 个数据为例进行分析，1 d 内的温度曲线、约束梁和无约束梁的应变曲线如图8 所示，梁的应变和环境温度的变化趋势一致.其中第一天21：00 至第二天9：00 为降温段，共13 个数据，环境温度和梁应变均逐渐减小；9：00 至20：00 为升温段，共12 个数据，环境温度和梁应变增大.降温段和升温段的应变数据分别分析，并将每段的第一个数据设为0，其他数据均为相对于第一个数据的应变增量，两段的应变增量数据对比如图9 所示.图9 中无约束梁的应变均大于约束梁的应变，因此式（7）中的比值Δε1/Δε2应大于1.根据图9 的应变增量计算1 d 内升温段和降温段的应变比值，由于每段的第一个数据为0，故升温段可计算出11 个比值，降温段计算出12个比值，1 d 内的应变比值的曲线如图10 所示.依次计算每天的应变比值，并去除其中的异常比值，7 个月内升温段和降温段的比值曲线如图11 所示.取其平均值，升温段应变比值为2.25，降温段应变比值为1.72.根据式（7），可求出升温段和降温段的Ks曲线，如图12 所示.升温段的榫卯拉压刚度大于降温段，这是由于升温时卯口顺纹受压，而降温时斜纹受拉，二者受力状态不同.

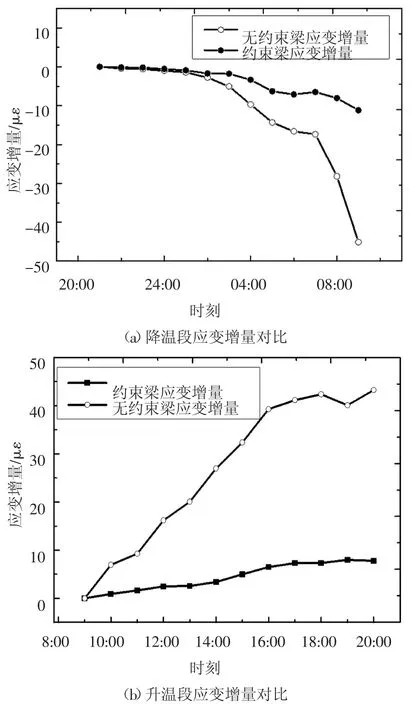
图9 应变增量分段对比Fig.9 Comparison for strain variations

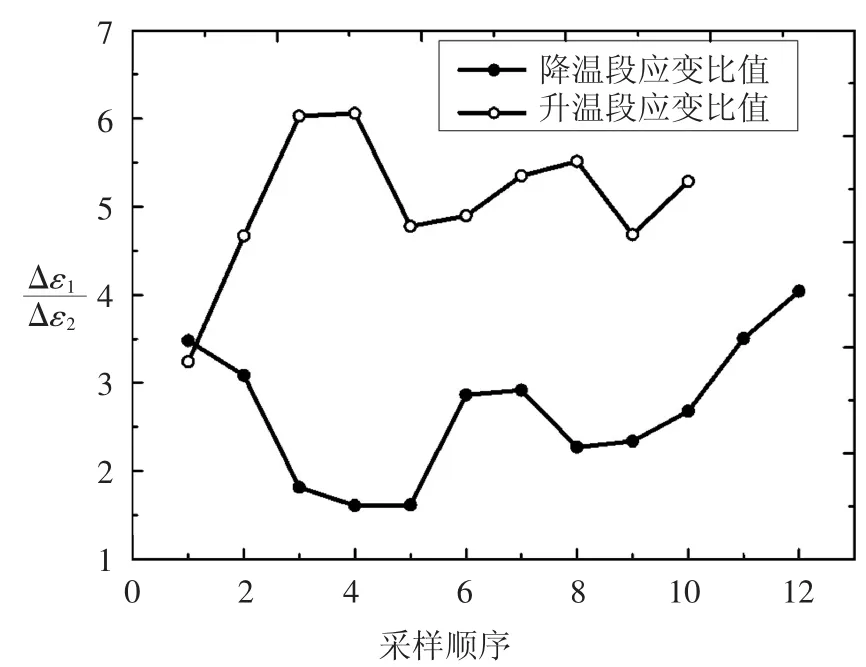
图10 一天内的应变比值Fig.10 Strain ratio in one day

图11 七个月应变比值Fig.11 Strain ratio in seven months

图12 拉压刚度曲线Fig.12 Curve of tension and compression stiffness

2.3 燕尾榫转动刚度的识别

燕尾榫转动刚度应用试件b 的加载试验数据进行识别.在荷载作用下，半刚性约束梁的弯矩介于铰接和固结之间，其底部跨中弯矩的公式为：M0=aql2（1/24＜a＜1/8）.图13 所示为约束梁三级加载前后的应变曲线，每增加一级荷载，其应变平均增加21.8με.根据式（1），可计算出a=0.11，即约束梁的底部跨中弯矩为：M0= 0.11ql2. 则约束梁的梁端弯矩为：MA=-0.015ql2.

图13 约束梁三次加载应变增量图Fig.13 Strain variations of every loading for restrained beam

半刚性约束梁的梁端弯矩计算公式为[16]：

图14 转动刚度曲线Fig.14 Curve of rotational stiffness

3 荷载作用下的应变分析

环境温度变化会引起木构件的伸缩变形，当梁端存在约束时，温度效应会在梁端引起支座反力.木梁在上部荷载作用下会产生一定挠度，故支座反力会对梁底部产生二阶弯矩作用，从而引起附加应变.本节通过试验数据对比分析约束条件、上部荷载对梁底部应变的影响.

3.1 空载段的应变分析

空载试验的时间为2015-12-13—2016-06-30.将试验的初始应变设为0，作出约束梁和无约束梁的应变增量对比，如图15 所示.约束梁与无约束梁的应变均先减小后增加，与图6 中温度增量的趋势相同，与温度增量的相关系数分别为0.7 和0.8，相关性较强.在温度变化相同的情况下，无约束梁的应变增量明显大于约束梁的应变增量，说明燕尾榫约束抑制了梁的自由变形.

3.2 荷载作用下无约束梁的应变分析

每级荷载的作用时间为一周，分析环境温度变化相同时，不同荷载对应变的影响.分别在空载和三种荷载工况的数据中各挑选环境温度变化相似的一个循环（从第一天21：00 到第二天20：00 的数据为一个温度循环），并将每个循环的第一个数据设为0，得到24 h 内温度增量和应变增量的对比曲线，如图16所示.从图中可看出：当温度增量相同时，无约束梁的应变增量也基本相同，这说明上部荷载的变化对无约束梁的应变增量没有影响.

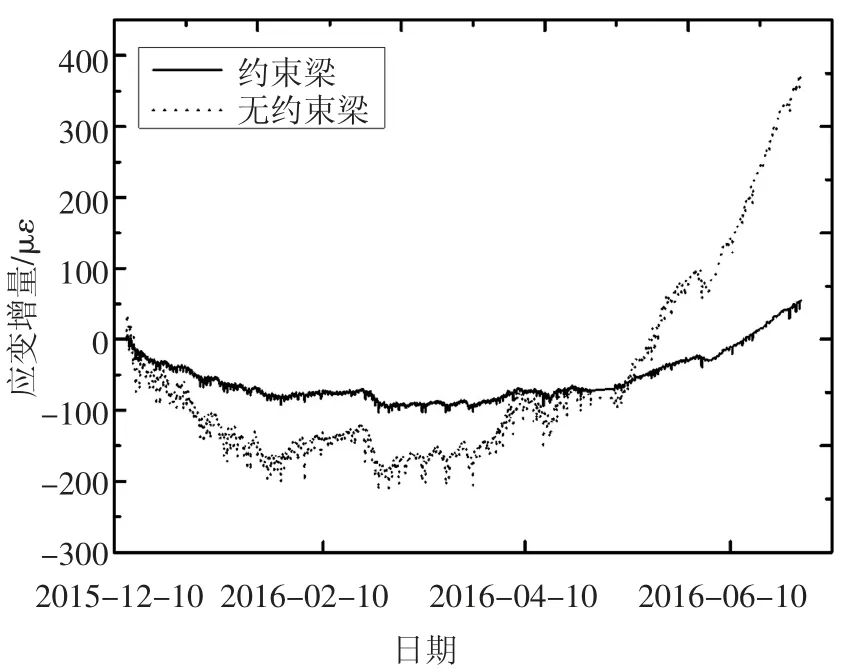
图15 空载段约束梁与无约束梁的应变增量对比Fig.15 Strain comparison for restrained and unrestrained beam in non-load stage

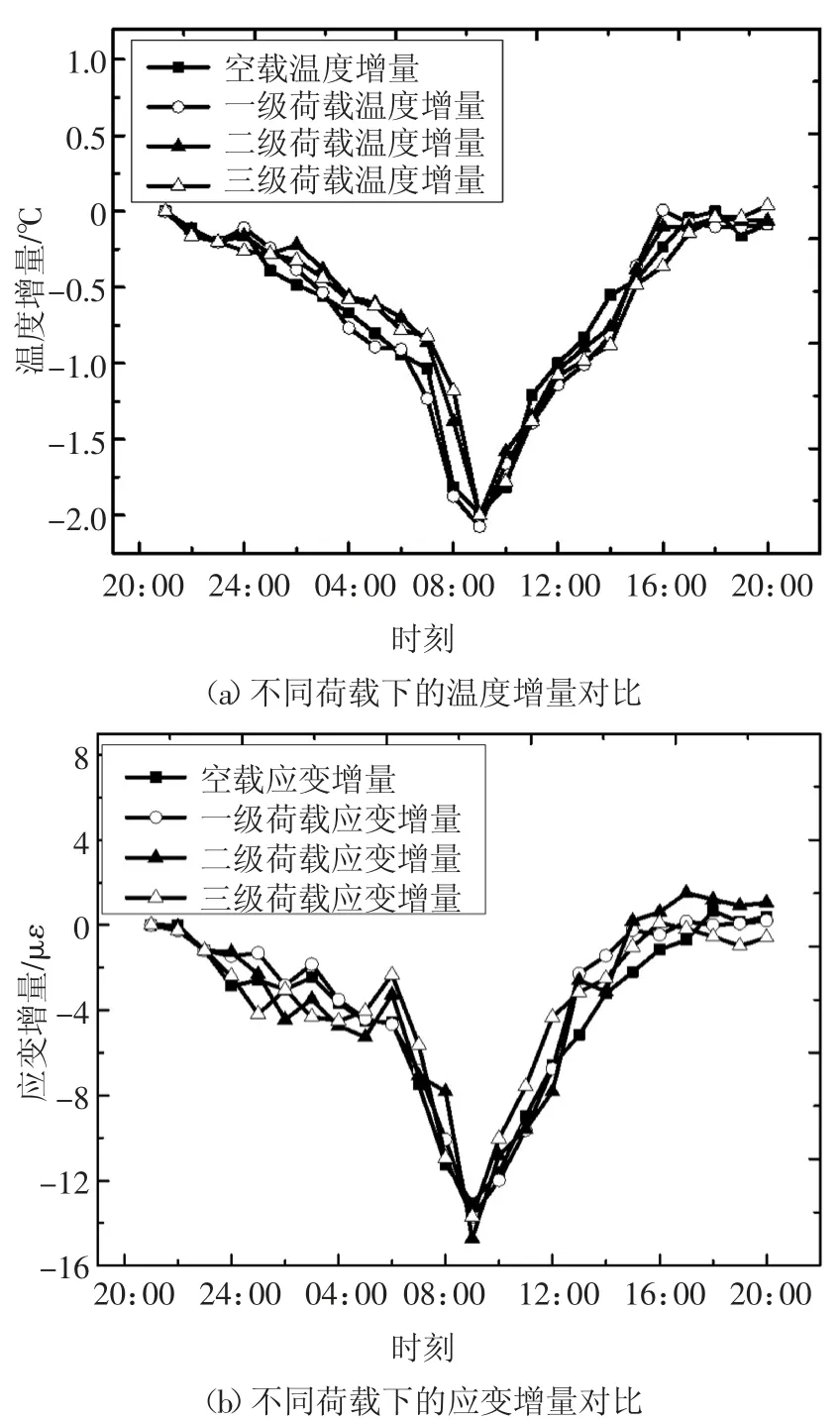
图16 无约束梁不同荷载下的数据对比Fig.16 Data comparison of unrestrained beam under different load

3.3 荷载作用下约束梁的应变分析

采用与无约束梁应变分析相同的方法，分析温度增量相同时，不同荷载对约束梁应变增量的影响.约束梁的温度增量和应变增量的曲线如图17 所示，由图17 可看出：当温度增量相同时，约束梁的应变增量随荷载增大而增大，上部荷载引起了约束梁的附加应变.将附加应变定义为相同温度下，约束梁有荷载时的应变增量与空载应变增量的差值.图18 所示为约束梁升温段和降温段三级荷载下的附加应变曲线.由图18 可看出，升温段和降温段的附加应变呈现相同的规律，当荷载恒定时，附加应变随温度的增大而增大；当温度恒定时，附加应变随荷载的增大而增大.

图17 约束梁不同荷载下的数据对比Fig.17 Data comparison of restrained beam under different load

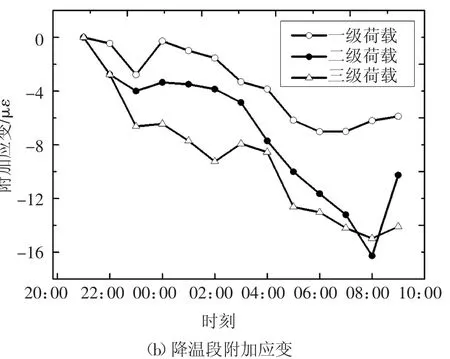
图18 约束梁不同荷载下的附加应变Fig.18 Extra strain of restrained beam under different load

3.4 附加应变的理论计算

在上部荷载及环境温度变化的作用下，约束梁的变形如图19 所示，梁会产生一定的挠度变形，附加应变由梁端反力对梁底部的二阶弯矩引起.

图19 约束梁在荷载下的变形图Fig.19 Deformation of the restrained beam under load

根据文献[17]，二阶弯矩在梁底部跨中引起的附加应变为：

式中：ΔM 为梁底附加弯矩；Pcr为梁的临界荷载[18].

根据第2 节所述的方法和图17 中的实测温度增量值，可计算出约束梁一个温度循环内每一时刻的弹性模量E 和转动刚度Kr，如图20 所示.由于每个荷载工况下的温度增量基本相同，因此可假定每个循环的弹性模量和转动刚度曲线一致.

将识别的参数代入式（10），可得出约束梁每级荷载下的附加应变计算值.为对比不同边界条件对附加应变的影响，分别计算了Kr=0、Kr=∞时的附加应变.图21 和图22 分别为降温段和升温段附加应变计算值和试验值的对比曲线.可看出，计算值与试验值的曲线趋势一致，降温段的一级荷载、二级荷载的计算值与试验值曲线吻合较好，其余曲线计算值与试验值有些差别.考虑到木材力学性能的离散性，且所有曲线计算值与试验值曲线均位于Kr=0和Kr=∞的计算值曲线之间，可以认为计算值与试验值之间的差异是可以接受的，附加应变的理论计算公式是合理的.

图20 约束梁加载时的弹性模量和转动刚度Fig.20 The modulus of elasticity and rotational stiffness of restrained beam under load

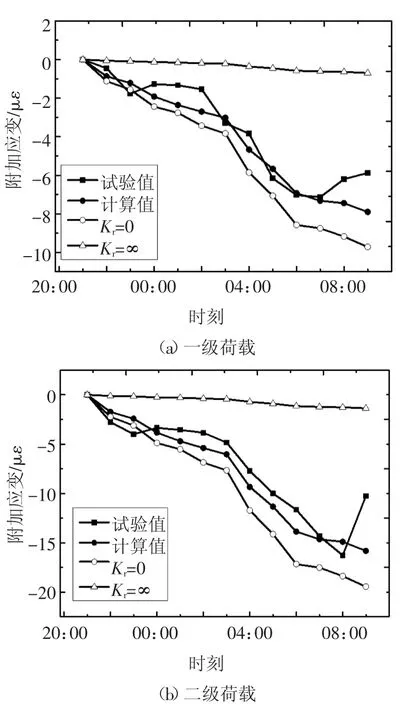
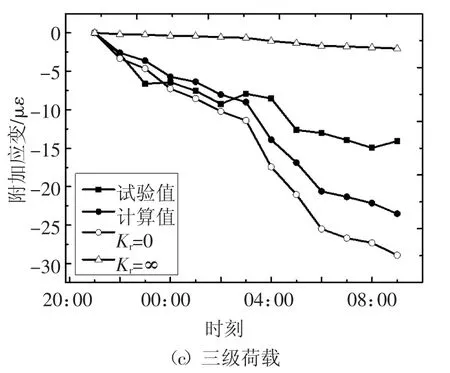
图21 降温段附加应变计算值和试验值对比Fig.21 Comparison between calculated and tested extra strain of temperature decreasing stage

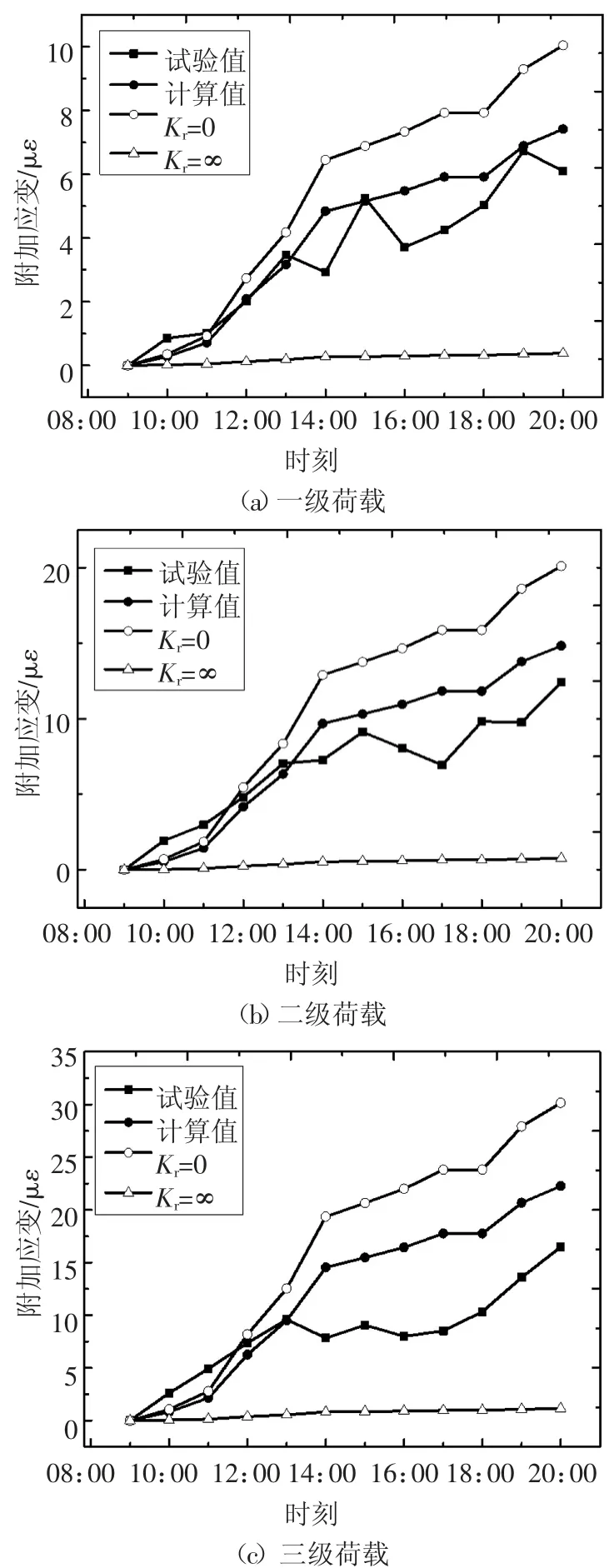
图22 升温段附加应变计算值和试验值对比Fig.22 Comparison between calculated and tested extra strain of temperature increasing stage

4 结 论

通过本文的分析，可得到以下结论：

1）通过无约束梁和燕尾榫约束梁的长期环境温度作用试验，可对其顺纹方向弹性模量、燕尾榫的拉压刚度、转动刚度等未知参数进行识别.考虑环境温度对木材材性的影响，将各未知参数识别成随环境温度变化的变量.

2）升温和降温时燕尾榫的受力状态不同，升温段的拉压刚度大于降温段.

3）上部荷载的变化对无约束梁在环境温度作用下的顺纹方向应变没有影响.

4）约束梁在环境温度作用下的顺纹方向应变随荷载增大而增大，上部荷载引起了约束梁的附加应变，且附加应变随荷载和环境温度的增大而增大.

5）根据附加应变的理论计算公式对附加应变进行了计算，计算值与试验值的对比说明计算公式是合理的.