非齐次马尔可夫跳跃正线性系统的稳定与镇定
2020-04-11蒋鹏飞奚宏生
蒋鹏飞,朱 进,奚宏生
(中国科学技术大学信息科学技术学院,安徽合肥 230027)
1 引言
现实中的许多系统,如经济系统[1]、生物系统[2]、功率分配系统[3]、排队过程[4]等,其状态、输出仅取非负值,此类系统称为正系统[5–6].随着正系统规模的日益复杂,系统结构会随着一些随机事件(如组件故障、子系统连接改变[7]等)的发生而变化,当此类随机事件的出现服从马尔可夫过程时,可以通过马尔可夫跳跃正线性系统(positive Markovian jump linear systems,PMJLSs)描述系统的动态特性.在研究PMJLSs稳定性时,鉴于子系统状态的正特性,很自然地会应用线性余正Lyapunov函数[8–11]来替代传统的二次型Lyapunov函数,它能充分利用系统自身的正特性进而使得稳定性分析更加简便.文献[9]通过设计切换线性余正Lyapunov函数得出平均稳定的充分判据.此后,文献[10]运用状态转移的方法分析了PMJLSs的稳定性并以线性矩阵不等式的形式给出随机稳定的充要判据.此后,PMJLSs中各种稳定性之间的关系得到研究,高阶矩稳定可得出低阶矩稳定,一阶指数稳定与平均指数稳定等价[11].基于稳定的判据,文献[12]分析了闭环PMJLSs的镇定问题并设计了状态反馈控制器,进一步地,带时延PMJLSs的L1随机稳定性和L1增益性能[13]得到了研究.
值得注意的是,PMJLSs的稳定及性能分析与马尔可夫过程的模态转移速率矩阵(mode transition rate matrix,MTRM)/模态转移概率矩阵(mode transition probability matrix,MTPM)密切相关,而以上关于PMJLSs的研究成果都是基于一个严格的假设:马尔可夫过程是齐次的,即MTRM/MTPM是定常的,但是这个假设在很多实际的系统中往往难以满足.一个典型的例子是功率分配系统[5],其中系统参数依赖于线性检测器、路径衰落等因素,其变化可通过PMJLSs进行建模,但由于工作环境会随时间而发生变化,从而PMJLSs中的MTRM/MTPM是时变的.同样的情况也存在于流行病学模型[5]中.因此,相较于现有的研究成果,非齐次PMJLSs能够更好地反映实际系统的特性,其研究也更具有一般性.文献[14]基于每个MTPM对应的PMJLS都是稳定的这一假设,采用平均逗留时间方法给出了系统稳定的充分条件,然而该稳定判据约束太强,不具备普遍性.因此非齐次PMJLSs的稳定与镇定问题仍需要进一步的研究与探索.
本文研究一类非齐次PMJLSs的稳定与镇定问题,其中MTRM/MTPM在一段时间内保持不变或变化甚微,但在整个时间区间上却是随机变化的,且该变化可以通过马尔可夫过程加以描述.文中提出一种双层PMJLSs模型来描述MTRM/MTPM的时变性,其中低层马尔可夫过程表示系统模态的变化,高层马尔可夫过程表征低层马尔可夫过程MTRM/MTPM的随机变化.基于此模型,通过设计切换线性余正Lyapunov函数,分别推导出连续和离散时间非齐次PMJLSs平均稳定的条件.其次,为非齐次PMJLSs设计了依赖于模态–MTRM/MTPM的状态反馈控制器,并通过线性规划方法求解控制增益.相较于传统依赖于模态的控制器设计,本文提出的状态反馈控制器更具一般性;最后,以功率分配系统为例给出仿真实例,验证所提控制策略的有效性.
2 系统描述
考虑下面连续和离散时间非齐次马尔可夫跳跃线性系统:
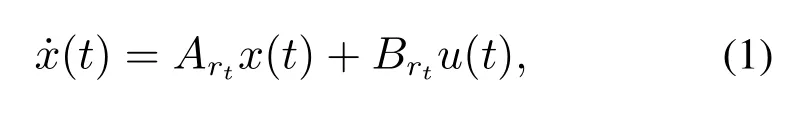
和
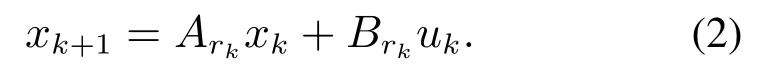
对连续时间系统(1),x(t)是系统状态向量,为输入向量,是Metzler矩阵,≽0.{rt ∈N={1,2,···,N},t0}是表示系统模态跳跃的低层马尔可夫过程,其MTRM可表示为
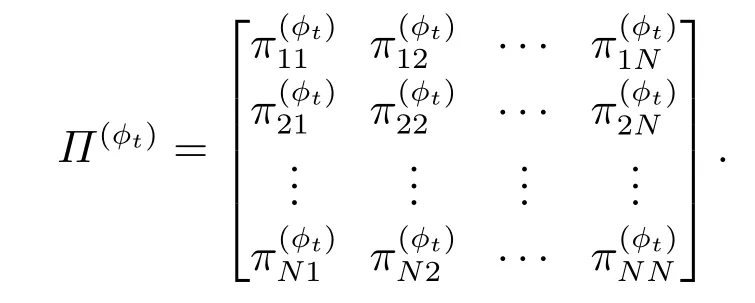
相应地,模态转移概率可定义为
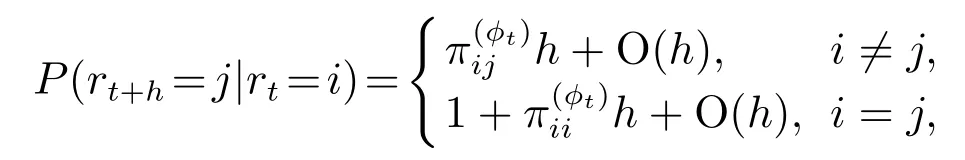
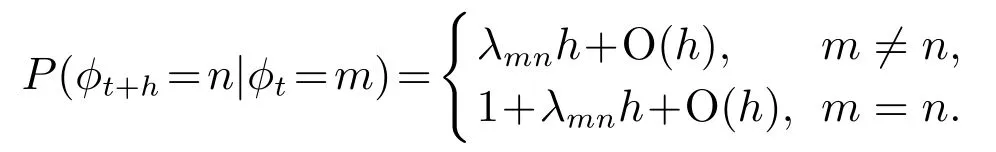
对离散时间非齐次马尔可夫跳跃系统(2),系统矩阵满足Ark ≽0,Brk ≽0.{rk,k0}是在状态空间N上取值的马尔可夫链,并且其模态转移概率满足而{ϕk,k0}是一个用来表征MTPM切换的高层马尔可夫链,高层模态转移概率矩阵(HMTPM)表示为Q=[qmn]M×M.
定义1[4]对式(1)–(2)所描述的马尔可夫跳跃线性系统,若对任意的初始状态x(0)≽0和r0∈N,ϕ0∈M,始终有x(t)≽0(xk ≽0),则对应的系统为马尔可夫跳跃正线性系统(PMJLSs).
定义2[4]对任意初始状态x(0)≽0和初始高低层模态r0∈N,ϕ0∈M,若系统的状态变量满足以下条件则称系统(1)或系统(2)是平均稳定的.
由系统描述中可知,所建立的非齐次跳跃系统模型具有双层马尔可夫切换,以离散时间系统(2)为例说明:系统模态的变化由一个低层的Markov链控制,而模态之间的切换概率取决于MTPM.由于各种随机因素的影响,系统模态之间的转移概率是时变的,即MTPM是时变的.当MTPM在有限状态空间M={MTPM 1,MTPM 2,···,MTPMM}上随机切换时,则低层Markov链的模态切换如图1上图所示.此外,MTPM的随机变化受一个高层Markov链驱动,把每个MTPM定义为一个高层“模态”,则高层模态在HMTPM控制下的转移如图1下图所示.简而言之,此类双层切换就是用一个高层Markov链来表示低层Markov链的MTPM的随机变化特性,即用一个高层的Markov链来表征系统的非齐次特性.
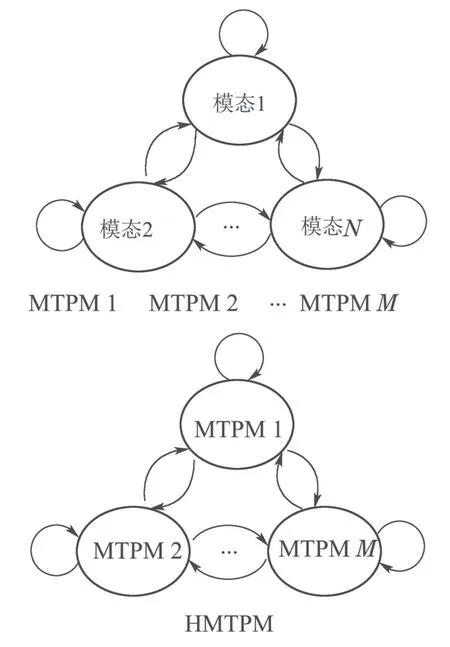
图1 低层模态和高层模态切换示意图Fig.1 The switching of low-layer system mode and high-layer mode
3 连续时间PMJLSs的镇定问题
3.1 稳定性分析
引理1[12]任意矩阵A ∈Rn×n是Metzler矩阵的充要条件:存在一个常数ξ >0,使得A+ξIn ≽0.
引理2[15]连续时间马尔可夫跳跃线性系统(1)(u(t)=0)是PMJLSs的充要条件:对任意i∈N,Ai是Metzler矩阵.
定理1对任意的i ∈N,m ∈M,若存在一组向量使得下式成立:
则u(t)=0的连续时间非齐次马尔可夫跳跃线性系统是平均稳定的.
证因为Ai是Metzler矩阵,根据引理2 可知u(t)=0的系统(1)是PMJLSs.考虑到正系统中状态变量的正特性,引入切换线性余正Lyapunov函数:
结合条件(3),显然有V(xt,i,m)>0.在t,x(t)=xt,rt=i,ϕt=m处马尔可夫过程的无穷小算子:
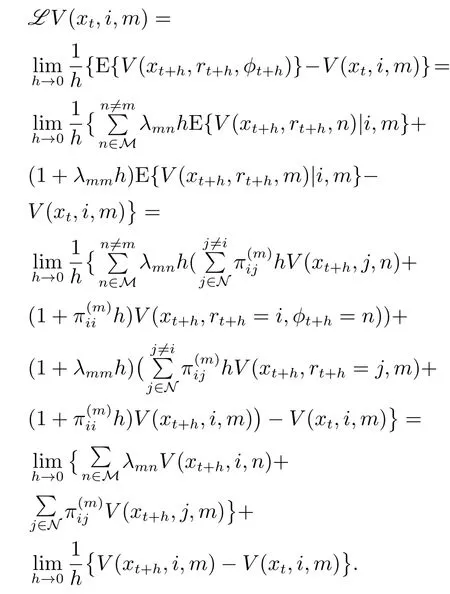
当h→0时,xt+h→xt,可进一步得出
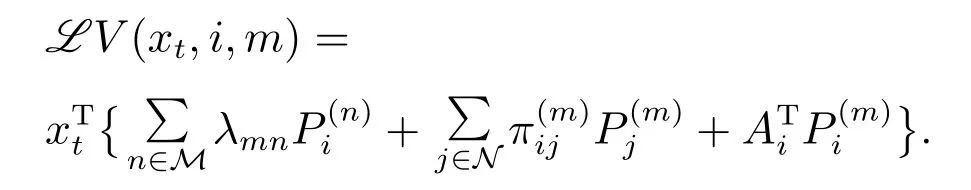
因为x(t)≽0始终成立,由定理1条件(4)可得出L V(xt,i,m)<0,所以系统是一阶稳定的.而在证系统一阶稳定与平均稳定等价. 证毕.
3.2 控制器设计
对非齐次PMJLSs而言,在设计控制器时不仅要考虑闭环系统的稳定性同时还要保证正特性.另外,考虑到MTRM的时变特性,设计具有以下形式的状态反馈控制器:
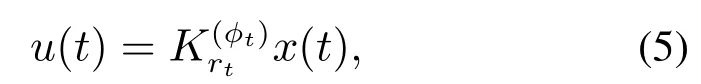
定理2考虑连续时间非齐次马尔可夫跳跃正线性系统(1),对任意的i ∈N,m ∈M以及任意给定的m维向量若存在常数以及两组向量使得下式成立:
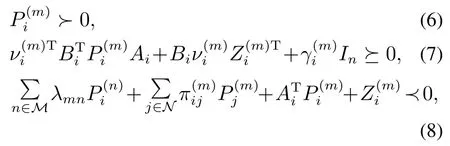
则经由下述模态–—MTRM相关的状态反馈控制器
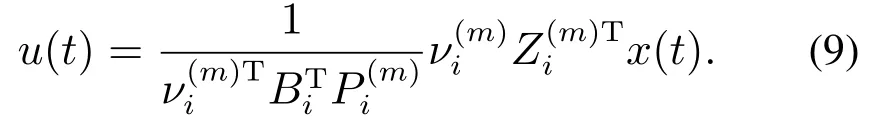
闭环系统能够实现平均稳定性,同时保持系统的正特性.
证首先证明经由反馈控制u(t)后的闭环系统仍是正系统.对任意的i∈N,m∈M有因此始终是正标量.对式(7)两边同时乘以得
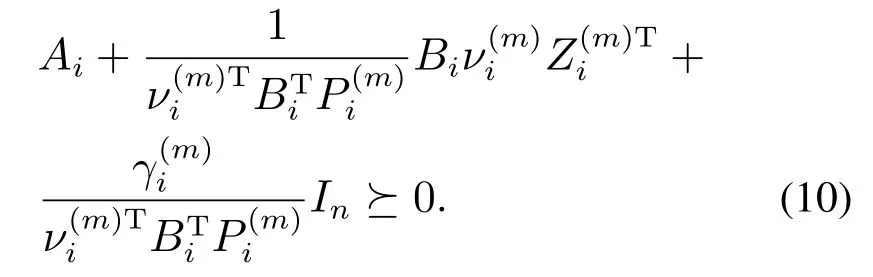
联立式(9)–(10),得
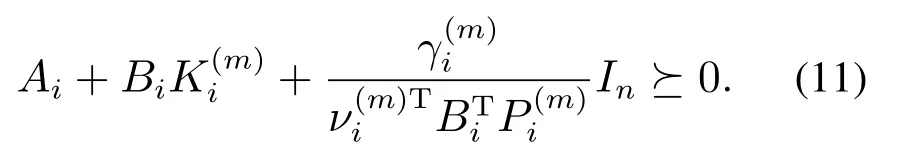
接下来,证明闭环系统的平均稳定性.联立式(1)(5)可得闭环系统,
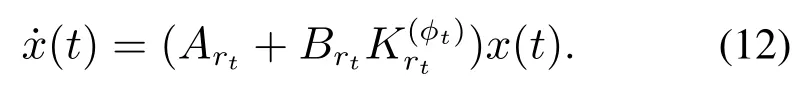
由定理1可知,闭环系统平均稳定的条件是
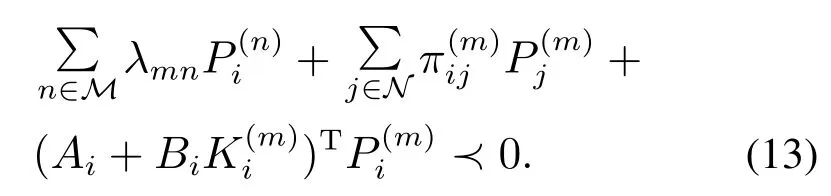
结合式(9),可以得出
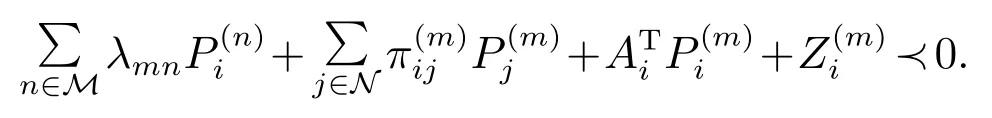
证毕.
注1若Π(ϕ)≡Π,则非齐次马尔可夫跳跃正系统(1)退化为齐次马尔可夫跳跃正系统.相应地,依据定理1和定理2可得出有关齐次马尔可夫跳跃正线性系统平均稳定的结论,该结论已在文献[12]中导出.由此可见,本文的结论更具一般性,可视为齐次正系统稳定判据的扩展与补充.
4 离散时间PMJLSs的镇定问题
4.1 稳定性分析
引理3[15]离散时间马尔可夫跳跃线性系统(2)(uk=0)是PMJLSs的充要条件:对任意i∈N,Ai ≽0.
定理3对任意的i ∈N,m ∈M,若存在一系列向量使得下列式子成立:
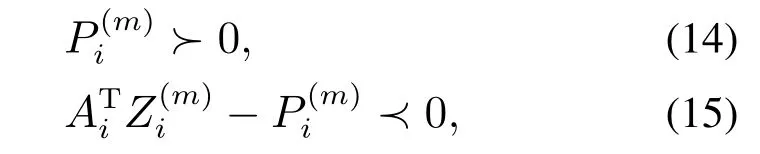
证首先设计切换余正李雅普诺夫函数

在xk,rk=i,ϕk=m处的Lyapunov差分为
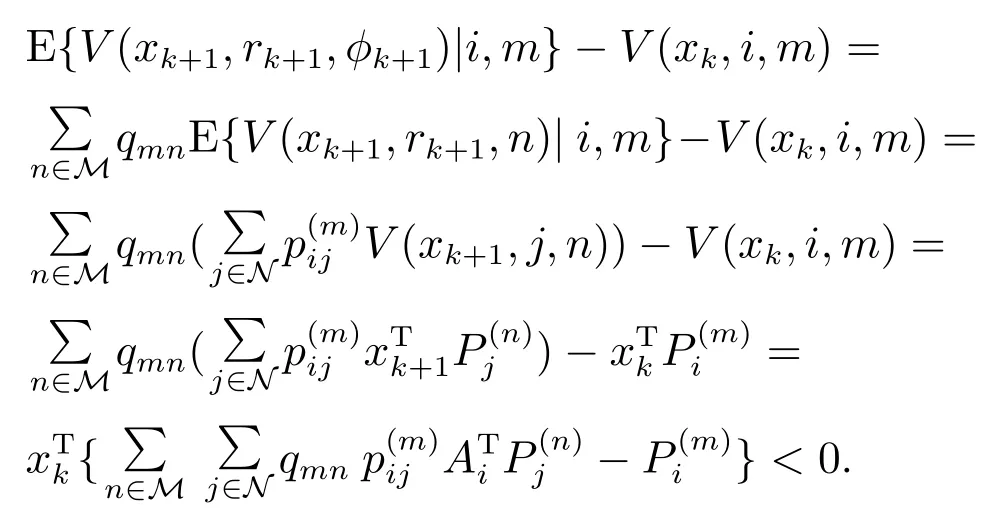
结合Lyapunov函数的稳定判据可知,u(k)=0的系统(2)是平均稳定的. 证毕.
4.2 控制器设计
下面考虑离散时间系统的镇定问题,考虑具有以下形式的状态反馈控制器:
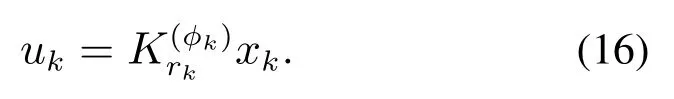
定理4考虑离散时间非齐次马尔可夫跳跃正系统(2),对任意i ∈N,m ∈M以及任意一个给定的正向量若存在两组向量使得下列式子成立:
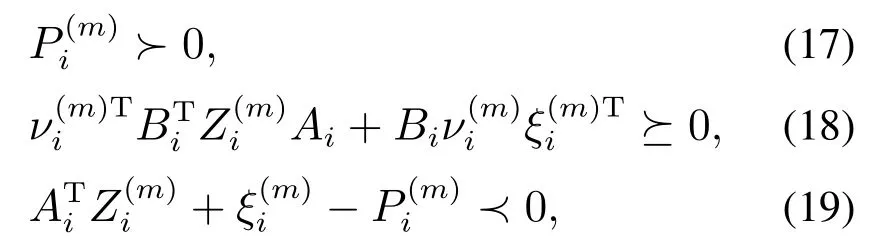
则通过下述给出的模态—–MTPM相关的状态反馈控制器:
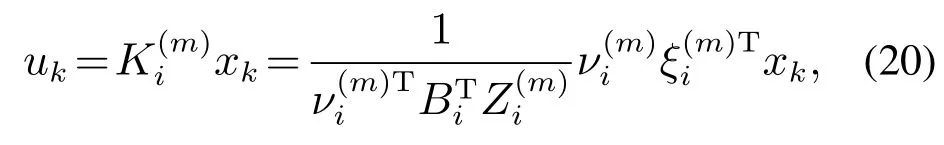
闭环系统能够达到平均稳定,并且保持正特性,式中:
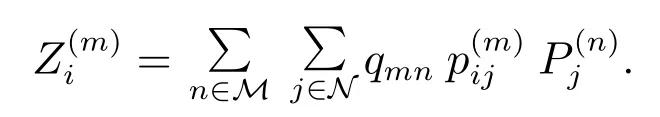
证首先证明闭环系统是正系统.对任意i,m,Bi始终是正标量,由式(18)得
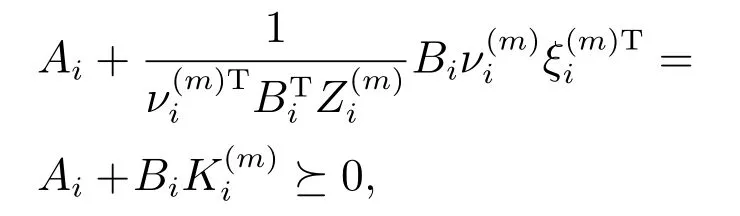
所以闭环系统(2)是正系统.
与定理2的证明类似,可得出具有控制器uk的闭环离散时间非齐次跳跃正系统(2)是平均稳定的.
证毕.
注2通常来说,模态—–MTPM相关的反馈控制器对具有时变MTPM的非齐次马尔可夫跳跃正系统有很好的控制效果,与传统的模态相关的控制器相比,此类控制器的保守性更低.
5 数值仿真
本节将给出两个数值实例,然后对其进行稳定性分析并设计控制器来验证所提方法的有效性.
5.1 连续时间非齐次跳跃正系统
考虑文献[3]中建模为PMJLSs 的功率分配系统,系统状态方程描述为
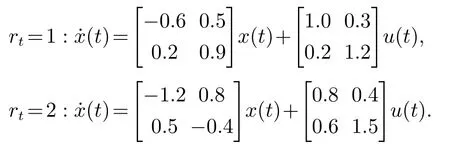
系统的MTRM是时变的并且取决于系统的工作环境,为了便于描述,把工作环境分为两类:ϕt=1表示环境“优”、ϕt=2表示环境“良”,这两种环境对应的MTRM分别为Π(1),Π(2):
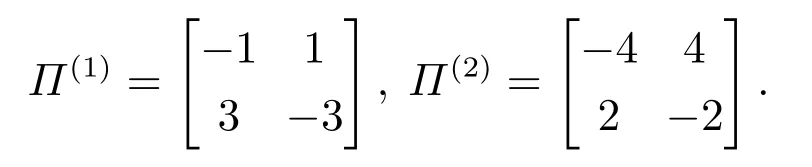
定义系统运行环境的变化服从一个高层Markov过程,其高层模态转移速率矩阵为
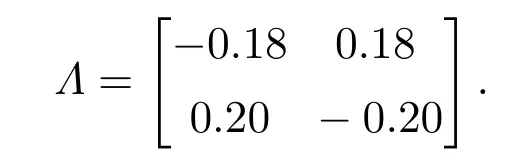
根据低层Markov过程MTRM可以计算出系统模态的平稳分布,其概率关系如下:MTRM为Π(1)时,πrt=1=3×πrt=2.MTRM为Π(2)时,πrt=1=0.5×πrt=2.上述理论分析说明:当环境为“优”时(ϕt=1),系统处于模态rt=1的概率更大,当环境为“良”时(ϕt=2),系统处于模态rt=2的概率更大.
图2给出了100 s内系统MTRM变化和模态变化的一个样本实现.高层模态的变化模拟了实际系统运行环境的变化情况,也就是“优”、“良”环境在整个时间段上的随机变化情况;低层模态的变化轨迹模拟了实际系统在子系统1和子系统2之间的切换情况.从图2可以直观地看出在时间段t ∈{[0,8],[18,45],[60,70]}上,高层模态MTRM都是ϕt=1,在此时间段上低层模态停留在rt=1的时间更长,这就对应了当处于“优”的环境,系统处于子系统1的概率更大.在时间段t ∈{[10,15],[48,58],[72,88]}上,高层模态MTRM都是ϕt=2,在此时间段上低层模态停留在模态rt=2的时间更长,这就对应了当处于“良”的环境,系统处于子系统2的概率更大.系统在各个低层模态的逗留时间体现了在不同MTRM作用下,系统在子系统1和子系统2之间的切换情况,也就说明了高层模态对低层模态切换的影响.为了更为精确地表现出不同高层模态作用下各低层模态的切换情况,本文随机生成50组高低层模态的跳跃样本,表1统计了这50组样本中不同MTRM作用下各低层模态的逗留时间.

图2 高层模态MTRM(ϕt)和低层模态(rt)切换的一个样本Fig.2 A sample of high-layer mode ϕt and low-layer mode rt

表1 不同MTRM作用下低层模态的逗留时间(s)Table 1 Residence time of low-level modes under different MTRM(s)
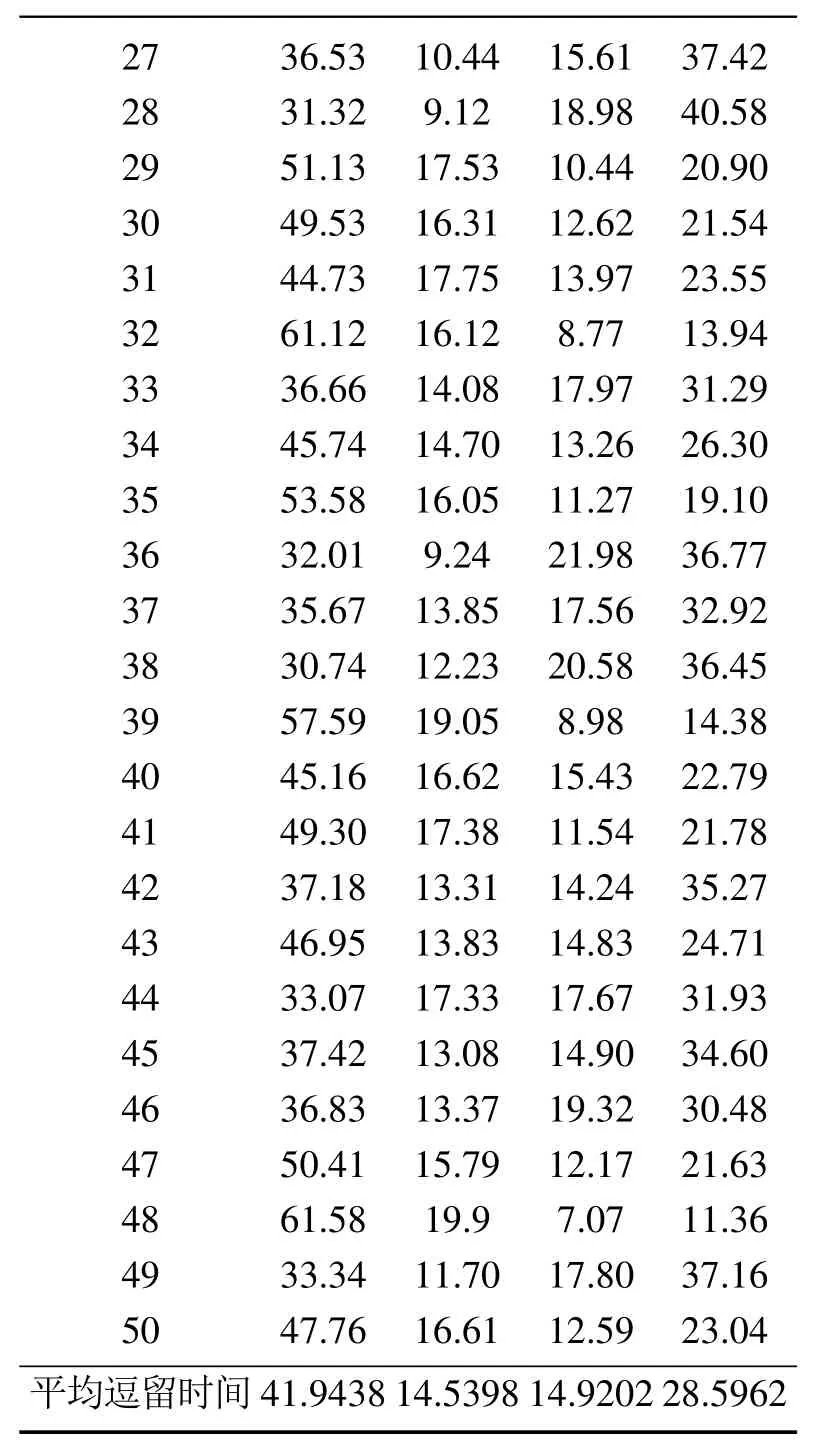
由表1统计可知,在100 s的运行时间上,当处于高层模态MTRM1时,两个低层模态平均逗留时间的比值为

当处于高层模态MTRM2时,两个低层模态平均逗留时间的比值为
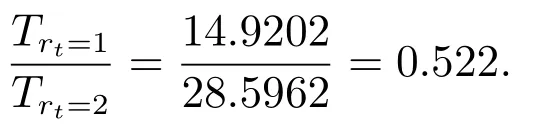
根据以上分析,双层模态的切换图直观地反映了系统各个模态的逗留时间;而在同一个高层模态下,低层模态平均逗留时间的比值能够反映出系统的平稳分布情况,并且反映的结果与理论分析一致.综合可以得出高层模态的取值直接影响着低层模态的切换情况,由此可体现出高低层模态切换的关系.
初始条件为x(0)=[0 0.1]T,rt=1,ϕt=1时,开环系统状态轨迹如图3(a)所示,可以看出在无控制输入时,系统不稳定.下面考虑对系统施加控制,根据定理2,选取然后利用MATLAB中的线性规划工具箱可求解出可行解:


对闭环PMJSLs,给定初始状态[300 200]T,然后根据当前子系统rt和环境ϕt施加对应的控制量,可得闭环系统的状态轨迹如图3(b)所示.从图可出系统的状态最终收敛到平衡点,所以经由模态–—MTRM依赖的状态反馈控制器闭环系统实现了平均稳定性,进而验证了本文所提出的控制策略的有效性.

图3 连续时间开环和闭环PMJLSs状态轨迹Fig.3 State trajectory of continuous-time open-loop and closed-loop PMJLSs
5.2 离散时间非齐次跳跃正系统
考虑两模态的离散时间非齐次PMJLSs,其方程描述为
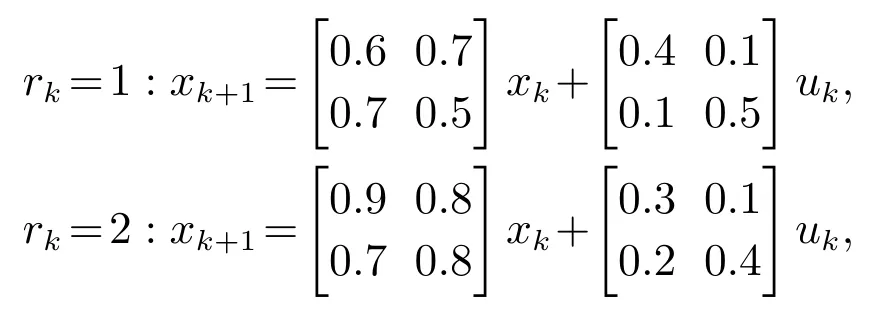
其中MTPM在有限集M={1,2}中取值,MTPM的切换由高层模态转移概率矩阵Q描述.
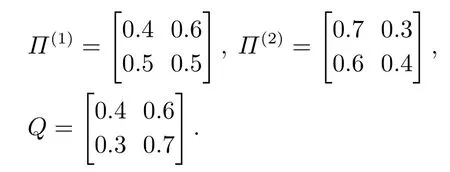
文献[14]判断一个非齐次PMJLS系统稳定的前提是所有的子系统稳定,由系统矩阵可知子系统不稳定,所以文献[14]的结论无法对此类系统进行稳定性分析.而通过本文定理4却可以设计出使得系统稳定的控制器.选取可得模态MTPM依赖的状态反馈控制器.

当初始状态为[300 200]T时,离散时间闭环系统的状态轨迹如图4所示:随着时间的演化,闭环系统的状态趋于平衡点.所以经由所设计的控制器系统实现了平均稳定性.这种控制器的设计对子系统是否稳定没有限制,所得出的结论更具一般性.
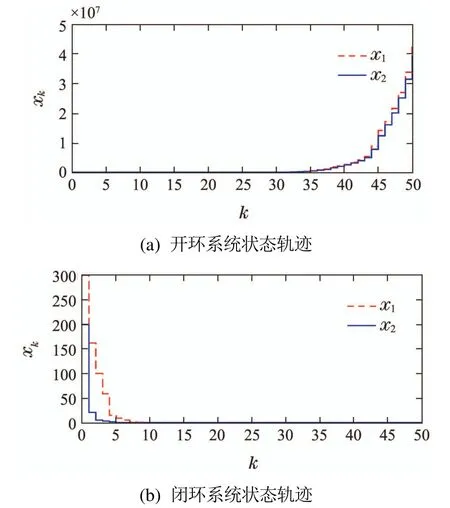
图4 离散时间开环和闭环PMJLSs状态轨迹Fig.4 State trajectory of discrete-time open-loop and closedloop PMJLSs
6 总结
本文研究了一类非齐次马尔可夫跳跃正系统的稳定与镇定问题,其中系统模态及模态转移速率/概率矩阵的随机切换均可通过马尔可夫过程进行描述.通过设计切换线性余正李雅普诺夫函数,给出系统平均稳定的充分判据,并设计依赖于模态MTRM/MTPM的状态反馈控制器实现系统稳定.鉴于现有的齐次马尔可夫跳跃正系统可作为本文所提模型的一个特例,文中给出的稳定性判据和控制器设计方案更具一般性.
