抗扰控制中的不变性原理
2020-04-11李向阳高志强
李向阳,高志强
(1.自主系统与网络控制教育部重点实验室;华南理工大学自动化科学与工程学院,广东广州 510640;2.克里夫兰州立大学电气工程与计算机科学系,俄亥俄克里夫兰44115,美国)
1 引言
自动控制系统的设计目标是使被控系统的运动状态和系统的工程实现达到人们所期望的稳定性、快速性、准确性和经济性等指标要求.由于被控系统的建模误差和外部扰动等不确定性普遍存在,简单的开环控制往往不能满足人们对控制性能的期望,闭环反馈控制成为自动控制的基本方法.随着控制理论研究的输入,新型控制算法不断被提出,但是实际工程中PID仍然占90%[1].不过,近年来随着抗扰控制理论的逐步完善和抗扰控制算法的实际应用效果被工业界所认可,特别是自抗扰控制(active disturbance rejection control,ADRC)被TI等多家公司固化到其数字信号处理器(digital signal processor,DSP)芯片和控制软件中[2],情况有所改变,ADRC正在成为既PID之后另一种广泛应用的通用控制策略,在一些对控制性能要求较高的场合,ADRC有替代PID的趋势.因此,探索抗扰控制的运行机理和不同抗扰控制方法之间的关系是非常必要的.
一般控制系统结构如图1所示,它是许多控制系统分析和综合的基本框图.图1中:Gp是被控系统;Gc是控制器;r,y,u和ξ分别是设定值、系统输出、控制器输出和外部扰动;e是设定值和系统输出值之间的误差、是控制器的输入,控制器根据e来产生u;控制的目标是在外部扰动作用下仍然能保持该误差在要求范围内.
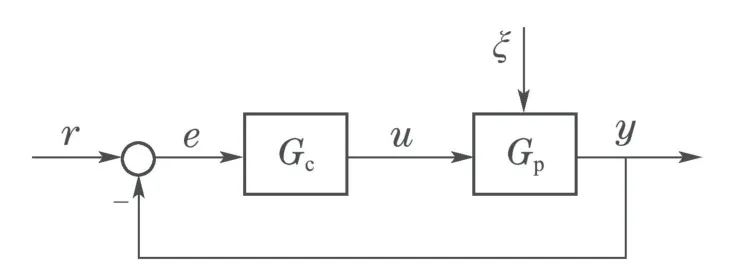
图1 一般控制系统结构Fig.1 Structure of the general control systems
图1的一般控制系统只有一个控制器Gc可以调节,是一自由度(one-degree of freedom,1–DOF)的误差纠正控制系统,1–DOF控制很难同时实现设定值跟踪、保持被控对象在外部扰动、内部结构和参数变化后系统输出的不变性,往往需要在不同控制性能指标之间寻找平衡,使得控制器参数的整定非常困难.PID控制算法虽然简单通用,但是在PID控制器在投入实际工程中运行前,参数整定是一件非常费时费力的事情,而且随着系统参数的变化或者工况的改变,控制性能将变差,甚至出现不稳定现象,更不用说实现优化控制了.此时,往往需要重新再次整定PID控制器参数,这个过程一直伴随着控制系统的整个生命周期.于是,自适应控制、鲁棒控制、变结构控制等各种控制方法被提出和不断改进,这些方法从不同的角度来处理控制系统的不确定性,成为控制理论研究的重要领域,在一些能够获得被控对象的较精确模型的特定领域得到了应用,它们丰富的理论成果对控制理论的其它方法也有启发和借鉴作用.本文从抗扰的角度研究典型抗扰控制方法的内在联系及其它们所遵循的不变性原理,针对双通道扰动补偿控制、内模控制(internal model control,IMC)、基于扰动观测器的控制(disturbance observer-based control,DOBC)和ADRC的结构所实现自由度及其每个自由度的功能,阐明不变性原理的不同表现形式,以便更好地理解和应用抗扰控制方法,也为进一步更好地发展抗扰控制方法提供参考.
论文剩余部分安排如下:第2节陈述了双通道扰动补偿控制中的不变性原理,该扰动补偿原理要求扰动可测量,后续章节研究了当扰动不测量时的抗扰方法;第3 节研究了1–DOF 和二自由度(two-degree of freedom,2–DOF)内模控制结构和抗扰原理,内模控制实现了名义模型的不变性;第4节研究了线性DOBC的2–DOF的结构和抗扰机制,DOBC通过扰动的估计和补偿实现名义模型的不变性;第5节分析了ADRC的三自由度(three-degree of freedom,3–DOF)结构,在陈述实现线性系统和非线性系统统一表示的积分器串联模型的基础上,介绍了3–DOF中每个自由度的具体算法,分析了ADRC中实现的标准积分串联模型和准滑动模控制的两种不变性原理的实现机制;最后,论文在第6节对全文进行了总结.
2 双通道扰动补偿控制
图1中的控制器Gc要同时克服外部扰动ξ跟踪变化的参考信号r,这样的控制器比较难以获得较高的控制性能.但是,可以实时测量外部干扰ξ时,可按照图2来设计一个补偿控制器Gηξ,使其输出η作用于被控对象Gp后对系统输出y的影响与外部干扰ξ对系统输出y的影响正好相反,考虑图2中的符号,即有
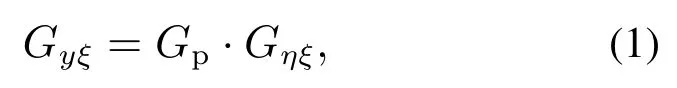
式中Gyξ是外部干扰ξ到系统输出y的传递函数.
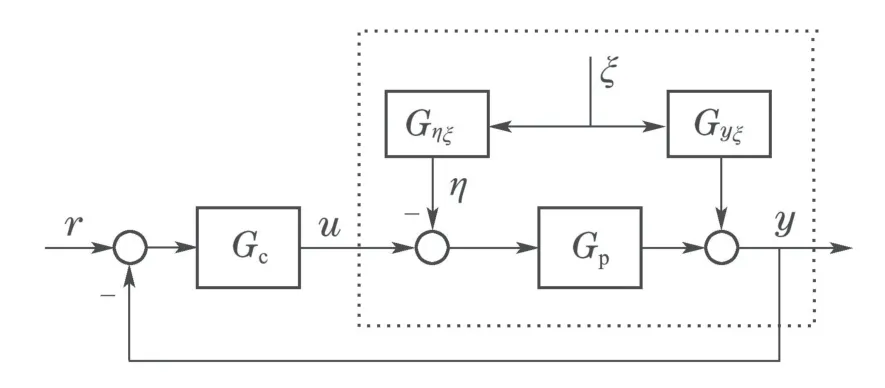
图2 双通道扰动补偿控制Fig.2 Dual-channel disturbance compensation control
当式(1)成立时,从u到输出y的传递函数Gyu为
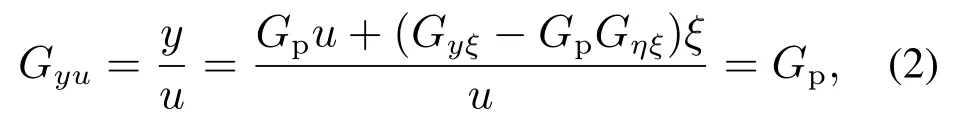
即Gyu与外扰ξ无关,实现了外扰对系统输出的不变性.图2通过建立一个新的扰动通道来产生η并在系统输入中进行补偿,补偿量的大小和相位与原来外扰对系统输出的通道相同,使外扰ξ经过双通道在系统输出的影响相互抵消,双通道扰动补偿控制原理又称绝对不变性原理,前苏联者学者G.V.Schipanov在1939年提出,并经J.Preminger进一步发展使其在1960年后得到广泛接受和大量应用[3],其实,从技术实现的角度来看,中国古代指南车的运行机制就蕴含不变性原理[4].
图2中存在主控制器Gc和补偿控制器Gηξ两个控制器,是一个2–DOF控制系统,参数整定可以分开进行.补偿控制实现抗外扰;设定值跟随和抗击被控对象Gp参数变化的内扰仍然由主控制器同时完成.在实现方面,双通道扰动补偿控制要求扰动可测量,需要安装相应的传感器,有时在实际工程中难以实现.内模控制通过引入模型误差反馈来实现不变性原理,达到抗扰的目的,内模控制方法不要求扰动可测量.
3 内模控制
内模控制理论作为控制系统设计方法一般方法在1980年左右形成[5–6].图3是内模控制的系统结构图,Gn是被控对象的标称模型,GIMC是内模控制器,d是等效到被控系统输入侧的外部扰动.为陈述内模控制的基本原理,假设Gp是最小相位系统,则GIMC一般采用式(3)的取法,式中,Q为适当阶次的低通滤波器,满足式(4),GIMC依赖于Gn,Q的阶次一般取比GIMC至少高一阶,以保证内模控制器GIMC可物理实现,内模控制是基于模型的.

注1本文中的符号表示中,没有特别说明时,可以理解为频域表示或者时域表示.
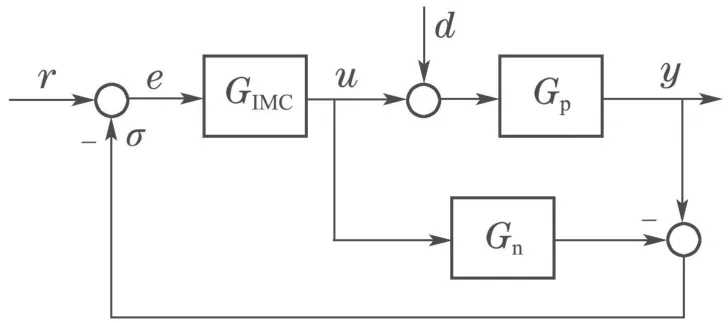
图3 内模控制系统结构Fig.3 Structure of internal mode control system
由图3,有

从式(6)可以看出,σ是由模型误差(Gp−Gn)和外部等效扰动d产生的.把式(3)代入式(5)有
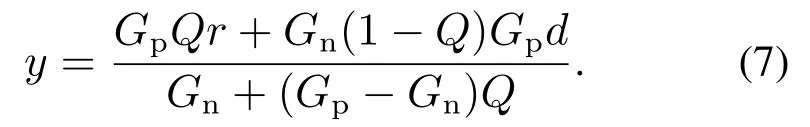
由式(4)有

当Gn=Gp时,有
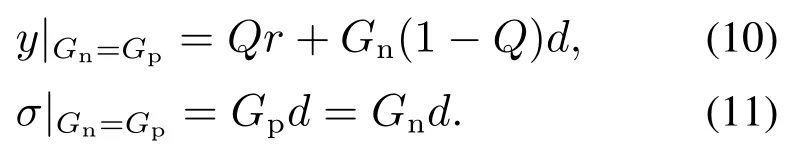
从式(8)可知,内模控制实现了对设定值的跟踪;从式(9)可知,σ是模型误差(Gp−Gn)和外部等效扰动d引起系统输出的综合误差,该误差还与设定值有关.为了实现对设定值跟踪问题和扰动估计的分离,把图3的GIMC向前移出相加点,并分别用Gff和Gfb代替,如图4所示.当GIMC=Gff=Gfb时,图4与图3等价;当Gff和Gfb可以独立调节时,图4为2–DOF内模控制系统,是对图3的内模控制系统的改进.
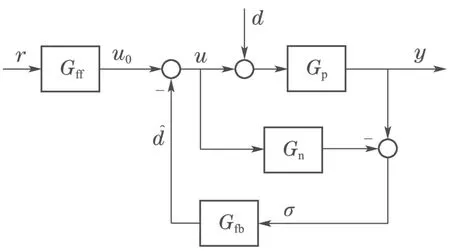
图4 2–DOF内模控制系统结构Fig.4 Structure of 2–DOF IMC system
图4的2–DOF内模控制中,Gff和Gfb分别用于设定值跟踪和抗扰.按照与式(3)同样的设计有

于是有
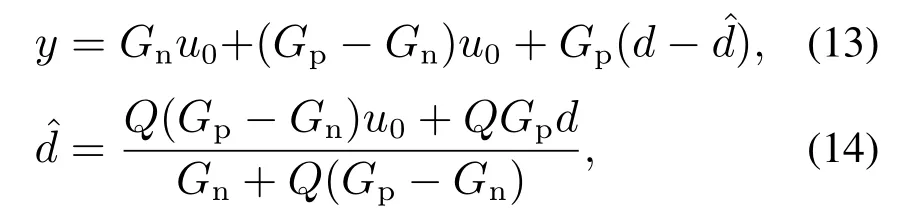
因此有
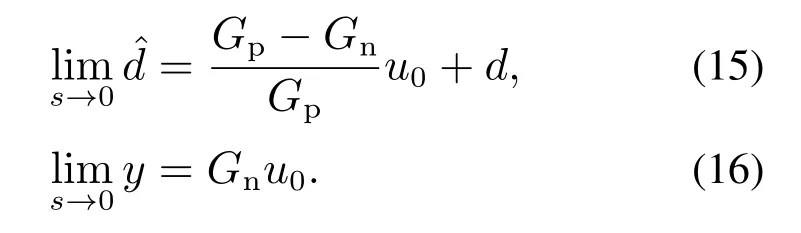

式(17)的Qr可选择不同于Q低通滤波器,以便满足一定控制性能指标要求,但同样有

由式(13)–(14)和式(17)有
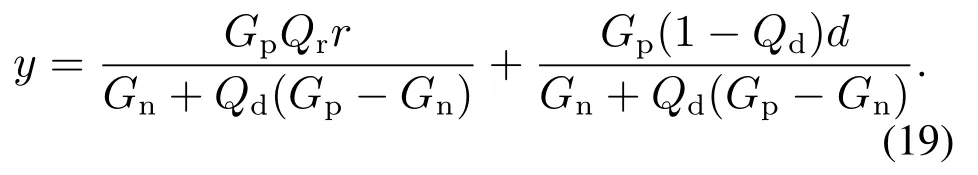
从式(7)和式(19)对比可以看出,采用2–DOF内模控制可以实现抗扰和设定值跟踪分别由两个不同的滤波器Qd和Qr来完成,实现了设定值跟踪控制和扰动补偿控制的解耦,简化了参数调整.
4 基于扰动观测器的控制
当图4的模型误差和外部扰动较大时,或者对控制性能要求较高时,采用前馈控制器Gff很难达到性能指标要求.把图4的Gfb等价地移到相加点之前,并用代替,为了进一步提高控制系统性能,把前馈控制Gff改为反馈控制Gc而得到图5的线性DOBC系统.
由于图5中虚线框具有扰动估计能力,因此叫扰动观测器[7],整个2–DOF控制系统叫DOBC.一般情况下,标称模型Gn与实际对象模型Gp是有误差的,设
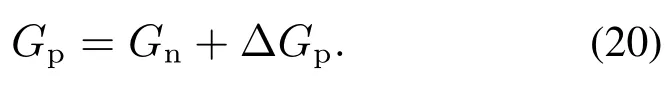
把式(20)代入式(14)和式(13)有
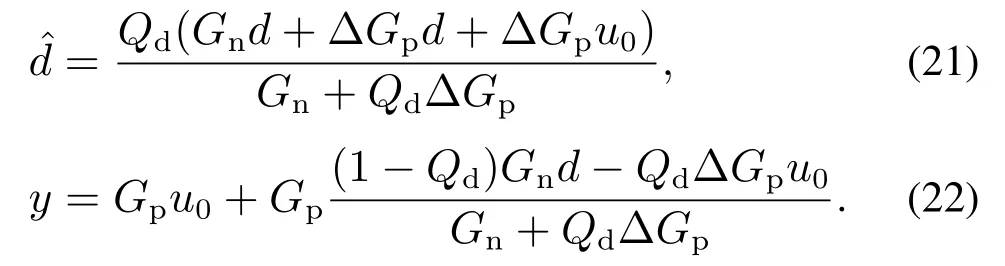
当Qd的带宽比d和∆Gp大四倍以上时,有
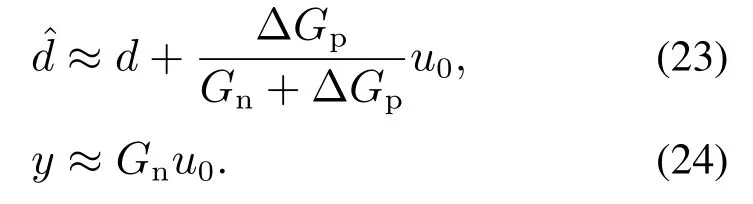
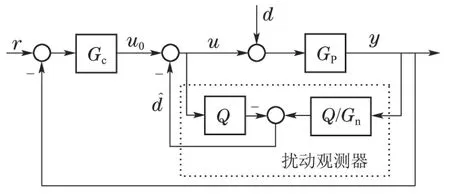
图5 二自由度的线性DOBCFig.5 Linear DOBC with 2–DOF
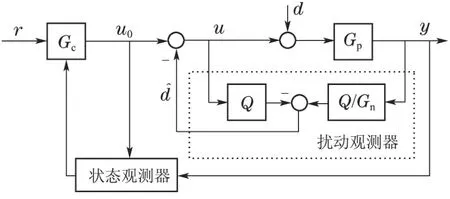
图6 带状态观测器的线性DOBC系统结构图Fig.6 Structure diagram of linear DOBC system with state observer
5 自抗扰控制
ADRC是中国科学院韩京清先生在1998年系统地提出来的、能同时处理线性和非线性系统的一套完整的理论[9–10],经过20来年的发展,ADRC在理论方面得到了一定假设条件下的证明,在应用方面飞速发展,成为控制工程中重要的通用控制范式和算法.韩京清先生反思现代控制理论的现状,认为尽管其理论非常完善,但由于其控制方法的有效性过于依赖于被控对象的精确模型,以致其适应性不强和可移植性差,因而很难在实际工业中大量应用;相反,由于经典PID控制器采用基于误差来消除误差的原理,其对被控对象的模型精度要求不高,而得到广泛应用.ADRC不仅吸收了PID控制的优点,而且韩京清先生在研究线性和非线性被控对象的输入输出模型关系后,指出在一定条件下,线性系统和非线性系统可以统一采用积分器串联模型来表示,俗称韩式标准型.该标准型中未知非线性部分为时变信号,并只在最高次方程中出现,ADRC 用韩式标准型这种时变局部模型代替以往控制系统(包括前述的IMC和DOBC)设计中所采用的系统全局模型,这为ADRC可以同时解决线性系统和非线性系统的控制问题以及吸收现代控制理论中的观测器研究成果提供了基础[11–12];此外韩京清先生还创新地提出了ESO[8]、跟踪微分器(tracking differentiator,TD)[13]和非线性状态误差反馈控制律(nonlinear state error feedback,NLSEF)[14]的思想和具体算法,最终形成了完整的理论体系[15–18].ADRC把图6带状态观测器的线性DOBC中的扰动观测器和状态观测器合并为ESO,并保留图4的2–DOF内模控制的前馈控制环节,得到3–DOF的ADRC控制系统结构,如图7所示.
3–DOF的ADRC第1个自由度为参考信号发生器,其作用相当于模型跟踪控制系统中的参考模型,不仅用于安排过渡过程、处理被控系统输出超调性和快速性的矛盾,更重要的是可以采用参考信号发生器的参考模型来表示控制系统的设计指标,克服了最优控制中采用性能指标函数较难表示设计目标的问题;ADRC把参考信号发生器的参考模型作为控制系统的一部分,而控制器使被控对象的输出与参考信号之间的误差达到最小,间接实现了最优控制性能指标.韩京清先生还提出了TD及其多种具体形式来设计参考模型.ADRC的第2自由度为ESO,用于估计系统等效总扰动和系统状态;当把系统等效总扰动加入系统控制输入中实现总扰动补偿控制后,图7中虚线框将等效为一个近似积分串联型确定系统,为整个控制系统在外部扰动和内部参数变化下仍能保持良好控制品质奠定了基础.ADRC的第3自由度为基于状态误差的反馈控制率,具有PID控制基于误差反馈的优点,实现了图7中虚线框的等效近似确定系统的输出(即原被控系统的输出)跟随第1自由度的参考信号发生器的输出,从而实现控制目标.ADRC的3–DOF结构刻画了控制系统设计优化目标、实现了抗扰控制和误差收敛控制的分离和解耦,表面上看ADRC需要整定的参数比PID控制器的参数多,但由于ADRC三个部分可以根据系统性能和约束条件独立整定,实际上控制系统的综合和参数整定比PID控制器更加容易.
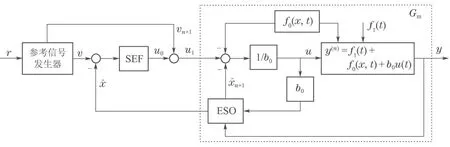
图7 具有3–DOF的ADRC系统结构Fig.7 System structure of ADRC with 3–DOF
下面以图7为基础分析ADRC的关键思想和其中体现的两种不变性原理.
5.1 被控系统的积分器串联规范型
ADRC采用积分器串联规范型来刻画被控对象的输入和输出关系[19],如式(25):
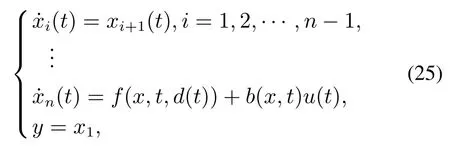
式中:u和y为被控系统的输入和输出,xi(i=1,2,···,n)是系统状态变量,n为系统阶次,xT=[x1···xn],f(x,t,d(t))是包含外扰d(t)在内的系统不确定项,b(x,t)为系统增益.
在非线性系统控制的微分几何方法中,当非线性系统满足一定条件时,也可以通过坐标变化和反馈线性化的方法化为式(25)形式,但是微分几何方法中要求非线性系统具有精确的数学模型;在非线性微分平坦系统控制方法中,采用微分代数方法也化成为式(25)形式,但是实际被控系统的微分平坦性比较难以验证,实际上,一些不满足微分平坦性的系统如欠驱动系统也是化为式(25)的,因此,式(25)具有普遍性,可以作为相当一大类非线性系统的典型描述.
把模型中的f(x,t,d(t))和b(x,t)的已知部分和未知不确定部分分开后有
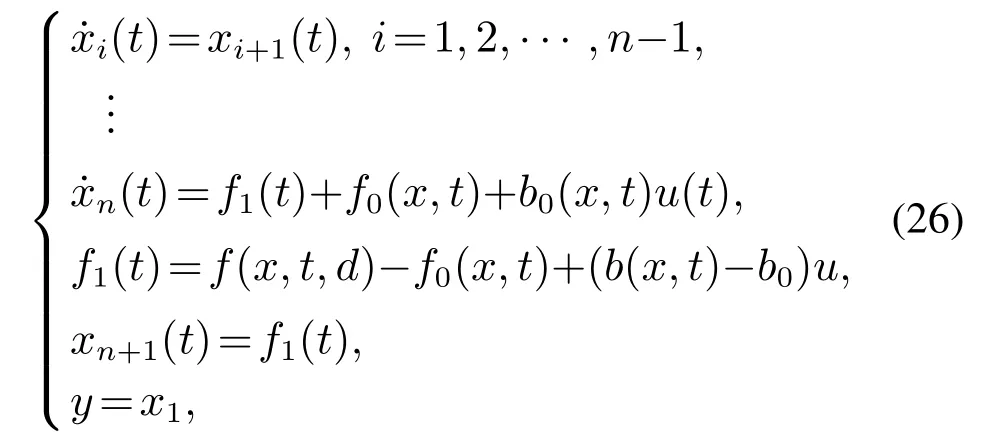
式(26)中:f0(x,t)和b0(x,t)≠0为已知,f1(t)为所有未知不确定部分的总和,称为在ADRC范式中称为系统等效总扰,是ESO中的扩张状态.式(26)的SISO积分器串联模型中,状态变量为系统的相变量,即输出y及其各阶导数,采用相变量作为状态变量为后续具有PID类型的状态反馈控制率提供了基础,系统的等效总扰动和系统的控制输入同时出现在n方程中,干扰和控制自然是匹配的,因此不存在控制量与干扰量的匹配问题.
积分串联模型只需要模型的阶次和对b的粗略估计即可,系统的不确定性归结为系统等效总扰动,而该总扰动由系统实际运行过程中的输入输出数据通过ESO实时估计出来,与参数自适应控制不同,ADRC并不需要产生总扰动的具体模型,因此,ADRC不依赖被控对象的精确模型,具有数据驱动控制的特点,一组ADRC的控制器和观测器参数可以适应一大类时变非线性控制系统.
5.2 ADRC范式中的算法
韩京清不仅提出了ADRC范式、系统等效总扰动和非线性积分串联模型,还给出了ADRC范式中每个自由度的高效实用算法.
针对第1个自由度的用于安排过渡过程的参考信号发生器,韩京清提出了如式(27)的TD:
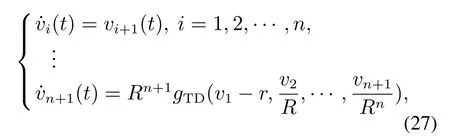
式中:R>1为使vi(t)跟随设定值r快慢的可调参数,称为TD的速度因子;gTD是使式(28)收敛到原点的任意函数,可为线性或者非线性函数,因此TD有包括最速TD、线性TD等多种形式.由于非线性可以实现有限时间收敛,因此在用于控制系统安排过程时,常用非线性有限时间TD.
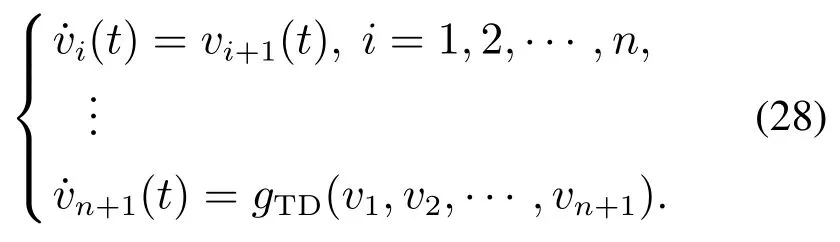
针对第2 个自由度,韩京清提出了对应式(26)的ESO,如式(29):

式中gi(i=1,···,n+1)为设计的函数,它使ESO稳定且1及其各阶导数收敛到x1及其各阶导数,特别地,收敛到f1.韩京清先生选取了一种具有较好收敛速度的函数,如式(30)所示:
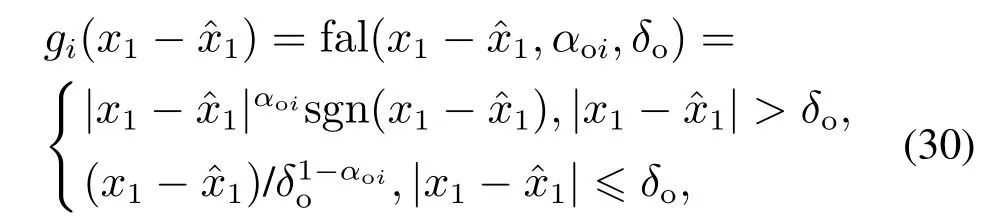
式中:0<αoi1,δo>0.特别地,当αoi=1时,得到线性ESO(linear ESO,LESO),如式(31)所示:

式中参数βi的整定可以采用高志强先生提出的带宽法来整定[20],设ωo为ESO的带宽,βi取二项式式(33)的系数.

理论和实践都表明,即使采用LESO也对式(26)的等效总扰动有很好的估计能力,这也是ADRC适用性强的一个重要原因.针对第3个自由度,韩京清提出协调第1自由度的参考信号产生系统和第2自由度的抗扰后的广义被控系统的NSEF,使广义被控系统的输出跟随参考信号,且满足一定的性能指标.
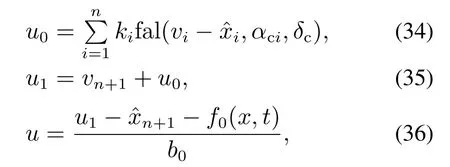
式中:ki为增益系数,可选0.5αci1,δc>0.特别地,当αci=1 时,得到线性状态误差反馈(linear state error feedback,LSEF)控制律,是一种PD(n−1)控制律.
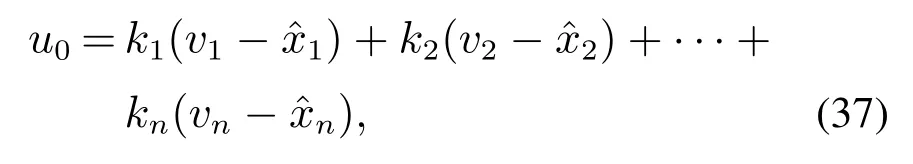
式中:参数ki的整定也可以采用高志强先生提出的带宽来整定[20],ωc为LSEF的带宽,ki取二项式式(39)的系数.
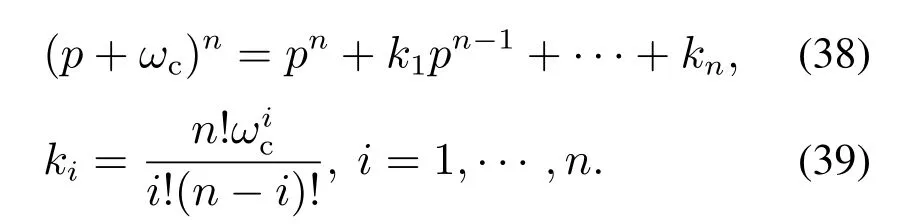
由于高志强先生的带宽整定LESO参数方法的提出,加速了ADRC的嵌入式系统芯片集成化和工业控制软件组件化的实现,为ADRC的大量应用提供了基础,ADRC能够一致地处理线性和非线性系统,即使采用线性ADRC也对非线性系统具有较好的适应性.陈文华先生在线性DOBC的基础上,提出了非线性DOBC[21],它可以较好地处理非线性系统的扰动问题,但是并没有像ADRC那样把系统的状态和扰动同时估计出来;非线性DOBC和ADRC的扰动估计能力和具体算法之间的关系将在今后的论文中讨论.
5.3 ADRC中的不变性
把式(36)代入式(26),并考虑ESO的收敛性[22–24]和ESO 经过一个短时的过渡过程之后有f1(t),则有

采用单位增益,提高了SEF控制器的可移植性.把式(35)代入式(41),有

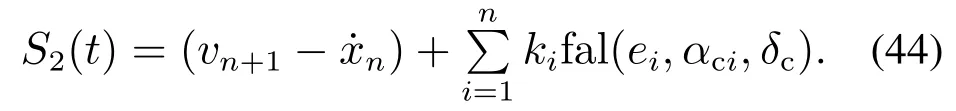
由前述参数ki的选择可知,S1和S2分别为稳定的线性滑动模和非线性分数阶滑动模,对于这两种滑动模,有定理1;在陈述定理1之前,先介绍准滑动模和准滑动模带宽的概念以及引理1.
由参考文献[22,24]离散系统的准滑动模和准滑动模带宽的定义,可以对连续系统(26)的准滑动模和准滑动模的宽度做类似如下定义.
定义1若系统(26)的运动状态构成的滑动模S(t)(如上述S1(t)和S2(t))满足|S(t)|ε(t),其中ε(t)0,则称系统的滑动模S(t)=0在其ε(t)邻域内作做准滑动模(quasi-sliding mode)运动,ε(t)称为准滑模的宽度(quasi-sliding mode band).
引理1给出了fal函数的性态.
引理1ADRC系列算法中的fal(z,α,δ)函数
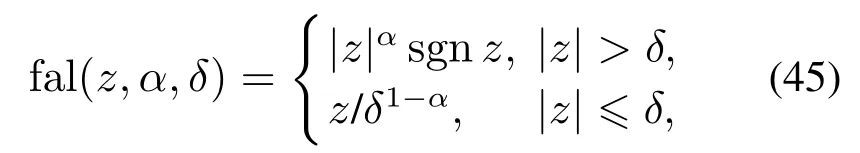
其中:z为实数,0<α1,δ >0,则下列不等式成立:
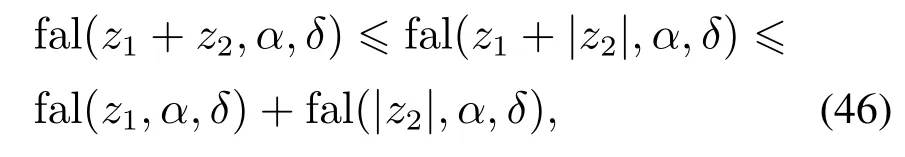
式中z1和z2为实数,且|z2|δ.
证为表示方便,令g(z)=fal(z,α,δ),则容易验证g(z)是连续和分段可导函数.
当z0时,有
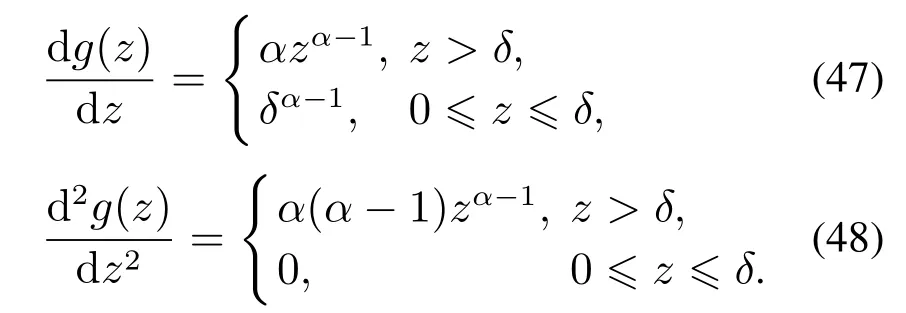
由于0<α1,δ >0,因此fal(z,α,δ)的一阶导数大于零,是增函数,二阶导数小于等于零,且在导数不连续点有左导数大于等于右导数,即有
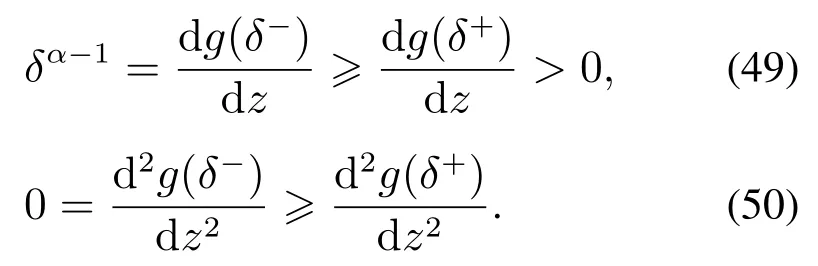
因此,当z0 时fal(z,α,δ)是凹函数;根据该函数关于原点的对称性,当z0 时fal(z,α,δ)为凸函数;fal(z,α,δ)在整个定义域内是单调增函数.
根据z1和z1+|z2|分别处于线性区和非线性区,共可以分成4种情况,证明过程中通过z=δ的点进行过渡.
1)当z1和z1+|z2|都处于线性区间时,由线性系统性质显然有
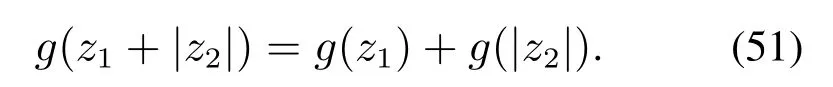
2)当z1处于线性区,而z1+|z2|处于非线性区间时,根据微分中值定理有
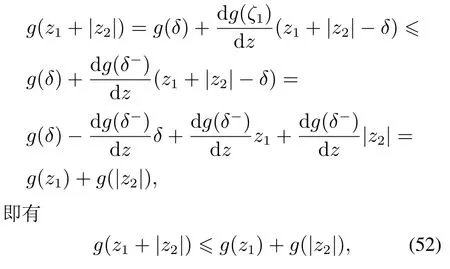
其中δζ1(z1+|z2|).
3)当z1处于非线性区间,而z1+|z2|处于线性区间时,一定有z1−δ,根据式(46)的线性系统的性质有
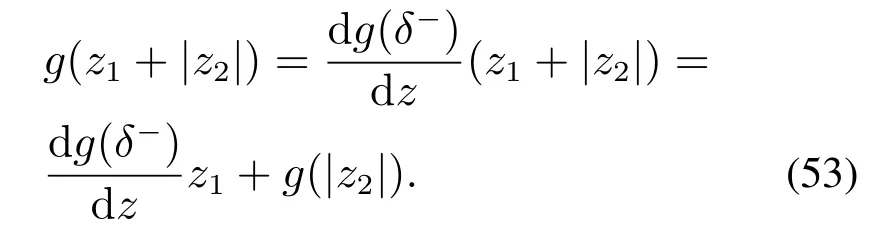
应用微分中值定理和式(50)–(51)有
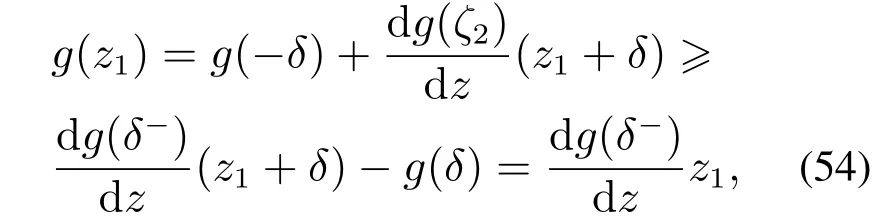
式中−δζ2z1.把上述式(55)代入式(54),可知式(53)成立.
4)当z1和z1+|z2|都处于非线性区间时,应用微分中值定理和式(50)–(51)有
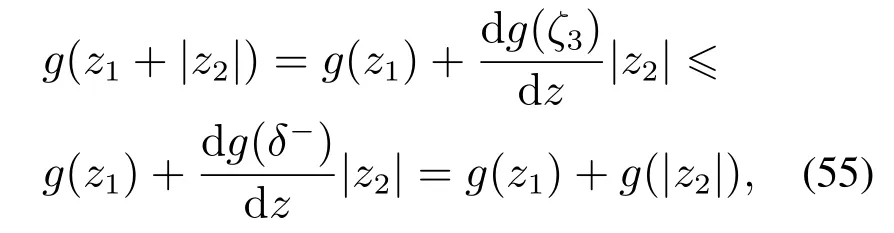
式中z1ζ3z1+|z2|.由g(z)的单调性和上述讨论可知最终有
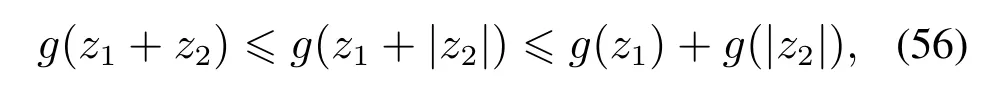
即式(47)成立. 证毕.
定理1在ADRC中,当采用TD安排设定值过渡过程、采用ESO(29)和LESO(31)进行系统状态和扩张状态进行估计时,采用如式(44)的非线性分数阶滑动模和式(43)的线性滑动模,则非线性反馈控制律SEF(34)和线性反馈控制律LSEF(37)可以实现系统(26)的准滑动模控制.
证由式(26)–(27)(35)和式(36)可得

在线性控制律(37)控制下,把式(37)代入式(57)中后再代入式(43)中有

由LESO(31)的收敛性[21,25–26]有

在非线性控制律(34)控制下,把式(34)代入式(57)中后再代入式(44)中有

由ESO(29)的收敛性[27]可知,在ESO运行一段时间后有则由引理1的式(46)有
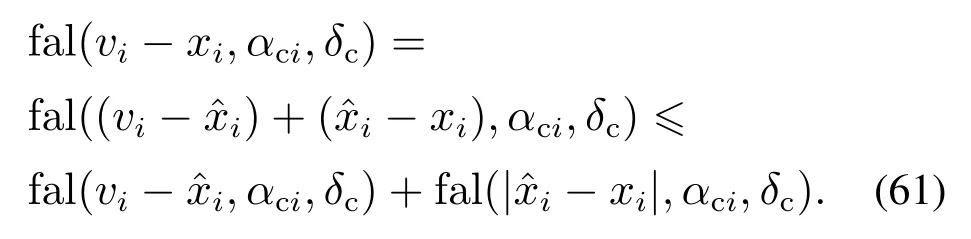
把式(61)代入式(60)有
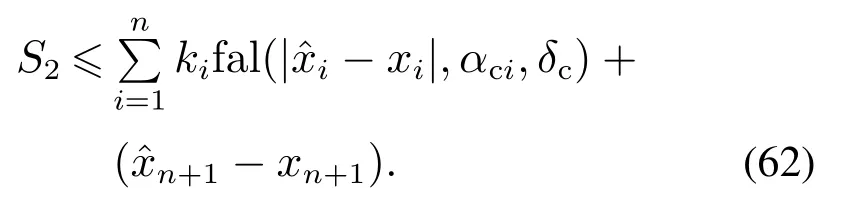
再由ESO(30)的收敛性[25–27]有
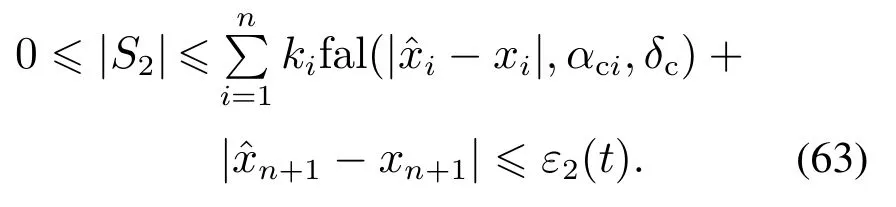
式(59)和(63)中的ε1(t)和ε2(t)表示ESO中系统状态和扩展状态估计误差绝对值的线性和非线性累加和,它们随着系统状态和扩展状态的估计误差趋于零而趋于零或者趋于原点的一个可接受的邻域范围,邻域大小由LESO和ESO的工作参数(如带宽)和被控系统的扰动频率确定;而SEF(34)和LSEF(37)的工作参数确定滑动面误差中每个分量的比例.因此,式(43)的S1和式(44)的S2的为滑动模控制的滑动模,而ε1(t)和ε2(t)为准滑动模的宽度,是一个时变函数,ADRC实现了在理想滑动模邻域内的准滑动模控制.
证毕.
注2工程实际中,ESO有一个收敛过程,特别在初始阶段时,当ESO的初始值与被控系统状态初始值相差较大时,往往会出现峰值现象(peaking phenomenon),此时的收敛性和也将出现峰值现象,离理想的滑动模比较远,避免峰值现象对控制的影响的有效方法之一是先投入ESO,待峰值现象过后,再投入控制.
ADRC通过ESO和SEF控制律实现了积分器串联模型不变性和全程准滑动模控制,因没有控制量的高频切换,不存在高频抖振现象,实现了对外部扰动和模型不确定的不变性、滑动模以外扰动的不变性.
6 结论
不变性原理是抗扰控制的基础,双通道前馈补偿实现了外部可测扰动作用下系统输出的不变性;内模控制和DOBC通过模型误差和滤波器来估计出作用于被控对象的等效干扰,并采用反馈补偿方式来抗扰使广义被控对象在扰动作用下保持为名义模型,实现了广义被控对象模型不变性;ADRC为3–DOF的控制系统结构,采用积分串联模型统一表示线性和非线性被控对象,通过ESO同时估计出系统状态(相变量)和总扰动,通过总扰动补偿实现在内扰和外扰作用下保持广义被控对象为单位积分器串联模型.双通道前馈补偿要求扰动可测量,且与内模控制和DOBC一样,都要求较精确的数学模型;ADRC对原有被控对象所需的信息量较小,适应性强,具有明显的数据驱动控制特征,能够通过嵌入式系统硬件和工业软件组件的方式来现实.此外,ADRC采用TD不仅安排了过渡过程,而且以模型的方式表示了控制系统的性能指标,SEF的状态误差反馈控制律实现了没有抖振的准滑模控制,保持了滑动模的不变性和鲁棒性.
从一般控制系统结构到内模控制,再到DOBC,最后到ADRC,虽然可以通过方框图等价变换方法变为相同或者相似结构,但是从物理意义上来说显然是不等效的.正是由于ADRC 采用积分器串联模型和3–DOF结构使得每个自由度具有明显的物理意义,实现了优化、抗扰和准滑模不变性的解耦,大大简化了工程实现和参数整定,特别是ADRC的带宽参数整定方法的提出,为大量普及ADRC在工业中的应用铺平了道路.再次验证了我国著名数学家冯康的名言“反映物质世界的一个物理问题可以有多个数学表达形式,这些数学形式在理论上是等价的,但在实践中未必等效.”[28–29]ADRC通过解耦解决了控制系统设计和综合中工业界所关心性能、抗扰和不变性等问题,缩小了控制科学与控制工程长期存在的鸿沟.
ADRC范式是一个开放的体系结构,除了韩京清先生给出的每个自由度的经典算法外,还有MFC的微分代数实现算法,它与经典ADRC算法的对比研究是下一步的工作;非线性DOBC是线性DOBC的重要发展,它与ADRC在非线性控制算法的内在联系和具体算法的区别也将在以后的研究工作中完成.随着ADRC范式和相关算法的理论研究的深入以及ADRC平台技术的多样化,ADRC将成为一种广泛使用的控制技术.
