基于高斯混合模型最大期望聚类的同时定位与地图构建数据关联
2020-04-11阮晓钢张晶晶朱晓庆
阮晓钢,张晶晶,朱晓庆,周 静
(北京工业大学信息学部;计算智能与智能系统北京市重点实验室,北京 100124)
1 引言
移动机器人同时定位与地图构建(simultaneous localization and mapping,SLAM)技术是实现机器人导航的关键,是指处于未知环境中的移动机器人从起始点出发,并利用自身携带的传感器不断感知,依照对自身的位置估计和获取的传感器数据信息,实现自身定位,同时在定位的基础上增量式的构建环境地图,实现机器人的自身定位和导航[1–3].数据关联(data association)是移动机器人同时定位与地图构建中的关键问题,通常也被称为一致性问题.
具体地,数据关联的目的在于判断在不同的时间和环境区域下,移动机器人携带的传感器通过对环境区域进行探测获得的测量值和已经存在的环境地图中的地图特征之间是否对应,并根据以上对应关系来判断其是否来自环境中相同的实体.少数的几次数据关联失败就会导致算法发散.所以,为保证SLAM状态估计的准确性,对数据关联的算法进行研究至关重要[4–5].
移动机器人同时定位与地图构建的相关研究领域中,应用相对比较广泛的数据关联方法有:独立兼容最近邻算法和联合相容分枝定界算法[6].独立兼容最近邻(individual compatibility nearest neighbor,ICNN)算法的优势是实现过程相对容易,并且具有较强的实时性,但是因为其未充分考量各个特征值的相关性,因而在所处环境发生变化的情况下容易受到较大影响[7].Neira 等人[8]提出的联合相容分枝定界(joint compatibility branch and bound,JCBB)算法相对于独立兼容最近邻算法的关联准确度得到了提高,但是在算法实现过程中的计算量较大,实时性也比较差[9].研究学者不断对数据关联算法进行优化,随后又相继提出了概率数据关联算法(probability data association,PDA)、联合最大似然(joint maximum likelihood,JML)、关联算法[10]和多假设跟踪(multiple hypothesis tracking,MHT)算法等[11],提高了移动机器人SLAM数据关联算法的计算效率并解决了多目标跟踪的数据关联问题.冯林等人[12]提出的基于动态阈值启发式图搜索的移动机器人同时定位与地图构建数据关联算法依据回溯思想实现了关联过程中的在线修正,并且为了能够尽可能的减小参与关联的数据量,对门限采用动态阈值的方法完成了过滤.王希彬等人[13]为解决SLAM的数据关联问题,提出了基于禁忌搜索的混沌蚁群算法.
为了改进JCBB算法,周武等人采用互斥准则和最优准则来提高关联的准确度,并自适应地进行分批数据关联[14].姚聪等人[15]引入K均值聚类算法对SLAM数据关联算法做进一步优化,根据K均值聚类算法对观测值进行聚类分组的联合兼容分支定界算法,确定分组数目时依据的标准是机器人所处的环境区域,这极可能将本应处于同一观测组的相邻路标错误的分在不同观测组,最终导致关联结果出现错误.刘丹等人[16]提出一种基于密度噪声的空间聚类分组(density-based spatial clustering of application with noise)的快速联合兼容分支定界的移动机器人同时定位与地图构建数据关联算法,关联准确度得到了提高并且算法的运行时间明显减少.
以上研究为SLAM数据关联算法的优化做出了贡献并提供了理论依据,针对当前SLAM数据关联算法联合兼容分支定界算法存在虽然关联准确度高但计算复杂,耗时长的问题,提出了一种基于高斯混合模型(Gaussian mixture model,GMM)的最大期望(maximum expectation,EM)聚类SLAM数据关联算法[17].首先选取局部地图并在局部区域内采用高斯混合模型的最大期望聚类算法对当前时刻的量测进行分组;其次,在每个观测小组中按照联合兼容分支定界算法对观测量和特征值进行数据关联以得到多组关联解;最后,通过整合上一步骤产生的各小组中观测值和已有的局部地图特征之间的关联结果,得到最优的关联解.算法通过对局部地图的限定和选取以及对观测值采用高斯混合模型的最大期望聚类算法进行分组.其优点在于:1)减少同一时刻参与关联的观测数量和地图特征数,从而从很大程度上降低了JCBB算法的计算复杂度;2)采用最大期望聚类算法,通过高斯混合模型为局部关联区域进行合理的聚类分组,无需根据环境凭经验获得,提高了算法的准确性.
2 SLAM数据关联模型
2.1 SLAM数据关联
移动机器人同时定位与地图构建技术不仅与机器人自身的状态有关,还关系到外界环境信息.同时定位与地图构建中的数据关联问题,具体涉及3种对应关系:携带环境感知传感器的移动机器人处于不同时间和不同的场合区域,其传感器获得的观测量之间的关系;获得观测量与已有的环境地图特征之间的关系;已有环境地图特征之间的关系.通过对比分析以上3种关系来确定观测量和特征值是不是来自环境区域内的相同实体,上述过程可以被看做是在应用观测–特征匹配特性来对环境状态空间进行搜索.机器人获得一个新的观测数据存在3种可能;一是为已构建环境特征信息;二是新的环境特征;三是虚景集合,即该观测值不是真实物理路标的反映,而是传感器噪声或镜面反射引起的.
假设机器人所处的环境区域内存在n个地图特征F=F1,F2,···,Fn,激光传感器测量到m个观测量Z=Z1,Z2,···,Zm.需要应用SLAM数据关联技术建立相关假设Hm=j1,j2,···,jm,用特征Fji来匹配每一个观测值Zi,当传感器测量值Zi与地图中的所有特征都不匹配时ji=0.其中,测量值Zi和相应的特征Fji是由测量函数fiji(x,y)=0相关联的,表明测量值和相应特征的相对位置必须是0.
2.2 联合兼容分枝定界算法
联合相容分枝定界(JCBB)算法是当前移动机器人SLAM研究领域常用的基于单个观测的独立匹配关联算法之一,算法实现过程中,联合相容检验方法用于把移动机器人获取的观测特征和地图特征完成联合关联,分枝定界方法则是用来对关联解空间进行搜索.
在关联假设集Hm=j1,j2,···,jm下,地图特征的联合观测方程表示如下:

联合新息为
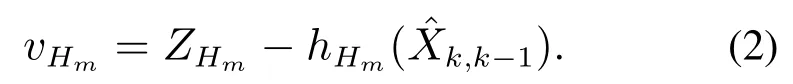
联合新息协方差可以表示为
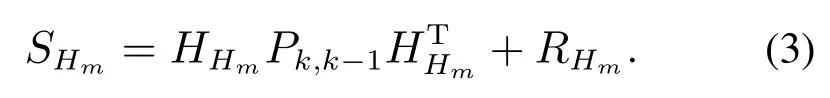
上述公式中:ZHm=[Zk,1···Zk,m],HHm=则联合相容的检测准则为下式成立:
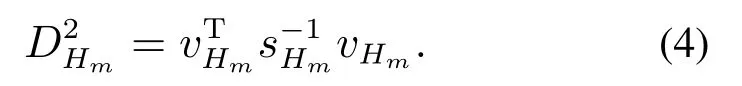
如果上式成立,则将所有观测特征和地图特征视为联合相容的.
在移动机器人SLAM数据关联问题中应用分枝定界准则的主要目的是对解空间进行遍历,并求得最优解向量.选取分支准则为式(4)的联合相容检测准则,然后根据其马氏距离来确定搜索顺序,并将整个关联解空间划分为多个子集;在划分出的各子集当中,定界标准的选取确立为观测特征和地图特征配对数目的单调非减规则,最后对解空间的最优关联解进行选取,选择配对数中最大的关联假设作为最终结果.
3 基于高斯混合模型的最大期望聚类分组
传统的联合兼容分支定界SLAM数据关联算法中的观测值解空间根据解释树模型进行描述,并采用了分支定界法结合相容性的递增式计算搜索以获取最优的数据关联结果,此过程中同时考虑到了全部传感器获得的观测值之间的相关性,因此数据关联结果的准确度比较高,并且鲁棒性较强.但是JCBB算法是将当前时刻观察到的所有观测值同地图中已有的环境特征进行关联,在大范围密集环境中,特征的数量随时间迅速增大,导致JCBB算法的计算量成指数增长、计算量大、复杂度高.可以通过减少同一时刻参与关联的观测数量和地图特征数使算法得到改善.对地图特征进行预处理,得到局部关联区域以减少同一时刻参与关联的环境特征数;还有就是采用最大期望算法,通过高斯混合模型为观测值进行合理的聚类分组以减少同一时刻参与关联的观测值数量.具体实现如下:
3.1 数据预处理
实际情况中,机器人每一步运动范围有限,距离观测比较远的特征可以被忽略,观测不需要和每个已知特征做数据关联,所以可以预先设定一个关联门限,把落在关联门限内的已知特征作为目标可能关联的对象.将关联门限值设置为r+d,r为移动机器人携带的激光传感器的有效扫描距离,d为补偿距离,补偿距离d的引入使得数据预处理后得到的局部地图能够尽可能全面的包含同传感器获得的测量值相匹配的环境地图特征.局部关联区域表示如下:

式中:(xf,yf)表示特征点的位置,(xr,yr)表示机器人位置坐标.如图1所示,关联的局部区域为以机器人为中心,以r+d为半径的虚线圆内的区域.圆点表示地图中已有的特征,星号表示传感器新观测到的观测值.通过预处理步骤获得局部关联区域,使得在某单一时刻参与移动机器人SLAM数据关联的环境地图特征数目得到有效减少.
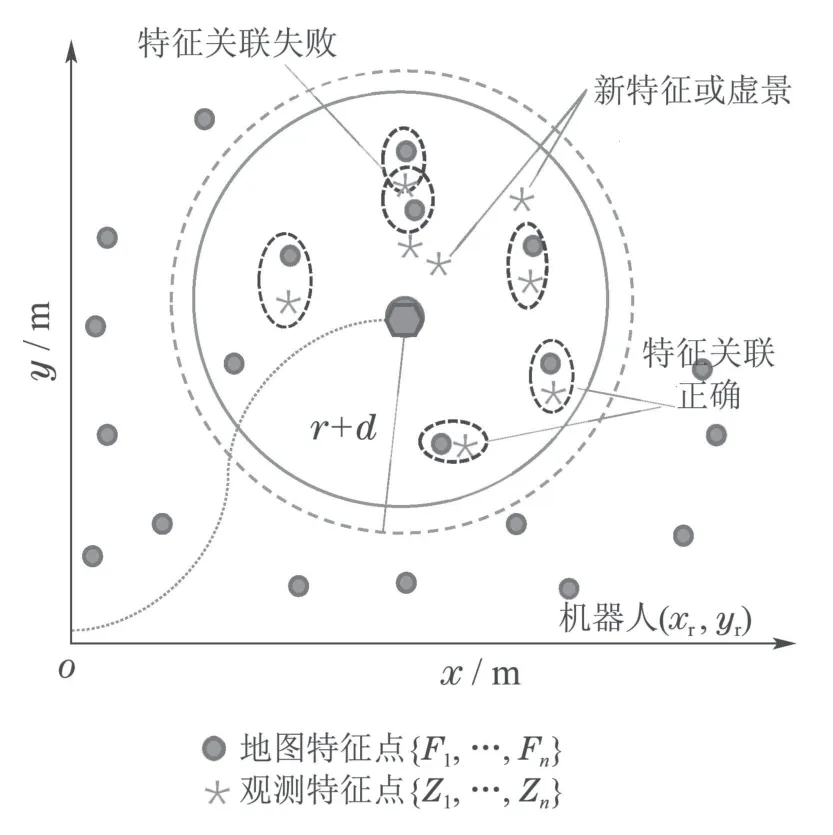
图1 数据关联示意图Fig.1 Data association diagram
3.2 基于高斯混合模型的最大期望聚类分组
移动机器人携带激光传感器在环境中行进,获得的观测值一般呈现出比较明显的分布,现将机器人观测到的特征值进行聚类分组.文[15]中应用K均值聚类算法对观测数据进行了分组,当整体观测值数据量较大时容易导致局部最优;与此同时,该算法在处理实际问题是对噪声和离群值(outliers)十分敏感,只用于numerical类型数据,非凸(non-convex)数据和不规则形状的聚类均不能通过该算法得到有效解决.于是文[16]就用density-based methods来系统解决这个问题.该方法不仅可以发现任意形状的聚类,还能够对存在噪声的数据进行比较准确的处理.基于密度的聚类方法取得的结果和用于识别聚类的固定参数有关,即使具有相同的判定标准聚类算法依然会受到稀疏程度的影响,也就是说,如果聚类相对比较稀疏则会被划分为多个类,反之如果密度较大,聚类将被合并为一个.所以,本文采用高斯混合模型最大期望(EM)算法对观测值及进行聚类分组.高斯混合模型(GMM)中的概率密度函数(probability density function)具有非常重要的作用,其能够简化数据的处理步骤,并将精确的处理结果分配至各Gaussian 混合成分中.GMM在对参数进行评估的过程中,应用了最大期望值算法(EM)进行处理,达到了改善数据分析运行效率的目的[18–19].

图2 数据关联聚类分组示意图Fig.2 The clustering grouping diagram of data association
首先将每一步观测到的特征值集合Z=z1,z2,···,zm和高斯混合成分个数k作为输入,然后进行高斯混合分布的模型初始化.高斯混合模型中k值的选取根据环境确定,根据激光传感器扫描到的观测值范围,一般选择分组的个数为3∼5 个.高斯混合分布(GMM)认为数据是从几个单高斯分布模型(GSM)中生成出来的,其中:µ是模型期望,σ是模型方差.即概率密度函数为
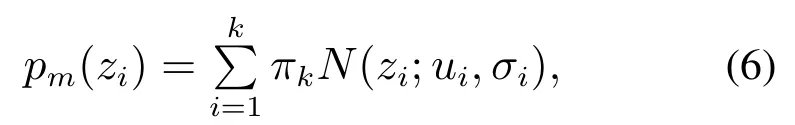
其中:πi >0是权值因子,表示选择第i个混合成分的概率,并且单个高斯分布N(z;µk,σk)表示高斯混合分布中的一个簇(component)分组,表示如下:

生成样本Z=z1,z2,···,zm的高斯混合成分用随机变量Q=qj(j=1,···,k)表示,qj的先验概率P(qj=i)对应于πi(i=1,···,k),根据Bayes 定理,现将根据第i个GMM生成的样本zj的后验概率密度函数表示为γji(i=1,···,k):
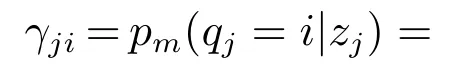
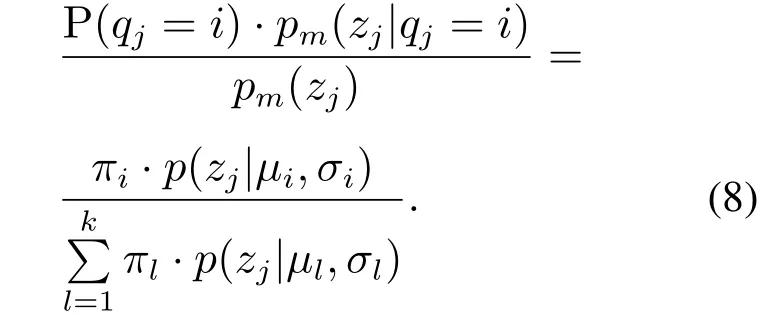
高斯混合聚类将观测特征集合Z划分为k个component,表示为Group={Group1,···,Groupk},每一个观测样本的component标记表示为
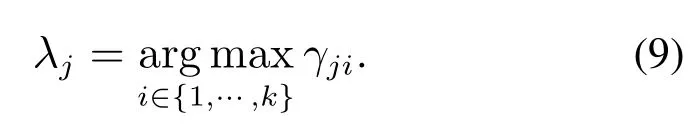
高斯函数(Gaussian function)的计算性能相对较好,高斯混合模型是具有k个聚类中心的聚类算法,如果系统中的样本分类是未知的,已知条件只给出样本点,能够计算出模型参数π,µ和σ,对于给定的观测数据集合Z,对其模型参数的求解可用极大似然估计.
激光传感器观测到的数据信息点数量为m个,并且服从某种分布pm(z;λ),算法的目的就是希望求得参数λ,以使生成数据点的概率实现最大化,这里的称为似然函数.一般情况下,单个数据点的概率值比较小,m个数据点的概率的乘积更小,非常容易发生浮点数下溢现象,因此,通常取似然函数的对数,变成称为log-likelihood function.GMM的log-likelihood function就是
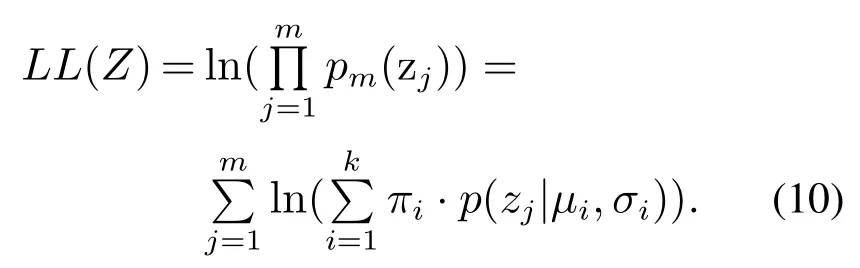
因此,可以应用最大期望值算法对观测数据集模型进行迭代优化求解,随后根据已经完成训练的模型区分观测值数据样本所属的分类.具体步骤表述为:首先从k个簇分组中随机选取一个(其中任意一个簇被选中的概率用权值因子πk来表示);随后将观测值数据样本代入上一步选取的簇中,并判断该数据样本是否属于此类别,若不是则重新选取簇分组.
Expectation步骤:假设模型参数已知,求隐含变量Q分别取q1,q2,···的期望,也就是Q分别取q1,q2,···的概率.此步骤在高斯混合模型中就是求观测值样本数据点由每一簇分组生成的概率γji.
Maximization步骤:考虑根据最大似然方法(maximum likelihood method)求取模型参数.将Expectation操作步骤求得的γji看做是观测值样本数据点zi由第k个簇分组生成的概率.如果参数πi,µi,σi能够令LL(Z)最大化,那么由得
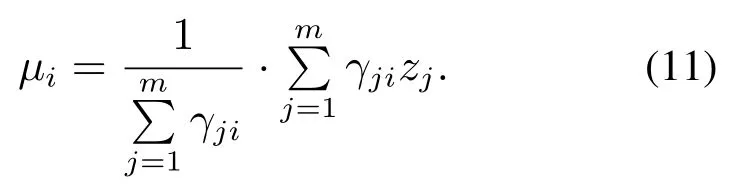
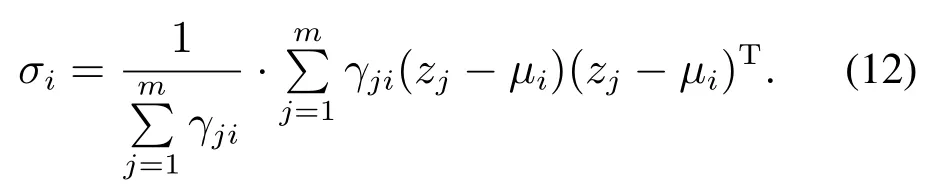
权值因子πi >0且使其最大化LL(Z),求得
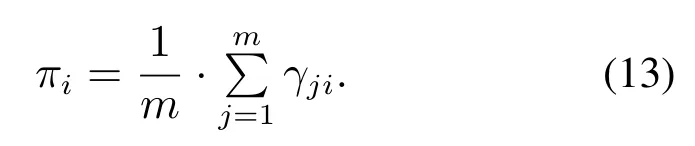
根据式(11)–(13)更新模型参数,并根据式(9)确定zj的component标记λj,将zj划分到相应的component,即最终得到component的划分结果Group={Group1,···,Groupk}.
在移动机器人运动的每一步,通过GMM–EM算法将所有的观测值分成若干关联度小的分组.然后对每一个分组采用JCBB数据关联方法从而得到局部关联结果Groupk,每一个分组表示为解释树中的一层,Groupk为这一层中的节点.从该解释树中选择最联合相容的匹配对作为最终的关联结果,本文称该算法为GEMJCBB.算法描述如图3所示.
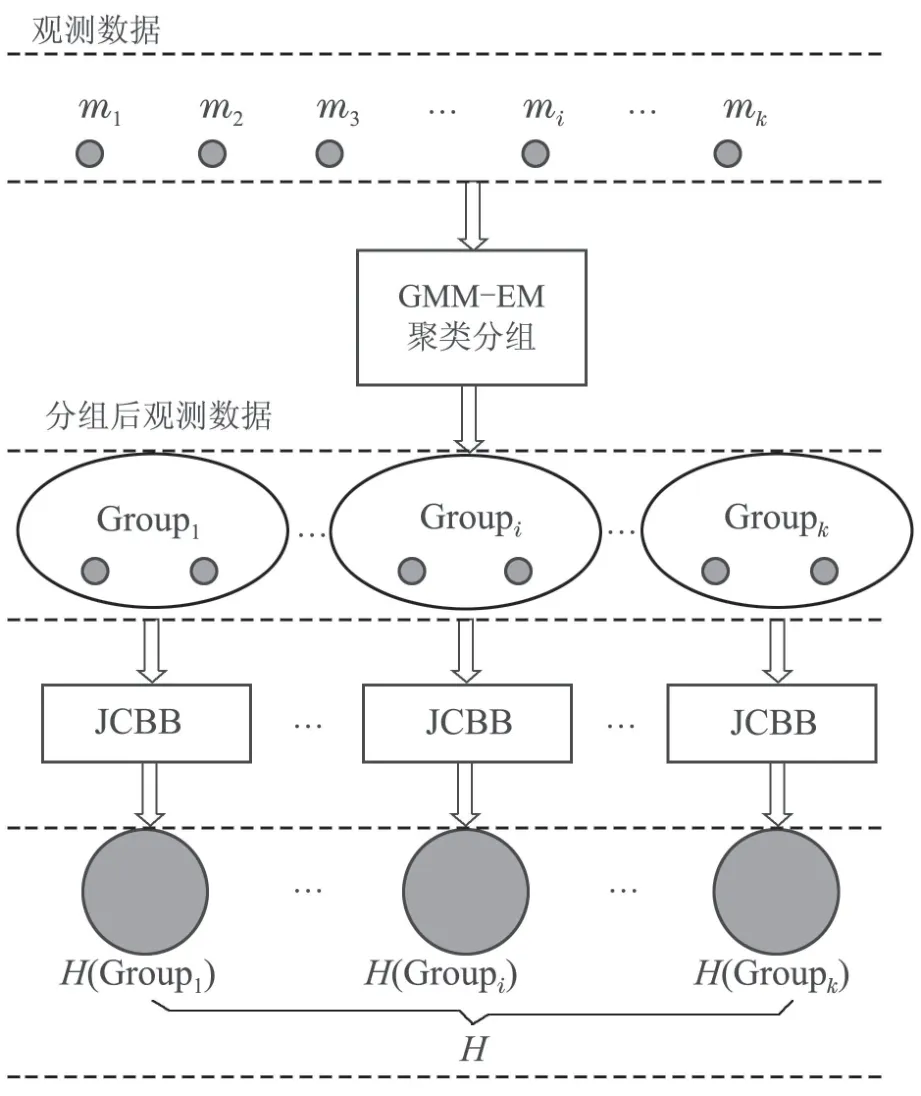
图3 GEMJCBB算法流程图Fig.3 GEMJCBB algorithm flow chart
4 仿真结果及分析
为了验证本文提出的SLAM数据关联算法在不同环境中获取关联结果的高效性和准确性,利用Bailey等人开发的SLAM算法模拟器[20]设计了如图4–5所示的仿真环境.仿真环境1尺寸大小为160×160 m2,仿真环境2尺寸大小为240×240 m2.图4–5中:实线为机器人的实际路径,“◦”为路标点,“∗”表示环境中实际存在的特征.将本文提出的GEMJCBB算法同JCBB算法,KJCBB算法,DFJCBB算法分别从定位精度,算法运行时间长短以及关联性能等方面进行了对比分析.
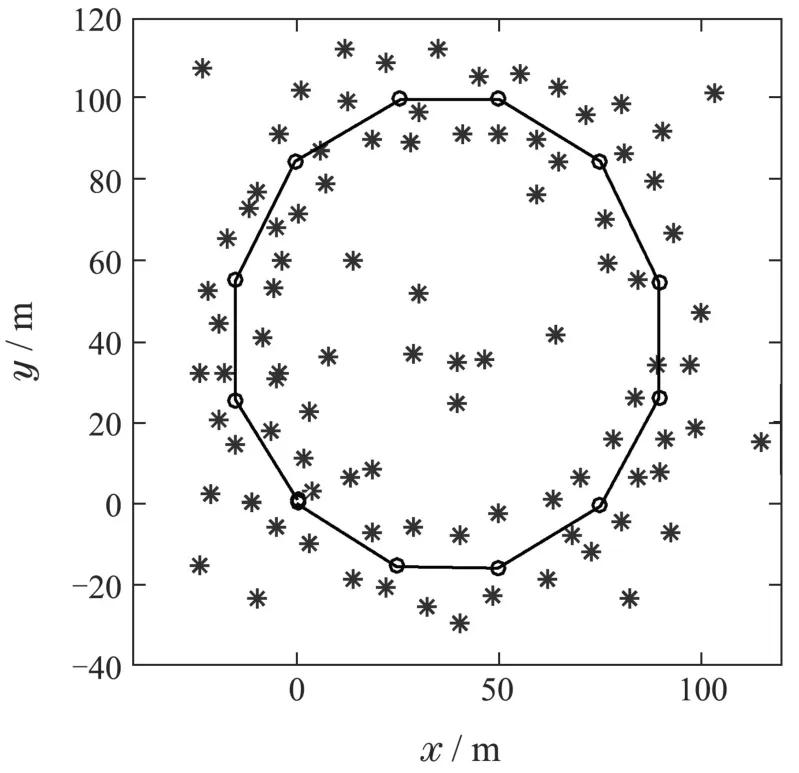
图4 仿真环境1Fig.4 Simulation environment 1
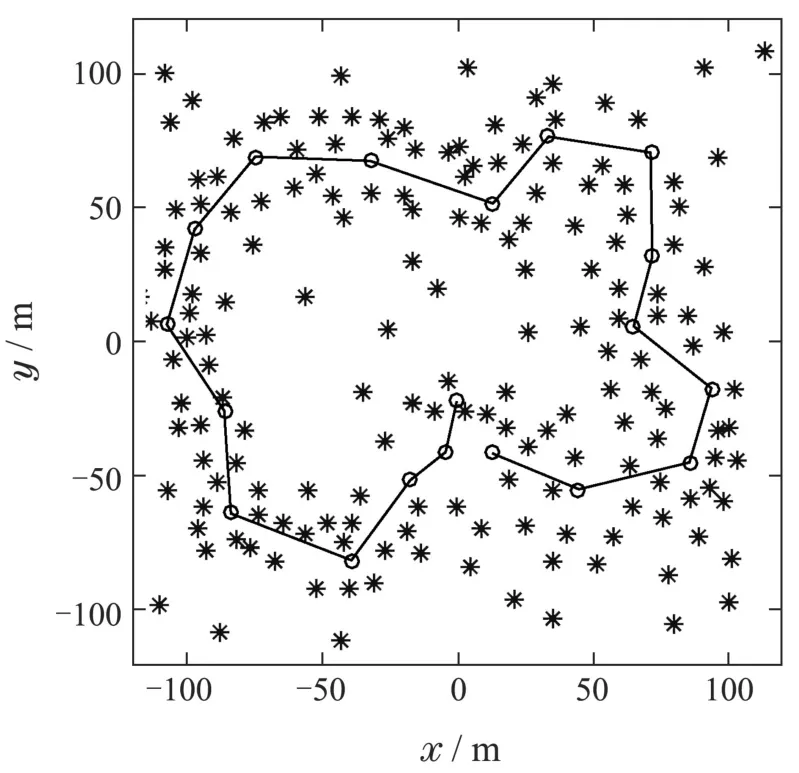
图5 仿真环境2Fig.5 Simulation environment 2
4.1 路径拟合效果比较分析
图6–7中:蓝色实线为机器人的实际路径,绿色“∗”表示环境中实际存在的特征,红色“◦”为预测特征,黄线表示估计路径.其中图6是仿真环境1下的数据关联及路径拟合效果图,如图6(a)–(d)所示,分别为JCBB算法、K均值聚类和JCBB的数据关联算法,DFJCBB算法和本文提出的高斯混合模型–最大期望值聚类JCBB算法在仿真环境1中的数据关联和路径拟合结果.仿真环境1 的拐角比较平滑,可以看出图6(d)中机器人所得到的预测观测值与实际的环境特征几乎都吻合.而且都是一个预测观测值对应匹配一个环境特征,且路径跟踪拟合的效果更好,其定位精度更高,数据关联的准确性更好.
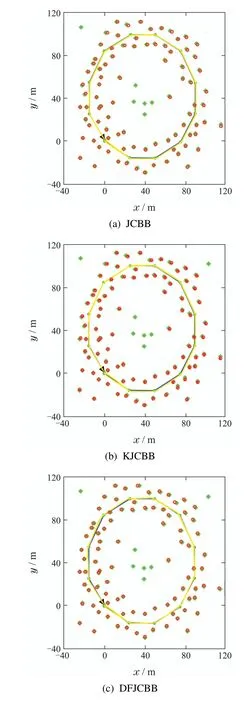
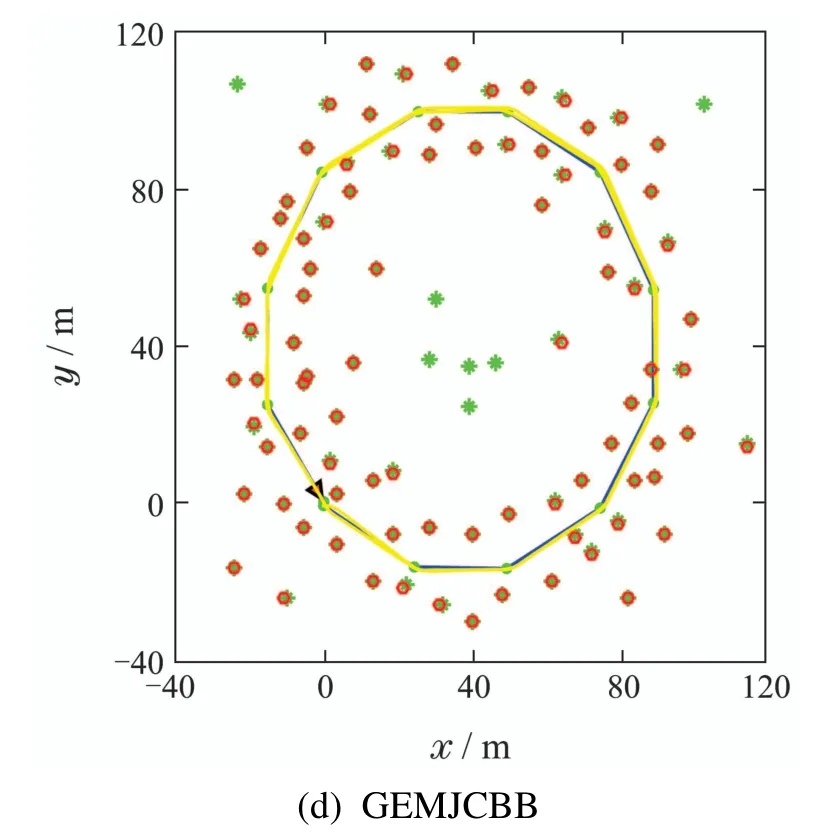
图6 仿真环境1下的4种方法数据关联效果图Fig.6 Four data association methods in simulation environment 1
在仿真环境2下验证4种算法的区别,图7(a)–(d)分别为JCBB算法、KJCBB算法、DFJCBB算法、本文提出的GEMJCBB算法的路径拟合结果.

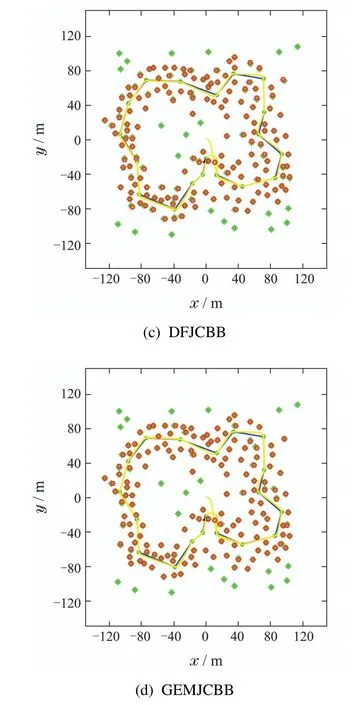
图7 仿真环境2下的4种方法数据关联效果图Fig.7 Four data association methods in simulation environment 2
由于环境中尖角设计的特殊性,在拐角后的路径拟合出现些许偏差,通过观察比对可以看出,本文提出的算法路径拟合效果更好.
为了能够更加精确的比较基于4种数据关联算法路径拟合的精度,分别绘制了如图8、图9的位姿估计误差曲线,位姿估计误差曲线分别描述了在仿真环境1和仿真环境2下实际路径和估计路径的X轴和Y轴方向的误差.在仿真环境1中基于JCBB,KJCBB,DFJCBB,GEMJCBB算法的SLAM在X轴方向的平均估计误差分别为0.2308,0.2278,0.1997,0.1894;在Y轴方向的平均估计误差分别为0.3040,0.2033,0.1798,0.1721.在仿真环境2 中基于JCBB,KJCBB,DFJCBB,GEMJCBB算法的SLAM在X轴方向的平均估计误差分别为1.0845,0.8071,0.6707,0.6581;在Y轴方向的平均估计误差分别为0.4314,0.3019,0.2539,0.2452.通过仿真实验结果可知,本文提出的基于GEMJCBB的SLAM数据关联算法提供了更加可靠的关联结果,使SLAM的位姿估计精度较其他3种算法得到了提高.

图8 仿真环境1下的路径拟合误差Fig.8 Path fitting error in simulation environment 1
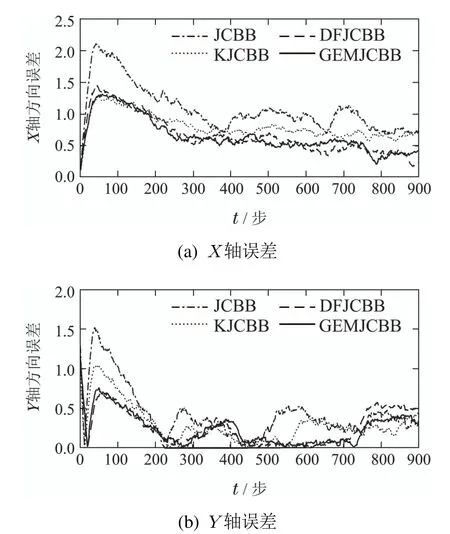
图9 仿真环境2下的路径拟合误差Fig.9 Path fitting error in simulation environment 2
4.2 算法运行时间对比分析
在仿真环境中,机器人从初始状态开始逆时针匀速移动,分别对基于GEMJCBB以及上面提到的3种关联算法的SLAM进行20次蒙特卡洛仿真实验,下表显示了4种关联算法的关联时间以及基于这4种算法的SLAM 运行总时长.由运行结果可知,本文提出的GEMJCBB–SLAM数据关联算法在仿真环境1中的算法平均运行时间为137.3047 s,平均关联时长为119.3047 s;在仿真环境2 中的算法平均运行时间为207.4528 s,平均关联时长为188.6390 s.对仿真实验结果进行分析可知,本文提出算法的平均运行总时长和关联时长均小于其他3种算法.具体地,KJCBB,DFJCBB和GEMJCBB 3种算法均对观测量进行了分组,降低了联合兼容计算中观测量的维数,进而降低了计算的复杂度;同时,GEMJCBB算法采用高斯混合模型(GMM)最大期望值(EM)算法对观测值进行聚类分组.GMM中的概率密度函数能精确的将观测样本数据分配到各个混合成分中,并简化数据处理步骤.同时,GMM在评估参数时参考了EM算法思想,使算法的数据分析速度得到了明显的提升.并且本文提出的GEMJCBB算法在数据预处理操作中划定了局部关联区域,减少了同一时刻参与数据关联的环境特征数量,所以进一步提高了算法的效率.

表1 仿真环境下算法运行时间对比表Table 1 Algorithm running time comparison table in simulation environment
4.3 关联性能对比分析
在分析算法的关联性时引入二分类问题,将实例划分为两类,即正类(positive)或负类(negative).评价数据关联性能用到的4个指标:TP(ture positive)为真正类,表示检测到的正确的观测–特征匹配对数;TN(ture negatives)为真负类,表示检测到的新环境特征个数;FP(false positive)为假正类,表示检测到的错误的观测–特征匹配对数;FN(false negatives)为假负类,表示没有检测到的正确的观测–特征匹配对数.当前时刻的观测数目表示为Total:

正确率(Precision)表示预测为正的样本中预测正确所占的比率,计算如下:
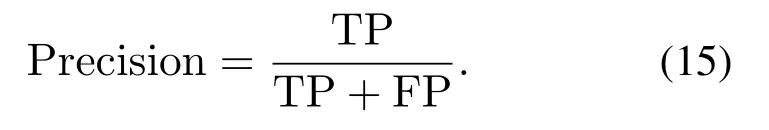
召回率(Recall)、真正类率(true positive rate,TPR),表示判对样本中的正样本率,即检测到的正确的观测–特征匹配对数占总观测–特征匹配对数的比例,计算公式为

准确率(Accuracy)是众多评价指标中比较常见且容易理解的,定义为被分对的样本数与总样本数的商,一般情况下,Accuracy数值越高效果越好.计算公式为
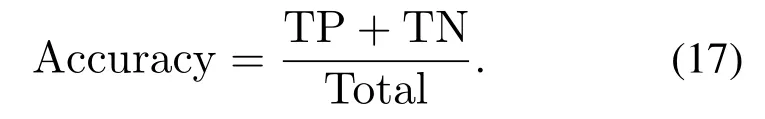
4种算法的关联准确度平均值见表2,本课题中提出的算法的关联准确度高于其他3种算法.为了更加全面而科学的评价算法,再次对4种算法进行综合考量,常见的方法F–Measure,又称为F–Score.F–Measure 是Precision和Recall加权调和平均:

当参数α=1时,就是最常见的F1Score,也即
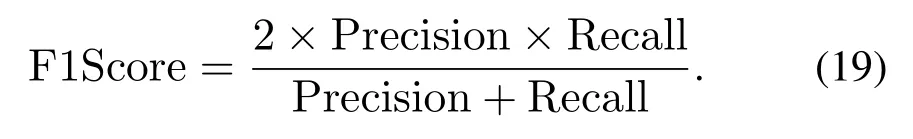
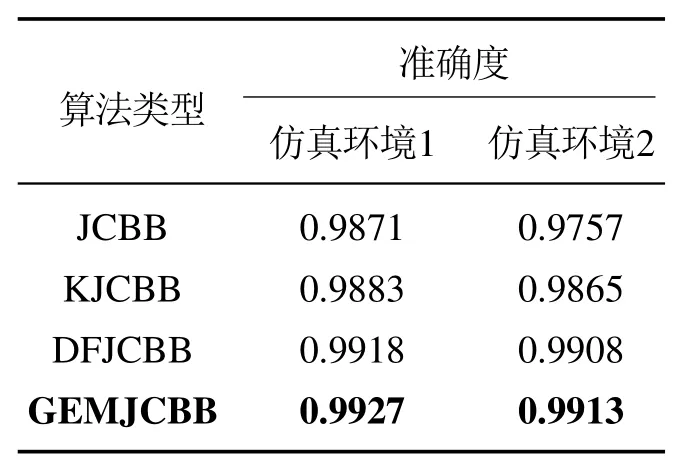
表2 仿真环境下算法关联准确度对比表Table 2 Correlation accuracy comparison table of algorithms in simulation environment
F1Score 综合了Presicion 和Recall 的结果,当F1-Score较高时则能说明方法比较有效.图10即为两个仿真环境中,分别用4种关联算法进行数据关联的F1-Score.由图10可知,本文提出算法在仿真环境1下的F1Score值较其他3种算法得到了提高,在仿真环境2下,由于拐角幅度较大,4种算法在运行过程中的F1-Score值均有所下降,但本文提出算法没有值过低的情况,在4种算法的运行效果中依然比较好.

图10 仿真环境下的F1ScoreFig.10 F1Score in simulation environment
5 结论
数据关联是移动机器人同时定位与地图构建中状态估计问题的前提和基础,是其中的重点和难点问题,联合兼容分支定界(JCBB)算法是目前能够得到可靠关联结果的常用的SLAM数据关联算法,但是在大范围密集环境中,参与关联的地图环境特征和观测值的数量随时间迅速增大,导致JCBB算法的计算量成指数增长,导致计算复杂度高.实际应用中,要求好的数据关联算法在准确度高的同时,还需具备实时性好、计算复杂度低的特点.本文提出一种基于高斯混合模型的最大期望聚类的SLAM数据关联算法,通过减少同一时刻参与关联的观测数量和地图特征数使算法得到改善.首先对地图特征进行预处理,得到局部关联区域以减少同一时刻参与关联的环境特征数;其次采用EM算法,通过高斯混合模型为观测值进行合理的聚类分组以减少同一时刻参与关联的观测值数量.随后将局部关联区域内的环境特征值与聚类分组后的观测值分别进行关联.实验结果表明,本文提出的基于高斯混合模型最大期望值聚类分组联合兼容分支定界算法获得了准确的关联结果,同时降低了计算复杂度,提高了算法效率,为移动机器人SLAM中的定位问题提供了可靠的保障.
