与抛物线变换有关的问题之赏析
2020-04-10王兴凯
理科考试研究·初中 2020年4期
王兴凯


摘 要:抛物线的平移、轴对称、旋转变换体现着运动变换的理念与思想,对发展学生的空间观念与思维品质有很大帮助,这类试题兼顾学情与升学考查,给不同的学生以适度的层梯,使不同层级的学生能各有收获,属中考热点题型之一.
关键词:抛物线;图象变换;数形结合;分类思想
将二次函数知识融入其他知识之中,融入的方式是以变换综合为主.以二次函数为载体的变换类综合题通常会设置图形经过变换后是否存在线段关系,面积、周长最值,是否存在等腰三角形、直角三角形、相似三角形、特殊的四边形等基本问题,考查相似、勾股定理、二次函数最值、几何变换性质、数形结合、分类讨论、变化和对应、方程和函数等思想方法.这类综合题主要包含抛物线内的几何图形的变换和抛物线本身的变换两大类.本文以后一类型为例撷取相关试题加以浅析.
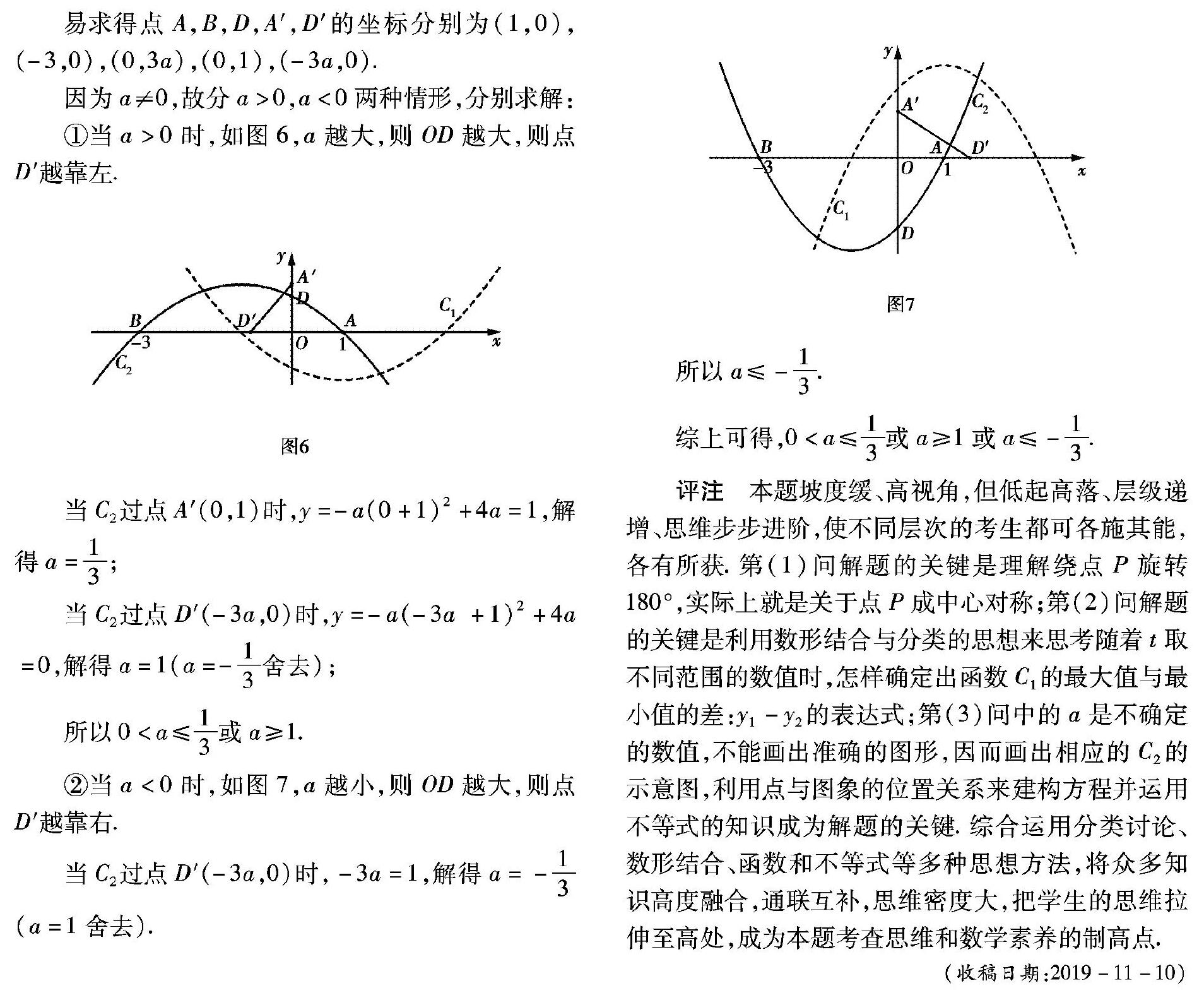
评注 本题坡度缓、高视角,但低起高落、层级递增、思维步步进阶,使不同层次的考生都可各施其能,各有所获.第(1)问解题的关键是理解绕点P旋转180°,实际上就是关于点P成中心对称;第(2)问解题的关键是利用数形结合与分类的思想来思考随着t取不同范围的数值时,怎样确定出函数C1的最大值与最小值的差:y1-y2的表达式;第(3)问中的a是不确定的数值,不能画出准确的图形,因而画出相应的C2的示意图,利用点与图象的位置关系来建构方程并运用不等式的知识成为解題的关键.综合运用分类讨论、数形结合、函数和不等式等多种思想方法,将众多知识高度融合,通联互补,思维密度大,把学生的思维拉伸至高处,成为本题考查思维和数学素养的制高点.
(收稿日期:2019-11-10)
