钱塘江涌潮对地形变化的响应研究
2020-04-10张舒羽潘存鸿程文龙
张舒羽,潘存鸿,程文龙
(1. 浙江同济科技职业学院,浙江 杭州 311231; 2. 浙江省水利河口研究院,浙江 杭州 310020)
钱塘江涌潮汹涌磅礴,具有极高的欣赏价值,是独特的自然遗产和宝贵的旅游资源。钱塘江涌潮形态多样,如海宁的交叉潮、盐官的一线潮、老盐仓和美女坝的回头潮;涌潮激越时排山倒海,涛声震闻数十里外。由于涌潮迅猛、潮强流急,如2003年后现场实测最大测点涌潮流速为6.65 m/s,最大垂线平均涌潮流速为5.58 m/s[1],强大的涌潮动力直接影响沿江建筑物和航运的安全。因此,探索涌潮的规律,研究涌潮的水力特性和产生机理,对于涌潮保护和防护具有重要的学术价值和现实意义。
江道地形是影响涌潮强弱的重要因素之一。吴维庆[2]和Mahmood等[3]指出钱塘江沙坎引起的潮波变形是涌潮产生的直接原因。杜勇[4]指出水深越浅,涌潮越容易形成。潘存鸿等[5]指出河床地形通过影响潮汐大小间接影响涌潮高度,钱塘江尖山河段主槽走北时,潮差大,涌潮强,主槽走南时,潮差小,涌潮弱。毛献忠和龚春生[6]采用数学模型在不改变河势的基础上将钱塘江闸口至大缺口平水年的地形平均抬升和降低1.5 m,模拟了枯水地形和丰水地形下潮波的变化规律,指出枯水地形下,低潮位抬升,不利于潮波传播,一定程度上降低涌潮高度;丰水地形下,较利于增大涌潮高度。张静怡等[7]通过引进局部地形指数,在长江口北支水道建立了局部地形指数与青龙港涌潮平均涨率之间的良好相关关系。Shi等[8]基于概化河口模型,采用理论分析和数学模型计算分析了河口水深和河宽变化对涌潮的影响,发现水深和河宽的减小促进涌潮的产生。
根据实测江道容积和潮位资料研究,钱塘江涌潮的强弱与江道季节性冲淤及年际冲淤有密切的关系。年内洪季过后江道容积大,涌潮强度也大;丰水年,江道容积大,涌潮也强。钱塘江涌潮的形成与其特殊的沙坎地形有关。而世界上有很多的河口海湾,有的潮差比钱塘江还大,却没有涌潮,如俄罗斯Mezen河,潮差为7.8 m,未见涌潮现象[9]。
在上述成果基础上,为进一步分析涌潮强度与地形的关系,采用涌潮数学模型模拟了钱塘江8种地形下涌潮的变化规律,得出在一定范围内,涌潮随地形的下降而增强,但当超过某一临界值后,涌潮强度反而会减弱。这可解释钱塘江丰水地形涌潮大、枯水地形涌潮小的现象。为使涌潮具有观赏性,维持适当的江道容积是必要的。
1 二维涌潮数学模型
1872年,Boltzmann提出了著名的分子运动论的控制方程,Boltzmann方程描述的是分子速度分布函数的时空变化。通过建立微观、宏观变量的基本关系,求出水流宏观变量。
无碰撞的二维Boltzmann方程为[10-11]
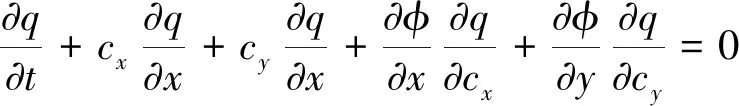
(1)
外力作用项φ考虑非平底引起的重力、阻力、风应力、柯氏力和盐度密度引起的压力等外力。
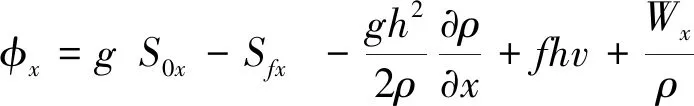
(2)
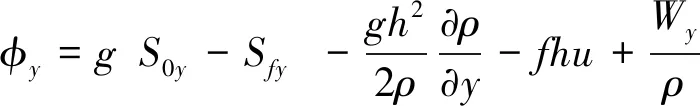
(3)
式中:q为平衡态时分子速度分布函数;cx、cy分别为分子在x、y方向的分子速度;g为重力加速度;S0x、S0y分别为x、y方向的底坡项,Sfx、Sfy分别为x、y方向的阻力项;ρ为盐水密度;f为柯氏系数;Wx、Wy分别为x、y方向的风应力。
将式(1)乘以(1,cx,cy)T,并对分子速度空间积分,可得控制方程:
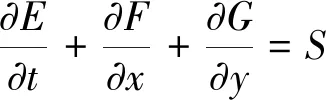
(4)
式中:
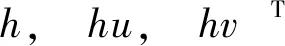
(5)
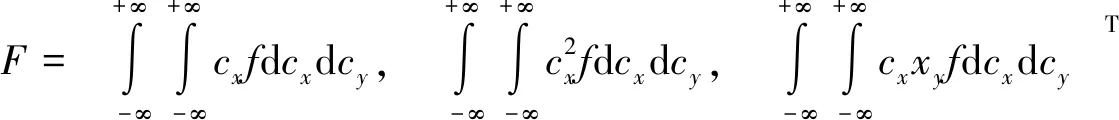
(6)
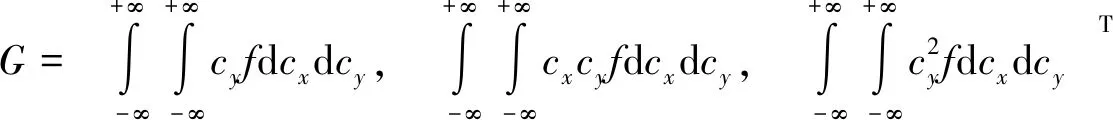
(7)
S=[0,gh(S0x-Sfx),gh(S0y-Sfy)]T
(8)
计算域采用三角形进行剖分,并采用网格中心格式。设Ωi为第i个三角形单元域,Гi为其边界,对方程式(4)应用有限体积法离散,经推导可得基本数值解公式[10, 12]
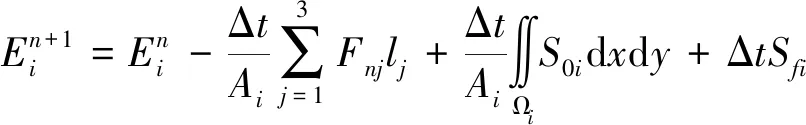
(9)
式中:Ai为三角形单元Ωi的面积;Δt为时间步长;Fn=Fcosθ+Gsinθ,(cosθ,sinθ)为Гi外法向单位向量;下标j表示i单元第j边;lj为三角形边长;上标n为时间步。
求解式(9)的核心是法向数值通量的计算、底坡源项的处理,以及动边界处理,详见文献[10, 13]。
2 涌潮数学模型验证
2.1 计算网格和边界条件
富春江电站多年平均流量952 m3/s,澉浦多年平均潮差5.64 m,最大潮差9 m。模型的范围及网格布置见图1。计算上边界取在富春江电站,边界条件给流量过程;下边界为澉浦,边界条件给潮位过程。固壁边界条件为滑移边界,法向流速为零。模型采用三角形无结构网格,共布置了142 263个单元和73 616个节点,网格最小步长50 m,时间步长0.5 s。验证时段澉浦最大潮差7.8 m,富春江电站下泄流量400 m3/s。
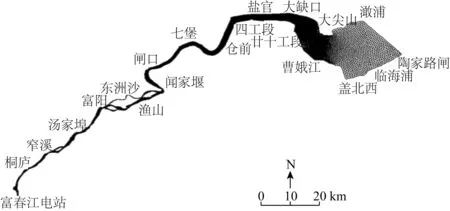
图1 钱塘江涌潮计算网格Fig. 1 Computational grid of tidal bore in Qiantang River
2.2 涌潮河段潮位流速验证
水文验证资料采用2010年10月实测数据,该测次采用ADCP对盐官、丁桥(盐官下游7.7 km)、胡斗(盐官上游约8 km)进行了涌潮观测,并收集水文站闸口、七堡、仓前、盐官的同期潮位资料。验证地形采用2010年7月的实测地形资料。验证结果表明,高低潮位及潮位过程的计算值与实测值符合较好,流速流向过程计算值与实测值吻合良好,模型能很好地捕捉到涌潮间断过程。限于篇幅,仅列代表站位的验证情况于图2~图4。经验证率定,涨潮时曼宁系数取0.004,落潮时取0.006~0.012。
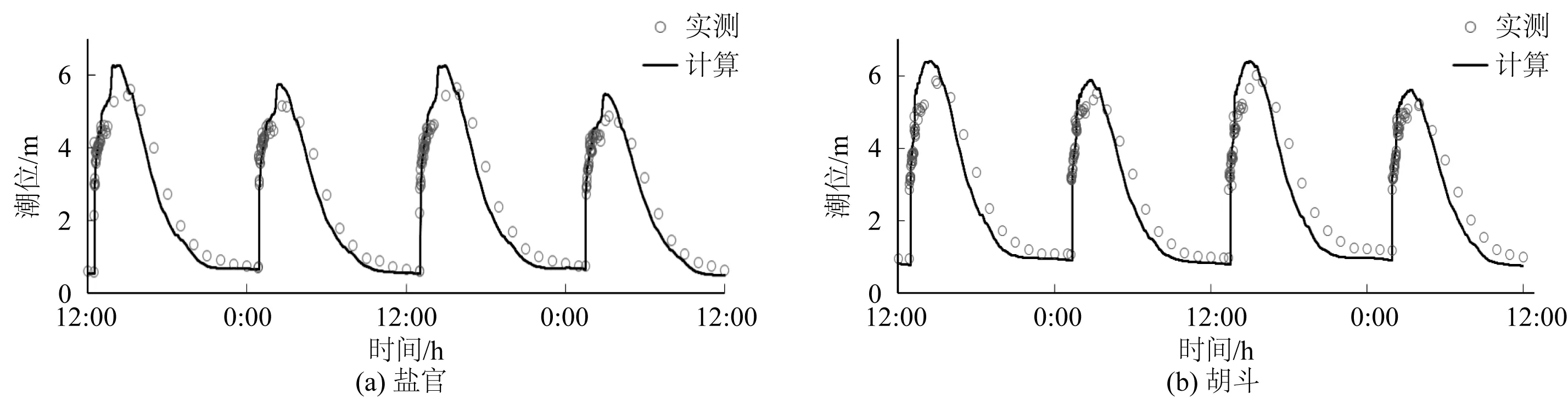
图2 代表站位潮位验证Fig. 2 Verification of tidal level at representative stations

图3 盐官站流速和流向验证Fig. 3 Verification of flow velocity at Yanguan station
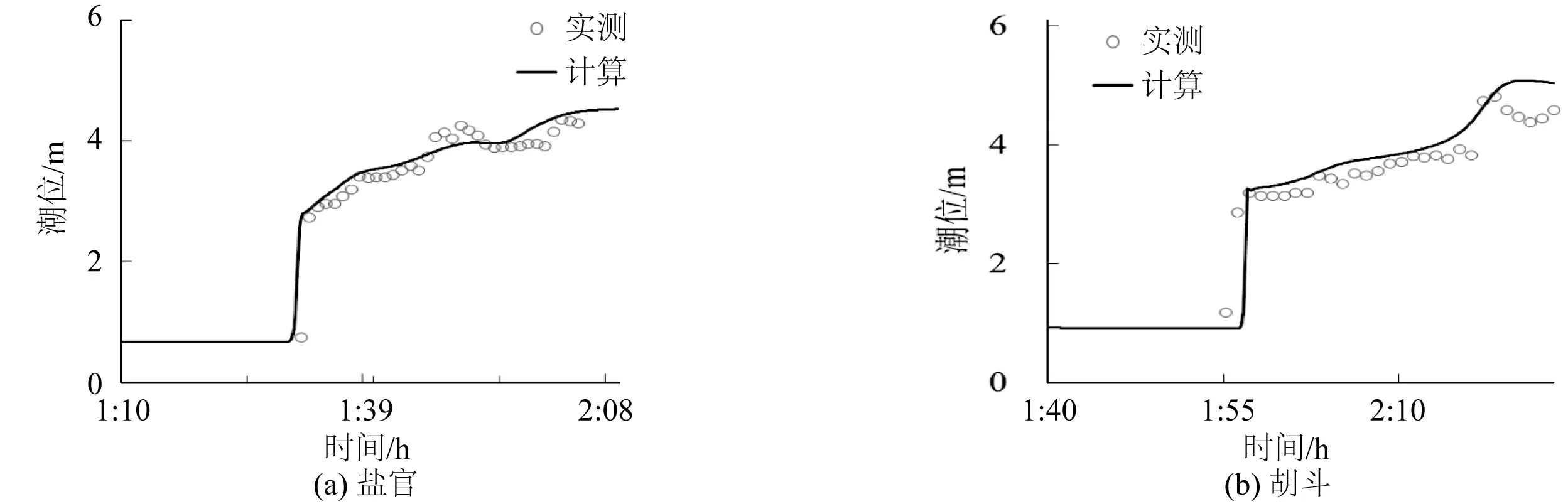
图4 涌潮前后潮位验证Fig. 4 Tidal level verification before and after tidal bore
3 潮汐和涌潮特征沿程变化
根据验证得到的参数计算富春江电站枯水流量500 m3/s、澉浦最大潮差7.85 m、江道容积偏丰(4.54亿 m3)条件下的涌潮,并分析其涌潮特征。
3.1 潮汐特征沿程变化
钱塘江河口潮汐特征沿程变化见图5。钱塘江河口水下存在庞大的沙坎,沙坎顶部位于七堡附近。自澉浦至七堡,河床快速抬升,低潮位也迅速抬升。七堡以上,河床呈倒坡下降,低潮位抬升幅度趋缓。高潮位沿程变化较小。下游潮差大,上游潮差小。钱塘江河口潮汐为半日潮。潮波在传播过程中前波变陡,后坡变缓,涨潮历时缩短,落潮历时延长,涨潮历时远小于落潮历时。
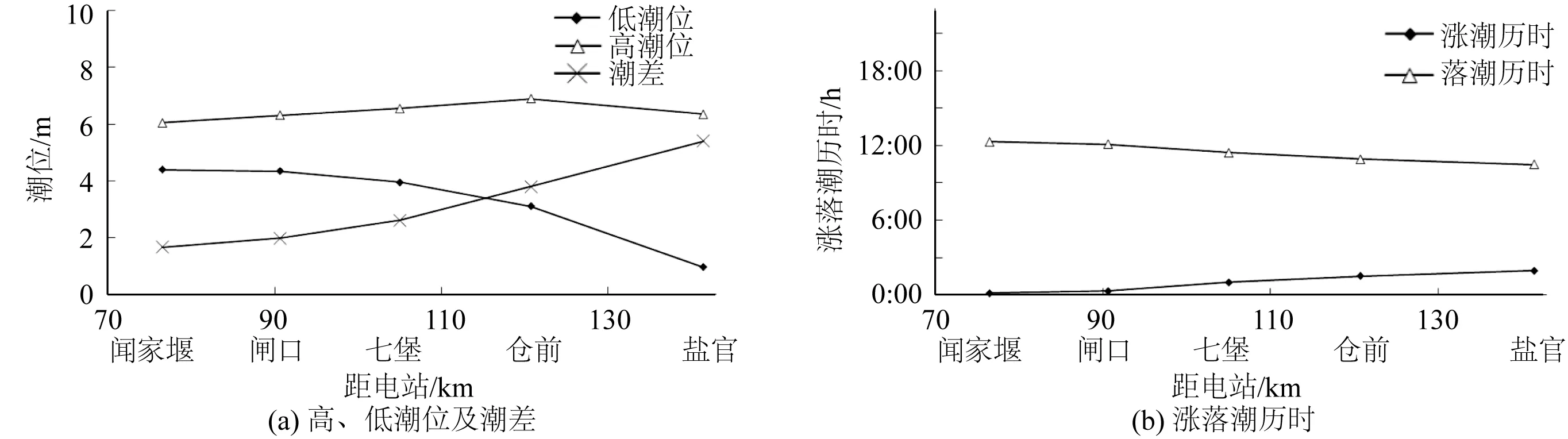
图5 潮汐特征值沿程变化Fig. 5 Changes of tidal characteristics along the river
3.2 涌潮特征沿程变化
表征涌潮特性的指标有涌潮高度、涌潮最大流速、涌潮传播速度、涌潮潮景和涌潮陡度等。图6绘出了前三个指标的沿程变化。
涌潮高度是指潮头水面顶面与潮端前趾低水位的水位差,这里采用连续时间内水位的急剧抬升高度。偏丰水年,闻家堰~盐官涌潮高度在1.0~1.8 m间。
涌潮过后的流速是全潮过程中的最大流速,为涌潮流速。涌潮河段流速的特点是涨潮流速大,变化快;落潮流速小,变化缓。图7绘出了数模计算所得的盐官河段最大流速平面分布图,最大流速普遍达到4~5 m/s以上,最大达到7 m/s以上。
涌潮传播速度指涌潮潮头的前进速度。根据文献[5]涌潮传播速度c为:
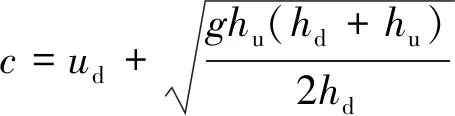
(10)
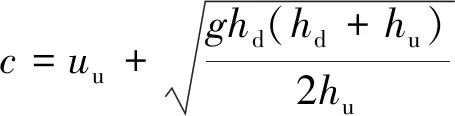
(11)
式中:h为水深;u为流速;下标d和u分别标识下游侧(涨潮方向)和上游侧(落潮方向)。
由数模计算得到ud、hd、hu,根据式(10)或(11)计算得到涌潮传播速度。涌潮传播速度自盐官3.9 m/s至闻家堰10.5 m/s沿程增大。
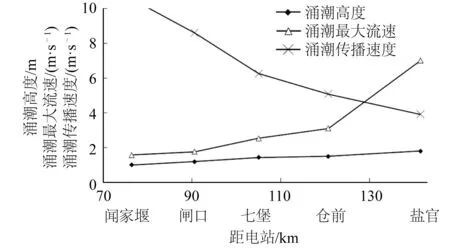
图6 涌潮特征值沿程变化Fig. 6 Changes of tidal bore characteristics along the river
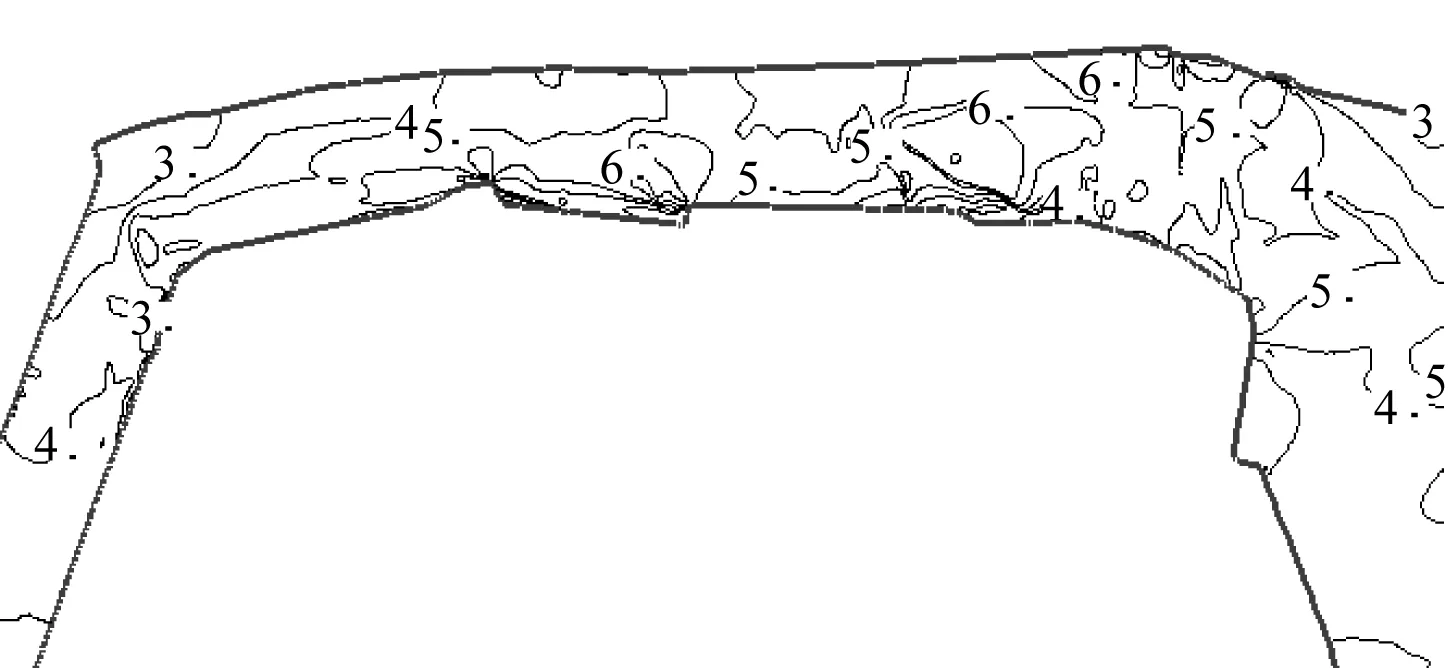
图7 盐官河段最大流速分布(单位:m/s)Fig. 7 Distribution of maximal velocity at Yanguan reach
图8绘出了每间隔半小时沿程水面线的变化。可见涌潮到达时,水面迅速抬升如壁立。
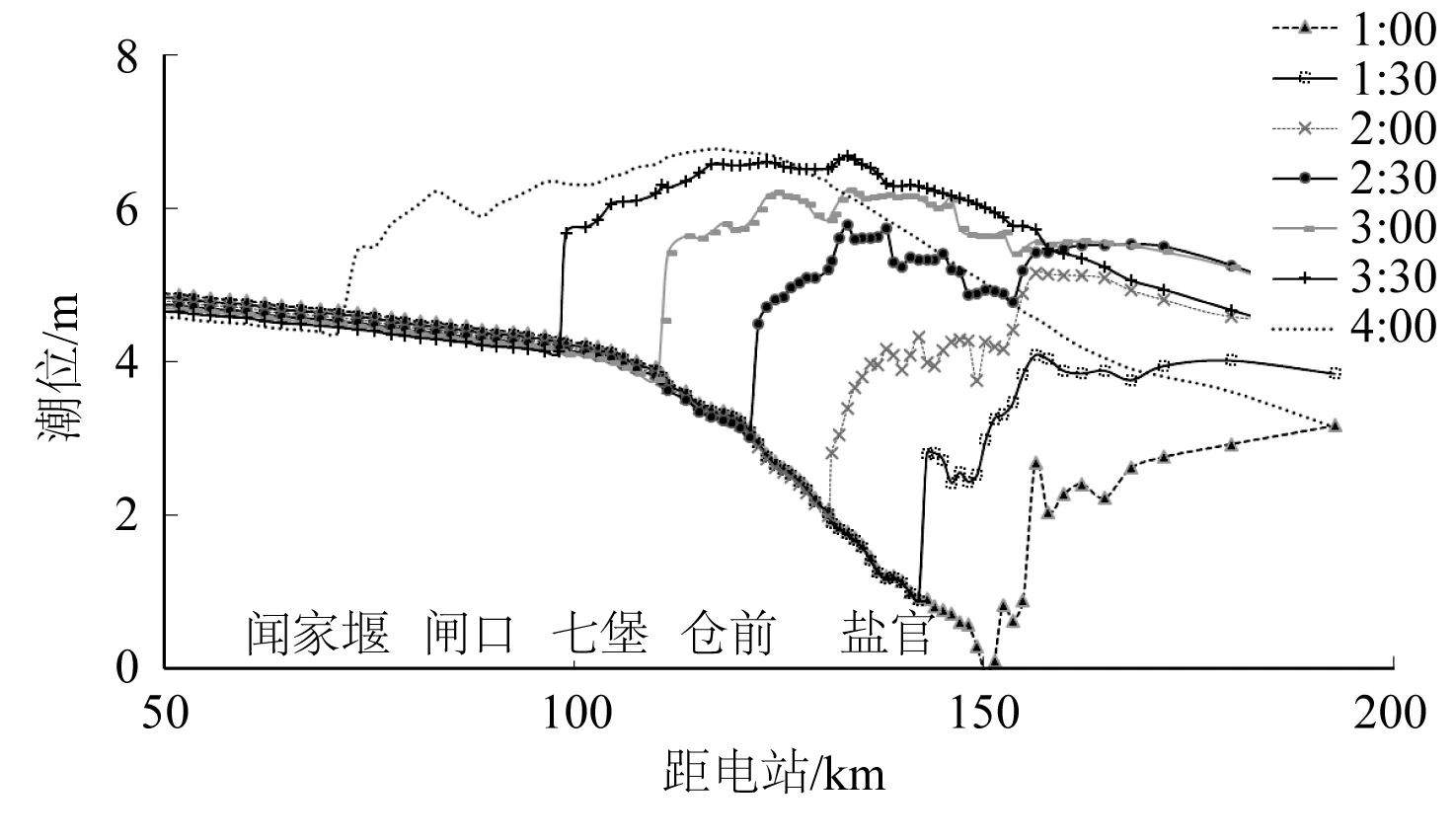
图8 不同时刻水面线Fig. 8 Water surface line at different time
钱塘江涌潮在传播过程中形成变化多样的涌潮潮景,如“交叉潮”“一线潮”和“回头潮”。江道相对顺直的盐官河段形成“一线潮”。涌潮行至老盐仓,涌潮走向与堤线几乎正交,涌潮被反射,形成“回头潮”。“交叉潮”发生在尖山河段分汊河势下,在模型中要求网格空间步长要小,较难模拟。本次数模复演了盐官“一线潮”和老盐仓“回头潮”。
4 地形对涌潮特征的影响
钱塘江河口自澉浦至闻家堰河床冲淤多变,尤其是盐官以上河段,地形受径流丰、枯影响明显,历史上实测5.2 m以下盐官~闸口江道容积最大容积为10.62亿m3(1955年7月)、最小为2.53亿m3(1969年2月)。1980年后,盐官以上大规模治江缩窄工程基本结束,江道冲淤变化减小。盐官~闸口江道最大容积为6.26亿m3(1995年7月)、最小为2.80亿m3(2004年11月)。根据实测资料,一般认定3.0亿m3、4.0亿m3、5.0亿m3分别代表枯水、平水和丰水江道的典型容积。
为分析地形对涌潮的影响,在原计算地形(江道容积4.54亿m3,偏丰地形)的基础上进行整体抬高或降低,共设置8种方案,即在原地形抬升1 m、降低2 m、4 m、5 m、8 m、9 m、12 m,对应于江道容积3.54亿m3(偏枯)、6.54亿m3(丰水)、8.54亿m3、9.54亿m3(接近历史最大)、12.54亿m3、13.54亿m3、16.54亿m3。
4.1 地形对潮汐特征的影响
图9和图10为8种不同地形条件下钱塘江沿程潮位和潮差变化。地形对钱塘江河口的潮汐影响很大,特别对低潮位影响明显。由于江道宽浅水深小,地形降低使江道容积显著增加,低潮位迅速降低,当地形下降9 m后,此时水深已较大,低潮位较低。对于高潮位,地形降低一方面引起沿程高潮位下降,另一方面江道容积增大,纳潮量增大,潮汐动力增强,高潮位抬高。高潮位受此2方面共同影响,变化复杂。随着地形的降低,钱塘江沿程潮差基本呈增大趋势,涨潮历时增加,落潮历时缩短。以盐官站为例,地形在抬升1 m至降低5 m时,对应潮差从4.58 m增大到10.07 m,随着地形进一步降低12 m,潮差减小到9.62 m;而涨潮历时随着地形的降低一直增大,从1∶33增大到6∶22。七堡、仓前、闸口、闻家堰的潮差、涨落潮历时变化也有同样的规律。
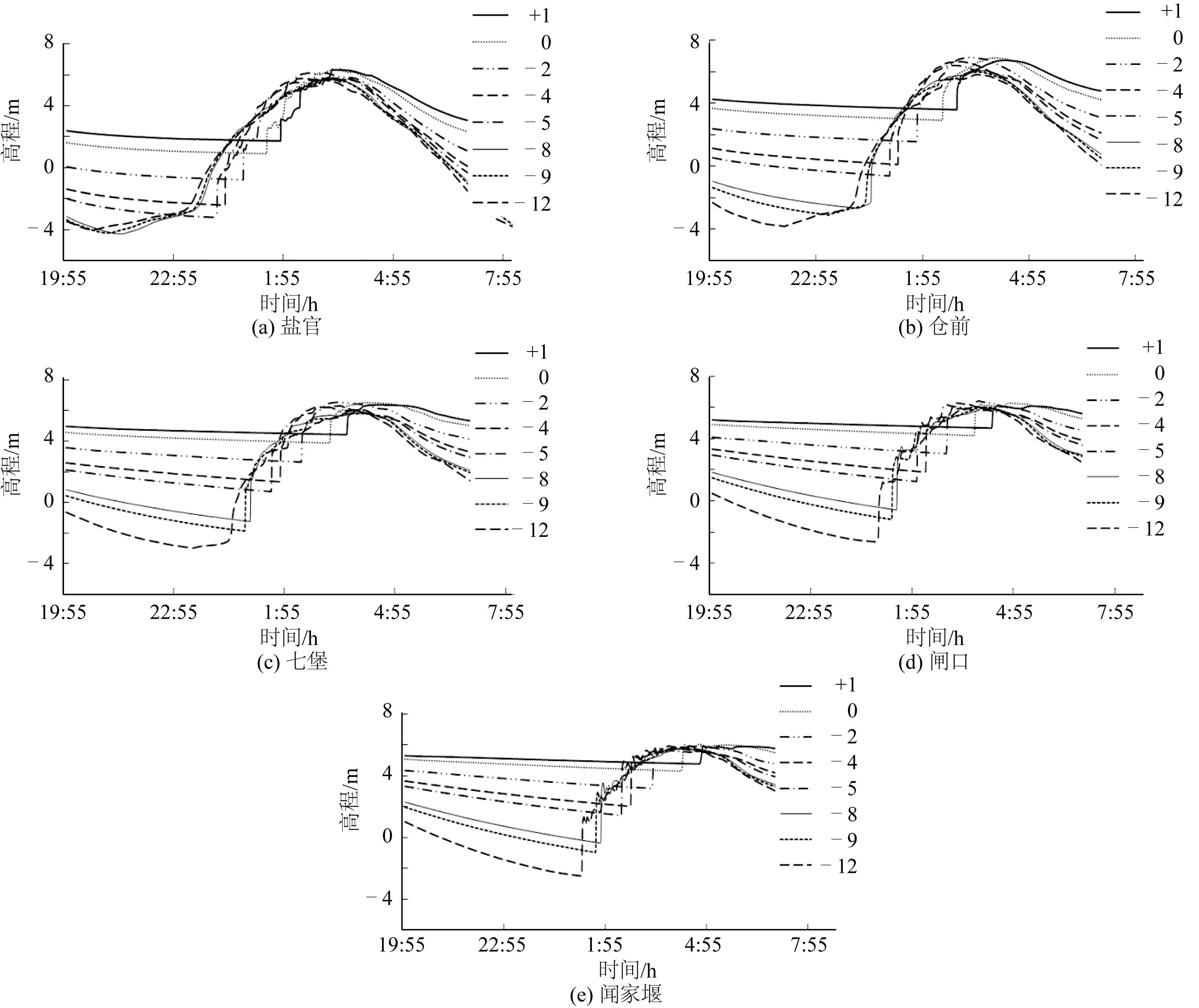
图9 不同地形下沿程潮位变化Fig. 9 Tidal level variation along the river under different topographies
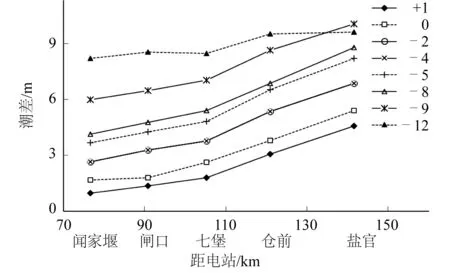
图10 不同地形下沿程潮差变化Fig. 10 Tidal range variation along the river under different topographies
4.2 地形对涌潮特征的影响
4.2.1 涌潮高度变化
地形降低,河道纳潮量增加,潮差增大,有利于涌潮的形成,但是涨潮历时延长,潮波变形减缓,又不利于涌潮的形成。观察地形、涌潮高度之间的关系,发现随着地形的降低,各站涌潮高度呈先增后减的规律(见图11)。以盐官为例,地形从抬升1 m至降低4 m时,涌潮高度从1.22 m增大到2.58 m,达到最大,而后随着地形继续降低,涌潮高度减小。地形降低8 m后,涌潮消失。
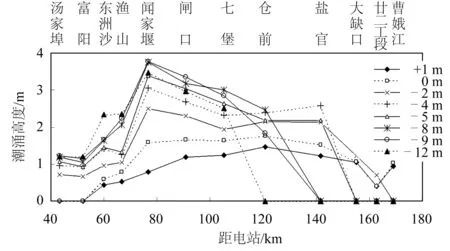
图11 不同地形下沿程涌潮高度Fig. 11 Tidal bore height variation along the river under different topographies
涌潮强度可用相对Froude数Fr来表征[14-15]。当1
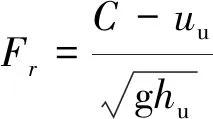
(12)
式中:hu为潮前水深,C为涌潮传播速度,uu为潮前流速。
将式(11)代入式(12),得
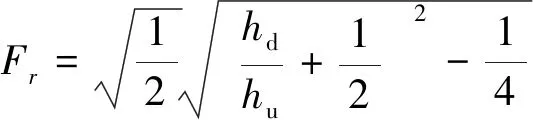
(13)
将hd=hu+ΔH代入式(13),得
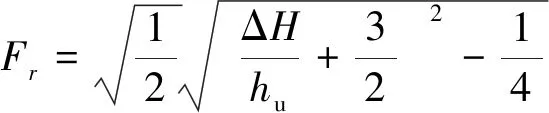
(14)
根据数模计算得到hu、ΔH,继而由式(14)计算出Fr列于表1。可见,不同地形下各站点Fr>1时,发生涌潮,涌潮高度与Fr密切相关,Fr越大,涌潮高度越大。
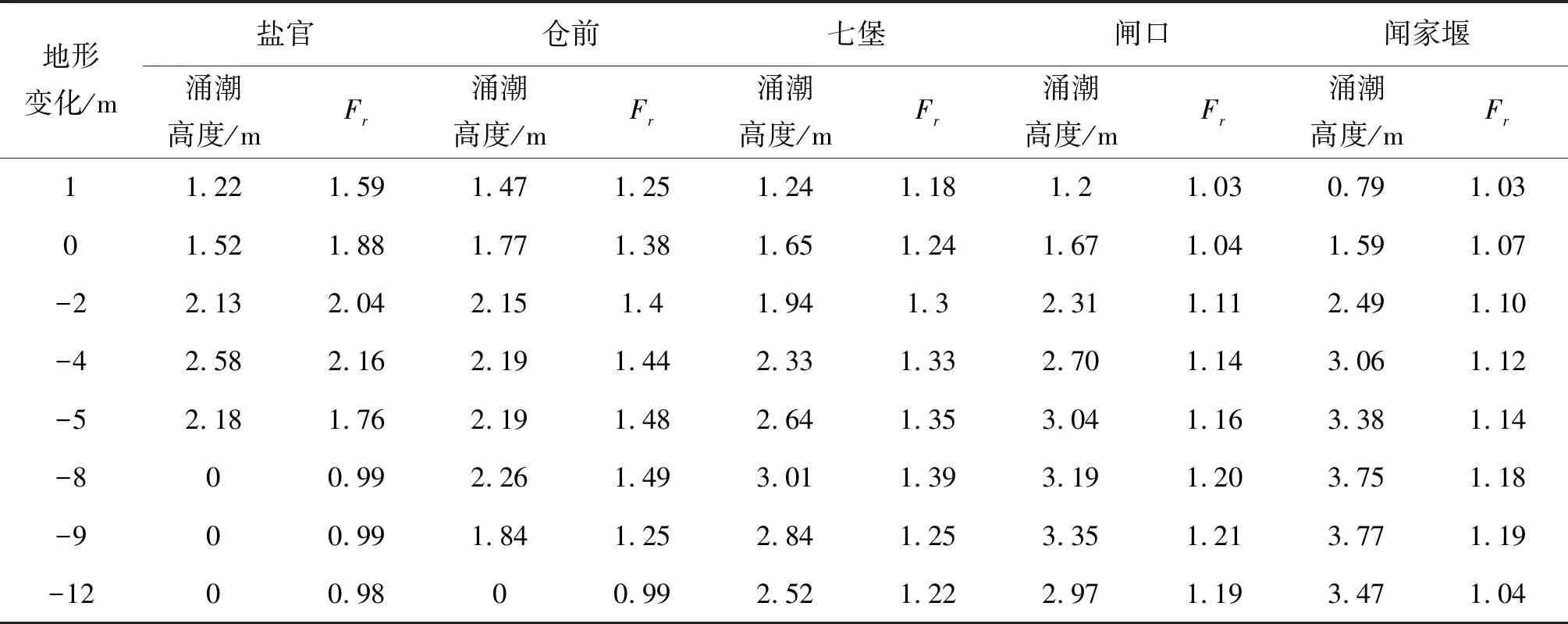
表1 各站涌潮高度与涌潮到达时的相对Froude数FrTab. 1 Height of tidal bore and relative Froude number when tidal bore appears at each station
4.2.2 涌潮起潮点变化
原地形时,涌潮起潮点位于曹娥江口以下(图11)。随着地形下降,起潮点向上游移动,涌潮总体也呈上移趋势。至地形下降12 m,起潮点移至七堡和仓前间。这一现象解释了在唐朝时富阳能看到涌潮,随着江道容积缩小,宋朝时移至六和塔,后经大规模治江缩窄,盐官至澉浦河段进一步淤积,强涌潮河段下移至盐官大缺口一带。
4.2.3 涌潮流速和传播速度变化
涌潮流速与涌潮高度、潮前(落潮)水深、潮前(落潮)流速相关[1]。根据数模计算,当地形降低时,涌潮流速增加,涌潮高度先增后减,潮前水深增大,潮前流速也增大,三个因素的联合作用致涌潮流速在某一地形下达到极值。如盐官站,在原地形下,涌潮流速最大;而在七堡,在地形降低4 m时,涌潮流速最大(图12)。
图13绘出了各地形下沿程涌潮传播速度。因下游水深小,涌潮传播速度下游小于上游。同一地点,地形降低,涌潮传播速度增加。
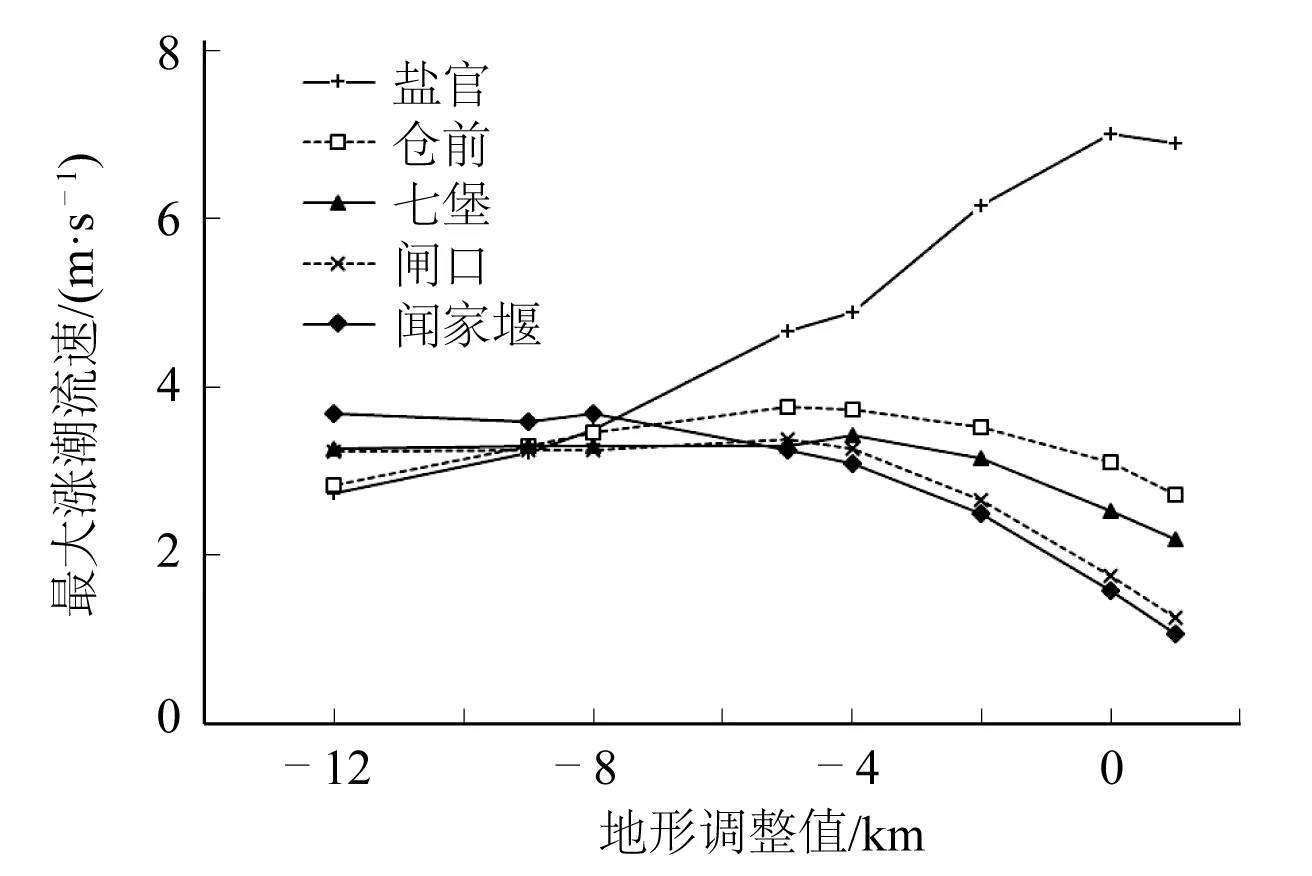
图12 不同地形下各站涌潮流速Fig. 12 Maximal velocity of the tidal bore under different topographies
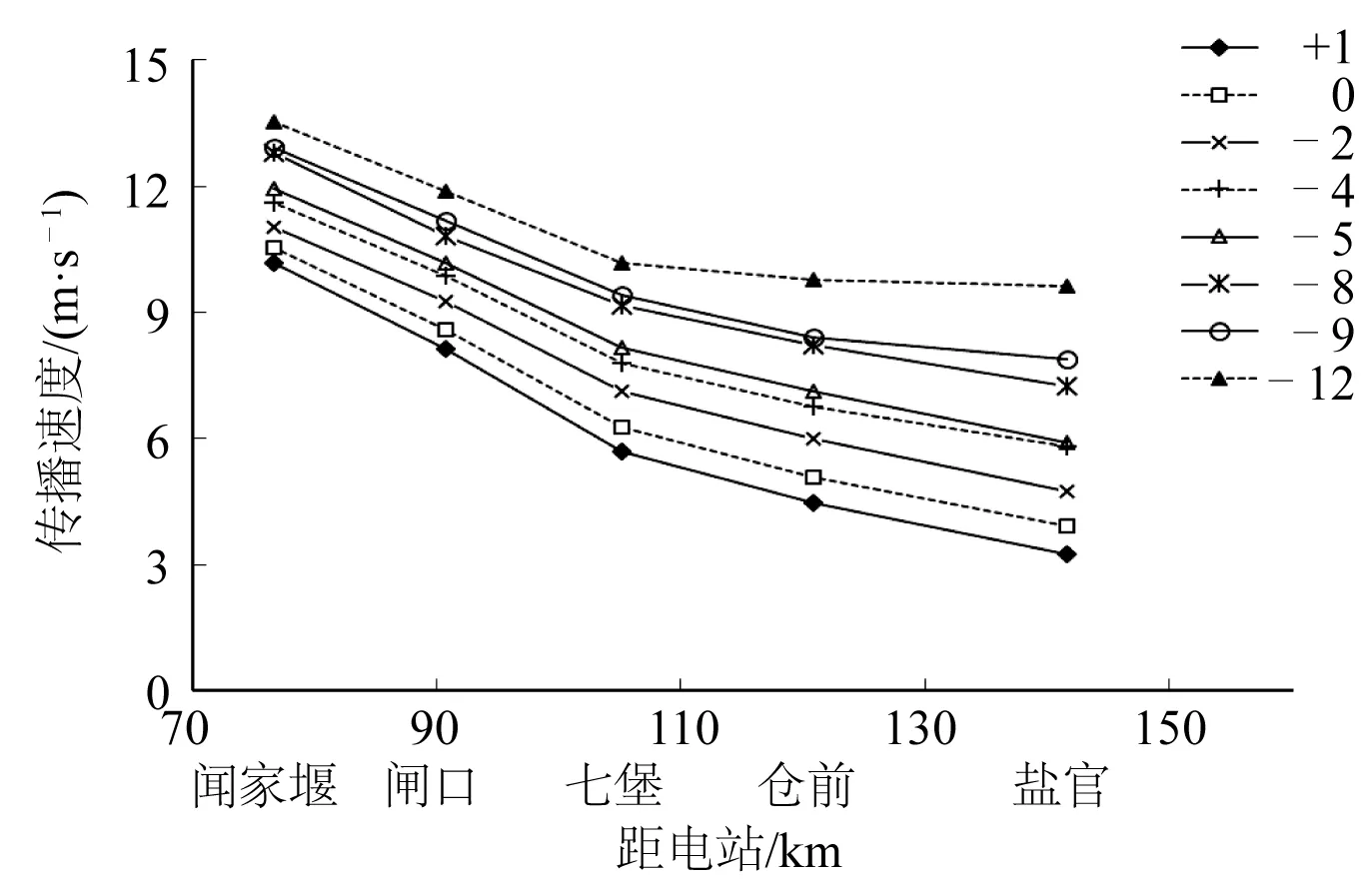
图13 不同地形下涌潮传播速度Fig. 13 Propagation speed of the tidal bore under different topographies
4.2.4 涌潮潮景变化
图14和图15绘出了涌潮到达盐官和老盐仓时的水位等值线。原地形时,盐官“一线潮”和老盐仓“回头潮”清晰可见。盐官潮前、潮后的水位分别为1.0 m和2.5 m,相对Froude数为1.88;当地形减低4 m时,“一线潮”和“回头潮”仍十分明显,盐官潮前、潮后的水位分别为-2.0 m和0.0 m,水位等值线更加密集,相对Froude数为2.16,水流漩滚进一步增大,涌潮更为壮观。当地形减低8 m时,相对Fr<1,涌潮潮景消失。
图14 盐官各地形下水位等值线Fig. 14 Water level contour at Yanguan reach under different topographies
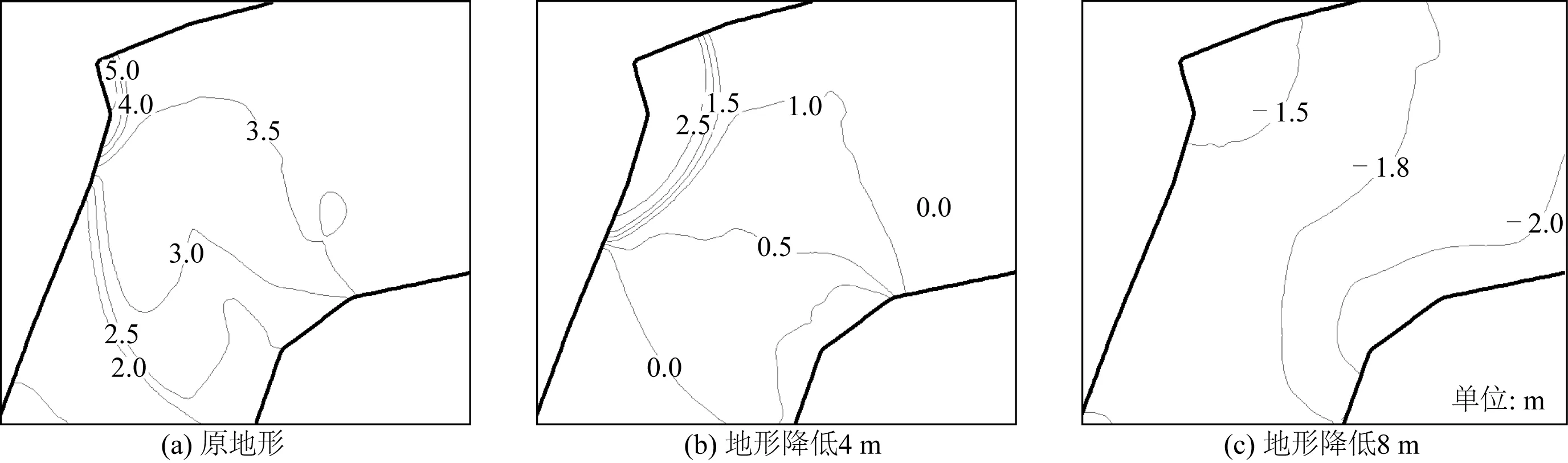
图15 老盐仓各地形下水位等值线Fig. 15 Water level contour at LaoYancang reach under different topographies
4.2.5 涌潮陡度变化
涌潮陡度为涌潮潮头高度与潮头长度的比值,是衡量涌潮强度的参数之一。考虑到计算网格较粗,直接计算涌潮陡度结果远远偏小,因此采用涌潮陡度计算公式[16]:
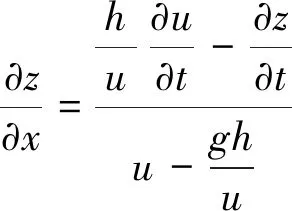
(15)
应用式(15)计算涌潮在盐官断面的陡度,尽管相比实际情况计算结果偏小[16],但从定性上仍能得到一些规律。图16为涌潮高度、相对Froude数、涌潮陡度的曲线,可见,涌潮陡度和涌潮高度、相对Froude数具有较好的相关性。当地形降低4 m时,盐官涌潮高度、相对Froude数最大,此时涌潮陡度也最大。
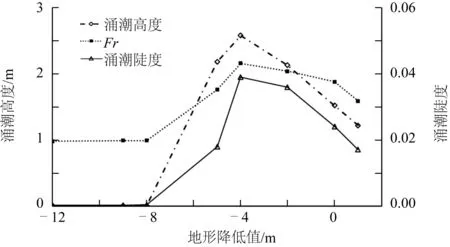
图16 不同地形下盐官涌潮陡度Fig. 16 Steepness of the tidal bore under different topographies at Yanguan
5 结 语
采用数学模型计算了8种地形条件下钱塘江涌潮特征的变化,得到以下结论:
1) 因钱塘江江道宽浅,地形对河口的潮汐影响大。随着地形降低,低潮位随之降低,高潮位以降低为主,潮差增大,涨潮历时增加,落潮历时缩短。
2) 地形对涌潮影响显著。随着地形降低,涌潮高度、涌潮最大流速先增后减,涌潮传播速度增加,起潮点上移。相对Froude数能较好地表征涌潮的形成和强弱,当地形降低致相对Fr<1时,涌潮消失。
3) 研究成果可解释钱塘江河口丰水江道下涌潮大、枯水江道下涌潮小的现象,说明了治江缩窄后因盐官至澉浦河段淤积造成江道容积减小,导致涌潮起潮点和强涌潮段下移的机理。为使涌潮具有较好的观赏性,防止江道过度淤积,动态维持适当的江道容积是必要的,这对钱塘江河口治理和涌潮保护具有重要的现实意义。
