基于局部时间步长方法的潮流数值模型研究及应用

胡 鹏，姬奥飞，陶俊余

(浙江大学 海洋学院，浙江 舟山 316021)

浅水方程被广泛用于模拟潮流过程[1-5]。在20世纪七八十年代，普莱斯曼(Preissmann)隐格式[6]因结构简单、无条件稳定以及对时间步长没有限制等优点，被广泛用于求解浅水方程[7]。夏云峰[8]采用SIMPLE、SIMPLEC和SIMPLER算法对动量方程和连续方程耦合求解。近年，基于压力分裂模式和θ半隐算法，并采用欧拉-拉格朗日方法(ELM)求解对流项的浅水模型，因其“无条件稳定”的特征而得到了关注[9]。浅水方程的解可能包含间断/激波[10-13]，表现为水跌或水跃、风暴潮、涌潮等。为捕捉这些现象，基于黎曼近似解通量的有限体积法被广泛应用[14-15]，此类模型时间步长受到约束，如CFL稳定条件[16]。当网格尺度或水流不均匀时，网格之间的最大允许时间步长可能相差很大。为程序编写方便，这类模型往往采用整体最小时间步长，将单元时间步长取为所有网格允许最大时间步长的全局最小值，这简化了程序编写，但限制了计算效率。为提高计算效率，局部时间步长(LTS)方法受到关注。相对于传统方法，LTS法使每个网格采用满足稳定性的尽可能大的时间步长[17-19]。然而，当最大和最小时间步长相差倍数太大时，二维浅水模型的LTS法可能存在不稳定性[19]。胡鹏等[16, 20]通过限制激波/间断处的时间步长空间梯度，得到了稳定的局部时间步长方法。在此基础上，建立高性能的平面二维潮流数值模型，以长江口、杭州湾和渤海、黄海、东海的潮流为例，验证其计算效率和精度。

1 数学模型

1.1 基于有限体积法的浅水模型

平面二维浅水方程可写成向量形式如下：

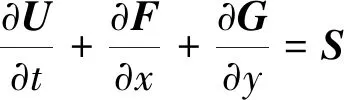
(1)

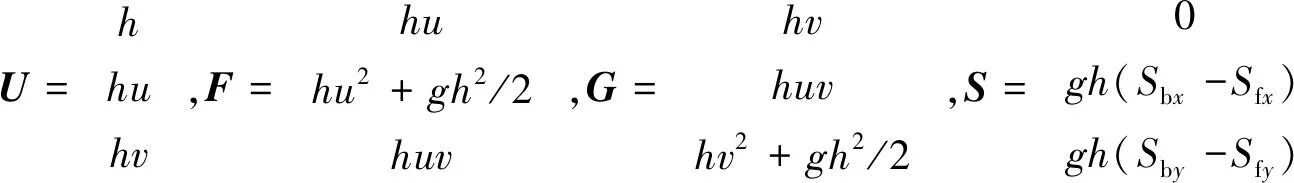
(2)

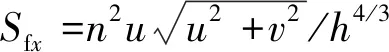
非结构三角形网格示意如图1所示。

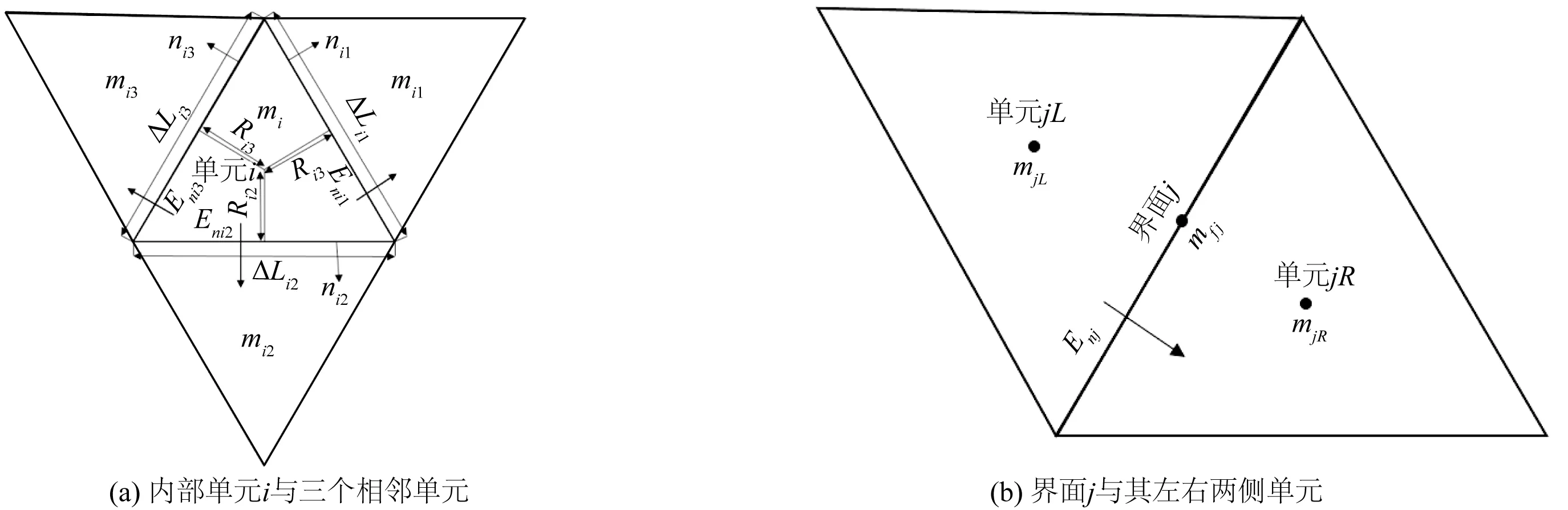
图1 非结构三角形网格示意Fig. 1 Sketches of the unstructured triangular meshes

图1(a)为计算区域内部某单元(编号为i，i=1,2,3,……,Nc；Nc为总单元数)以及三个相邻单元(编号分别记为：i1、i2、i3)；图1(b)为某个界面(编号为j，j=1,2,3,……,Nf；Nf为总界面数)及其左右两侧的单元(编号分别记为：jL、jR)。

针对单元i，采用有限体积法对控制方程(1)进行离散可得[21]：

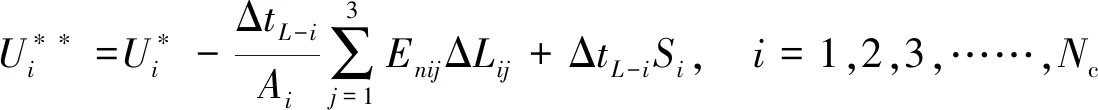
(3)

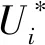
Enj=FHLLC(UjL,UjR)

(4)

其中，UjL和UjR分别为界面j两侧的黎曼状态；FHLLC为HLLC黎曼算子。调用HLLC黎曼算子之前，采用非负水深重构界面两侧的黎曼状态[24-25]。HLLC黎曼算子的具体表达式可参考文献[21]。

1.2 LTS方法及其实现过程

首先通过下式计算各单元允许的最大时间步长：

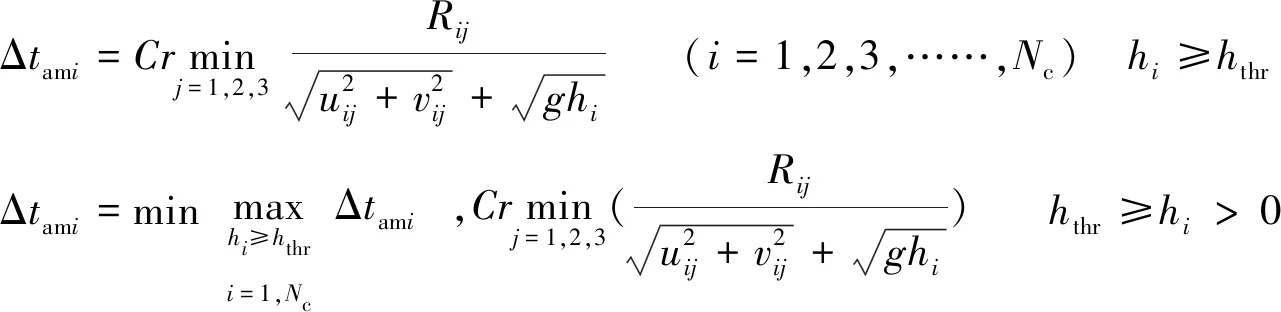
(5)

式中：Δtami为第i单元的最大允许时间步长；Cr为克朗数，设定为0.9；uij，vij为第i单元第j界面法向水流流速；hi为第i个单元的水深；Rij为单元中心到第j界面的距离；hthr=10-6m为临界水深。其次，计算整体最小时间步长Δtmin和各单元时间分级指数mi：

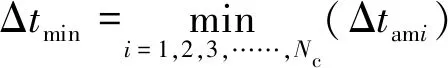
(6)

(7)

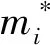
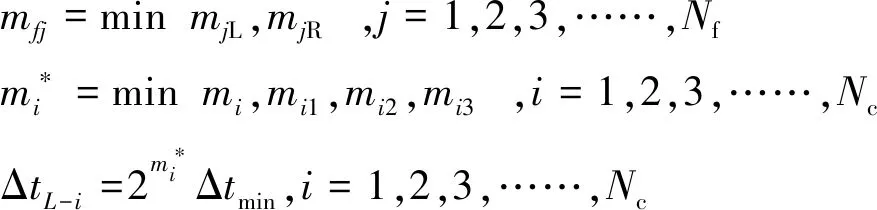
(8)

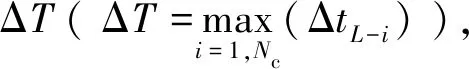
1) 计算界面数值通量时，如果特征值(np-1)/2mfj为整数，则计算，否则不更新。

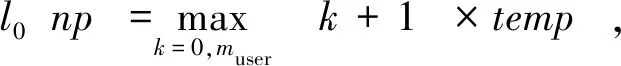
(9)

2 LTS方法对模拟结果的影响

采用L(f)量化LTS方法与传统整体最小时间步长方法之间的相对误差，这里L(f)描述的相对误差是指采用LTS法计算的某一变量值与采用整体最小时间步长方法计算出的这一变量值之间的相对差值，并对计算区域中所有节点的相对差值进行统计，最终得到一个面上的统计值。采用ε量化全局水体质量相对误差。L(f)及ε计算式为：

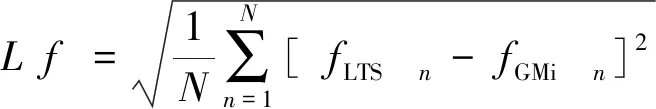
(10)

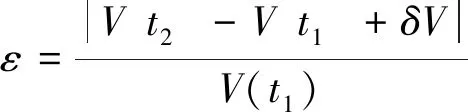
(11)

式中：参数f表示水动力变量，如水位、流速等；N为网格节点总数；fLTS和fGMi分别表示LTS方法和传统整体最小时间步长方法的计算结果；V(t1)和V(t2)表示计算区域在t1和t2两个时刻包含的水体总体积；δV表示在这两个时刻之间从边界净流入或流出的水体体积。

计算区域如图2所示。三角形网格总数为117 323，最小边长约180 m，最大边长约38 000 m。地形采用2016年2月实测地形资料(徐六泾—口门附近)和杭州湾、渤海、黄海、东海海图。长江径流边界取在三江营，采用大通流量过程作为边界条件。长江口潮流界在江阴以下，潮区界位于铜陵和芜湖间[26]。因此，三江营不受潮流影响。钱塘江给流量800 m3/s。外海开边界位于大陆架内侧，为水位驱动，考虑M2等13个分潮，通过海潮模型TPXO计算。初始水位、流速设为0；各单元的糙率采用公式0.01+0.01/h计算[27]。

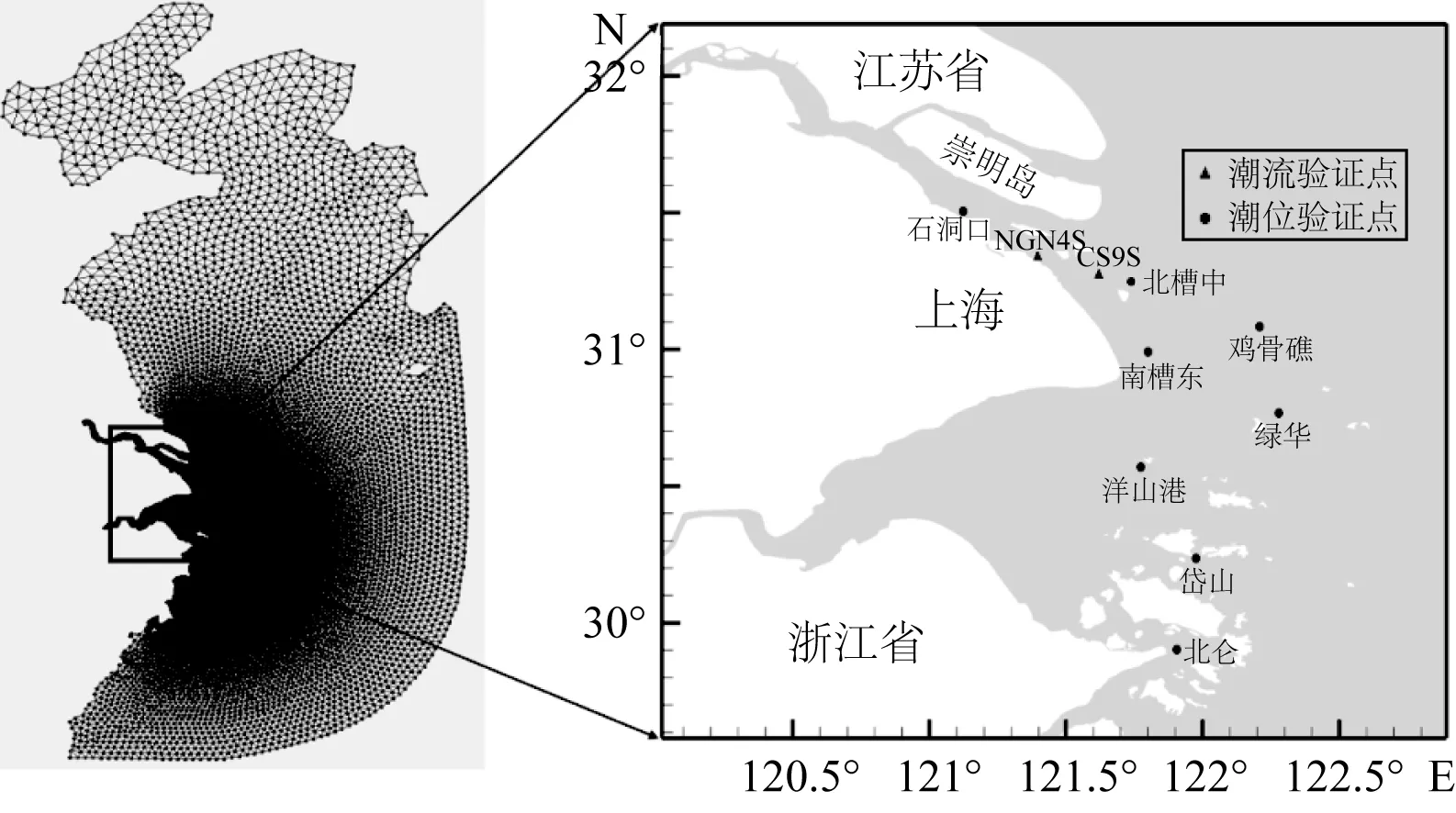
图2 计算区域、非结构网格和实测数据站点位置Fig. 2 Computational domain, unstructured grids and stations for measuring data

模拟2016年7月10日至7月13日的潮流过程，考虑muser取值从1到7共7个LTS方法工况，与传统整体最小时间步长方法对比(即取muser=0)。表1是两种方法计算效率和相对误差的对比。由表1可知：1) LTS方法能大幅度提高模型计算效率。模型计算耗时随着muser的增加而降低。传统方法计算耗时12.75 h，而LTS法(取muser=7)仅耗时1.77 h，LTS方法的计算效率提高约7.2倍。2) LTS方法带来的相对误差可以忽略，远小于传统方法与实测数据之间的相对误差。虽然LTS方法带来的相对误差随着muser增大略有增加，但最大仅为12 mm(水位)、0.66 mm/s(流速)，远小于传统方法与实测数据之间的相对误差：179 mm(水位)，186 mm/s(流速)。3) 基于LTS方法的潮流模型具有满意的守恒性。采用式(11)计算全局水体质量相对误差ε，其数值越接近0说明计算格式守恒性越高。结果显示，基于LTS法的有限体积法(muser=7)的全局水体质量相对误差ε仅为10-12，表明模型的守恒性令人满意。

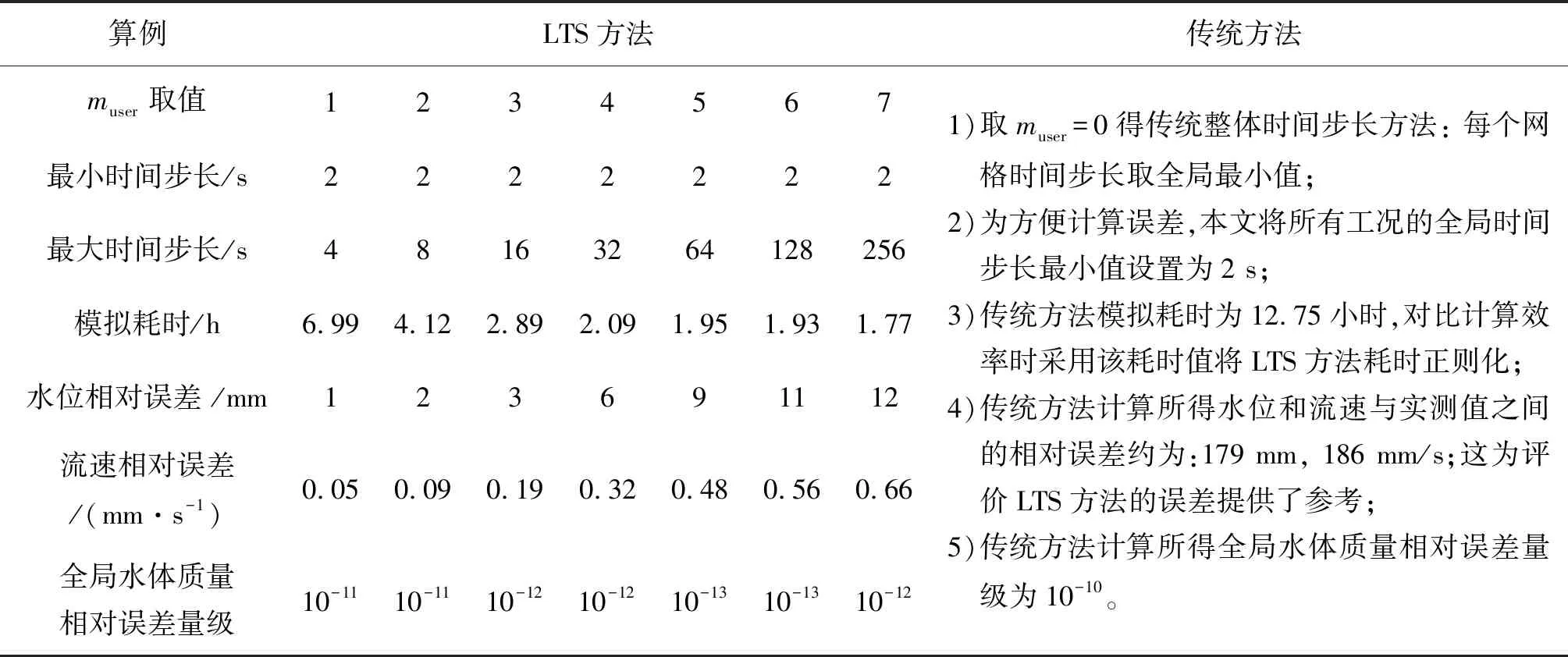
表1 LTS方法与传统方法之间的对比Tab. 1 Comparison between LTS approach and traditional method

3 模式在长江口、杭州湾及渤海、黄海、东海的应用

3.1 渤海、黄海、东海潮汐特征

图3为计算所得M2分潮在渤海、黄海、东海的同潮图，包括潮差分布(图3(a))和迟角分布(图3(b))。从图可以看出，潮波从外海边界传入后，向西北和西南两个方向传播。向西北方向传播的潮波，首先在渤海、黄海分别形成两个逆时针旋转的潮波系统，两个中心点分别在(34°50′N，120°35′E)和(37°59′N，122°50′E)附近；之后潮波继续向北，经渤海海峡后再次分成两个方向，部分沿渤海海峡方向向西传播，另一部分右转向北传播，再次形成两个逆时针旋转的渤海半日潮波系统，其中心点分别在(38°26′N，119°5′E)和(40°15′N，120°48′ E)附近。上述结果与张衡等[28]所述的潮波传播特征基本一致。如图3(a)，M2分潮最大振幅约为3.14 m，位置在朝鲜半岛西部的江华湾附近(图3(a)中黑色圆点所示)。朱学明等[29]基于FVCOM海洋数值模式模拟了渤海、黄海、东海的潮汐、潮流，认为江华湾顶M2分潮最大振幅达3.2 m，支持了本文模拟结果。黄海区域和渤海区域分别存在两个振幅接近于0的点，即无潮点，如图3(a)黑色三角形所示，与沈育疆[30]所得无潮点位置(图3(a)黑色五角星)接近。对比图3(a)和图3(b)还可看出，无潮点周围对应一个逆时针旋转的潮波系统；无潮点周围分潮振幅等值线与迟角等值线大致垂直。

图3 M2分潮同潮图Fig. 3 The distribution of coamplitude and cophase of the M2 tide constituent

3.2 潮位与潮流验证

根据可得实测数据，验证长江口四个测站(石洞口、鸡骨礁、南槽东、北槽中)的潮位(图4，2016年7月10日至8月10日)，两个测站的流速和流向(图5，2016年7月21日至月22日)；杭州湾四个测站(洋山港、北仑、岱山、绿华)的潮位(图6，2015年6月29日至7月9日)。测站位置如图2所示。从图4～图6可以看出，潮位、潮流(流速和流向)的模拟值与实测值吻合良好。

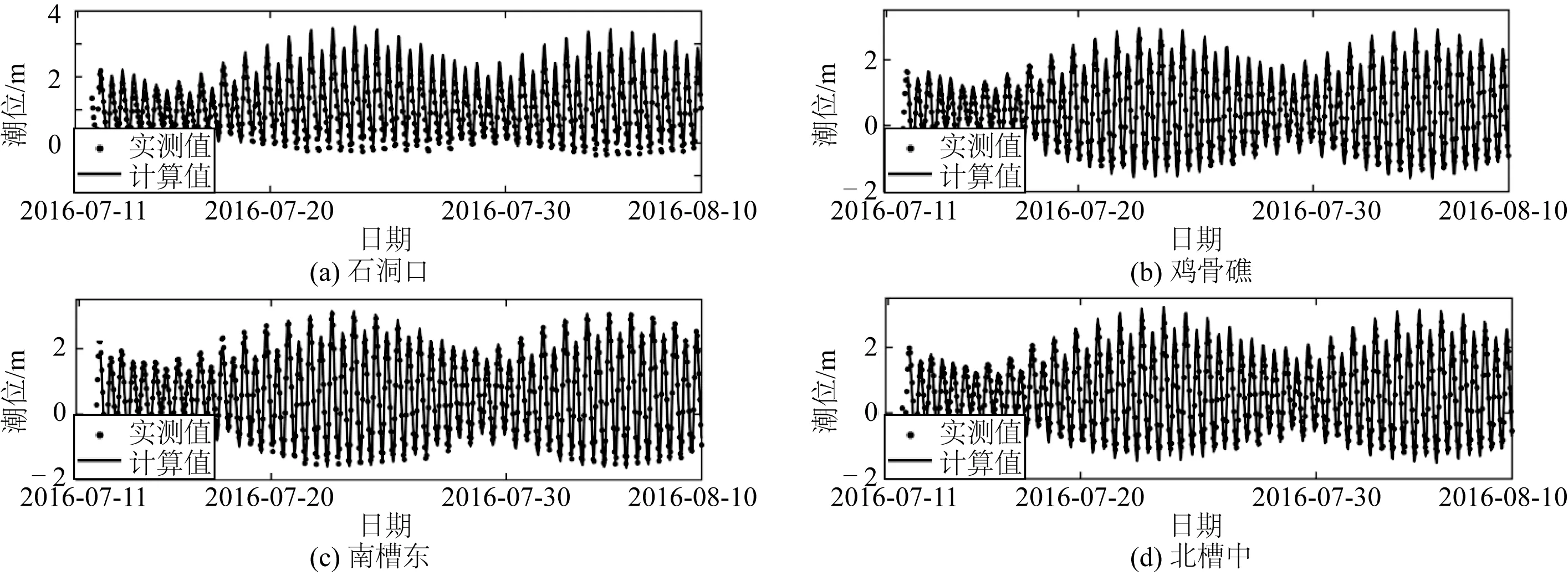
图4 长江口计算水位与观测值比较Fig. 4 Comparison of calculated and observed water levels in the Yangtze River estuary

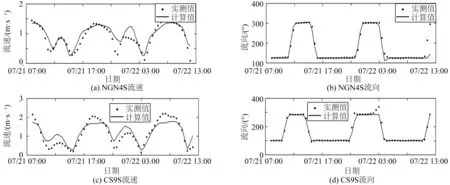
图5 垂向平均流速和流向验证Fig. 5 Validation of vertical average current speed and direction

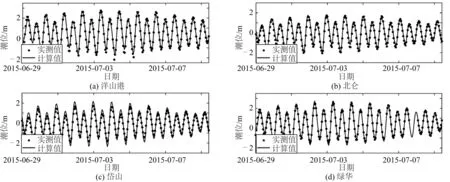
图6 杭州湾计算水位与观测值比较Fig. 6 Comparison of calculated and observed water levels in Hangzhou Bay

采用均方根误差RMSE、相关系数CC和技术评分SS等参数进一步量化误差，计算式如下

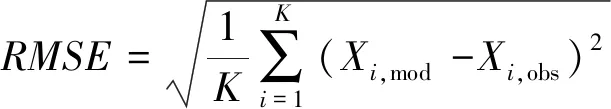
(12)

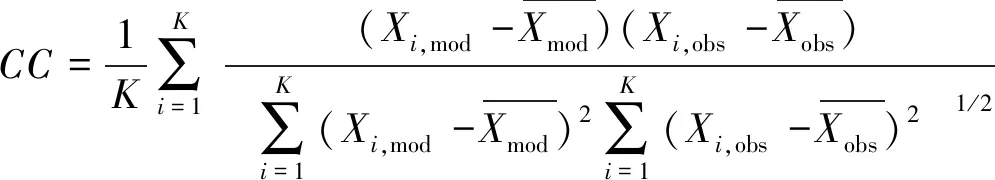
(13)

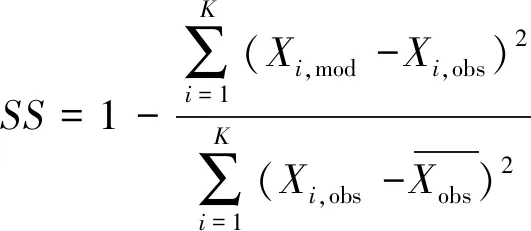
(14)

误差统计结果如表2所示。潮位计算值与实测值之间的均方根误差范围在0.179 m到0.362 m之间(绿华站最小，石洞口站最大)。考虑到最大潮差约为4.5 m(洋山港)，这样的潮位误差可接受。流速、流向的均方根误差范围在0.186 m/s到0.287 m/s之间(NGN4S站最小，CS9S站最大)和13°37′到24°4′之间(CS9S站最小，NGN4S站最大)。考虑到最大流速约为2.2 m/s(CS9S站)，流向最大变化范围约为180°，模型计算的流速、流向误差也可接受。相关系数CC和技术评分SS，分别在0.9以上和0.76以上，表明模型计算值与实测值吻合程度很好[31]。

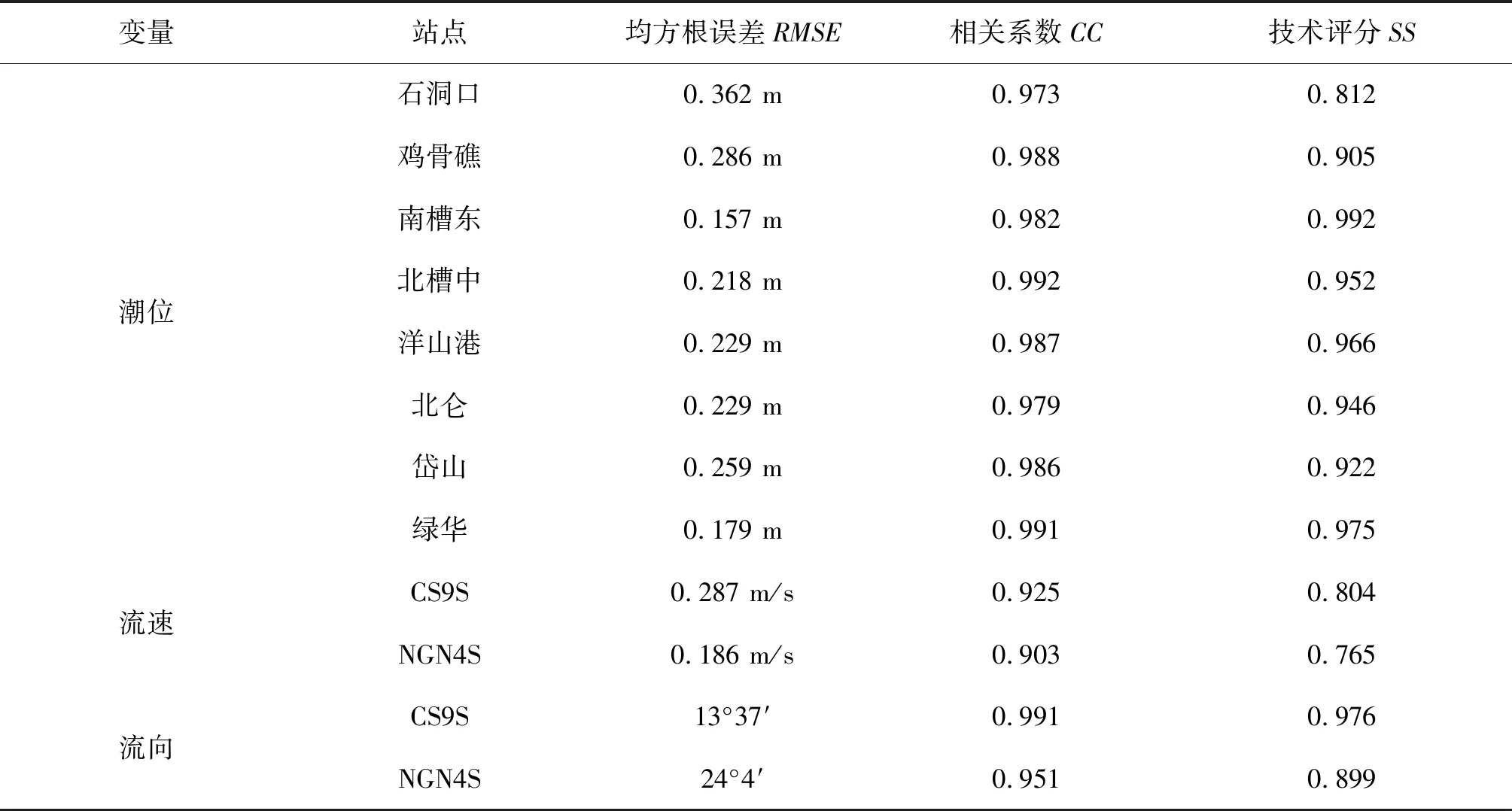
表2 误差分析Tab. 2 Error analysis

4 结 语

建立了基于LTS方法的平面二维潮流数值模型。模型采用非结构三角形网格，对局部区域加密，通过LTS方法提高模型计算效率。对比表明，LTS方法和传统整体最小时间步长方法两者之间的水位、流速、流向相对误差均较小，但LTS法可使模型计算效率大幅度提高(本文工况计算效率提高了约7.2倍)。模型全局水体质量相对误差，在muser=7时仅为10-12，表明模型计算格式的守恒性也较高。最后，采用所建立的高效率平面二维模型，成功模拟了长江口、杭州湾、渤海、黄海、东海的潮流过程，计算所得潮流传播特征、振幅分布、无潮点均与前人结果相符，与长江口、杭州湾十余个站点实测数据吻合良好。需要说明的是：LTS方法提高模型效率的具体倍数会随网格和流速非均匀性变化，在非常理想的情况下，即网格和流速都很均匀时，LTS的加速效果将减弱。实际上，网格局部加密非常普遍，实际水流往往也是非均匀的，文中模型在大多具体实例中的加速效果将是显著的。