海堤坡角变化对海啸波传播过程影响数值分析

翟钢军，鲍建宇，马 哲，孙家文，赵西增

(1. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024; 2. 大连理工大学 深海工程研究中心，辽宁 大连 116024; 3. 国家海洋环境监测中心 海域管理技术重点实验室，辽宁 大连 116023; 4. 浙江大学 海洋学院，浙江 舟山 316021)

海啸作为全球最具破坏性的灾难之一，不仅会造成大量的人员伤亡，还会导致近岸结构物的严重破坏，造成财产上的巨大损失。而海堤作为重要的防波堤工程，在近海海域得到了广泛的应用[1]。陈杰等研究了海堤破碎区至冲泻区的水动力特性[2]，此外还关注了海啸波作用下的泥沙运动[3]。海啸波具有巨大的破坏性和强非线性，如何精准地模拟海啸波与海堤等结构物的相互作用，成为了水动力学领域学者们的研究热点。

目前，基于解析解和物理模型试验的研究方法已相对成熟，如房克照等[4]建立了基于高阶Boussinesq水波方程的波浪传播数值模型，可以有效处理波浪自由面间断流动的问题；任冰等[5]开展物理模型试验，研究了规则波在岛礁地形上的传播变化；赵西增等[6]开展了溃坝波与海堤相互作用的模型试验，高速相机能够较好地捕捉到自由面大变形现象。

在数值模拟方法的研究方面，郭立栋等[7]基于BEM与VOF波浪耦合模型开展了斜坡堤越浪研究，只用VOF模型很难模拟不规则波面的非线性流动；王东旭等[8]基于OpenFOAM网格法程序，数值模拟了孤立波在潜礁上的全传播过程，但缺少了对液面湍动变形处的细节模拟。可以看出，在模拟波浪局部液面大变形方面，传统的网格法(如FDM、VOF法等)仍存在模拟精度不高的问题，液面局部剧烈变形会使网格发生畸变、扭曲，一定程度上降低该方法的精度[9]，与其他数值方法耦合或网格的局部加密进一步增加了数值计算的难度。

近年来，相关学者在采用溃坝波近似模拟海啸波的研究中取得了一系列成果。Chanson等[10]通过解析解公式推导和自由波面拟合，验证了溃坝波与海啸波涌潮在传播过程中存在着相似性。此外，由于溃坝波物理模型试验的可重复性高，技术条件成熟，随后越来越多的学者开展了基于溃坝波模拟海啸波的研究。如Mcgovern等[11]基于SPH法模拟了海啸波的越浪和爬升过程；Wei等[12]基于SPH法利用溃坝波模拟海啸波，研究了海啸波与桥墩的相互作用问题；赵西增等[6]建立溃坝波试验模型模拟海啸涌浪；张学莹等[13]应用SPH法对二维和三维溃坝波与结构物相互作用过程进行了模拟分析；陈橙等[14]基于溃坝波机制模拟海啸波冲击码头的模型试验。SPH法作为新兴的无网格粒子法，在提高自由液面大变形计算精度方面取得了长足进展。SPH粒子具有自适应性，流体粒子包含速度、压强、位置等全部信息，无需计算对流项和输运项，从而消除了自由界面上的数值耗散，这使得SPH法能够清晰准确地追踪自由液面。总结以上研究成果，下文进一步关注不同海堤坡角情况下，SPH法边界条件对数值求解结果的影响。

在SPH数值模型中采用溃坝波数值模型，基于赵西增等开展的溃坝波物理模型试验数据展开对比验证。溃坝波的波高与下游水深比值接近于1.64时达到了波浪强非线性条件。通过建立溃坝波数值模型，对比试验室中溃坝波冲击海堤的物理模型试验结果，精准地再现了海啸波的传播过程，同时再现了堤前液面大变形和堤后射流、崩破波的出现与演变过程。海堤坡角改变时，传统网格法需进行不同的网格局部加密处理，这里基于无网格法的独特优势，利用SPH法数值模拟方法研究了坡角对波浪爬高与衰减以及消波系数的影响。

1 理论基础及边界条件的建立

SPH法是一种无网格粒子法，用一系列任意分布的粒子来离散问题域，通过核函数积分进行估值近似，一般采用显式格式对离散的线性方程组进行时间积分[15]，采用标准蛙跳(leapfrog)法，使时间步长Δt满足CFL条件，保证数值求解结果的收敛性。SPH法中构造的光滑函数在支持域上要满足正则化条件和紧支性条件，同时要保证其对称性和光滑性。SPH数值模型基于开源数值程序SPHERAv.8.0 (RSE SpA)建立[16]，目前常用核函数有B样条核函数、高斯型核函数、三次样条核函数等，下文采用B样条核函数进行模拟。

1.1 基本原理

在SPH方法中，函数f(x)的积分表达式：

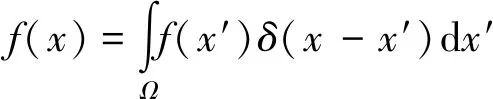
(1)

若函数f(x)在积分域Ω内连续，可以用光滑函数W(x-x′,h)来代替，此时方程f(x)的积分表达式可写为：

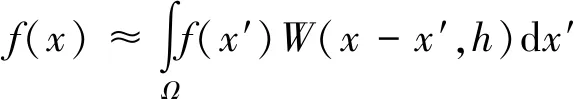
(2)

式中：f(x)是三维坐标向量x的函数，Ω为包含x的积分域，即粒子法的整个求解域，δ(x-x′)为狄拉克δ函数，W(x-x′,h)为核函数，(x-x′)为粒子间距，h为光滑长度。

1.2 求解N-S方程

拉格朗日形式下流体的连续性方程：

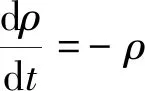
(3)

简化后的动量方程：

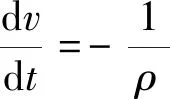
(4)

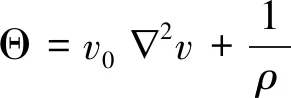
(5)

式中：P为粒子压力，ρ为流体粒子密度，t为时间，g为重力加速度，v为粒子运动速度，Θ为紊动项，v0为水的运动黏性系数，τ为应力张量。

1.3 建立固边界条件

固边界的设置直接决定了边界附近流场的稳定性和计算域的计算精度，一直以来确定合适的边界条件都是SPH法的研究热点与难点，主要研究的三种固边界处理方法如图1所示。镜像粒子法最早提出，能够改善SPH法的边界缺陷，但每一时间步生成相当数量的镜像粒子，极大地增加了计算负担。边界排斥力法将固边界用一系列的粒子来模拟，对靠近固边界的流体粒子施加作用力，防止流体粒子穿透边界，但在处理不规则的边界条件时边界力易出现叠加扰动，破坏守恒条件。而海堤坡角改变时，边界力的形式、大小及方向都会随之改变，这两种边界处理条件都会引起初始扰动，破坏守恒条件。

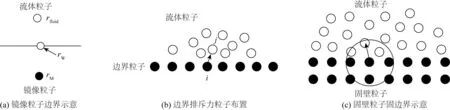
图1 三种固边界处理方法Fig. 1 Three methods of solid boundary treatment

固壁粒子法设置简单，适用于复杂几何固边界问题，不受作用力大小及方向的限制，文中不同坡角的海堤前坡边界条件即采用固壁粒子法处理。其中，位于边界附近的流体粒子i受到边界粒子k的作用力计算如下，pi是流体粒子的压力，pk是固边界粒子的压力，初始排斥力如式(6)计算。

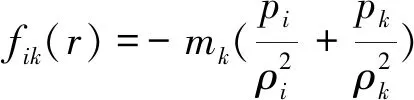
(6)

基于半解析法边界条件，对初始作用力求一阶偏导，利用粒子的自适应性迭代求解各个时刻的边界排斥力及压强：

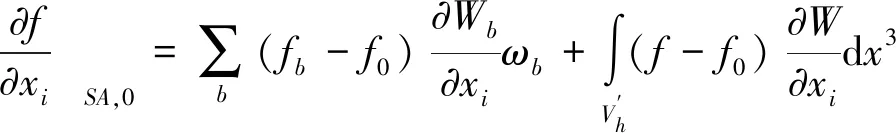
(7)

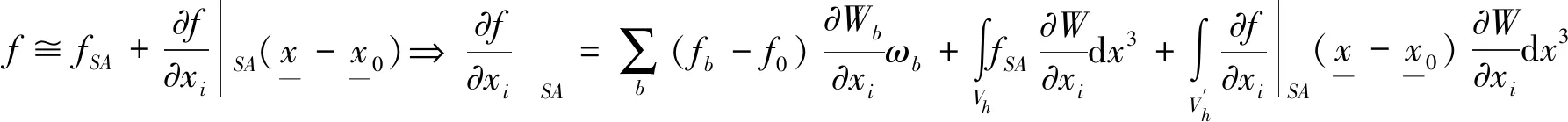
(8)

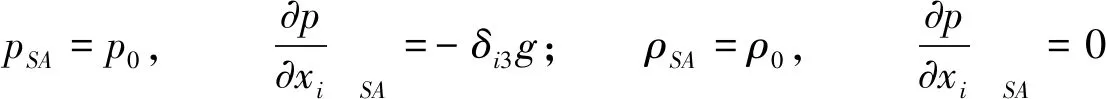
(9)

此时，基于半解析固壁粒子边界条件的SPH连续性方程推导为式(10)所示，其中Cs为流固耦合项。

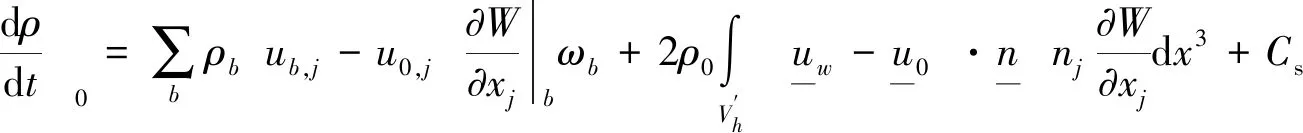
(10)

该边界条件保证了流体粒子不能穿越固边界，基于Monaco等[17]提出的半解析边界处理方法，在连续性方程中引入流固耦合项，设置为无滑移边界条件，符合真实流体在水槽中的运动情况。

2 粒子间距敏感度及波面分析

数值模型水槽尺寸为600 cm×40 cm×60 cm(长×宽×高)，通过挡板将水槽分为长200 cm的蓄水段和长400 cm的试验段。防波堤模型为斜坡式，下底长45 cm，上底长20 cm，高11 cm，前端距闸门128 cm。上游初始水深20 cm，下游初始水深为与防波堤等高，h=11 cm，试验布置如图2所示。

数值模型参考物理模型试验布置，物理模型试验数据参考文献[6]。

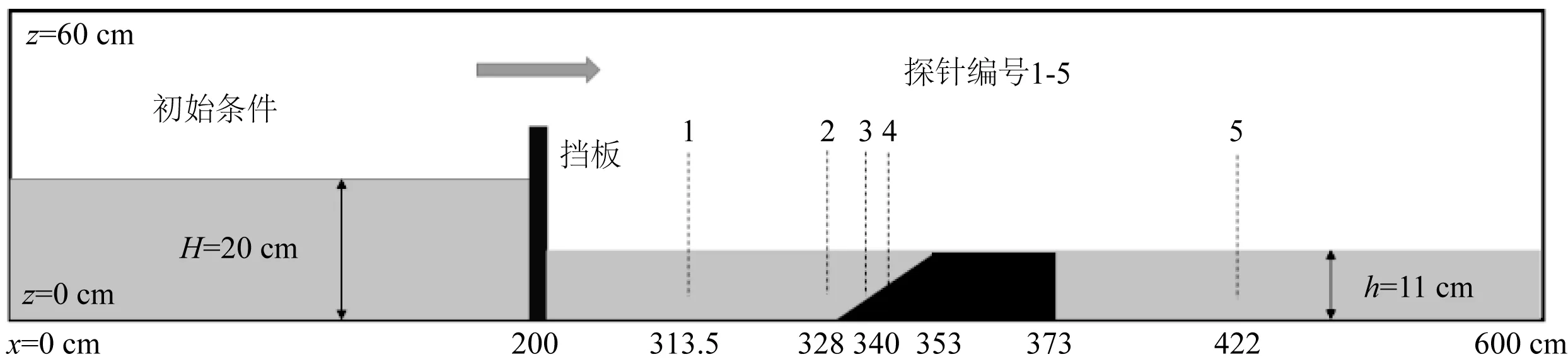
图2 模型试验布置示意Fig. 2 Layout drawing of model experiment

2.1 粒子间距敏感度分析

本节设置三组数值模拟算例，讨论SPH法粒子初始间距对于模拟精度的影响。粒子初始间距分别设置为0.002 m、0.005 m和0.010 m，对应的粒子数分别为203 015个、32 171个、8 043个。通过分析对比模拟结果发现，采用0.010 m的粒子间距时，由于粒子间距过大，初始粒子数量过少，数值模拟已无法形成具有清晰轮廓的自由液面图，故此粒子间距设置不予采纳。

数据处理时采用无量纲坐标(x/H,y/H)表示横、纵坐标，其中H为上游初始水深，取0.20 m。试验模拟结果和SPH法数值模拟波面对比如图3所示，其中t0时刻代表试验过程中水头靠近试验标记点(x=2.72 m,z=0.11 m)且标记点处液位上升1 cm时刻，经试验记录结果确定，时刻t0为0.56 s。图中圆点代表试验数据，海堤边界范围用黑线所画区域表示。

在t0+0.56 s时刻，海堤模型上底前端液位开始升高，液体即将进入海堤顶部；在t0+0.85 s时刻，水头前端运动到海堤顶部右端，此时水头前端面变形明显，涌水即将越过海堤右端，随即越过海堤形成射流，波面演变示意图如图3所示。

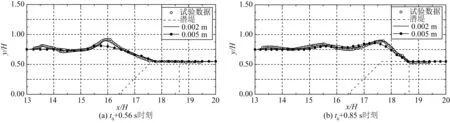
图3 试验与数值模拟波面结果对比Fig. 3 Comparison of wavefront change between experiment and numerical simulation

由数值模拟结果与试验数据的对比发现，数值模型粒子间距设置为0.002 m时，能更好地拟合液面流态的剧烈变化；粒子间距设置为0.005 m时，在溃坝波液面峰值处出现拟合误差，未能达到较高的模拟精度。由波面结果对比图可以看出，粒子间距设置为0.002 m时，数值模拟与试验数据的拟合精度最高，数值模拟7 s海啸波传播过程在计算机上需要运行10 h左右，计算成本可接受。在综合考虑模拟精度和计算成本后，文中数值模拟采用的粒子间距均为0.002 m。

2.2 海啸波传播过程波面分析

通过对比数值模型与试验中海啸波越堤前后的波面形态，分析海啸波传播的波面演变过程，捕捉海啸波与海堤相互作用时出现的一系列非线性现象。数值模拟结果如4左图所示，高速相机所拍试验照片如4右图所示，自上至下分别为t0时刻、t0+0.4 s时刻、t0+0.8 s时刻及t0+1.2 s时刻，试验及数值模拟海啸波翻越海堤过程的波面对比如图4所示。

图4 海啸波翻越海堤过程的数值模拟及试验对比图(试验照片引自文献[6])Fig. 4 Comparison of numerical and experimental result during the tsunami wave propagation (from reference [6])

分析试验数据图像可知，自t0时刻起，溃坝波开始进入高速相机的拍摄范围内，如图4(a)所示；t0+0.4 s时刻，溃坝涌水峰值开始接近海堤，波峰模拟现象明显，海堤模型上底前端液位将逐渐升高，涌水将进入海堤顶部，如图4(b)所示；t0+0.8 s时刻，相对平缓的溃坝水头前端逐渐升高并变得陡峭，波浪运动至海堤顶部距前端约1/3距离处，如图4(c)所示；随后溃坝波沿着海堤顶部继续向下游运动，在t0+1.1 s时刻越过海堤顶部下游顶点形成射流，如图4(d)所示，在形成射流初期，下游近海堤处出现了明显的液面凹陷，在重力的作用下，凹陷处上部流体随后闭合，产生了小范围内的崩破波流态。

通过采用物理模型试验与数值模拟相结合的方法，开展了上述溃坝波模拟海啸波与海堤相互作用的研究工作。研究结果表明，SPH法数值模型不仅可以完整地再现海啸波翻越海堤的全过程，而且能够准确地捕获非线性的自由面大变形现象，验证了SPH法数值模型的可靠性和准确性。

3 坡角角度对于海啸波传播的影响分析

《海港水文规范JTS 145-2-2013》中给出了斜坡堤无防浪墙的越浪计算公式：

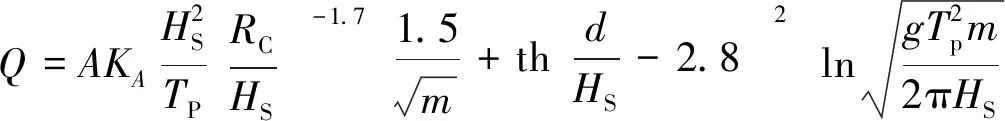
(11)

式中：Q为单位时间单位堤顶宽度的越浪量，m为海堤前坡坡度的余切值。由式(11)可以看出，在入射波浪有效波高HS、谱峰周期Tp、海堤堤脚处水深d等波浪参数一致时，海堤前坡度也是越浪量大小的决定因素之一，本节主要讨论海堤坡角对海啸波消波效果的影响。

3.1 波浪爬高分析

为保证波浪要素输入条件的一致性，数值模拟中统一设置上游溃坝水深为0.2 m，下游水深为0.11 m，在保证海堤堤顶高程相同的前提下，对比建立了7组不同坡角的算例，讨论海堤坡角对消波效果的影响。《防波堤设计与施工规范JTS 154-2018》中规定了不同护面型式下最小坡角与最大坡角分别为33.7°及51.3°。本文根据工程规范与斜坡堤铺设的实际需求，在规定坡角范围内做加密处理，选取坡角增量为5°，将坡角分别设置为20°、30°、35°、40°、45°、50°和60°，其中将20°和60°极限坡角作为对比参考值，共计算对比7组不同坡角情况，比较坡角选取范围的合理性和适用性，模型设置如图5所示。

图5 不同坡角海堤结构模型局部设置示意Fig. 5 Local layout of submerged breakwater models at different slope angles

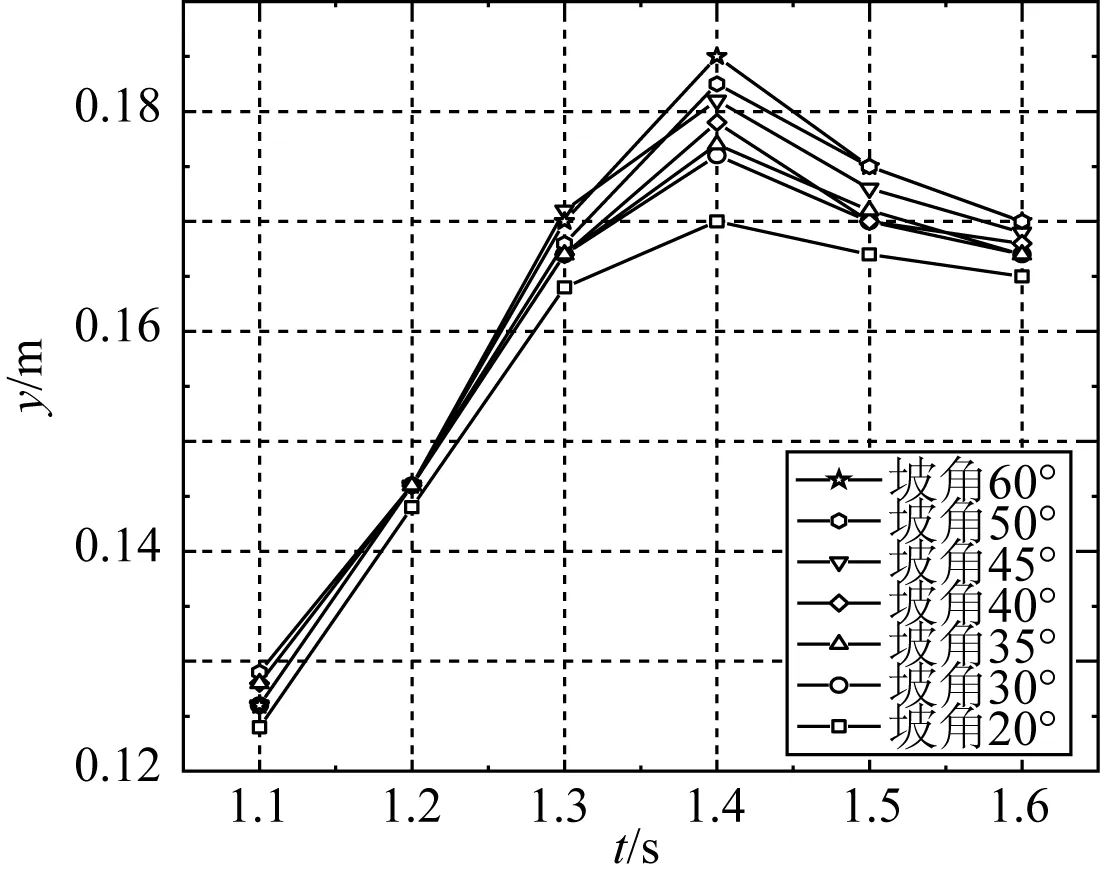
图6 x=3.450 m处波浪爬高变化曲线局部放大图Fig. 6 Partial enlarged detail of changing curve during the wave run-up at x=3.450 m

在海堤前x=3.450 m处设置探针，如图6所示为探针监测到的水位变化历时曲线局部放大图。从初始时刻开始，液面随着海啸波来浪而升高，在t=1.40 s时刻出现最大峰值水位；在t>1.40 s后，由于斜坡面波浪反射的影响，有效越浪量逐渐减少，探针处监测的液面高度也将持续下降。为了分析海堤前波浪爬高现象，获得探针位置处不同坡角下的液面抬升情况，波浪爬高量通过对比堤前水深h=0.110 m得到，整理坡角角度、波浪爬高峰值和峰值增长率的对应关系如表1所示。

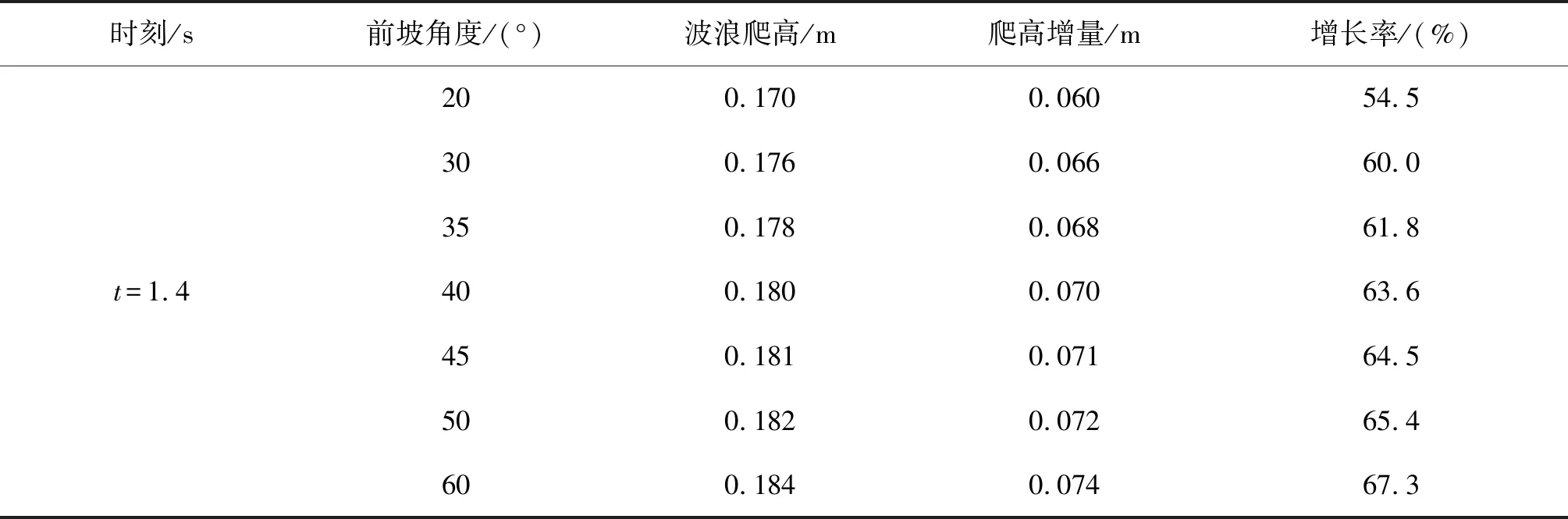
表1 波浪爬高增长率Tab. 1 Growth rate of wave run-up

由监测图像可以看出，坡角对爬高峰值的大小影响显著，随着坡角的增大，波浪爬高峰值增大，经由海堤斜坡边界造成的波浪反射不断增加。由于波浪爬高的大小会对堤后越浪有着显著的影响，进一步对比了波浪爬高的增长率，统计了平均爬高峰值增长率如表1所示。由表1可知，当坡角增量为5°时，随着坡角的增大，爬高峰值不断提升，增长率随之增大，爬高峰值受坡角变化的影响明显，坡角是影响波浪爬高和波浪反射大小的主导性因素。

3.2 堤后波浪衰减分析

随后探讨波浪越过海堤后的液面变化情况，这将作为海堤消波性能是否良好的重要指标之一。数值水槽长6 m，液面监测探针2设置在x=4.22 m处，故不考虑波浪在水槽右侧的反射问题，峰值在t=2.0 s时刻附近出现，通过不同角度海堤的消波系数对比，分析坡角变化对堤后波浪衰减的影响。

由表2中不同坡角海堤的波浪峰值对比可以看出，坡角对堤后波浪衰减影响显著，随着坡角的增大，堤后监测点处波浪峰值减小，波浪在越堤后传播时出现了明显的衰减现象。在规定的坡角范围内，当坡角增量为5°时，随着坡角的增大，峰值差值不断增大，消波系数随之增大。进一步分析图7中不同角度海堤消波系数变化对比图，在20°～40°小坡角范围内，增加坡角对提升消波效果作用明显，此时坡角是影响消波效果的主导因素之一；在40°～45°范围内，随着坡角的增加，消波系数达到0.18左右，此时增长缓慢；在45°～60°大坡角范围内，消波系数小幅提高，对消波效果提升有限。但考虑到大坡角情况下抛石斜坡堤的施工难度，此时不应超出规范坡角范围，而要优化海堤的堤顶宽度、超高等其他因素，进一步增强消波效果。

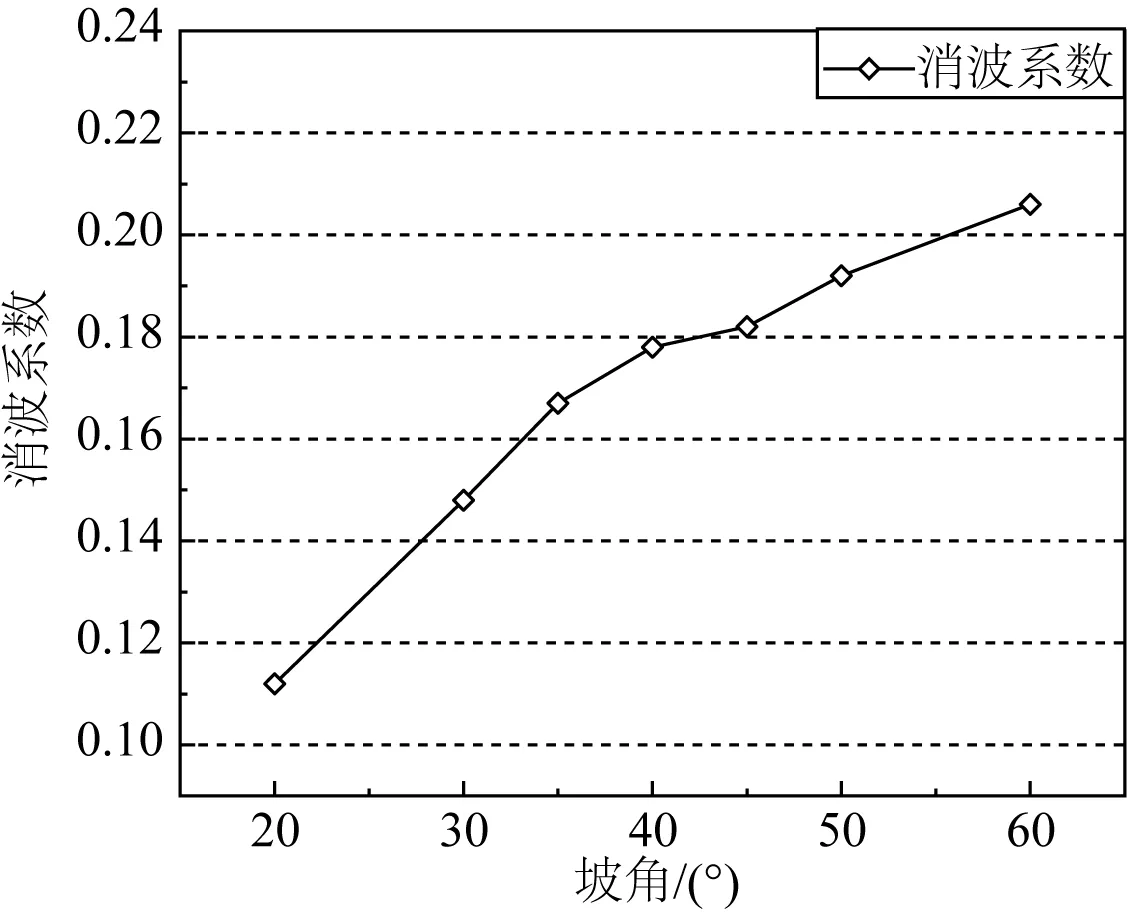
图7 不同坡角海堤的消波系数对比Fig. 7 Comparison of wave elimination coefficients at different angles

表2 不同坡角海堤的波浪峰值对比
Tab. 2 Comparison of wave-eliminating effects of seawalls with different slope angles

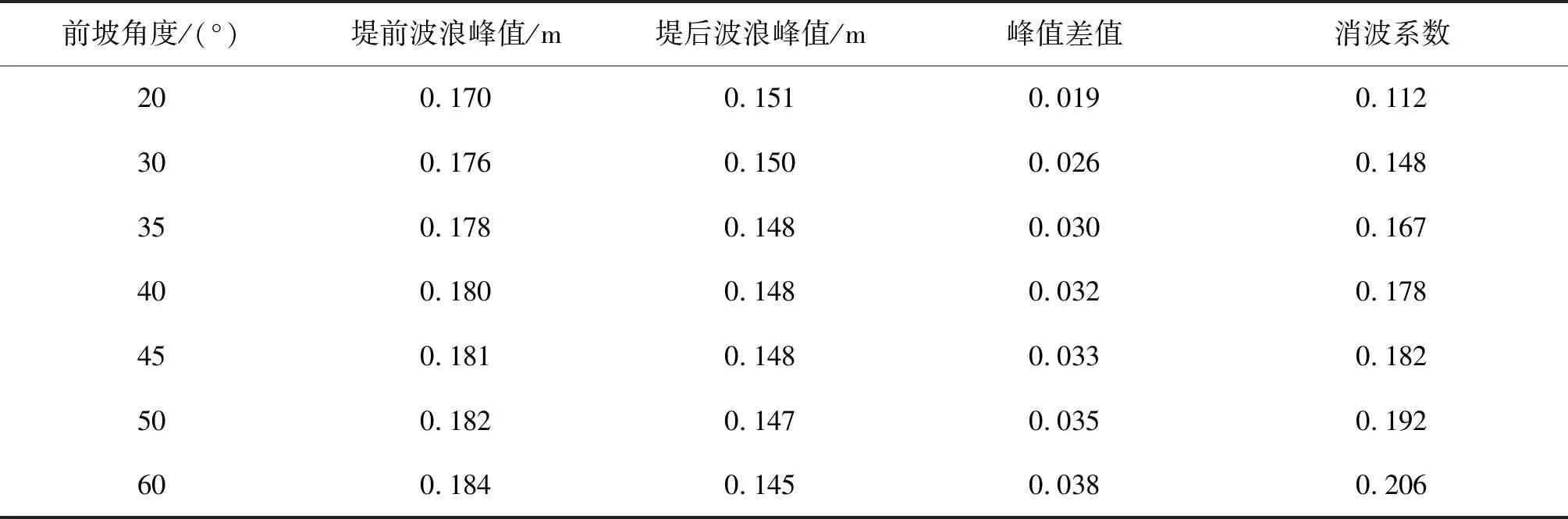
前坡角度/(°)堤前波浪峰值/m堤后波浪峰值/m峰值差值消波系数200.1700.1510.0190.112300.1760.1500.0260.148350.1780.1480.0300.167400.1800.1480.0320.178450.1810.1480.0330.182500.1820.1470.0350.192600.1840.1450.0380.206

如图8所示，进一步分析波浪衰减现象逐步加剧的原因。可以发现在波浪越堤传播到堤后浅水区时，其波峰变陡，波浪发生卷曲然后破碎，堤后波浪波陡较大且底坡平缓，此时出现了小范围内的崩破波流态。浅水冲刷最低位置上方出现波浪回流，回流水体落下后形成裹气波浪的冲击波形态[18]，此时能够清晰地捕捉到翻转水舌和裹气现象，崩破波流态下会产生剧烈能量耗散。随着波浪爬高的增加，堤前波浪的势能增大，堤后浅水冲刷最低位置继续降低，出现更为显著的崩破波形态，造成波浪更加急剧的能量耗散。这也解释了随着海堤坡角的递增，波浪爬升高度增大，消波系数呈现增大趋势，堤后波浪衰减现象更加明显的原因。

图8 不同时段崩破波演化数值模拟图Fig. 8 Numerical simulation of spilling breaker evolution from 1.76 s to 1.84 s

4 结 语

研究海啸波与海堤相互作用的水动力学问题，并将数值模拟结果与模型试验数据对比，得到结论如下：

1)根据数值模拟精度和计算总时长，粒子间距设置为0.002 m能够有效捕捉自由液面，同时引入固壁边界条件，减少坡角边界条件改变对计算域精度的影响；

2)准确地模拟了海堤对海啸波传播过程的影响，捕捉到射流、崩破波等一系列波浪强非线性现象，对比物理模型试验中的液位变化图，验证了数值模型的可靠性与准确性；

3)在波浪要素、堤顶水深等要素相同时，海堤坡角对海啸波的爬高与衰减影响显著，在20°～60°的海堤坡角范围内，随着坡度的增加，堤前波浪爬高增大，捕捉到剧烈的崩破波现象，波浪衰减进一步加剧。

4)当坡角较小时，随着坡角的增大，消波系数增长明显，防灾减灾效果提升；继续增大坡角时，消波系数增长缓慢，此时应考虑优化海堤结构，进一步提升消波效果。