不同雷诺数下倾斜圆柱绕流三维数值模拟研究
2020-04-10高洋洋张演明
高洋洋,张演明,刘 彩,王 滨
(1. 浙江大学 海洋学院,浙江 舟山 316021; 2. 中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122)
在海洋工程中,钢悬链线立管因其结构简单、经济可靠及对上部平台运动更好的适应性越来越多的被应用于深水油气资源开发中。钢悬链线立管近触底区由于倾斜角度变化大,在流体绕流倾斜立管的过程中,尾涡相互干扰机制更加复杂,更易导致立管发生疲劳破坏。然而目前基于竖直圆柱的尾涡特性研究因忽略轴向流影响,其尾流形态特征、受力特性及旋涡脱落频率与竖直圆柱相比存在明显差异。近年来,针对倾斜圆柱绕流的研究受到海洋工程界和学术界的广泛关注。
Shirakasi等[1]在倾斜圆柱绕流的风洞试验中发现了沿圆柱轴向的涡运动,且随倾角的增大旋涡脱落频率逐渐减小。李寿英和顾明[2]通过对升力系数进行功率谱密度分析发现竖直圆柱与倾斜圆柱绕流存在显著差异,在倾斜圆柱尾流中存在低频谐波。Hogan & Hall[3]研究表明随着倾斜角度的增大,倾斜圆柱绕流流场的三维效应愈发明显,不存在规则脱落的旋涡。Franzini等[4]通过物理模型试验进一步探讨了圆柱倾斜角度对尾流涡街的影响,研究发现当倾斜角度达到α=45°时,圆柱后方的轴向流会对圆柱表面自由剪切层之间的相互作用造成一定影响,使得尾流的旋涡脱落变得不规则。Mstsumoto等[5-6]指出,圆柱后方轴向流的作用类似于分流板,即轴向流会影响自由剪切层的相互作用,降低旋涡脱落的强度。为了简化计算,通常采用独立性原则(independence principle,简称IP)进行倾斜圆柱绕流特性研究,该原则认为,在不同倾斜角度下,通过垂直于圆柱轴线的速度分量计算得到的升阻力系数及旋涡脱落频率趋于一致[7]。Vakil & Green[8]开展了低雷诺数下不同长细比及倾斜角度条件下圆柱绕流的数值模拟研究,研究发现当倾斜角度大于45°时,独立性原则不再适用。Zhao等[9]研究发现当雷诺数达到Re=1 000时,在小倾角情况下,阻力系数均值与无量纲涡脱频率St数适用于独立性原则,相反,升力系数均方根值不符合独立性原则。Thapa等[10]开展了近壁面倾斜圆柱绕流的数值模拟研究,研究结果表明由于边界效应的影响,随着倾斜角度的不断增大,流场的三维特性逐渐减弱。梁辉等[11]研究了倾斜圆柱绕流的展向特性,归纳了不同展向截面处的不同涡脱形态。Hu等[12]采用高速粒子测速技术(PIV)开展了方柱绕流的试验研究,发现方柱后侧的轴向流会对尾流流场特征产生显著的影响,随着倾斜角度的增大,顺流向方柱出现自底端流向顶端的轴向流动,而逆流向方柱出现自顶端流向底端的轴向流动。
综上所述,当前针对圆柱绕流的研究主要集中于竖直圆柱绕流及单一雷诺数条件下同一倾斜方向圆柱绕流特性研究,不同倾斜方向及雷诺数对倾斜圆柱绕流的流场形态及受力特性的影响规律尚未阐明。因此,采用计算流体力学开源代码OpenFOAM开展了不同雷诺数、倾斜方向及倾斜角度条件下倾斜圆柱绕流的三维数值模拟研究,主要分析了瞬时及时均三维流场形态、流线拓扑及轴向流分布特征,揭示了倾斜圆柱尾流特征、受力特性及旋涡脱落频率随倾斜角度、雷诺数及倾斜方向变化的影响规律,阐明了不同雷诺数条件下独立性原则(IP)的适用范围。
1 数学模型
1.1 控制方程
在直角坐标系中,不可压缩黏性流体在层流状态下的连续方程和动量守恒方程Navier-Stokes(N-S)方程为:
·U=0
(1)
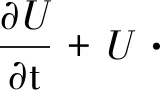
(2)
其中,U,p,ρ和υ分别表示速度矢量、压力、流体密度和流体动力黏度。
大涡模拟控制方程可由湍流状态下将N-S方程进行滤波处理得到[13-17],如式(3)-(4)所示:
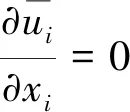
(3)
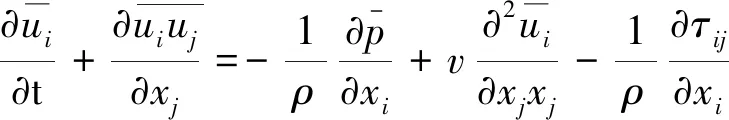
(4)
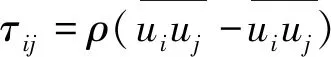
利用有限体积法进行离散。在层流工况下采用icoFoam算法进行速度与压力耦合,压力与拉普拉斯项采用二阶高斯线性正交格式进行离散,时间项采用一阶隐式进行离散,梯度与散度项采用高斯线性进行离散。在湍流工况下采用pisoFoam算法进行速度与压力耦合,压力项和拉普拉斯项采用二阶高斯线性正交格式进行离散,时间项采用二阶隐式进行离散,梯度与散度项采用高斯线性进行离散。
1.2 计算域及边界条件设置
倾斜圆柱绕流流场计算域如图1所示,计算域长度和宽度分别取L=30D和W=20D,其中D表示圆柱直径,取D=0.01 m。圆柱底部横截面的中心与计算域入口的距离为10D,同时根据Behr等[18]的研究结果,圆柱距离两侧壁的距离设置为10D。计算域展向高度设为Z=πD,与文献[19-20]保持一致,从而保证流场在展向得到充分发展,准确捕捉倾斜圆柱的三维涡脱。圆柱倾角α表示来流速度与圆柱法线的夹角,如图1(b)所示。整个计算域的初始速度与压力均设置为0,入口设置为自由来流边界,入口速度设置分别为u=u0=0.01 m/s、0.15 m/s和0.39 m/s,对应不同的雷诺数Re=100、1 500和3 900,而横流向与展向速度设置为v=w=0;出口设置为自由出流边界条件;两侧壁面设置为对称边界,即法向速度与压力的梯度为0;上下两壁面设置为零梯度边界,即所有变量沿法向梯度为0;圆柱表面设置为无滑移壁面,即u=v=w=0。具体边界条件设置详见表1。在层流工况下,基于前人关于圆柱绕流研究[21-23],雷诺数采用Re=100,在该雷诺数下圆柱绕流流场呈现明显的二维特性。在湍流工况下,前人关于圆柱绕流流场的实验及数值模拟研究大多采用雷诺数Re=1 500[24-26]和3 900[4,13-14],当Re=1 500和3 900时,湍流流场均得到充分发展。因此,在本研究中采用直接模拟方法和Smargorinsky-Lilly亚格子模式的大涡模拟(LES)湍流模型开展Re=100、1 500和3 900下倾斜圆柱绕流研究,分析不同雷诺数对倾斜圆柱绕流流场的影响。倾斜角度范围为-60° ≤α≤ 60°,每间隔15°设为一组,共9组工况,其中正值和负值分别表示圆柱沿顺流向倾斜和逆流向倾斜。

图1 计算域和倾斜角度αFig. 1 Computational domain and definition of the inclined angle α
表1 边界条件设置
Tab. 1 Boundary conditions

边界条件设定入口自由来流u=u0=0.01 m/s、0.15 m/s和0.39 m/s,v=w=0出口自由出流u/x=0, P=0两侧边界对称边界∂u/∂y=0,∂w/∂y=0,v=0;∂P/∂y=0上下边界零梯度边界u/z=0,P/z=0圆柱表面无滑移边界u=v=w=0
1.3 网格及时间步验证
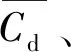
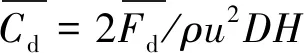
(5)
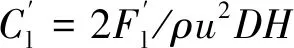
(6)
St=fsD/u
(7)
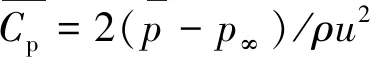
(8)
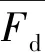

图2 倾斜圆柱绕流流场计算网格(α=30°)Fig. 2 Schematic view of the computational mesh(α=30°)
表2 竖直圆柱绕流模型网格信息
Tab. 2 The details of three different meshes for flow past a single vertical cylinder

网格密度粗网格中网格细网格网格总单元数666 7541 174 0081 259 218圆柱节点数100100120展向结点数255050
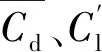
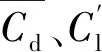
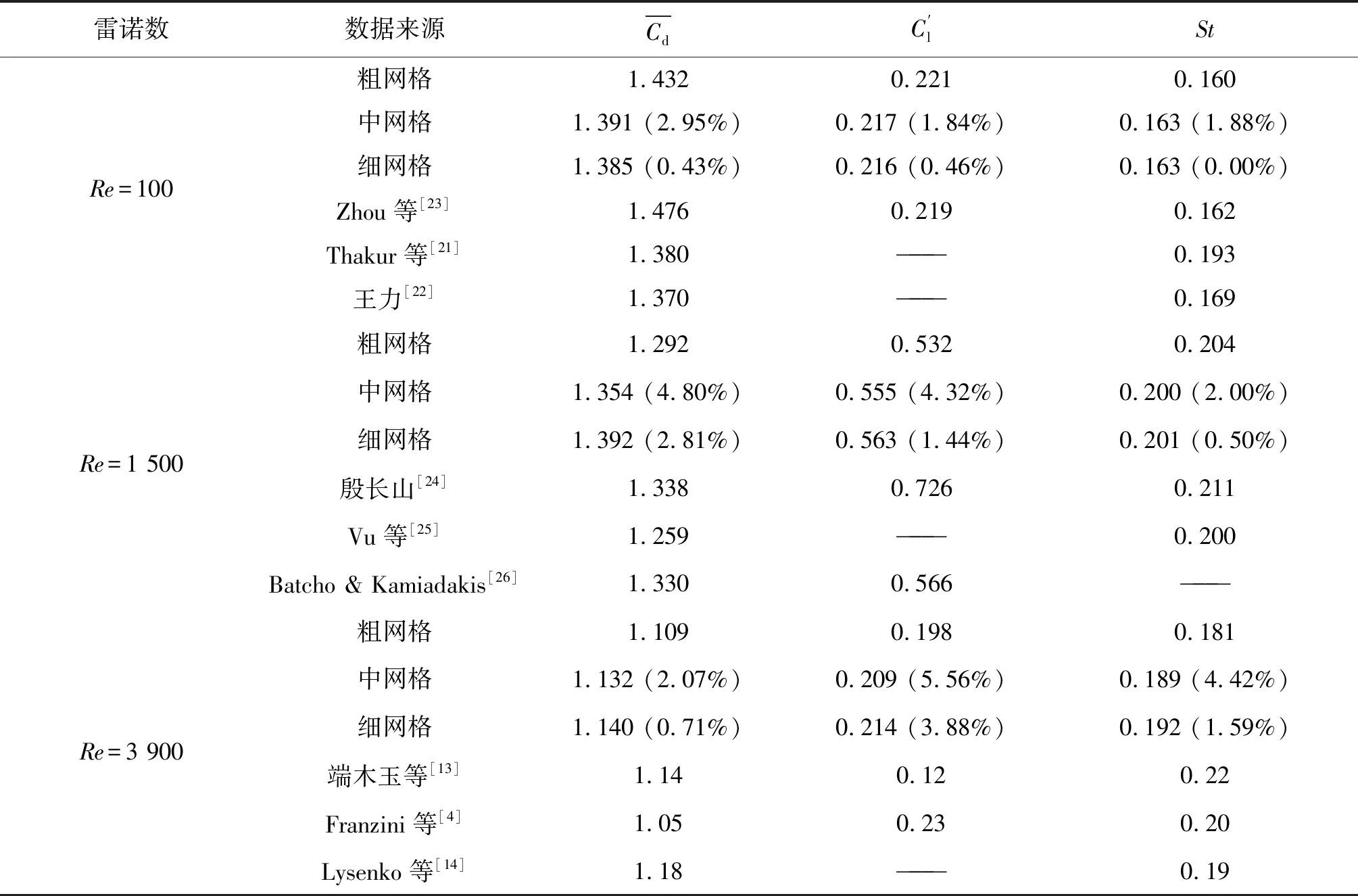
表3 不同网格结果对比(α=0°, Re=100、1 500和3 900)Tab. 3 Comparisons between the present results and previous literature (α=0°, Re=100, 1 500 and 3 900)
表4 不同时间步长结果对比(α=0°,Re=100、1 500和3 900)
Tab. 4Comparison of the results for a single vertical circular cylinder with different time steps (α=0°,Re=100, 1 500 and 3 900)
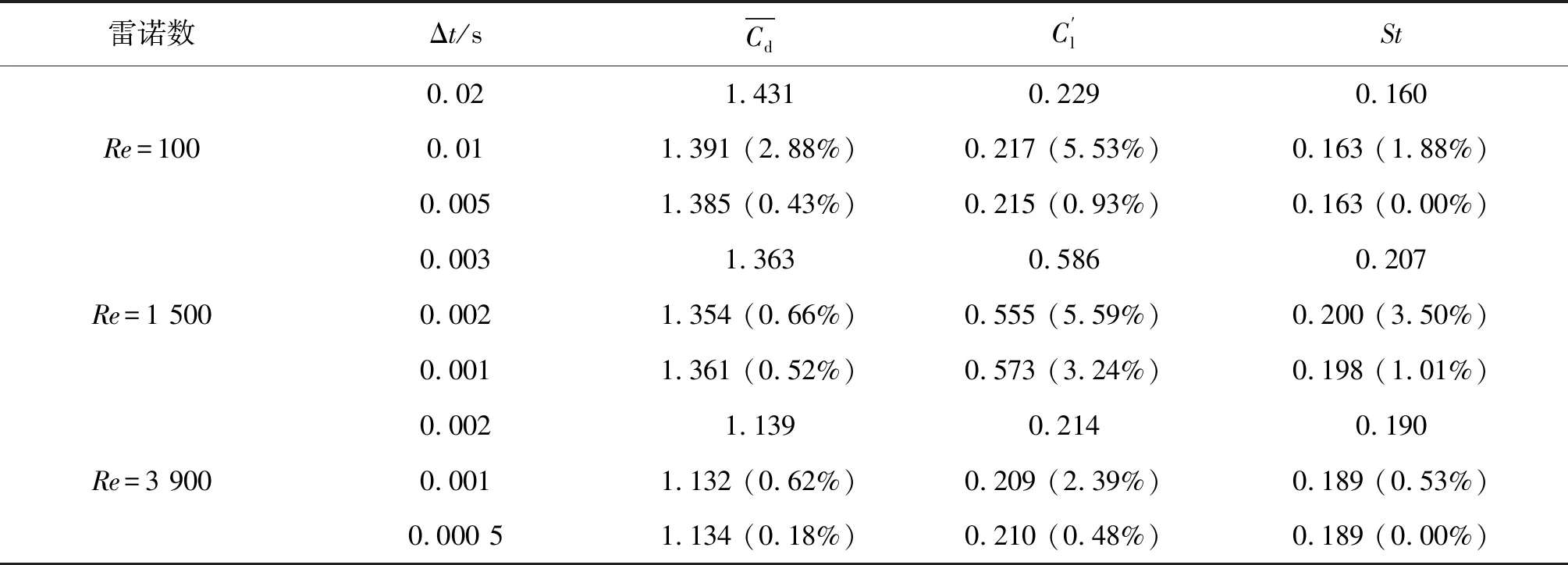
雷诺数Δt/sCdC′lStRe=1000.021.4310.2290.1600.011.391 (2.88%)0.217 (5.53%)0.163 (1.88%)0.0051.385 (0.43%)0.215 (0.93%)0.163 (0.00%)Re=1 5000.0031.3630.5860.2070.0021.354 (0.66%)0.555 (5.59%)0.200 (3.50%)0.0011.361 (0.52%)0.573 (3.24%)0.198 (1.01%)Re=3 9000.0021.1390.2140.1900.0011.132 (0.62%)0.209 (2.39%)0.189 (0.53%)0.000 51.134 (0.18%)0.210 (0.48%)0.189 (0.00%)
2 结果与讨论
2.1 瞬时流场
采用Hunt等[27]推荐的Q准则绘制了不同雷诺数及不同倾角情况下圆柱绕流的三维无量纲瞬时涡量等势面图,如图3~图5所示。在低雷诺数Re=100和高雷诺数Re=1 500和3 900时Q取值分别为0.1和100。在低雷诺数Re=100情况下,在-45° ≤α≤ 45°范围内,倾斜圆柱三维尾涡结构均较为规则,尾流涡管与圆柱近乎平行,随着圆柱倾角的变化而变化,几乎无展向变形,表现出极强的二维特性。然而,在大倾角α=± 60°条件下,旋涡脱落完全被抑制,圆柱后方已不存在涡管,无旋涡脱落发生。当雷诺数Re增大至1 500和3 900时,对于竖直圆柱(α=0°)而言,圆柱尾流并未出现明显的展向掺混,但尾涡结构在展向上存在一定的相位差异,圆柱尾流涡街较为规则;当倾角增大至|α|=15°时,流场的展向掺混现象明显,尾流涡街仍较为规则;而当倾角继续增大至|α| ≥ 30°时,圆柱尾流涡街的形态会发生明显变化,沿圆柱轴向方向会产生较强的轴向流。在大倾角 |α|=45°和60°条件下,圆柱尾流涡脱会受到较大程度的抑制,从瞬时涡量图中可以看出,圆柱后方尾流仅存在沿展向分布的涡管。在雷诺数Re=3 900情况下,流场的展向掺混更为强烈,三维特性更加明显。
综上所述,随着圆柱倾角的增大,尾流旋涡的脱落与涡街的形成会逐渐受到抑制,细碎旋涡逐渐消失,尾流宽度也随之减小。随着雷诺数的增加,圆柱尾流涡管会发生明显的变形,展向掺混随着雷诺数的增大而愈发明显,导致出现大量细碎旋涡,呈现出明显的三维特性。在相同倾斜角度下,顺流向倾斜圆柱与逆流向倾斜圆柱后方的尾涡结构之间的差异非常小,不存在明显的区别,说明沿顺流向倾斜圆柱自底端流向顶端的轴向流动与沿逆流向倾斜圆柱自顶端流向底端的轴向流动对流场的影响较为一致。

图3 Re=100时不同倾角瞬时无量纲涡量Q =0.1等势面图Fig. 3 Instantaneous iso-surface of vorticity contours at different inclined angles for Re=100 (Q =0.1)
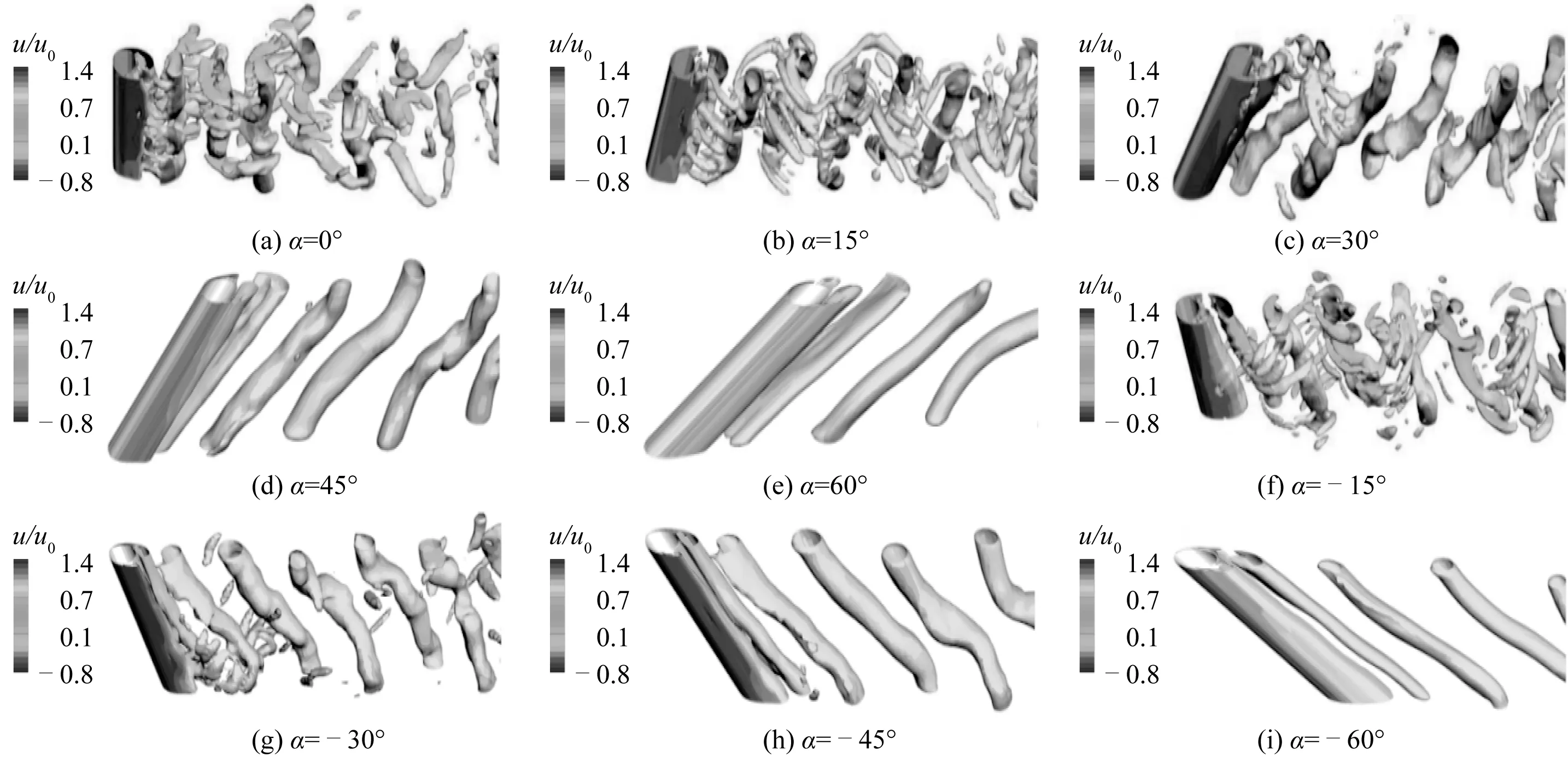
图4 Re=1 500时不同倾角瞬时无量纲涡量Q =100等势面图Fig. 4 Instantaneous iso-surface of vorticity contours at different inclined angles for Re=1 500 (Q =100)
图5 Re=3 900时不同倾角瞬时无量纲涡量Q =100等势面Fig. 5 Instantaneous iso-surface of vorticity contours at different inclined angles for Re=3 900 (Q =100)
图6~图8分别表示雷诺数Re=100、1 500和3 900情况下不同倾角条件下瞬时三维流线图。当雷诺数Re=100时,除|α|=60°外,圆柱尾流流场几乎不存在展向掺混,流线十分规则且近乎平行,而当倾角|α|=15°时,在圆柱后方的轴向流动呈现较为明显的螺旋形态。当雷诺数增大至Re=1 500和3 900时,圆柱后方的三维流线形态较为近似且三维特性明显:对于竖直圆柱(α=0°)而言,在圆柱后方存在回流区,随着流动逐渐往下游发展,旋涡消失,流线变得较为规则;当倾角增大至|α|=15°,在圆柱后方存在回流区,此外,在圆柱后方观测到较为明显的呈螺旋运动形态的轴向流动;当倾角进一步增大至 |α| ≥ 30°时,圆柱后方的旋涡逐渐消散,轴向流更加明显,轴向流到达圆柱下端后继续向下游发展。在相同倾斜角度下,沿顺流向倾斜圆柱与逆流向倾斜圆柱的轴向流强度几乎相同,沿顺流向倾斜圆柱出现自底端流向顶端的轴向流动,而沿逆流向倾斜圆柱出现自顶端流向底端的轴向流动。
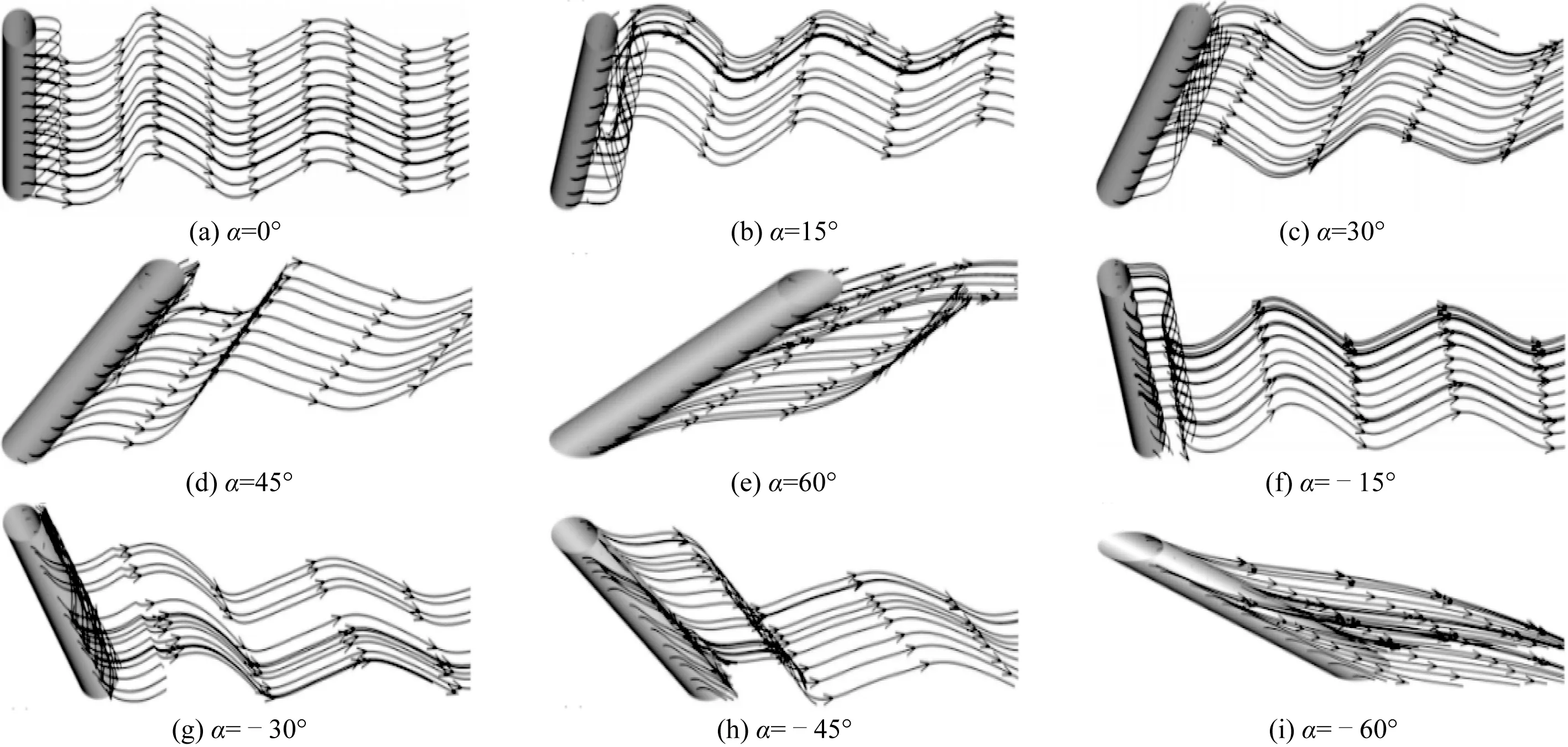
图6 Re=100时不同倾角瞬时三维流线Fig. 6 Instantaneous three-dimensional streamline at different inclined angles for Re=100

图7 Re=1 500时不同倾角瞬时三维流线Fig. 7 Instantaneous three-dimensional streamline at different inclined angles for Re=1 500
图8 Re=3 900时不同倾角瞬时三维流线Fig. 8 Instantaneous three-dimensional streamline at different inclined angles for Re=3 900
2.2 时均流场
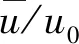
综上所述,随着雷诺数的增大,倾斜圆柱绕流的尾流流线愈加混乱,流场的三维特性愈加明显。随着倾角的变化,尾流回流区的存在范围也会发生改变,当雷诺数Re=100和1 500时,在小倾角|α| ≤ 15°条件下,倾斜圆柱尾流中存在一定范围的回流区,在大倾角 |α| ≥ 30°条件下,回流区完全消失;而当雷诺数Re=3 900时,在|α| ≤ 30°条件下存在回流区。在相同倾斜角度下,顺流向倾斜圆柱与逆流向倾斜圆柱后方的回流区宽度一致,时均流线形态几乎对称,沿顺流向倾斜圆柱出现自底端流向顶端的轴向流,而沿逆流向圆柱出现自顶端流向底端的轴向流。
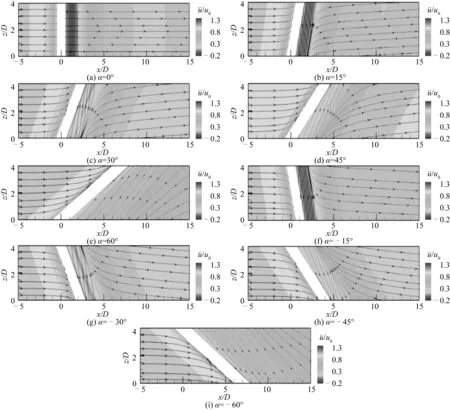
图9 Re=100时在y/D=0断面处不同倾角的时均流线图Fig. 9 Time-averaged streamline topologies at different inclined angles for Re=100

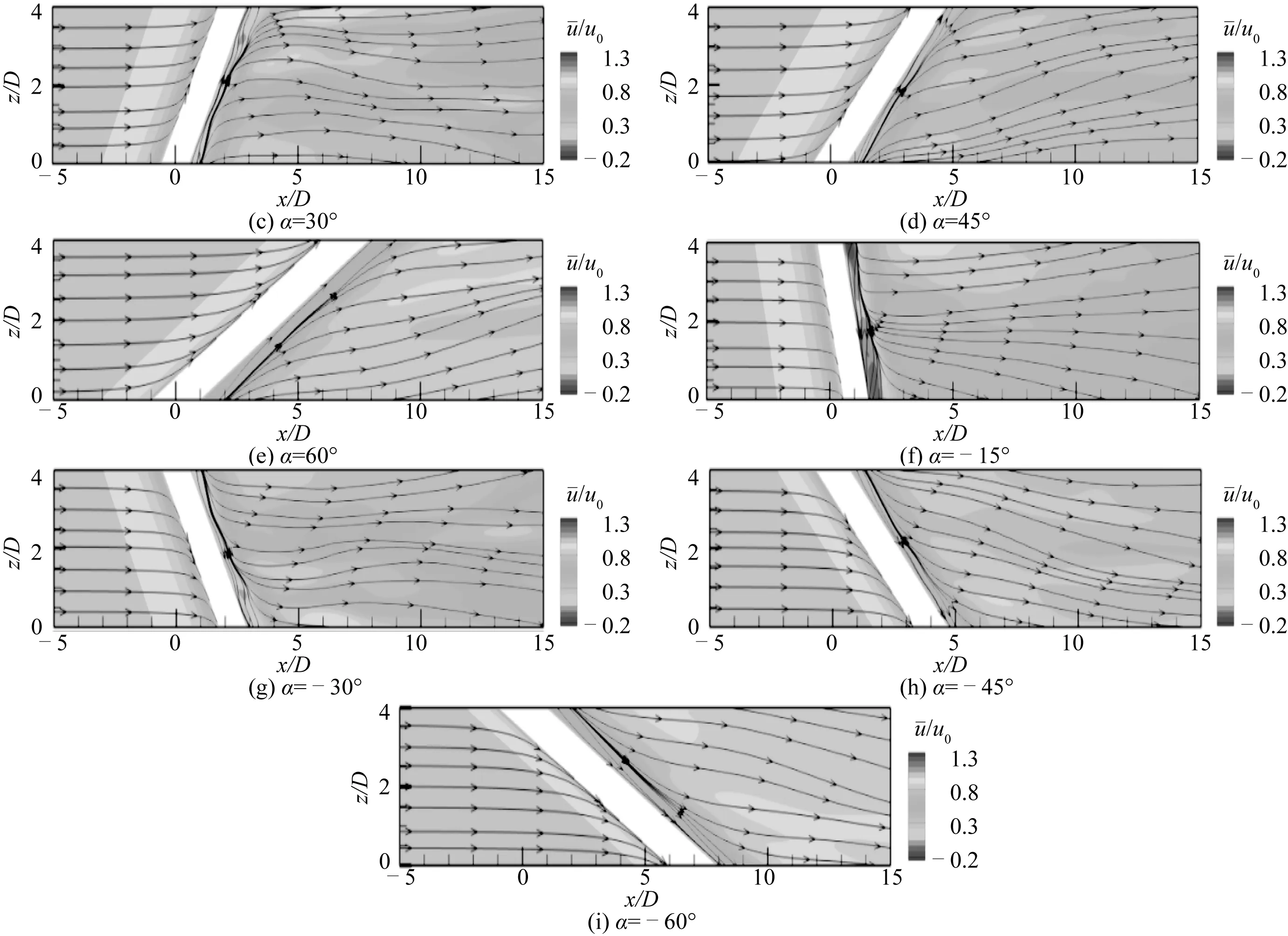
图10 Re=1 500时在y/D=0断面处不同倾角的时均流线图Fig. 10 Time-averaged streamline topologies at different inclined angles for Re=1 500

图11 Re=3 900时在y/D=0断面处不同倾角的时均流线图Fig. 11 Time-averaged streamline topologies at different inclined angles for Re=3 900
2.3 倾斜圆柱受力特性及旋涡脱落频率

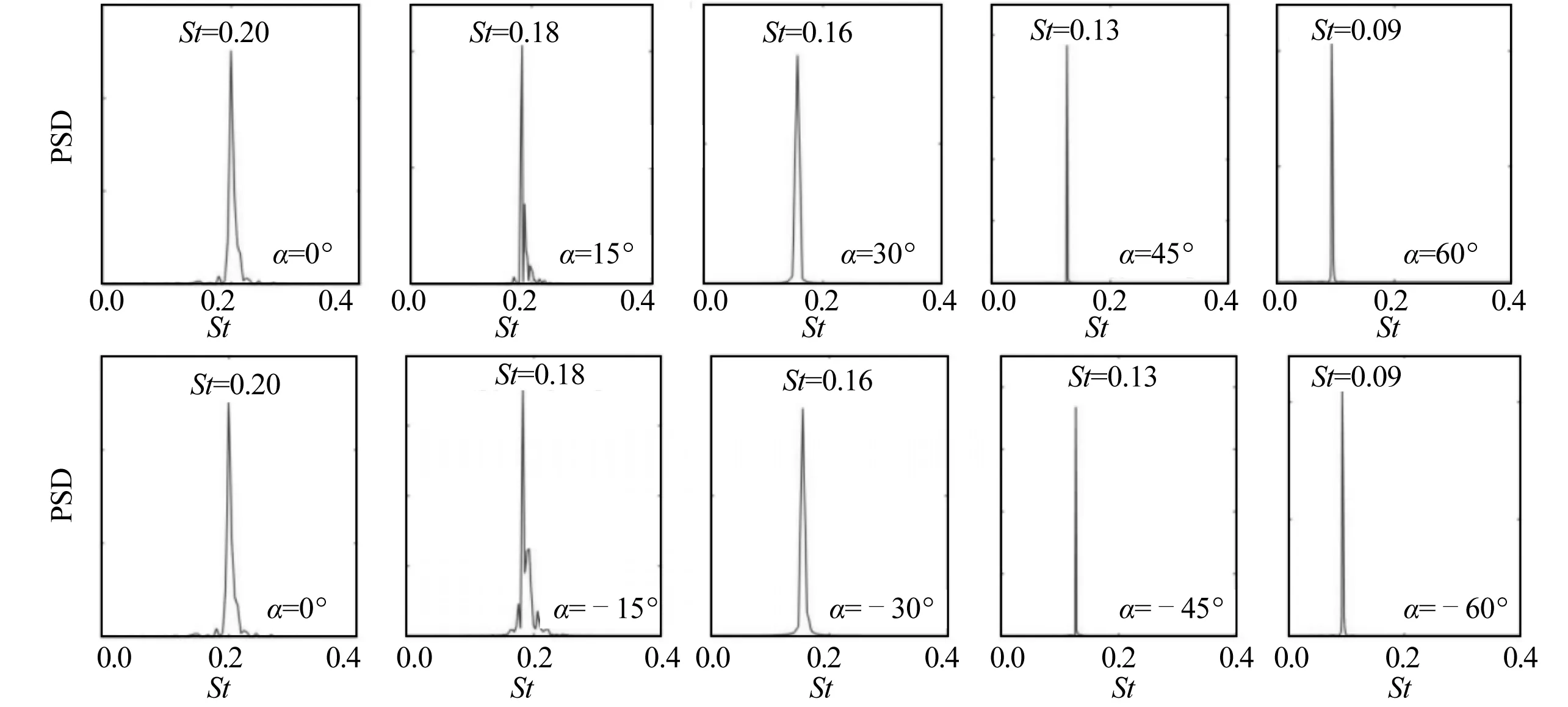
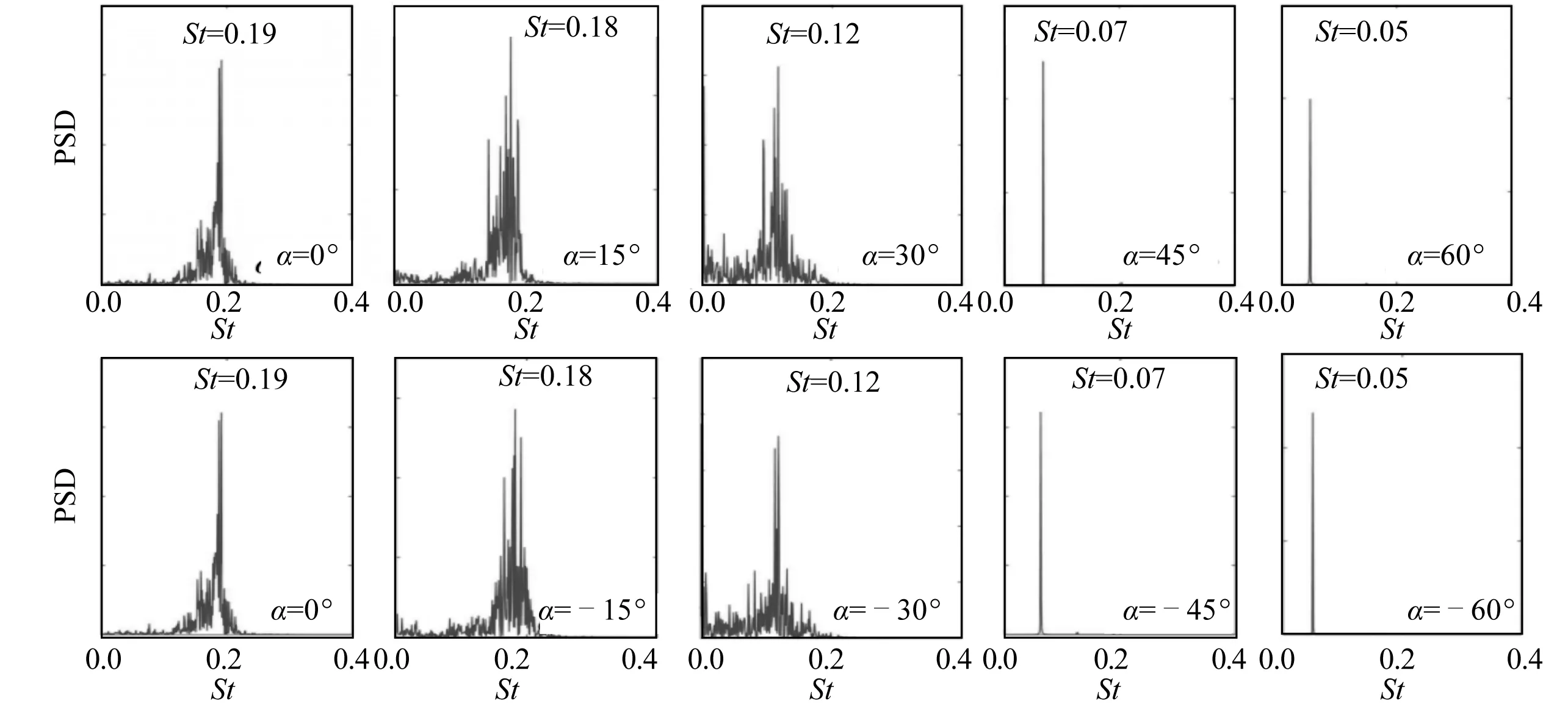
通过对不同雷诺数及倾斜角度下圆柱所受升力系数进行快速傅里叶变换(FFT),开展频谱分析得到无量纲旋涡脱落频率Strouhal数,如图13~图15所示。在雷诺数Re=100、1 500和3 900情况下,竖直圆柱对应的St数分别为0.16、0.20和0.19,与Zhou等[23]和Vu等[25]所得结果较为接近,对应的频谱峰值均单一且明显。当雷诺数Re=100时,随着圆柱倾角的不断增大,St数呈单调递减的趋势,当|α|=60°时旋涡脱落已被完全抑制,因此不存在St数。当雷诺数Re=1 500时,倾角|α| ≥ 15°情况下,虽然圆柱尾涡结构会受到轴向流的影响,但对应的频谱峰值仍比较单一,倾角|α|=45°和60°时对应的St数分别为0.13与0.09。当雷诺数Re=3 900时,倾角|α|=15°情况下,由于轴向流的存在导致轴向涡脱和尾流不规则涡脱,在频谱主峰值的附近存在幅值较低的谐波。当倾角进一步增大到|α|=30°时,St数在0 图13 Re=100时不同倾角的St数Fig. 13 Strouhal number at different inclined angles for Re=100 图14 Re=1 500时不同倾角的St数Fig. 14 Strouhal number at different inclined angles for Re=1 500 图15 Re=3 900时不同倾角的St数Fig. 15 Strouhal number at different inclined angles for Re=3 900 图16 无量纲涡脱频率St数随倾角的变化曲线Fig. 16 Strouhal number as a function of the inclined angle 图17 独立性原则验证Fig. 17 Validation of IP 对不同雷诺数(Re=100、1 500和3 900)和不同倾斜角度(-60°≤α≤ 60°)工况下沿顺流向与逆流向倾斜的圆柱绕流流场开展了三维数值模拟研究,主要揭示了三维瞬时及时均尾流流场、流线拓扑、升阻力系数及旋涡脱落频率随雷诺数及倾斜角度变化的规律,验证了独立性原则(IP)的适用性,得到的主要结论如下: 1) 随着圆柱倾斜角度的增大,倾斜圆柱尾流产生较为明显的轴向流,尾流旋涡脱落受到明显抑制,细碎旋涡逐渐消失,尾流宽度也随之减小;随着雷诺数的增大,圆柱尾流涡管发生明显的变形,展向掺混使得大量细碎旋涡产生,呈现出明显的三维特性。 2) 随着倾斜角度的增大,倾斜圆柱尾流回流区逐渐消失,当雷诺数Re=100和1 500时,在倾角 |α| ≥ 30°条件下,回流区完全消失;当雷诺数Re=3 900时,在|α| ≥ 45°条件下,回流区消失。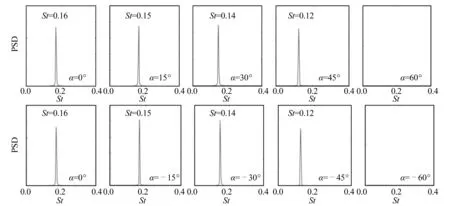
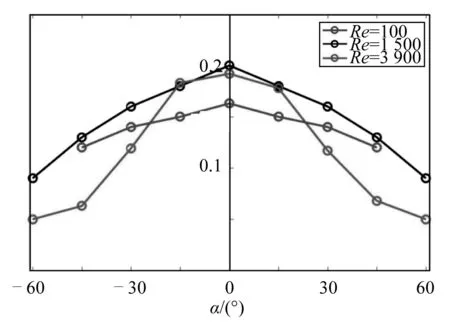

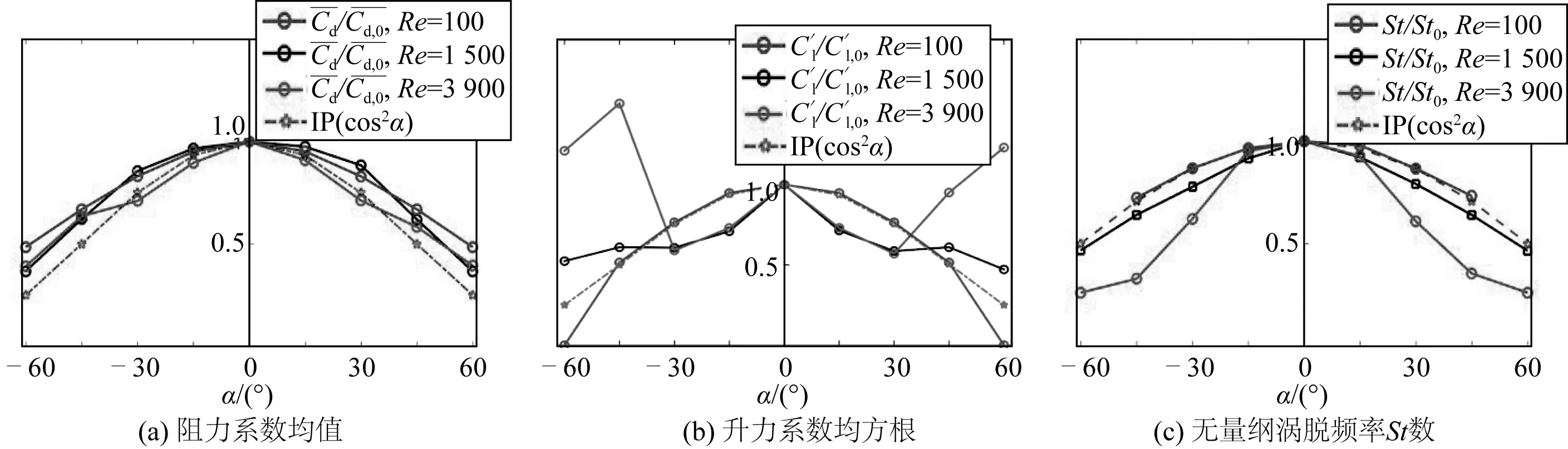
2.4 独立性原则验证
3 结 语