格构式钢柱在冲击作用下动态响应的有限元分析

2020-04-10张永胜郭昭胜

科学技术与工程 2020年4期

崔凯，张永胜，郭昭胜

(太原理工大学土木工程学院，太原 030024)

格构式钢柱多由型钢或钢板设计成的双轴或单轴对称截面，具有环保、高效的特点，拥有较好的承载力和抗扭性能，是常见的钢结构类型，在工民建领域具有重要的地位。然而建筑结构在服役期间，各种类型的结构及其部件会不可避免地受到不同程度的冲击，譬如以热力管道活动支架为例的悬臂钢柱在使用过程中遭到行驶车辆的意外冲击，或者厂房中由于屋架作用而视为固简约束的排架柱因吊车吊起重物时的操作不慎而受到侧向冲击碰撞等，会对人类造成财产损失甚至对人身安全造成威胁。随着格构式构件在钢结构领域的广泛应用，对其冲击荷载下的动态响应和力学性能的研究变得尤为重要。

中外学者对钢管及钢管组合结构、实腹式型钢结构、钢筋混凝土等结构的冲击受损做了大量研究，蔡健等[1]、王潇宇等[2]、Huang等[3]对不同形式和约束情况的钢管组合结构进行落锤冲击试验，得出壁厚、尺寸、形式、重量等因素是影响钢管组合结构侧向冲击性能的重要因素，并简化计算方法；王蕊等[4]、崔娟玲等[5]、弓磊等[6]对研究受冲击后H型钢柱的力学性能进行研究，计算其剩余承载力系数，得出冲击能量与局部损伤变量之间的线性的函数关系；Demartino等[7]、Cai等[8]、Pham等[9]对钢筋混凝土构件进行了一系列冲击试验，并与经验公式进行对照,研究其冲击作用下的力学性能。

目前，中国有关格构式构件在冲击荷载下的动态响应和力学性能文献较少[10-11]，对格构式构件的研究可以进一步挖掘开发，因此，基于Abaqus/Explicit的显示中心插值算法，探索在不同冲击作用下，悬臂式钢柱在侧向冲击作用下的动态响应，并对其抗冲击性能进行研究。

1 试验简介以及模型验证

1.1 试验概述

文献[11]通过控制落锤下落高度对6个规格相同的格构式钢柱进行侧向冲击试验，试件为两端铰支约束，材料为Q235低碳素钢，柱肢规格为L50 mm×5 mm，两端缀板采用-5 mm×80 mm×150 mm长缀板，中间缀板采用-5 mm×80 mm×100 mm钢板，各缀板间距100 mm，试件两端焊接-20 mm×220 mm×220 mm的端板，试件总长度为1.44 m。落锤总重203.9 kg，底面尺寸为80 mm×30 mm，下落高度分别为0.5、0.7、1.1 m。试验采用动态应变仪记录试件在冲击力作用下冲击力时程曲线，并记录肢件测点相对变形量。

1.2 模型的建立

采用Abaqus/Explicit有限元程序对文献[11]中格构式钢柱落锤冲击试验进行模拟和分析。钢柱和落锤采用Solid实体单元组合而成，其中落锤通过的*Rigid Body约束为刚体，质量由密度控制。钢材采用文献[12]提供的应力-应变关系模型，关系曲线分为：弹性、弹塑性段、塑性、二次流塑四个阶段。由于在冲击荷载下应变率强化作用，为达到预期的模拟目标，采用Cowper-Symend模型描述材料应变率，模型中参数由文献[6]统一取D=6 844 s-1、p=3.91。材料参数采用文献[11]实测数据如表1所示。

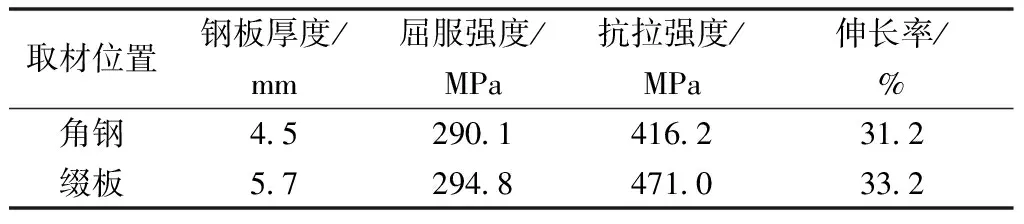
表1 钢材的材料性能参数Table 1 Material properties of steel

模型分析时给落锤施加不同冲击速度反映高度，落锤和钢柱表面之间接触定义为通用接触，其中法线方向定义为“hard”接触，切向方向按照“penalty”接触，摩擦系数设为0.4。另外缀板、角钢、端板之间焊接连接，采用*tie约束，即视为各个焊缝在冲击过程中不发生相对位移。模型中通过*coupling约束将构件端板节点耦合，设置参考点转角与位移使得试件为两端简支约束。网格划分过程中，模型全部采用C3D8R单元划分，网格最大不超过10 mm，冲击试验模型网格划分图如图1所示。

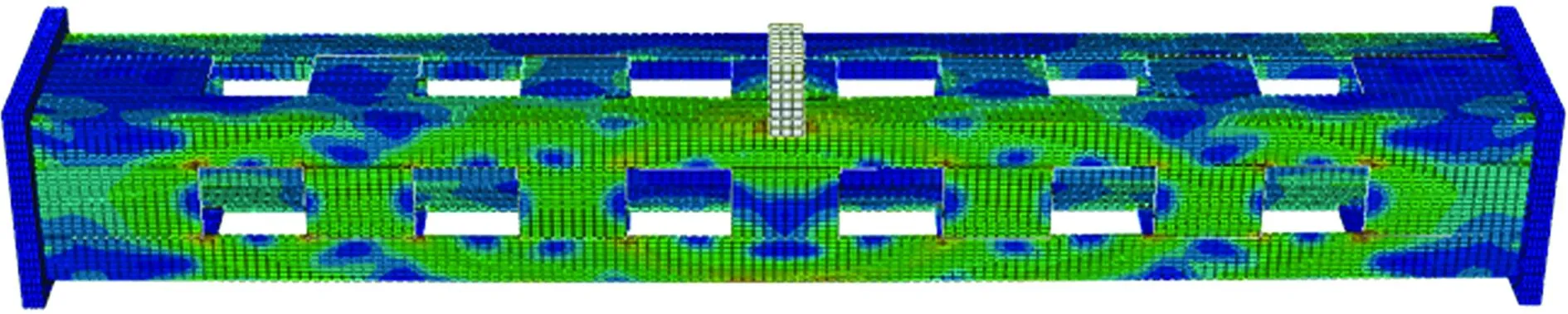
图1 钢柱受冲击有限元模型Fig.1 Finite element model of steel columnsubjected impact load

1.3 模型的验证

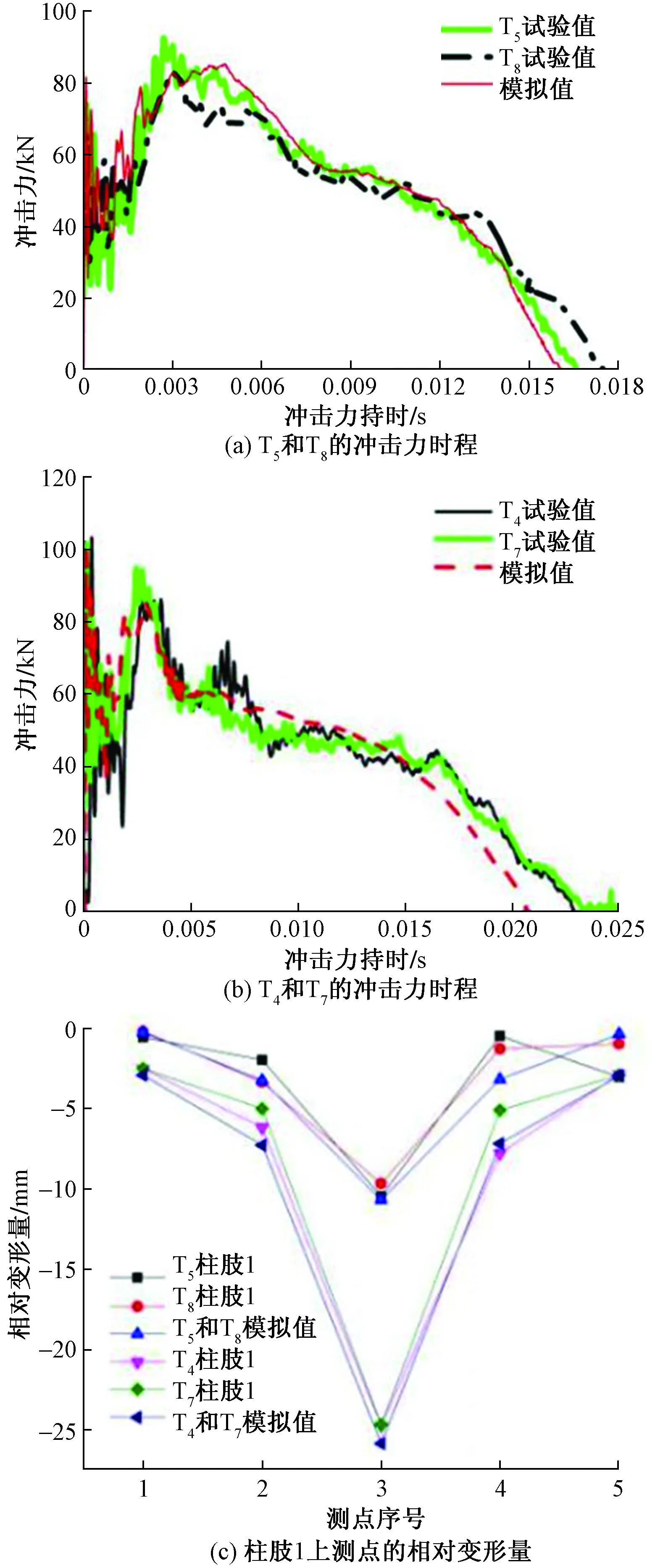
图2 数值模拟与试验对比Fig.2 Comparison between numerical and experimental

试验中每两个试件为同一工况，图2给出工况1(试件T5、T8)与工况2(试件T4、T7)下冲击力时程曲线与柱肢1相对变形量的数值模拟与试验结果对比图。由图2可知，两者冲击力时程曲线吻合良好，冲击力峰值与冲击力平台值非常接近，冲击力持时比试验稍短。试验与模拟柱肢1测点相对变形量的偏差较小，模拟值略大于试验值,表2给出了柱肢中间测点的相对变形量，柱肢跨中相对变形量最大差值在2.32 mm以内，证明模型的有效性。

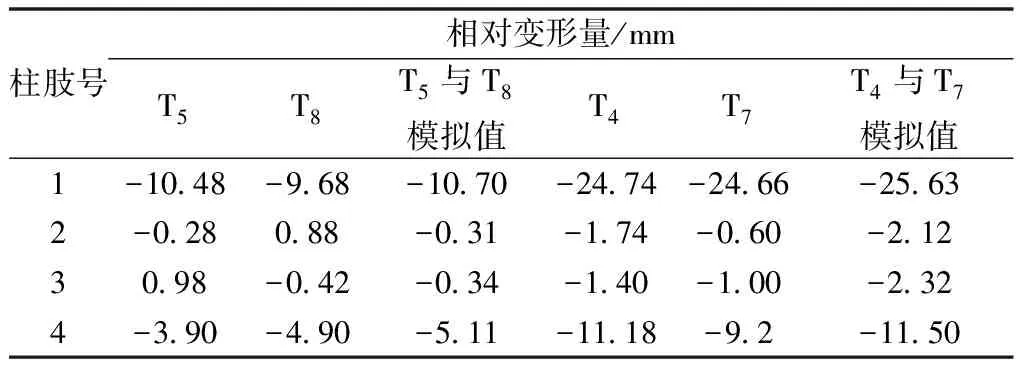
表2 柱肢中间测点的相对变形量Table 2 Relative deformation of measuringpoints on limb middle

注：柱肢挠度值为正值时，挠度向上；柱肢挠度值为负值时，挠度向下。

2 格构式钢柱的有限元分析

2.1 模型的建立

基于上述结果比较，证明该数值方法具有一定的可靠性。现以某厂房热力管道活动支架的悬臂格构式钢柱为例，研究其在侧向冲击下的力学性能，研究不同冲击位置与冲击能量下悬臂式格构柱的抗冲击性能。

在上述试验的模型的基础上，约束条件改为一端固定，一端自由。落锤底面尺寸为30 mm×180 mm，质量保持不变。冲击速度控制根据规范GB 4387—2008[13]有关限速要求选用冲击速度依次为4.75、5.42、6.34 m/s，冲击位置为缀板中心处，具体冲击位置如图3所示，试件基本参数如表3所示。

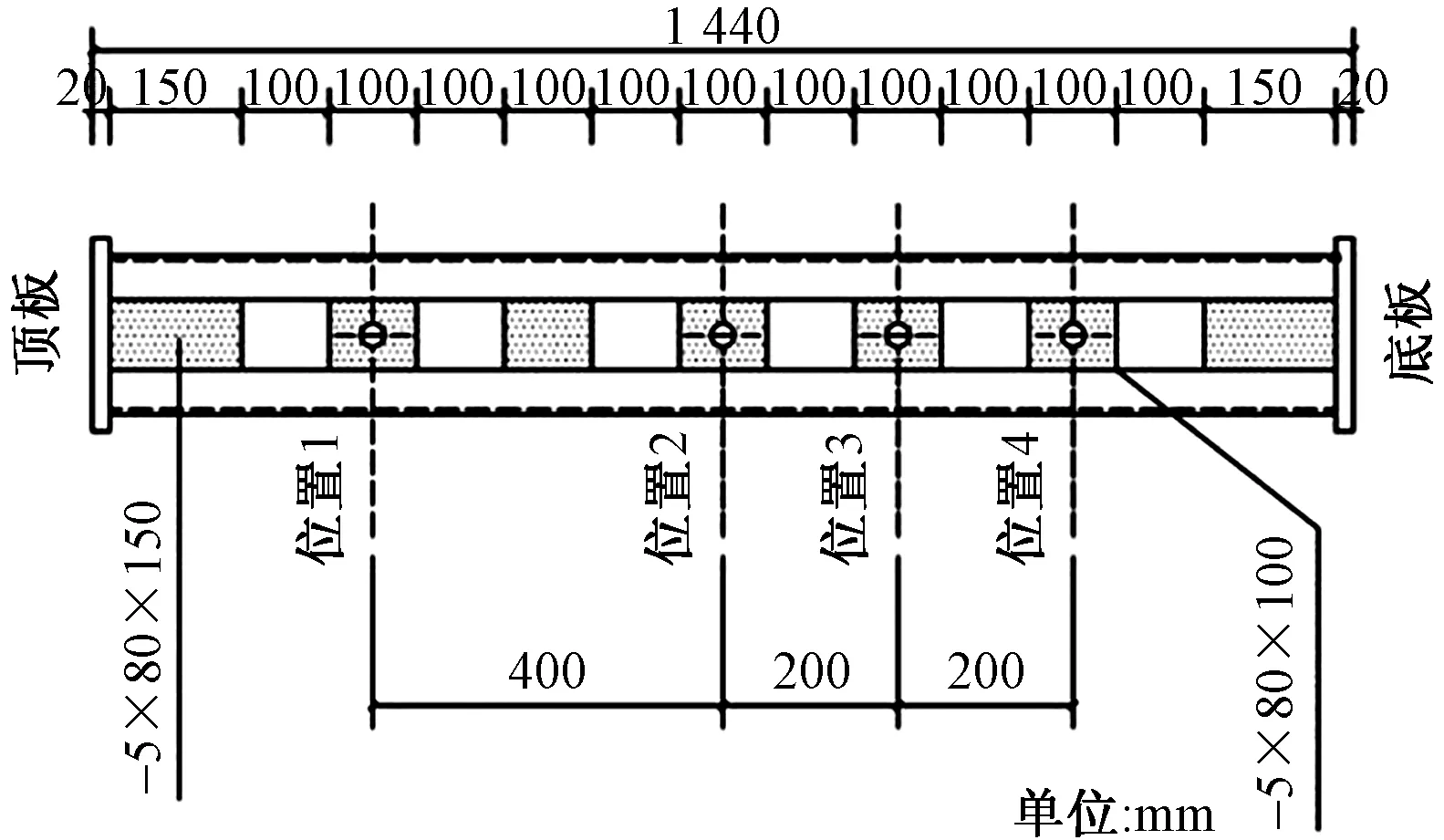
图3 冲击位置图Fig.3 Positions drawing of impact

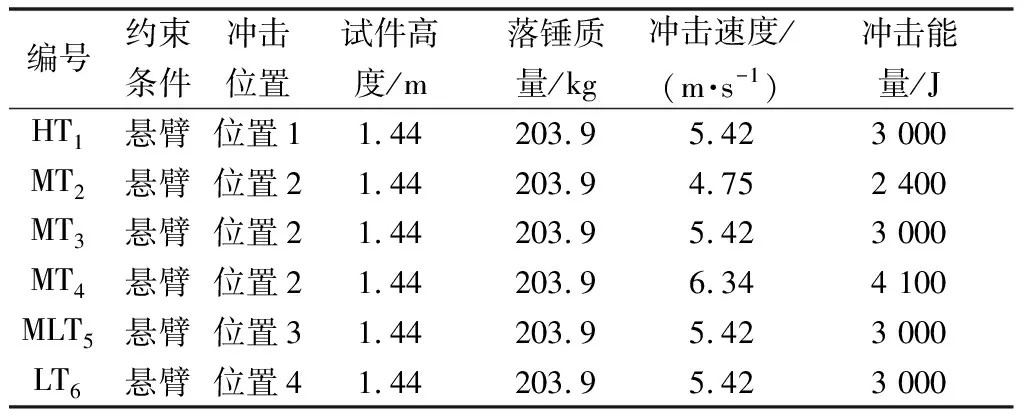
表3 试件基本参数Table 3 Basic parameters of specimens

2.2 破坏形态

图4为不同冲击位置与冲击能量下格构式钢柱的变形特征及破坏形态，由图4可知，各个构件均出现不同程度的屈曲变形，随着冲击能量以及冲击位置的提高，悬臂式钢柱的整体变形情况，有着明显增大的趋势。对于冲击作用在跨中及以上位置(位置1、位置2)的悬臂试件，受冲击部位并未发生明显的局部凹陷，且顶端具有较大侧移率，整体沿钢柱受冲击方向呈斜直线变形;对处于冲击位置3的MLT5构件，虽发生较大侧移，但变形为斜折线状，并以冲击处为折线拐点；而冲击位置4的悬臂试件LT6，受撞处局部屈曲情况严重，冲击点朝两端位置方向，水平侧移不断减小，自由端未发生明显侧移,表现出良好的抗冲击性能。

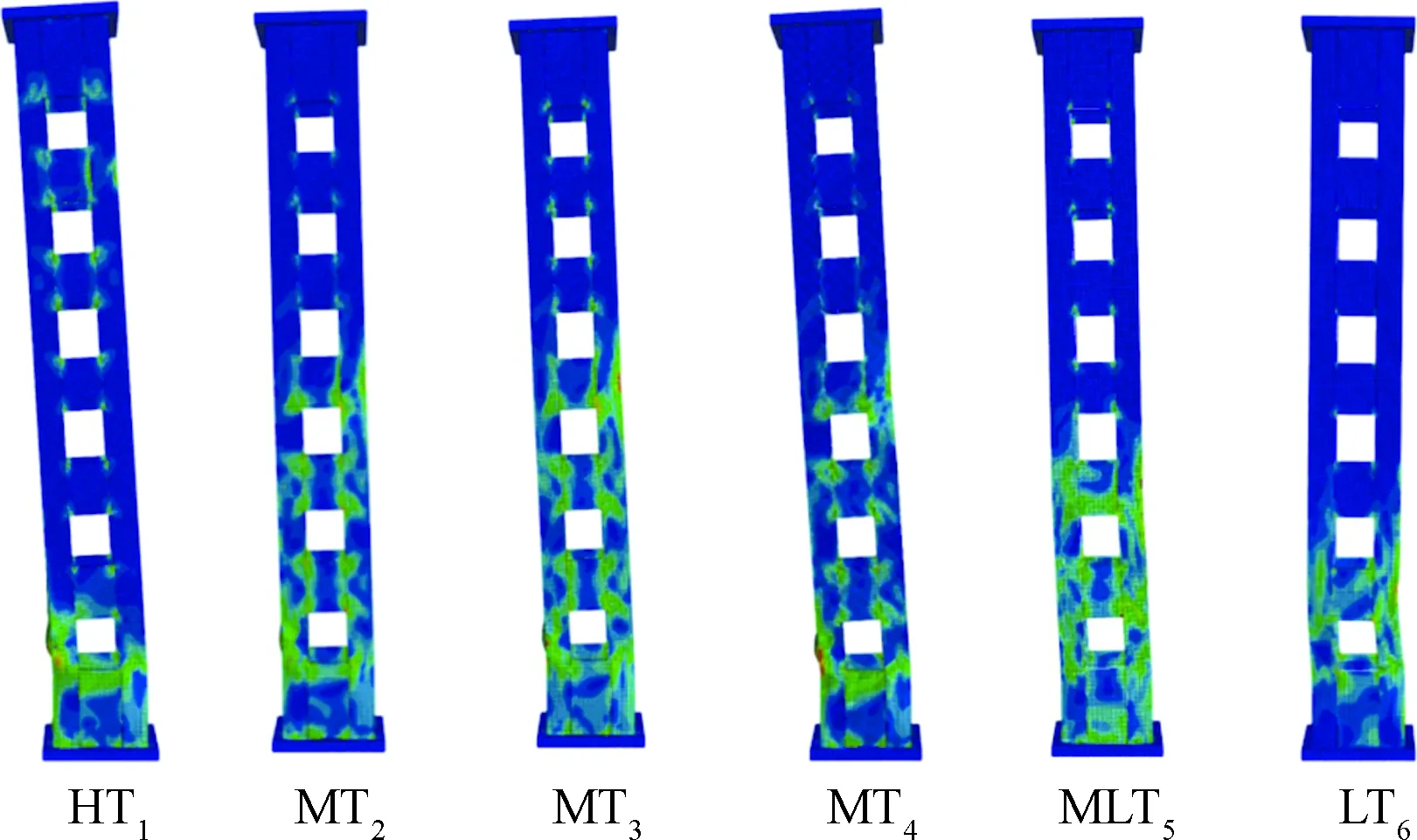
图4 试件整体破坏形态图Fig.4 Global failure patterns charts of specimens

图5为悬臂式钢柱根部典型破坏形态，由图5可知，在对试件跨中进行冲击作用时，悬臂式试件MT4根部缀板处由于弯曲效应大于剪切效应，柱肢受压而产生明显的局部鼓曲现象，而冲击作用在位置4的悬臂式试件LT6，由于冲击位置低，试件根部不易形成塑性铰，破坏时以剪切变形为主。

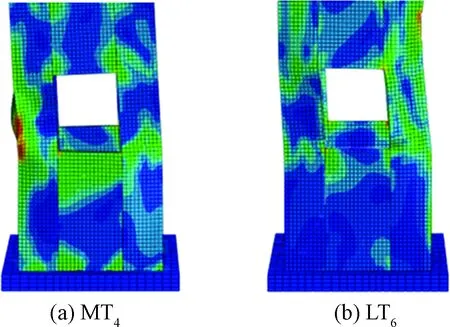
图5 典型柱根部破坏形态Fig.5 Typical local failure patterns of column end

2.3 冲击力时程曲线

图6(a)给出了冲击能量影响下的冲击力时程曲线，随着冲击能量的增加，冲击力趋势基本保持不变，能量大小与冲击力发展无明显影响。悬臂试件在跨中及其以上的位置(位置1、位置2)受到冲击作用时，其冲击力时程曲线大致可以分为四个阶段：峰值段、二值峰值段，平台值段、卸载阶段，由于自由端的约束能力较弱，试件发生变形后发生反弹，与落锤再次接触，进入二次峰值段，该段类似抛物线的时程曲线，且该段的最大值只有最大冲击力峰值的1/4～1/3。当冲击点位置与自由端的距离的缩短时，二次峰值段的最大值增大，该段作用时间提前，持时减小。

图6(b)所示为冲击力位置影响下冲击力时程曲线，可知对于冲击位置较低(位置4)的LT6悬臂试件，因破坏以剪切变形为主，整个冲击过程与两端简支构件类似，均经历了冲击力峰值段、平台值段、卸荷段三个阶段[11]；试件MLT5的与试件LT6相比受到固定端的约束稍弱，冲击力时程曲线发展趋势与冲击点位于跨中及以上位置(位置1、位置2)的悬臂钢柱相似，但并未产生二次峰值段。

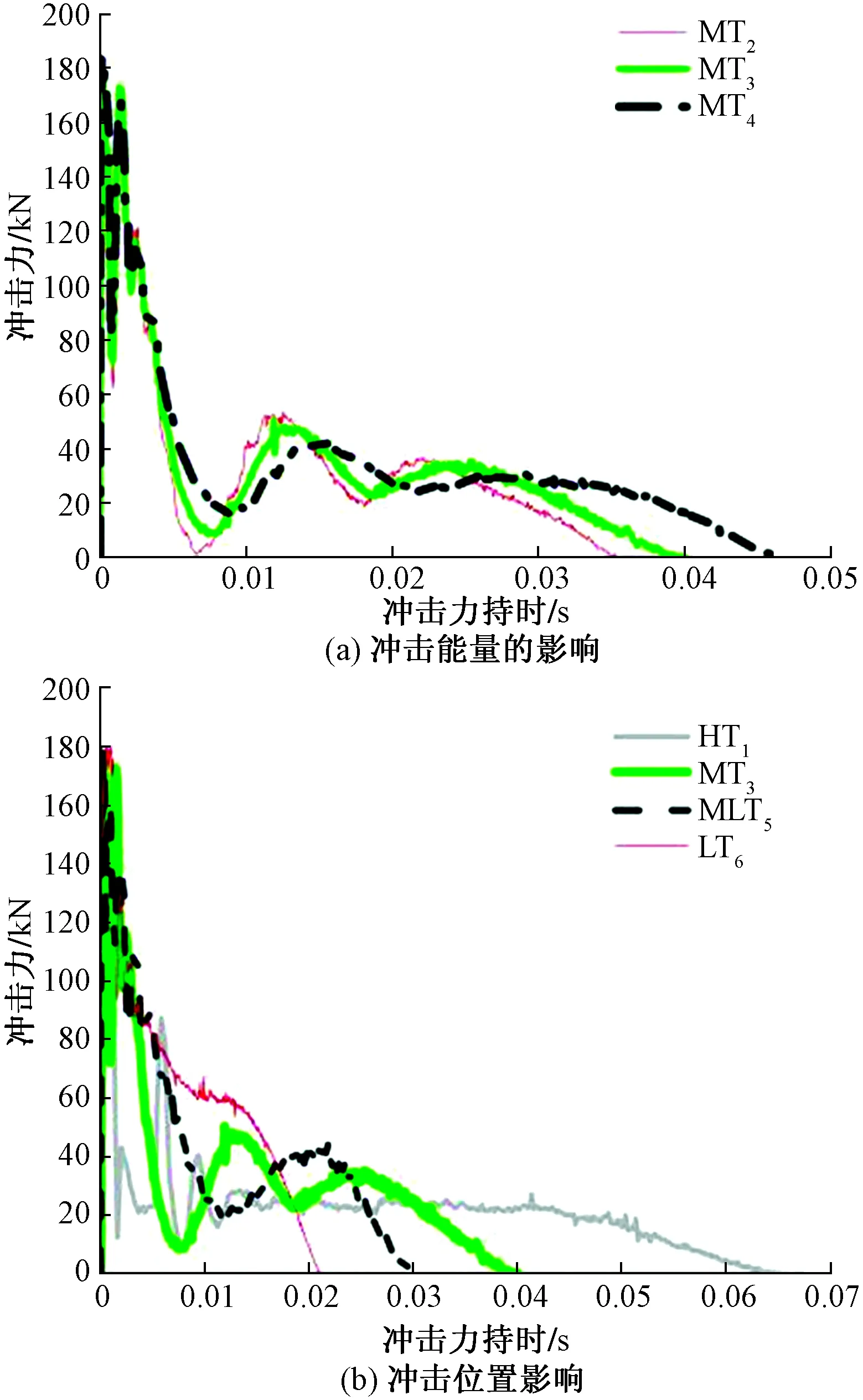
图6 冲击时程曲线Fig.6 Time-history curves of impact force

2.4 影响因素分析

为了更加深入研究冲击荷载作用下钢构件的动态响应情况，从试件的冲击力峰值(Fmax)、冲击力平台值(Fstab)、冲击力持时(Tn)、残余位移(δ)四个方面出发，分析冲击点位、冲击能量对格构式钢柱的动态响应的影响。

2.4.1 冲击位置的影响

图7给出了在不同冲击高度(H)的悬臂试件HT1、MT3、MLT5、LT6动态响应的变化情况，由图7所知，随着冲击作用位置的提高，冲击力峰值变化不大，稳定在 177.37～180.6 kN，可认为冲击位置不对冲击力峰值产生影响。冲击力平台值也作为衡量冲击力大小的重要指标，随着落锤冲击点高度的增加，冲击力平台值依次为60.3、35.04、29.79、23.3 kN，呈现不断减小趋势。冲击力作用时间试件的冲击时间最小为21.06 ms，最大为65 ms，冲击时间随着冲击高度的升高而延长，柱顶残余位移也随冲击高度提高由0.18 mm增长到68.23 mm。由此说明，在作用位置提高的情况下，格构式钢柱所抵御冲击的能力越来越小，通过更大的残余变形进行能量耗散，因而造成更长的作用持续时。

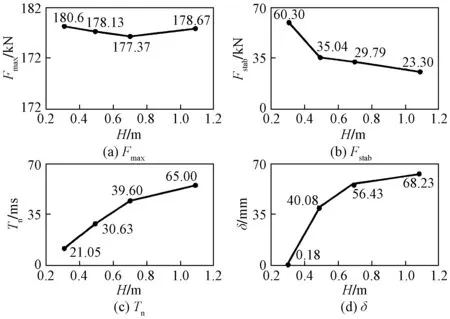
图7 冲击位置的影响Fig.7 Influences of impact position

为了进一步分析落锤作用位置对构件动力响应的作用情况，根据文献[2]中有关冲击力与静力的理论关系对格构式钢柱的抗冲击能力进行分析。

Feq,1=RFu

(1)

式(1)中：Feq,1为构件的理论等效抗冲击承载；R为动力放大系数，由有限元模拟确定，当试件的材料尺寸等情况相同时，R为恒定值；Fu为根据静态分析构件的抗冲击承载力。

荷载的冲击为动态过程，其中冲击力可由实际等效冲击承载力近似表示为

Feq,2=Ea/δ

(2)

式(2)中：Ea为整个冲击作用下构件吸收的能量；δ为冲击位置的残余变形量。

对于构件的静态承载力，由于型钢的塑性性能优异，在受极限荷载时，构件会产生塑性铰从而形成破坏机构，机构的受力情况如图8所示，从格构式构件受弯承载力Mu出发来确定静态下抗冲击承载力为

Fu=Mu/L

(3)

Mu=γWnf

(4)

式中：Mu为试件静态抗弯承载力，通过规范GB 50017—2017[14]得出；L为冲击点距塑性铰的距离，由于底部缀板位置刚度较大，L从底部长缀板顶端处算起；γ为截面塑性发展系数，查表知γ=1；Wn为净截面模量根据截面惯性矩确定；f为钢材的抗拉强度，根据文献[14]知f=266.88 N/mm。

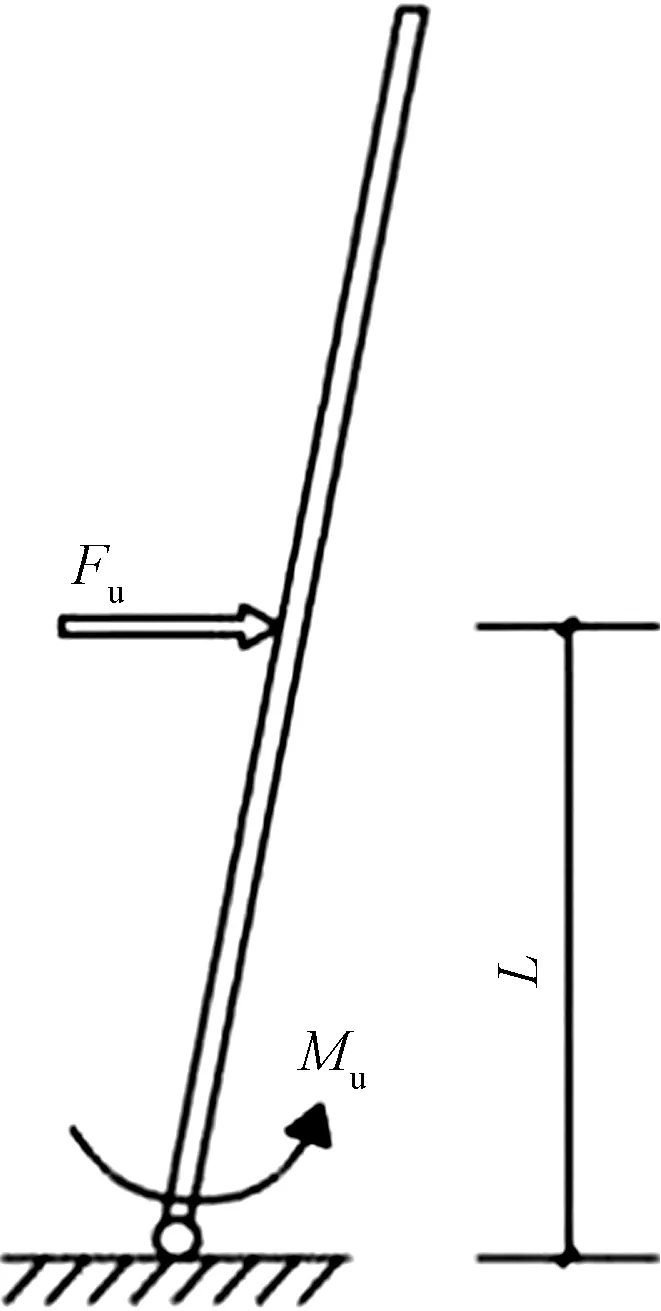
图8 机构的简化模型Fig. 8 Simplified model of failed member

将式(1)与式(3)合并得

Feq,1=RMu/L

(5)

式(5)表明试件抗弯承载力对抗冲击能力的影响关系。计算得受弯承载力Mu=34.04 kN·m，并根据式(1)求得格构式钢柱的动力放大系数R，具体的计算值如表4所示,为保证安全性，R取最小值1.563。

根据式(5)可得出试件的理论等效抗冲击抵承载力与位置关系的曲线，并根据式(2)计算出试件HT1、MT3、MLT5的实际等效抗冲击承载力，由图9可知，两者拟合良好，当冲击位置较高时，试件抗冲击变形能力较差，但随着冲击位置下降，冲击抵抗力不断提高，且提高幅度持续加大。但值得注意的是，对于试件LT6，其冲击能量约3 000 J，吸收能量为2 716.32 J，塑性铰距离L=0.15 m，冲击处残余变形δ=9.52 mm，计算求出的理论等效抗冲击承载力Feq,1应为345.67 kN，但实际的等效抗冲击力Feq,2仅为285.33 kN，差值达69.34 kN之多。这是因为当作用位置较低时，由弯曲效应得出的等效抗冲击承载力较大，在冲击力保持不变的情况下，不易产生塑性铰，此时试件变形破坏由抗剪能力决定，其理论等效冲击承载力为

Feq,1=RVu

(6)

式(6)中：Vu为试件静力分析下的抗剪承载力。

由于目前未发现针对格构式构件抗剪承载力的计算公式，根据材料力学对格构式钢柱静态抗剪承载力进行简化计算，当落锤对试件LT6冲击时，作用截面如图10所示，设冲击作用方向为y方向，由上文可知缀板与角钢抗拉强度相近且采用满焊连接，整体性较好，其抗剪能力主要由格构式钢柱y方向两个狭长矩形部分承担，根据矩形截面切应力强度理论得

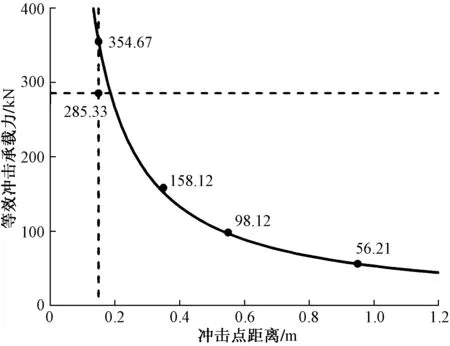
图9 等效冲击承载力Fig.9 Equivalent anti-impact capacity

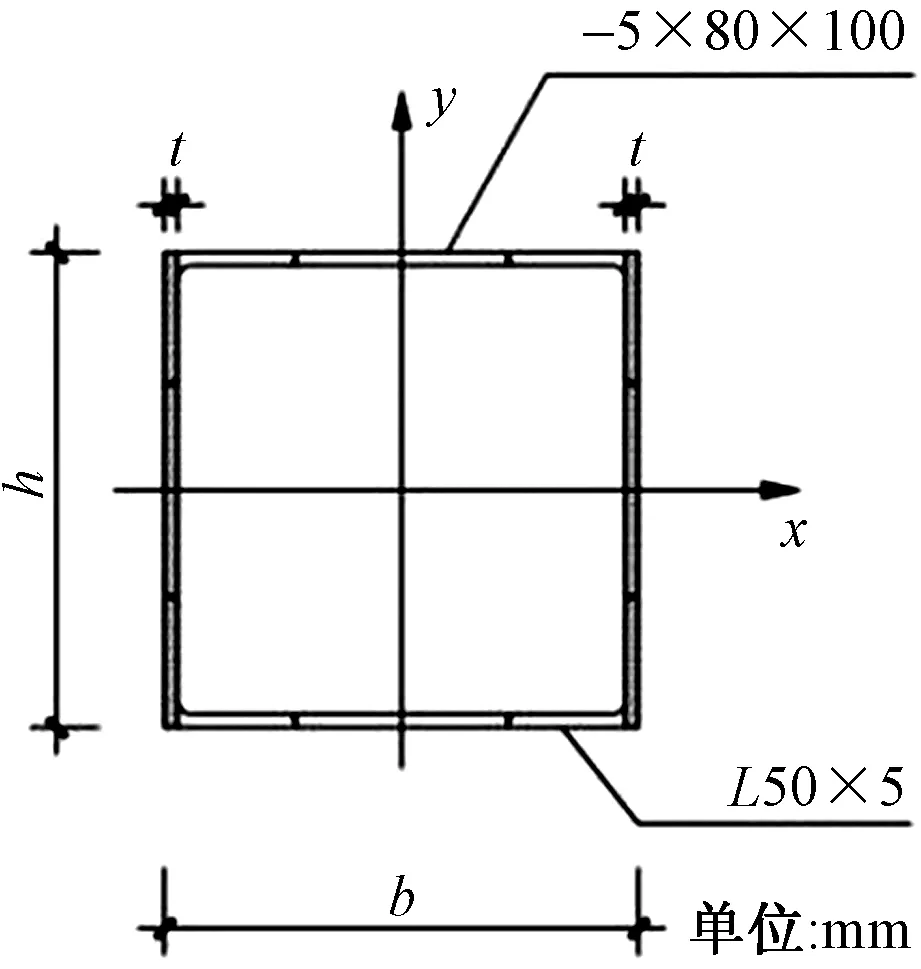
图10 冲击截面Fig.10 Cross section of the specimens under impacts

表4 基于有限元模型R的计算值Table 4 Calculation values of R based on finite element models

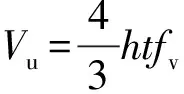
(7)

式(7)中：h为试件截面高度;t为角钢与缀板厚度;fv为材料抗剪强度，由材料力学第四强度理论fv=0.58f，得出fv=154.79 kN。

计算静态抗剪承载力Vu=185.75 kN，得出理论等效抗冲击承载力为Feq,1=RVu=290.32 kN，与实际等效冲击承载了Feq,2=285.33 kN相比,两者误差仅1.7%，证明了计算准确性，并将式(7)拟合，得出悬臂式钢柱在不同冲击位置下抗冲击承载力计算方法。

在本文研究范围内，随着悬臂构件冲击高度下移，试件的抗冲击承载力加速提高，等效抗冲击承载力为

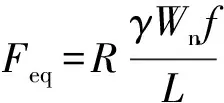
(8)

耐撞性由试件抗弯能力决定，钢柱根部由于弯曲作用屈曲；当冲击点下降至较低位置

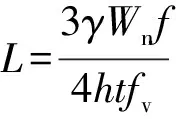
(9)

Mu=Vu，耐撞性由抗剪能力决定，等效抗冲击承载力为

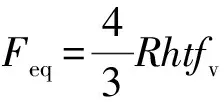
(10)

2.4.2 冲击能量的影响

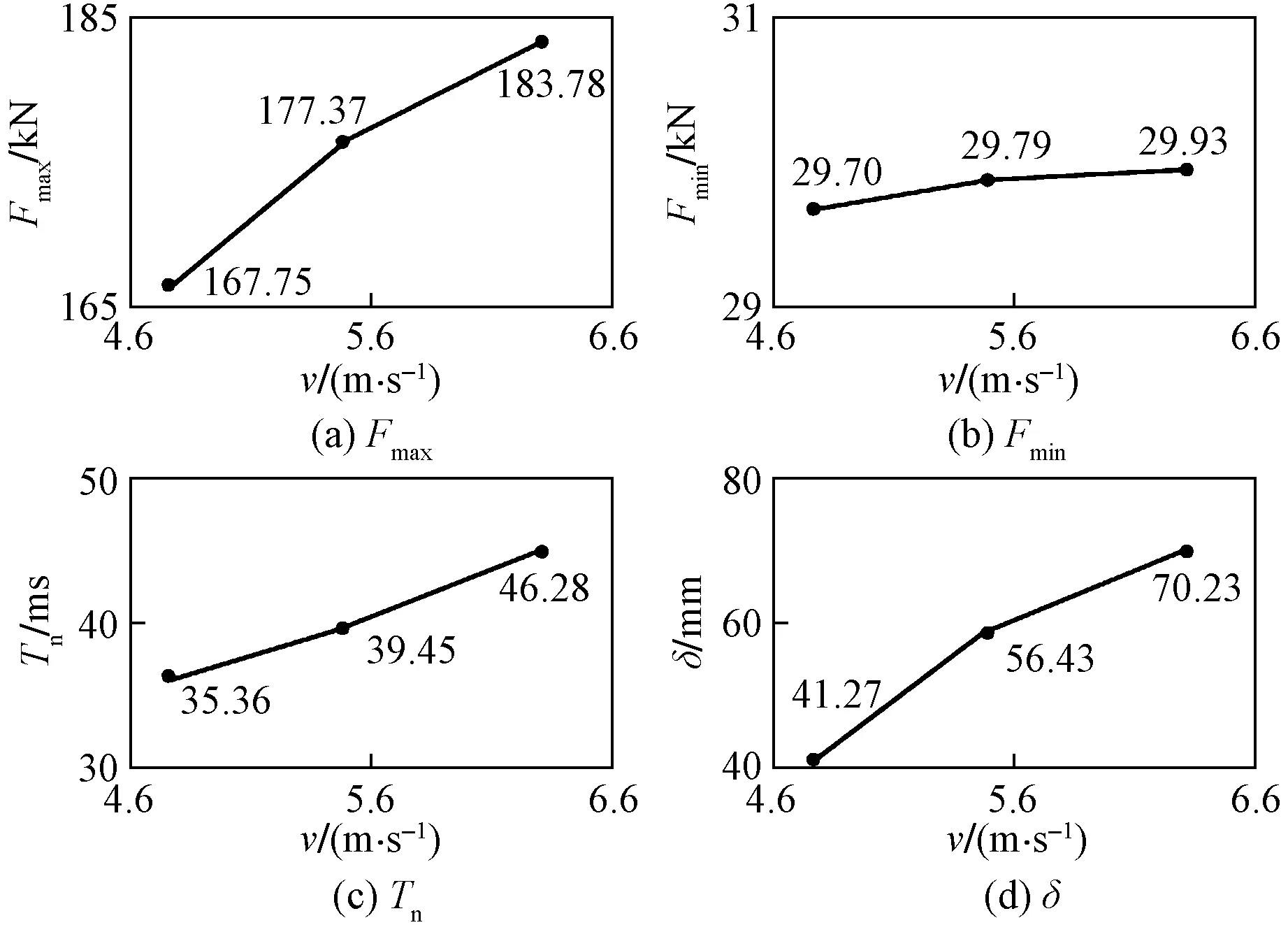
图11 冲击速度的影响Fig.11 Influences of impact velocity

通过控制速度来研究冲击能量对格构式钢柱动态响应的影响，如图11所示，对于尺寸与材料性质相同悬臂式的构件MT2、MT3、MT4，冲击力峰值最小值为167.75 kN,最大值为183.78 kN,随冲击速度增加峰值呈增长趋势。冲击力平台值变化不大，稳定在29.7～29.93 kN。随着冲击速度增长，冲击力持时分别为35.36、39.45、46.28 ms，残余位移分别为41.27、56.42、70.23 mm，冲击持时与残余位移均出现明显的增加。由此可知，随着落锤下落速度的加大，格构式钢柱受到的冲击能量越大，冲击力峰值越高，冲击力平台值基变化不明显，格构式钢柱通过产生更大变形来抵御落锤的冲击作用，这与崔娟玲等[11]对不同冲击速度下的格构式柱的动态响应结论相一致，证明了模拟试验的有效性。