CF3I混合气体比例及放电参数分析

2020-04-10周宇洋何柏娜姜仁卓毛亚哲王乐淼颉雅迪

科学技术与工程 2020年4期

周宇洋，何柏娜，姜仁卓，毛亚哲，王乐淼，颉雅迪

(山东理工大学电气与电子工程学院，淄博 255000)

SF6是电力系统中应用最广泛的气体绝缘介质之一，但SF6是一种具有较大危害的温室气体，其温室效应潜在值是CO2的23 900倍，《京都议定书》将SF6气体列为六种限制温室气体之一[1]。

为寻求环保的替代气体，国内外学者进行了大量的研究，研究内容包括常规气体[2-3]、SF6混合气体[4-6]、电负性气体[7-9]。但目前没有综合性能优于SF6的气体。

CF3I气体无色无嗅，不易燃烧爆炸，不易与其它物质反应，可溶于变压器油，温室效应潜在值极低，且拥有较好的绝缘能力[10-11]，具有良好的研究前景。但CF3I容易液化(251 K，0.1 MPa)[12]，纯CF3I难以在高气压电气设备中直接应用，需要与高液化温度且具有一定绝缘能力的气体混合使用。

因CF3I气体有较好的理化性能，因此近年来国内外学者对CF3I展开了大量研究。Katagiri等[10]、Chen等[11]通过击穿实验研究了CF3I及CF3I-CO2气体的绝缘能力及分解特性。De Urquijo等[13]通过Townsend脉冲实验计算了CF3I及CF3I-N2气体的部分电子运输参数及折合击穿场强。赵谡等[14]对CF3I-N2及CF3I-CO2混合气体的协同效应进行了研究。徐玲铃等[15]对三元CF3I混合气体协同效应进行了理论计算。赵虎等[16]对300 K下CF3I-N2及CF3I-CO2混合气体的绝缘性能进行了理论计算。

虽然目前已有部分对CF3I混合气体的实验或理论研究，但基本是对所有比例范围的CF3I混合气体进行的研究，并未考虑所研究范围内混合气体实际工况下的可行性，且研究内容多为绝缘能力或协同效应等宏观量，并未对电子运输参数等中间微观量进行深入细致的分析。基于此，本文根据实际工况条件首先确定有效的CF3I混合气体比例范围，并对范围内的CF3I放电参数进行深入理论研究，为CF3I在电气设备中的应用奠定理论基础。

1 CF3I混合气体比例分析

CF4、N2、CO2气体有较好的理化性质，常被作为缓冲气体使用[5-8]，故引入此三种气体作为本文的CF3I缓冲气体进行研究。在混合气体中，最易发生液化的气体成分决定了整体的液化条件。CF4、N2、CO2气体的液化温度都较低且远小于CF3I气体，因此CF3I决定了其混合气体的液化条件。

气体液化条件取决于压力和温度，可用气体饱和蒸气压方程定量描述。因此求解CF3I气体饱和蒸气压方程即可定量求解混合气体液化条件，CF3I气体的饱和蒸气压方程[12]如式(1)所示：

lnP/Pc=(A1f+A2f1.25+A3f3+A4f7)(TC/T)

(1)

式(1)中：P为CF3I气体液化压力，MPa；Pc为CF3I气体临界压力，Pc=3.953 MPa；f=1-T/Tc；Tc为CF3I气体临界温度，Tc=396.44 K；T为气体液化温度，K；A1=-7.204 825；A2=1.393 833；A3=-1.568 372；A4=-5.776 90。

道尔顿定律指出，理想气体混合物的总压力等于其中各气体成分压力之和，公式为

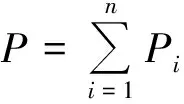
(2)

式(2)中：P为混合气体的总压力，MPa；Pi为混合气体中第i种成分的分压力，MPa。

将混合气体视为理想气体并根据CF3I气体的饱和蒸汽压方程及道尔顿分压定律即可近似计算出CF3I各种比例及压力下的液化温度。

在气体绝缘设备中，为保证绝缘气体的绝缘及灭弧能力，断路器中的气体压力一般大于0.3 MPa，故将几种气体断路器中常见的气压代入式(1)、式(2)计算不同CF3I气体比例下的液化温度，结果如表1所示。

表1 CF3I混合气体在一定气压下的液化温度Table 1 Liquefaction temperature of CF3I mixed gas at a certain pressure

若将251 K(纯CF3I气体在0.1 MPa的液化温度)设为混合气体最低工作温度，则由表1可知：在CF3I掺入比例小于等于15%的情况下，混合气体可在0.6 MPa的气压保持气态；CF3I掺入比例30%时，混合气体仅能在压力0.3 MPa维持气态。因此在CF3I混合气体中，较低的CF3I比例可使混合气体在更高的压力下维持气态。在设置的最低工作温度条件下，CF3I的比例最高不应高于30%。在高压力的条件下混合气体的CF3I比例应降低，否则混合气体的工作温度条件会难以满足，在应用中可能出现液化现象。因此将30%作为混合气体的CF3I比例上限进行Boltzmann计算研究。

2 Boltzmann计算原理

Boltzmann方程是利用待求气体的多种碰撞截面的微观量求解气体宏观量的数学工具。求解Boltzmann方程可得出待求气体放电过程中的电子运输及能量分布参数，进而可解出待求气体的绝缘性能。通过求解Boltzmann方程可得到气体的电子能量分布函数(electron energy distribution function, EEDF)，并可进一步求解得到折合电离系数(α/N)及折合吸附系数(η/N)，并以此得到气体的折合临界击穿场强(E/N)cr。其中α为电离系数，η为吸附系数，E为电场强度，N为气体粒子数密度。

求解方程有多项或两项近似的方法。在电场各向异性较小，弹性碰撞截面远大于非弹性碰撞截面的情况下两项近似的方法精度高并且具有较高的可靠性。使用软件BOLSIG+对两项近似Boltzmann方程进行求解，并设求解温度300 K，电子速度沿电场方向呈轴对称分布，电场各处电子碰撞概率相同，碰撞电离后电子能量平分。

求解Boltzmann方程需要气体的碰撞截面数据作为条件。从LXCat数据库选取了认可度较高的碰撞截面数据，包括SF6[17]、CF3I[18]、CF4[19]、N2[20]、CO2[21]，并与文献[14-16]中的碰撞截面选取及计算结果进行了比对，验证了碰撞截面选择的可靠性。

3 计算结果及分析

3.1 CF3I混合气体的 EEDF

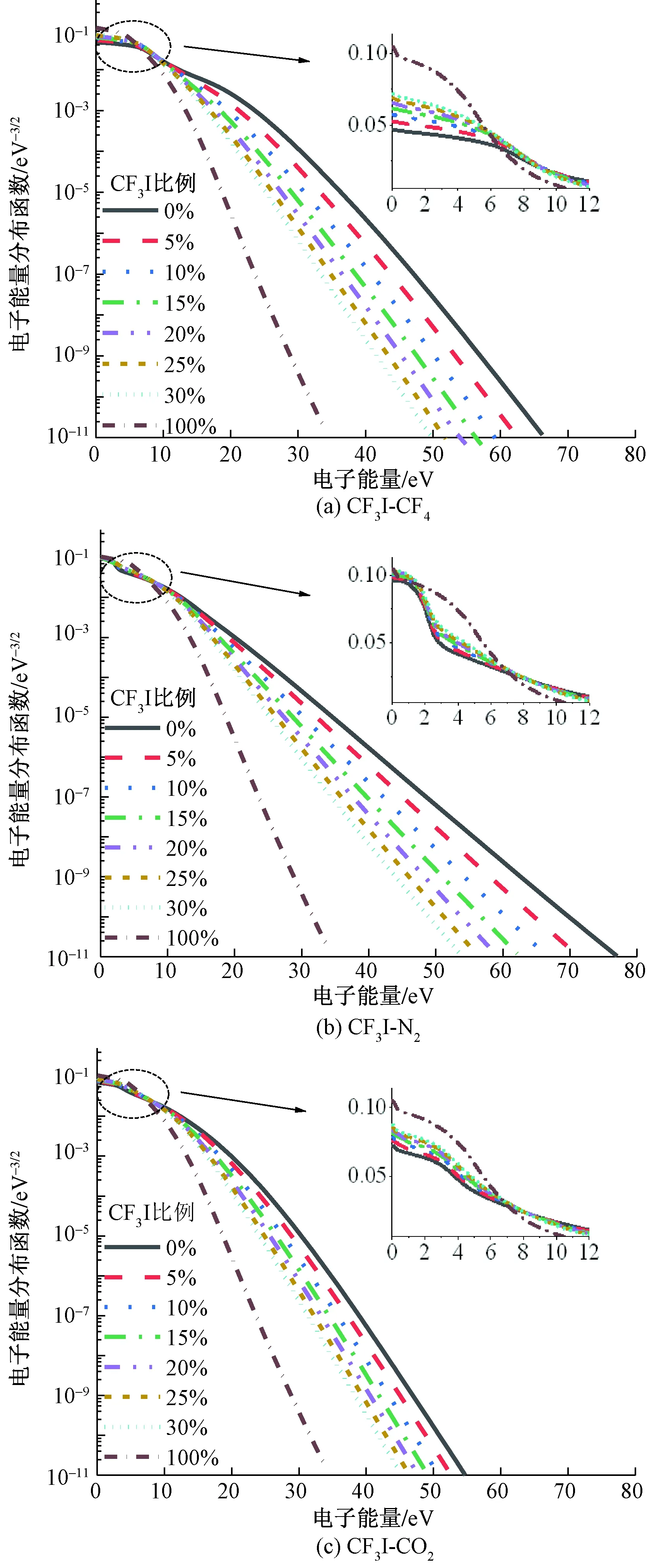
图1 三种 CF3I混合气体在不同比例下的EEDFFig.1 EEDF of three CF3I mixed gases at different incorporation ratios

图1为折合电场强度E/N为300 Td(1 Td=10-21V·m2)时三种不同比例混合气体的EEDF，EEDF反映气体中各个能级的电子密度。由图1可知，在电子能量较低区域(<7 eV)，EEDF随着CF3I比例的增加而增加，而在较高电子能量区域(>7 eV)的EEDF随CF3I掺入比例的增加而减少。因为电负性气体CF3I，可有效捕获自由行程中的电子，从而减少了高能电子的数量并增加了低能电子的数量，故CF3I可抑制电子获取更高的能量且抑制效果与CF3I比例呈正相关。

由图1(b)可知，CF3I-N2混合气体的EEDF 在电子能量1.5～3 eV时骤降，降低程度与N2比例正相关，且CF3I-N2混合气体在0.5～1.5 eV的范围内EEDF较高，在图1(a)、图1(c)中不存在该现象，因为N2在1.5～3 eV时振动激发碰撞降低了电子能量，使该范围内低能电子增加高能电子减少。图1(c)中，EEDF曲线尾部高能区的电子能量小于另两种混合气体，表明CF3I-CO2混合气体对高能电子的抑制作用最优。对EEDF进一步求解得到α/N及η/N。

3.2 CF3I混合气体的α/N及η/N

α/N表示单位分子密度下气体分子的电离频率，表征气体电离出电子的能力。三种CF3I混合气体的α/N如图2所示。

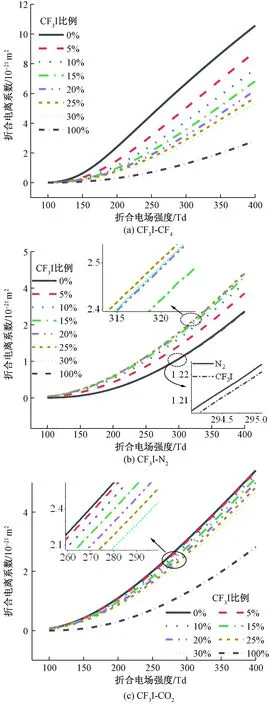
图2 三种 CF3I混合气体在不同比例下的α/NFig.2 α/N of three CF3I mixed gases at different incorporation ratios

如图2(a)、图2(c)，E/N一定时，α/N随CF3I含量的增加而减小，表明增加CF3I比例会削弱CF3I-CF4及CF3I-CO2的电离频率。如图2(b)，因CF3I与N2的电离碰撞截面近似，所以纯CF3I气体与纯N2的α/N曲线近似相等。E/N一定时，CF3I-N2混合气体的α/N随CF3I比例的增加先增大后减小。对比图3(a)～图3(c)可发现，当混合比一定时，α/N随E/N增大而增大，表明增大E/N能够促进电离反应。且在CF3I 比例及E/N相同时，CF3I-CF4混合气体的α/N明显大于CF3I-N2及CF3I-CO2混合气体，表明CF3I-CF4混合气体在相同条件下电离反应率最高。

η/N表示单位分子密度下气体分子的吸附频率，表征混合气体吸附电子的能力。三种CF3I混合气体的η/N如图3所示。

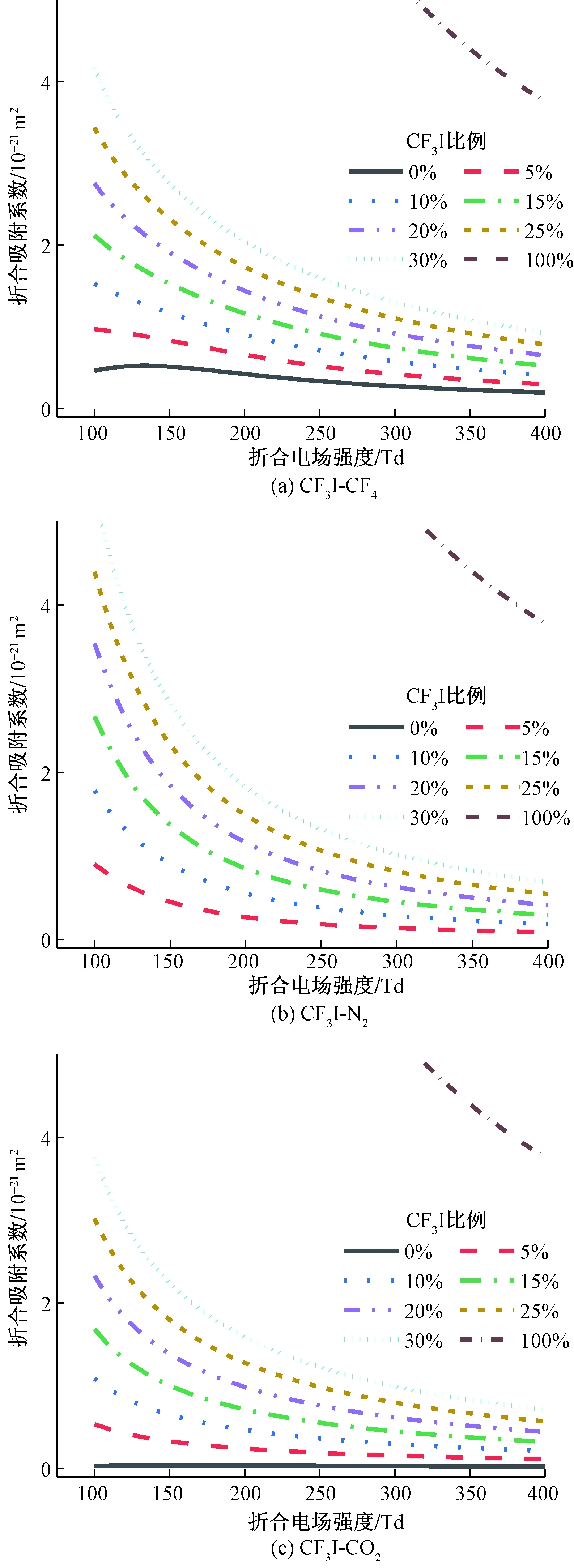
图3 三种CF3I混合气体在不同比例下的η/NFig.3 η/N of three CF3I mixed gases at different incorporation ratios

由图3可知，纯CF3I气体的η/N远大于三种混合气体及缓冲气体，且当混合比一定时，三种混合气体的η/N均随E/N的增大而减小，E/N<200 Td时，η/N曲线非线性程度较高，表明低场强时η/N对电场变化的敏感度较高。当E/N一定时，三种气体的η/N均随CF3I含量的增加而增大，表明CF3I捕获电子的能力较强，增大了混合气体的η/N。因N2不存在吸附截面，CO2吸附截面较小，弱电负性气体CF4存在一定的吸附截面，因此在相同比例下CF3I-N2及CF3I-CO2混合气体的η/N较为相近，相同比例的CF3I-CF4混合气体η/N在E/N>200 Td时略高于另外两种混合气体。因此CF3I-CF4混合气体的吸附特性要优于另外两种气体。通过α/N及η/N可求得气体的折合有效电离系数(α-η)/N。

3.3 CF3I混合气体的(α-η)/N及(E/N)cr

(α-η)/N反映气体电离反应和吸附反应的强弱情况。吸附反应强于电离反应时(α-η)/N<0，反之，(α-η)/N>0。(α-η)/N=0表示碰撞电离过程与碰撞吸附过程处于平衡状态。三种CF3I混合气体的(α-η)/N如图4所示。

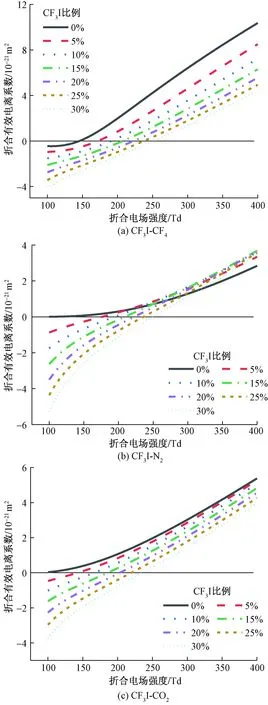
图4 三种CF3I混合气体在不同比例下的(α-η)/NFig.4 (α-η)/N of three CF3I mixed gases at different incorporation ratios

由图4可知，(α-η)/N随E/N的增大而增大。当E/N一定时，三种混合气体的(α-η)/N随着CF3I比例的增加而减小，表示CF3I比例的增加降低了混合气体的有效电离频率。E/N=400 Td时，所有比例下的CF3I-CF4混合气体(α-η)/N均大于等比例的另外两种混合气体，表示在E/N较高时，CF3I-CF4混合气体有效电离反应强于另外两种混合气体，会电离出更多自由电子。

在(α-η)/N=0时，气体处于临界击穿状态，此时(α-η)/N曲线的一阶导数c可表征气体绝缘能力对电场变化的敏感程度，c越小表示电场均匀程度对气体绝缘特性的影响越低，其值如表2所示。

由表2可知，c随缓冲气体比例的增加而减小，三种混合气体的c均小于SF6的29 kV-1[22]，其中CF3I-N2及CF3I-CO2混合气体c更低，表明CF3I-N2及CF3I-CO2混合气体在不均匀电场条件下电气性能优于CF3I-CF4混合气体及SF6，且电场均匀度对其绝缘特性的影响相对较小。

气体临界击穿状态下对应的E/N即气体的折合临界击穿场强(E/N)cr，表征气体的绝缘能力。不同比例下三种CF3I混合气体及根据碰撞截面得到的SF6气体的(E/N)cr如图5所示。

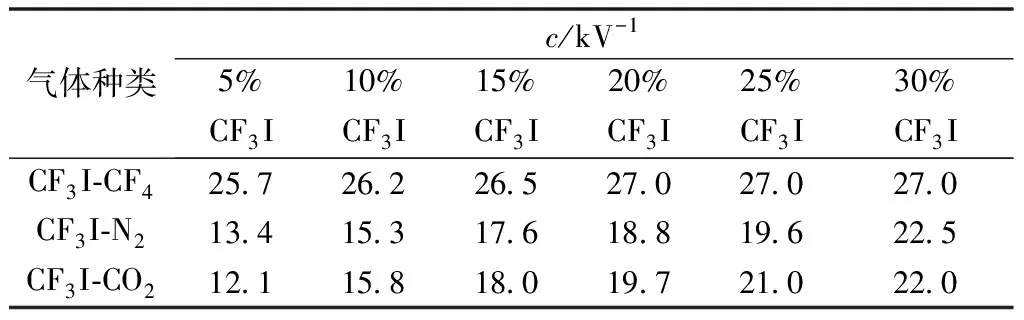
表2 CF3I混合气体的cTable 2 The c of CF3I mixed gas

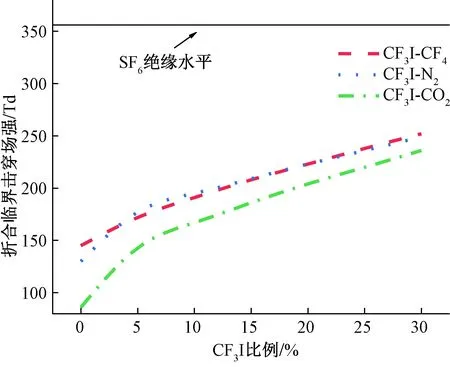
图5 SF6及三种CF3I混合气体在不同比例下的(E/N)crFig.5 (E/N)cr of SF6 and three CF3I mixed gases at different incorporation ratios

如图5，三种混合气体的(E/N)cr均与CF3I比例正相关。在CF3I比例较低时，CF3I-CO2混合气体的(E/N)cr明显随CF3I比例非线性增加，CF3I-N2混合气体的(E/N)cr非线性程度较低，CF3I-CF4混合气体的(E/N)cr线性程度较高，在CF3I比例较高时，三种混合气体的(E/N)cr均随CF3I比例线性增加。CF3I-CF4及CF3I-N2混合气体的(E/N)cr数值相近，并大于CF3I-CO2混合气体。

3.4 CF3I混合气体的协同效应

混合气体的(E/N)cr随气体比例的非线性变化的现象表示混合气体的(E/N)cr不同于各气体组分单独作用的总和，称为气体的协同效应。协同效应可用协同效应系数ξ表征，ξ越大，协同效应越强。计算公式如式(3)所示。

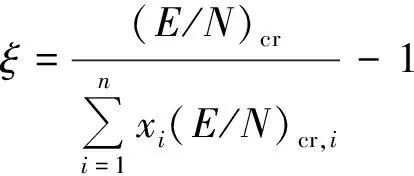
(3)

式(3)中:(E/N)cr为待求混合气体的(E/N)cr，Td；xi为第i种气体所占气体总量的比例，%；(E/N)cr,i为第i种气体的(E/N)cr，Td。三种混合气体的ξ如图6所示。

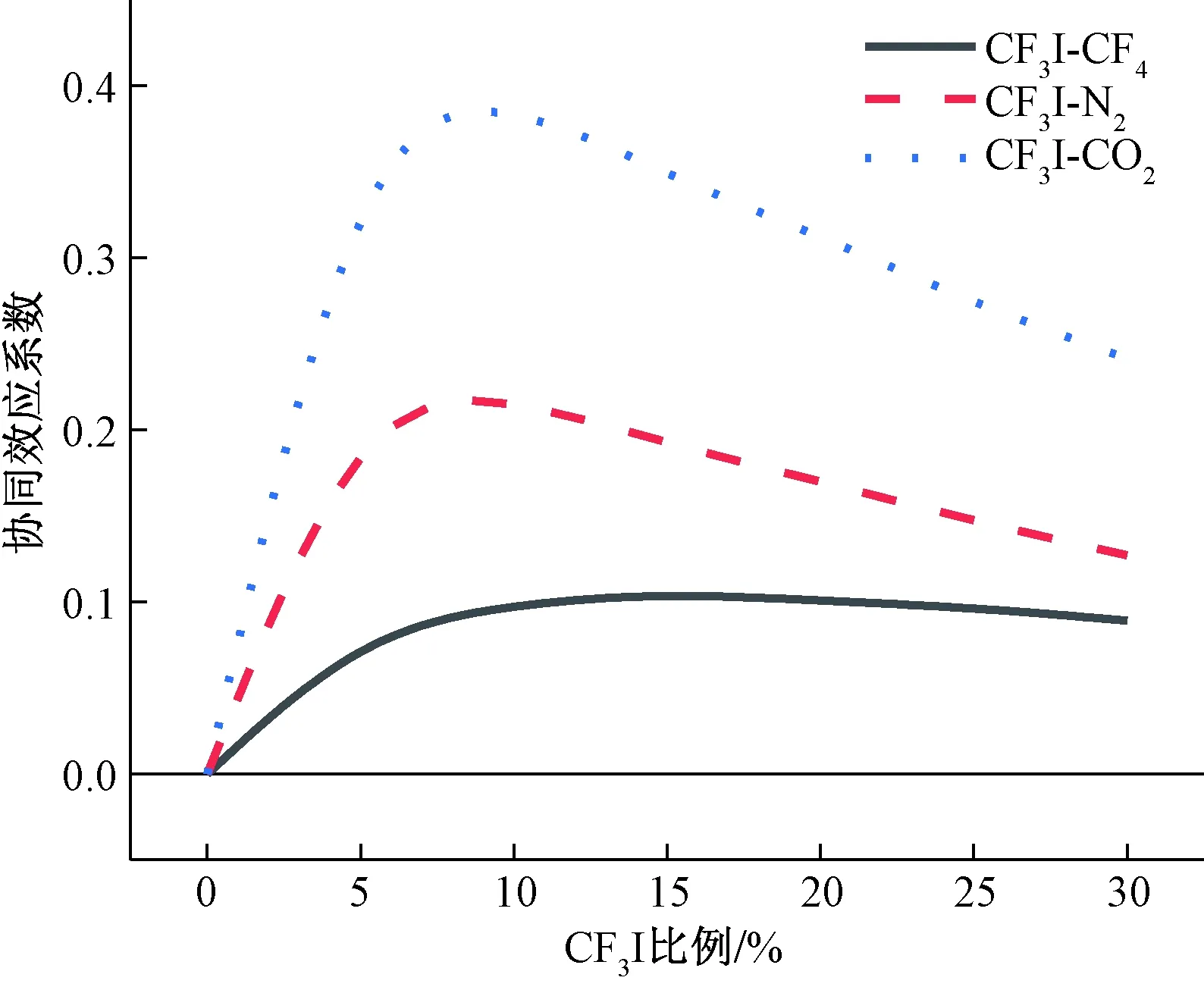
图6 三种CF3I混合气体在不同比例下的协同效应系数Fig.6 Synergistic effect coefficient of three CF3I mixed gases at different incorporation ratios

如图6，三种混合气体的值均大于零，表明三种混合气体均存在正协同效应，即三种混合气体的(E/N)cr均大于其各成分的(E/N)cr加权和。CF3I比例5%～20%时，三种混合气体的值较高，在该比例下协同效应最为显著。且CF3I-CO2混合气体的协同效应高于CF3I-N2混合气体，CF3I-CF4混合气体协同效应最低。

由图5可知，CF3I混合气体的绝缘能力随CF3I比例的增加而增强，但是较高的CF3I比例会导致气体的工作压力及温度受限，使混合气体不能在较高压力或温度条件下使用，在设定的最低工作温度条件下，0.3 MPa时CF3I的混合比例最高只能达到30%，15%及以下 CF3I比例的混合气体则可在0.6 MPa下使用。在CF3I气体比例为30%时，CF3I-CF4、CF3I-N2、CF3I-CO2混合气体分别达到了SF6气体绝缘能力的69.8%、68%及66.3%，CF3I气体比例为15%时，分别为58.4%、58.7%及52.2%，虽然降低CF3I气体比例降低了混合气体的绝缘能力，但由图6可知，在CF3I比例较低的情况下，气体的协同效应更为显著，使CF3I比例下降对混合气体绝缘能力的影响变小，混合气体仍有相对较高的(E/N)cr，并未与CF3I比例的下降而等比例的降低绝缘性能，因此利用气体的协同效应可在较低CF3I气体比例下使混合气体获得相对较强的绝缘性能。

3.5 计算结果验证

为验证碰撞截面的选取与计算结果的可靠性，将文中计算的典型结果(E/N)cr与可信度较高的参考文献值进行对比，如图7所示。

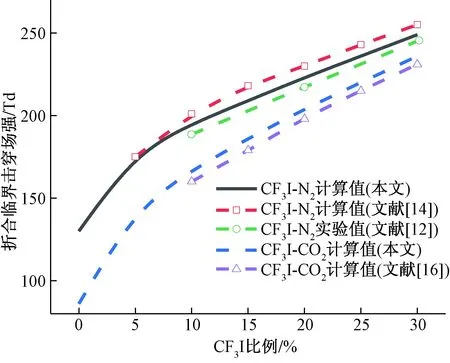
图7 CF3I/N2及CF3I/CO2混合气体(E/N)cr值与文献的对比Fig.7 (E/N)cr of CF3I/N2 and CF3I/CO2 mixed gas compared with literature

由图7可知，计算的CF3I/N2混合气体的(E/N)cr介于文献[14]的计算值与文献[12]的实验值之间；CF3I/CO2混合气体的(E/N)cr略高于文献[16]的计算值，且相差较小。当前对CF3I/CF4混合气体的研究较少，尚无权威参考值，但CF3I/CF4混合气体的研究结果及与其他混合气体的相对大小关系均与文献[15]较为相近。此外所得的另两种混合气体的(E/N)cr相对大小关系也与文献[14-16]一致，因此可认为选择的碰撞截面及计算方法是可靠的。