涉及小代数体函数的Milloux 不等式
2020-04-10祝笑笑刘晓俊
祝笑笑,刘晓俊
(上海理工大学 理学院,上海 200093)
1 问题的提出
定义1[1]代数体函数是由不可约方程

所确定的k值解析函数,其中Aj(z)(j=0,1,···,k)是z的全纯函数,并且不在一点同时为零。特别地,当k=1时,W(z)即为亚纯函数;当Aj(z)(j=0,1,···,k)都是多项式时,W(z)为代数函数。
代数体函数的第二基本定理首先由Valiron 在1929 年提出,后来有很多学者给出了详细的证明。下面定理的形式来自文献[2]。
定理1设W(z)={Wt(z)}是{|z|<R}内由式(1)所确定的k值无重因子代数体函数,并且每个分支Wt(z)不恒为常数值。设at(t=1,2,···,p)是p个不同的复数(有穷或否),则对任意的r∈(0,R),恒有
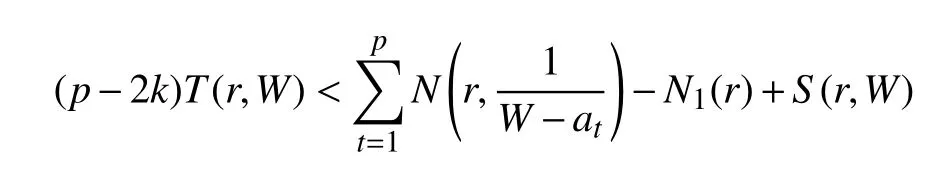
若{at}中不含 ∞,由于N(r,W)≤T(r,W),上式变形成
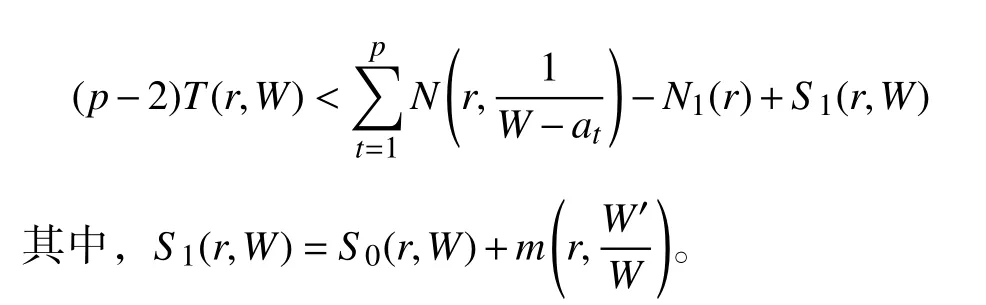
若{at}中含有 ∞,在上式中可令ap+1=∞,则上式可改写成
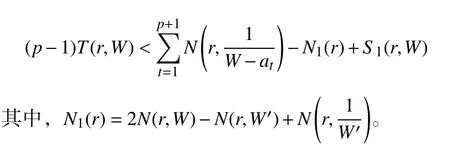
对于亚纯函数的第二基本定理,Yang 等[3]曾给出一个涉及导数的推广,从而得到了亚纯函数的Milloux 不等式[4]。之后,何育赞又给出了代数体函数的Milloux 不等式的一种形式。
定理2[1]设W(z)是k值无重因子代数体函数,并令av(v=1,2,···,p)和bj(j=1,2,···,q)为两组有穷异于零且每组内判别的复数,则有
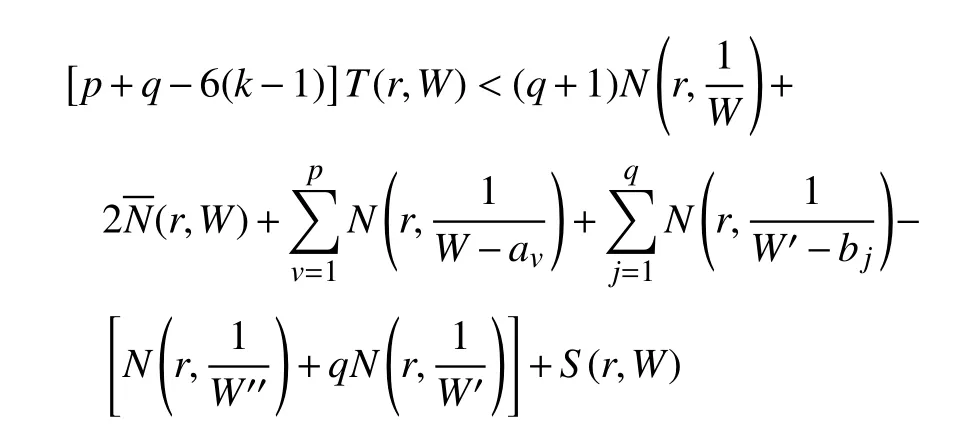
其中,S(r,W)具有余项性质。
定义2[1]设是区域D上的k值广义代数体函数。
a.记W(z)的所有代数体映射之集为YW(D);
b.称广义代数体集合HW(D)={h◦W(z);h∈YW(D)}为W(z)的代数体函数类。
定义3[1]设W(z)是圆盘D={|z|<R}上的k值代数体函数,记W(z)的所有小代数体函数集合为
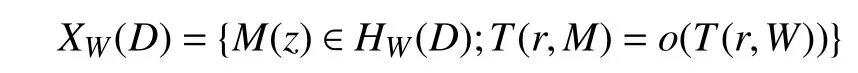
定义4[2]设W(z)为代数体函数,则
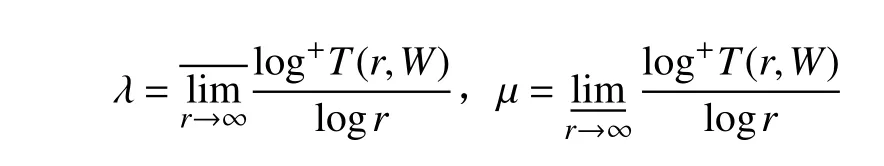
分别称为W(z)的级和下级。
对于代数体函数的第二基本定理,不久前,孙道椿等[1]把这个结果改进为小代数体函数的情形,得到了小代数体函数的第二基本定理。
定理3[1]设W(z)={Wt(z)}是C上非常数的k值无重因子代数体函数,是W(z)的q≥2个不同的小代数体函数(也可能是小亚纯函数及有限或无限的复常数),则对任意的ε∈(0,1)及r>0,恒有
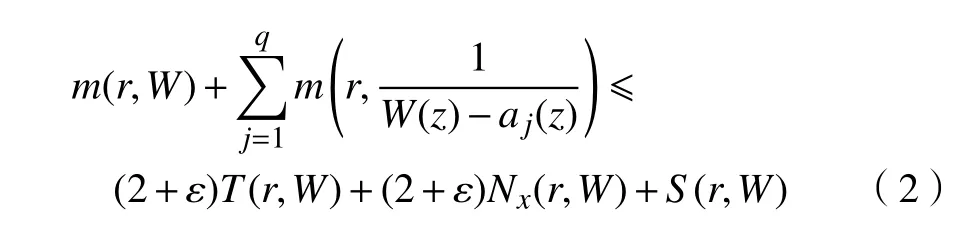
其等价形式为
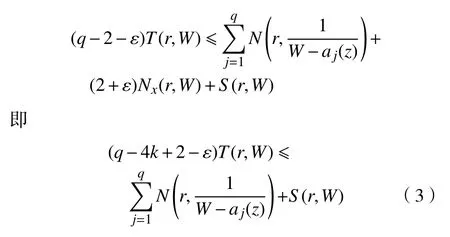
本文主要以定理1 和定理3 为工具,将定理2 的结论改进为涉及小代数体函数的情形,从而得到了下面的结论。
定理4设W(z)是k值无重因子代数体函数,令分别为W(z)和W′(z)的不同的小代数体函数(也可能是小亚纯函数[5]及有限或无限的复常数[6],p,q≥2),则有
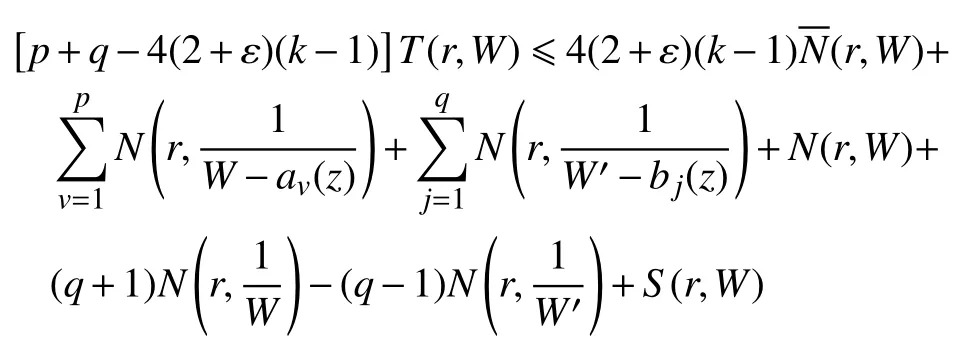
推论设W(z)是由式(1)所确定的k值有穷正级整代数体函数[7],若0,∞,av(z)(v=1,2,···,p)是W(z)的判别有穷的Borel 例外值,bj(z)(j=1,2,···,q)是W′(z)的q个判别有穷的Borel 例外值,且av(z),bj(z)不恒为0 和 ∞,则W(z)为常数。
2 相关引理
引理1[1]设W(z)为k值无重因子代数体函数,则对任意正整数v∈N,它的v阶导数W(v)(z)满足

引理2[4]设W(z)是由式(1)确定的k值代数体函数,则有
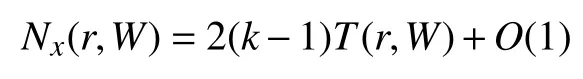
引理3[4]设W(z)为k值无重因子代数体函数,则

类似于亚纯函数,定义代数体函数的Borel 例外值。
定义5[9]设W(z)是由式(1)确定的非常数值的有穷正级k值无重因子代数体函数,若对任意的复数b,有
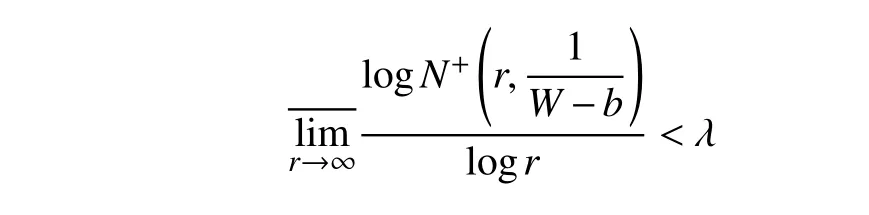
则称b为W(z)的Borel 例外值。
引理4设W(z)是由式(1)确定的非常数值的有穷正级k值无重因子[10]代数体函数,a(z)为W(z)的任意小代数体函数,则
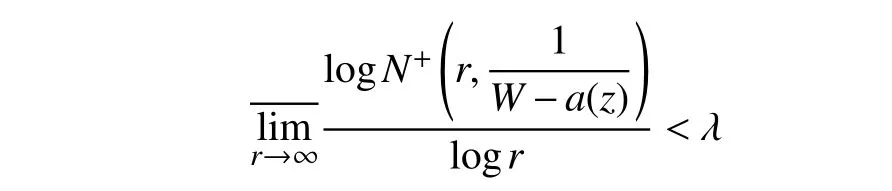
至多有(4k-2)个Borel 例外值[11],其中 λ为W(z)的级。
证明若存在(4k-1)个Bor el 例外值,满足

结合小代数体函数的第二基本定理[12](定理3),并由引理3,得
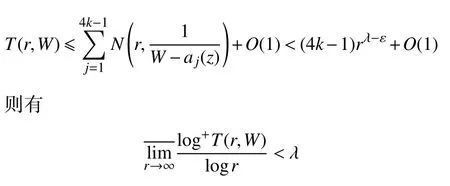
矛盾,证毕。
3 主要结论的证明
定理4 的证明。
对W′(z)和bj(z)(j=1,2,···,q+1)应用定理3 并结合第二基本定理,令bq+1(z)=0,得
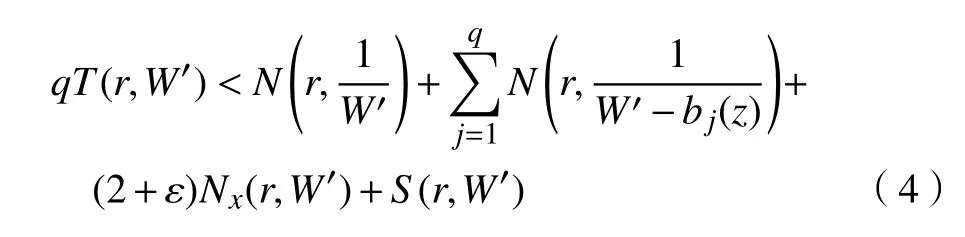
对W(z),av(z)(v=1,2,···,p+1)应用定理3 并结合第二基本定理,并令ap+1(z)=0,得
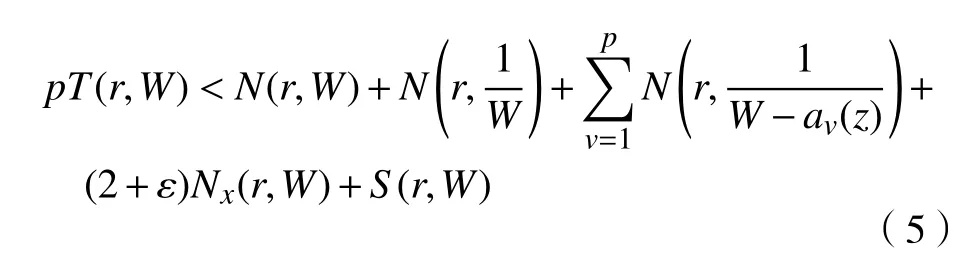
再由Jensen 公式
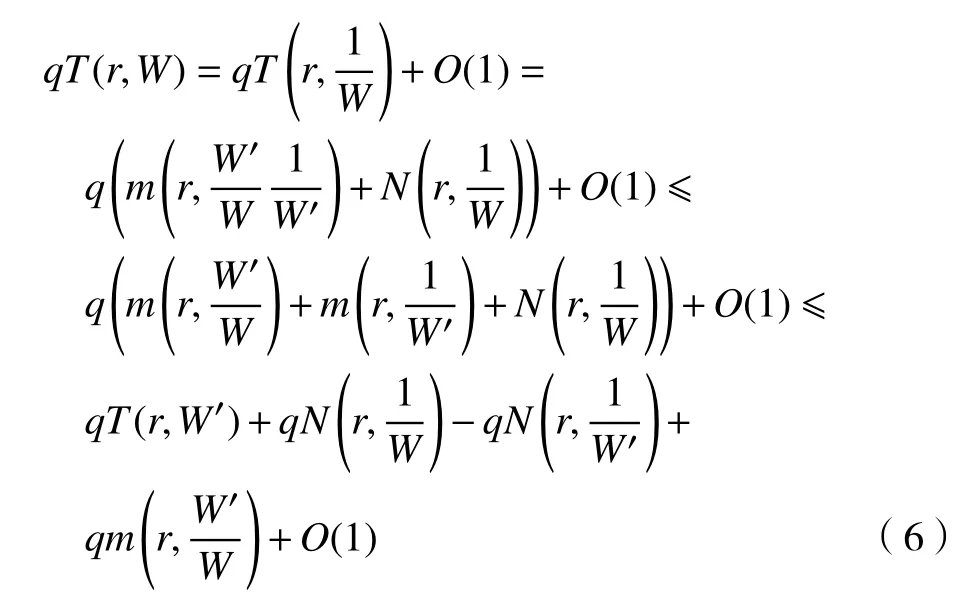
将式(4)应用于式(6),得
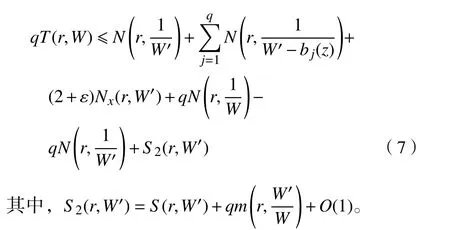
将式(5)与式(7)相加,得
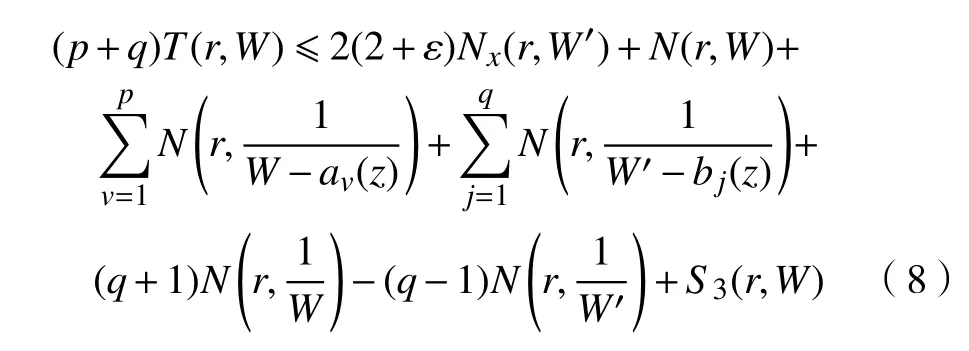
其中,S3(r,W)=S(r,W)+S2(r,W′)。
由引理1 和引理2
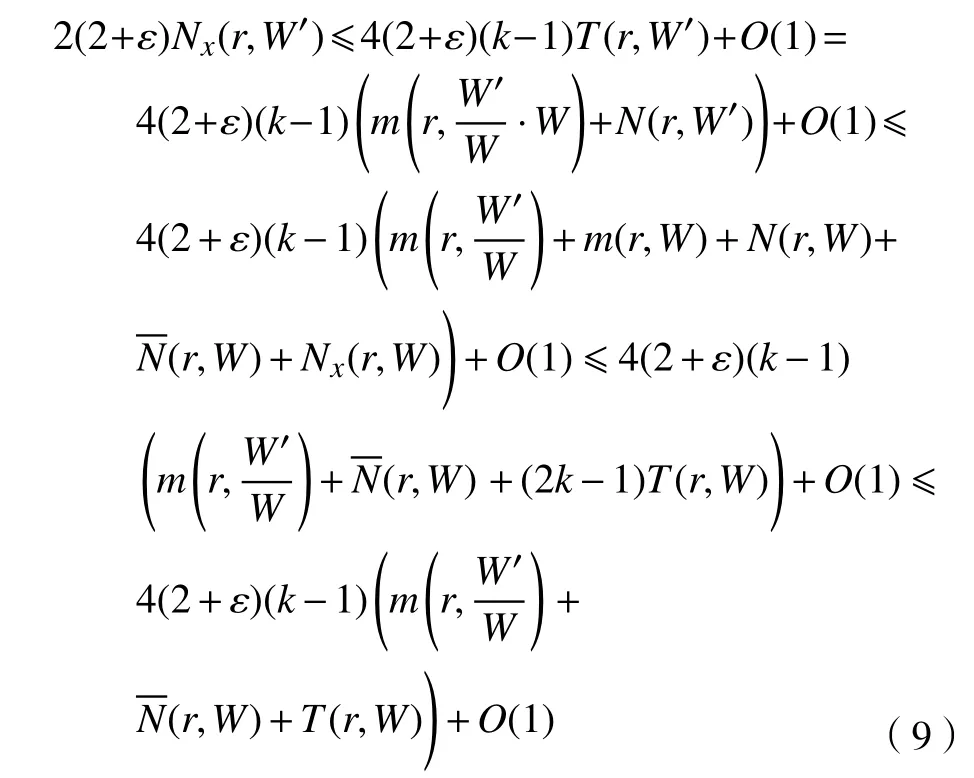
将式(9)应用于式(8),得
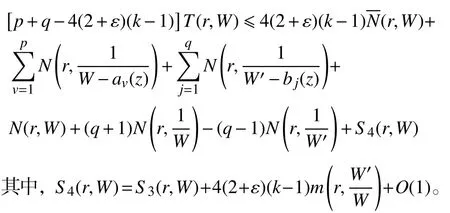
再对S4(r,W)中各项应用对数导数引理,即得定理4,证毕。
推论的证明。
结合引理1 和引理2 可得

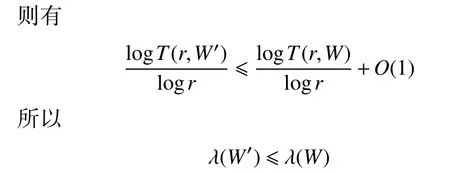
若两种情况同时成立,则结合定理4 可得

矛盾,得证。
