带参数的渐近线性椭圆方程组解的分歧性
2020-04-10马洋洋
马洋洋,贾 高
(上海理工大学 理学院,上海 200093)
1 问题的提出
考虑带参数的渐近线性椭圆方程组
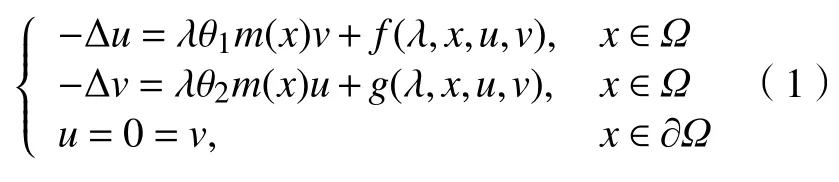
在共振和共振附近正、负解的存在性与分歧性,其中,Ω ⊂RN(N≥2)是带有光滑边界的有界区域,λ∈R是参数,θ1,θ2(θ1≠θ2)是2 个正常数,m(x)>0 a.e.x∈Ω是一个L∞(Ω)函数,非线性项f,g:R×Ω×R×R→R满足下面条件:
(h1)f和g是 Carathéodory 函数;
(h2)存在2 个非负函数b1(x),b2(x)∈Lr(Ω)(r>N)和2 个常数k,l>0,使得
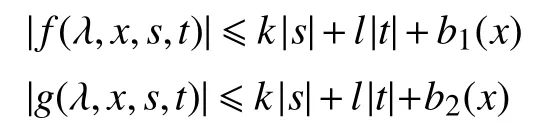
其中,|s|表示实数s的绝对值;
(h3)当 λ在某闭区间上以及a.e.x∈Ω,有

一致成立。
在20 世纪70 年代初,Rabinowitz[1-2]建立了关于算子方程的大范围分歧理论,后来Dancer[3-4]又建立了单边分歧理论,上述理论是有关方程分歧性研究所得到的相对成熟的结果。基于上述2 个理论,文献[5]给出了偏微分方程形如-Δpu+λm(x)|u|p-2u=φ(λ,x,u)(p≥2),关于解在分歧点附近产生分歧的充分条件。Chhetri 等[6-8]将文献[5]中的问题推广到方程组,其中,文献[8]所研究问题的非线性项关于变量u,v是一致有界的。本文所研究的问题与文献[5-8]不同之处在于所处理问题的非线性项关于u,v具有非一致性。因此,本文的问题更具有一般性。
2 相关定义、假设与引理
基于问题(1)的特征,本文的工作空间为
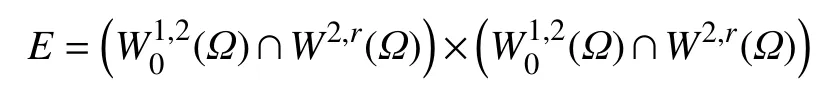
对其赋予的范数为 ‖(u,v)‖=‖u‖W2,r(Ω)+‖v‖W2,r(Ω)。
为了简化陈述,可将问题(1)改写为
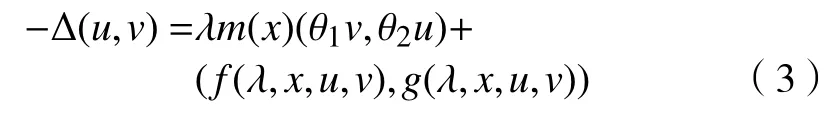
其对应的抽象算子方程为
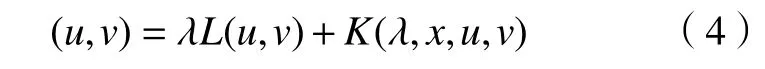
其中,L:E→E表示映射

K:R×Ω×E→E表示映射
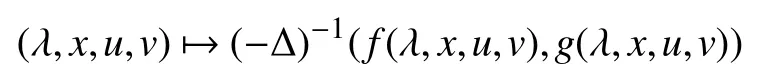
由Lax-Milgram 定理[9]可知,逆算子(-Δ)-1:(Ω)∩W2,r(Ω)是有意义的,而且还是线性、连续的。已知f,g是Carathéodory 函数,如果其对应Nemyski 算子[10]仍用f和g表示,由条件(h2)可以得到Nemyski 算子f(x,u,v)和g(x,u,v)从Lr(Ω)×Lr(Ω)到Lr(Ω)×Lr(Ω)是连续的[11]。因此,由W2,r(Ω)到Lr(Ω)嵌入的紧性可以得到K(λ,x,u,v)是全连续的。进一步,由条件(h3)可以得到,当 λ在某闭区间上,有

定义1若(λ,(u,v))∈R×E在几乎处处意义下满足问题(1),那么,本文就说(λ,(u,v))是问题(1)的强解;如果u>0且v>0或u<0且v<0,本文就说(λ,(u,v))是问题(1)的正解或负解。
定义2如果解集S={(λ,(u,v))∈R×E:(λ,(u,v))满足(1)}中存在序列{(λn,(un,vn))}满足λn→λ∞,‖(un,vn)‖E→+∞(n→∞),那么,本文就说 λ∞是问题(1)的一个无穷分歧点。
引理1[7]设0 <μ1≤μ2≤μ3≤···≤μn≤···是边值问题
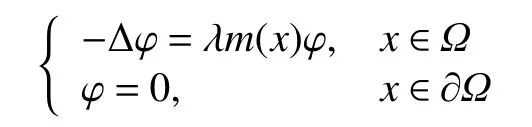
的特征值序列,并且φk∈(Ω)表示特征值 μk所对应的特征函数,那么,对于边值问题
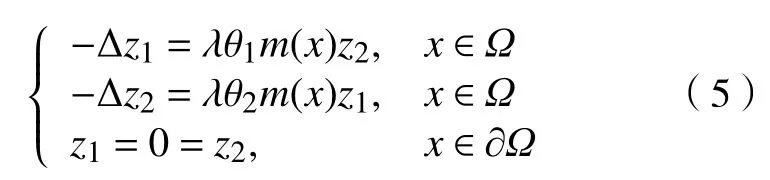
有以下结论:
引理2[1]如果条件(h1)—(h3)成立,那么,解集S存在着1 个无界部分Dτ1,并且Dτ1能够分解成2 个子连续统。进一步,在空间R×E中存在着(τ1,∞)的邻域O,使得当(λ,(u,v))∈)∩O且(λ,‖(u,v)‖E)≠(τ1,∞)时,有(λ,(u,v))=λ,α(,+v⊥)),其中,,当α >0(α <0)且|α|→+∞时,有|λ-τ1|→0且
现定义一些记号。设h(λ,x,u,v)=f(λ,x,u,v)+g(λ,x,u,v),对于 γ≥0,R+=[0,+∞),定义:Ω×(0,+∞)×→R和,:Ω×(-∞,0)×以及(x)和(x)如下:
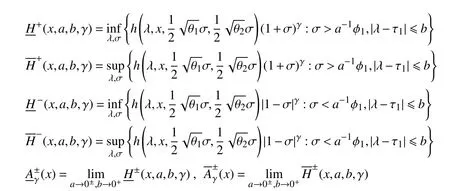
假设1存在0 ≤γi<2-以及非负函数Bi(x)∈Lr(Ω),对于i=1,2,3,4,使得
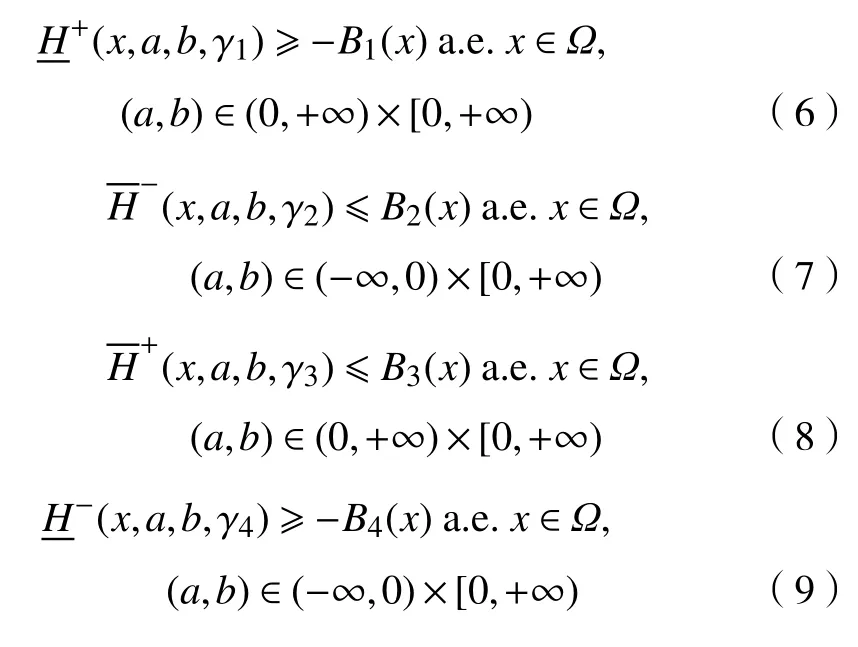
3 主要结果及其证明
定理1如果(h1)—(h3)成立,则存在ε >0满足τ±k∉[τ1-ε,τ1+ε](k≠1),使得当任意的(λ,(u,v))∈S∩Oε时,有u>0且v>0或u<0且v<0。此外,存在由正解和负解所组成的连续统和⊂S在 τ1处无穷分歧,其中,

证明第一部分的证明。可将空间E分解为
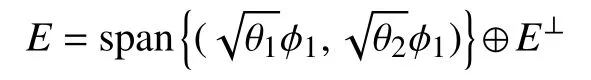
其中

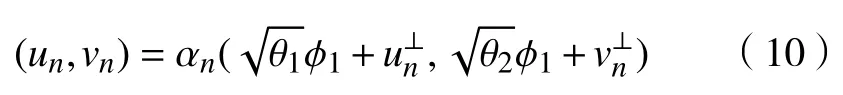
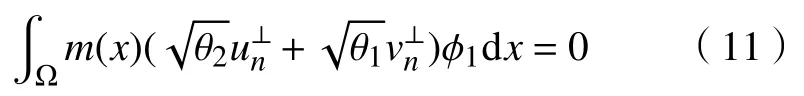
根据文献[7]中的引理4.2 可得,当n→+∞时,|αn|→+∞当且仅当‖(un,vn)‖E→+∞。事实上,由式(10)和式(11)可以得到
其中,“+”和“-”分别表示 αn的符号,并且当n→∞时,αn→∞。
第二部分的证明。因为,τ1是代数单重的,由引理2 可得,存在2 个连续统⊂S和⊂S。由定理1 的第一部分可知,当(λ,(u,v))∈S∩Oε时,有u>0且v>0或u<0且v<0,于是,取∩Oε,⊂S分别由正解和负解组成。再由引理2 以及分歧的定义可知,和在τ1处无穷分歧。定理1 证毕。
定理2假设(h1)—(h3)成立。


定理3假设(h1)—(h3)成立。

证明由于定理2 和定理3 的证明类似,所以,现只给出定理2 的证明。

上式化简为
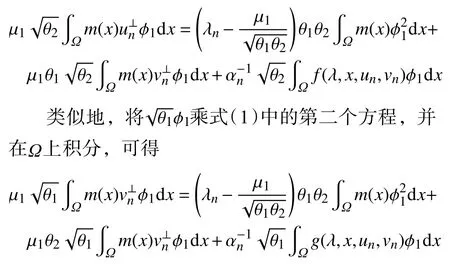
将上面2 个式子相加,有

现在分两步来说明式(17)是不正确的。
第一步证明存在,使得下面不等式成立:


第二步说明式(17)是不成立的。
由式(21)并结合Fatou 引理可得

现在需要验证不等式(i),(ii),(iii)。不等式(i)可由Fatou 引理得到,不等式(iii)是本文的假设条件,接下来,说明不等式(ii)成立。设n固定,则由式(20)可得

从而看出(i),(ii),(iii)是成立的,进而得到式(17)与式(23)是矛盾的。于是,定理2 中a 的(a)是成立的。
在定理2 中,关于结论b 的证明,类似地,即对αn<0以及充分大的n,有

从而可以得到与式(18)~(22)类似的结论。再根据假设式(7),运用Fatou 引理得到与式(21)类似的不等式,进而得到矛盾。这样就完成了定理2 的证明。
