基于渠道竞争与品牌竞争的供应链定价策略和协调研究

霍良安，蒋杰辉，王绍凡，陈彬彬

（上海理工大学 管理学院 上海 200093）

在传统的零售渠道中，制造商大部分通过强势的大型零售集团进行销售，大型零售集团在整条供应链的博弈中往往享有更大的权力。随着网络经济的兴起，越来越多的制造商可以通过直销模式来重塑自身的零售渠道，进而在供应链中获得更大的利润，如联想公司、苹果公司和戴尔公司等,开通了网上直销渠道,形成了网上直销渠道和传统零售渠道并存的双渠道供应链，双渠道供应链中渠道定价和协调策略研究也因此倍受关注。

已有一些学者对渠道竞争环境下制造商与零售商之间的渠道价格冲突及相应的定价策略问题进行了研究。文献[1]构建了传统零售商销售和制造商直接销售之间的竞争模型，研究了信息扩散对供应链系统的影响。Yao 等[2]分析了传统零售渠道和网上销售渠道之间的消费者购买选择意向，在一定条件下，客户需求在这两种渠道上是稳定的。Chiang 等[3]研究了传统制造商和渠道合作伙伴之间的价格竞争关系，制造商直接增加直售渠道能够减少利润损失的风险。文献[4-6]进一步证实了类似的结论。Huang 等[7]研究了制造商同时开辟直销渠道和零售渠道与制造商只有网络直销渠道两种模式对比的最优定价策略。熊中楷等[8]研究了由一个制造商和一个网络直销的零售商组成的供应链定价策略和协调机制。以上研究大多只关注于传统零售渠道和网络直销渠道销售模式下单一产品的价格竞争，而没有考虑两种渠道销售模式下制造不同品牌之间竞争的问题。

Yao 等[9]构建了零售渠道和网上分销渠道的价格竞争模型，比较了Stackelberg 和Bertrand 两种决策下价格的竞争关系。Dumrongsiri 等[10]研究了关于零售和直接销售双渠道的供应链，具有一个双渠道的供应链系统对制造商来说很有利。Huang等[7]分析了通过互联网销售产品和传统销售产品的零售商的最优定价策略。Avery 等[11]研究发现，在零售渠道基础上添加一个互联网渠道，有利于增加渠道利润。Niu 等[12]研究了垄断环境下的两级零售商供应链模型中联合定价和分散决策，在一个渠道的定价和决策会影响其他渠道的定价和决策。Li 等[13]研究了基于分散式和集中式决策模式的两级双渠道供应链的定价策略，在不同的市场份额条件下，零售商应该选择不同的直销模式以获取最大利润。Kurata 等[14]研究了制造商品牌和零售商自主品牌产品在两种渠道销售模式下的价格竞争，探讨了跨品牌、跨渠道的定价政策，并对供应链协调进行评估。曹宗宏等[15]研究了开通直销渠道和提供自有产品的条件、双方的定价策略和供应链的均衡结构问题，当直销渠道的操作成本和自有产品的单位成本较低时，双方的竞争可以降低因双方独立决策而引起的双边际效应的负面影响，实现双赢。杨帆等[16]研究了供应链中渠道竞争与品牌竞争共存时，制造商与零售商的定价博弈问题，制造商与零售商可以通过增加消费者对自身品牌的忠诚度来增加利润，而制造商不能通过建立制造商品牌的渠道忠诚度来增加利润；Stackelberg 定价博弈的主导者有获得更大利润的优势。通过对以往文献的回顾，可以看出目前的研究或仅考虑渠道竞争时的产品定价或仅考虑品牌竞争时的产品定价，而对渠道竞争与品牌竞争共存的供应链中产品定价问题的研究不多见。

大量学者研究了关于供应链渠道的选择和权利结构的不同方面的影响[17-20]。许传永等[21]研究发现直销渠道会降低产品的价格并且增加产品销量。Yoo 等[22]研究表明线上网络渠道并不一定会使零售价格降低，以及网络渠道在渠道结构和市场环境中影响不同。Zhang 等[23]研究了在双渠道中的不同权利结构下，产品的可替代性和渠道结构对价格决策的影响。Lu 等[24]从供应商的角度研究了实体零售商和电子商务组成的混合双渠道供应链系统的定价策略。与已有研究文献不同，本文基于制造商的视角，主要研究了两个制造商同时拥有线上和线下销售渠道组成的竞争供应链系统，研究两个制造商之间的价格博弈，分析消费者对产品或渠道的选择差异系数对销售价格和利润的影响。根据不同的权利结构，分析供应链系统中渠道竞争与品牌竞争共存时，两个制造商的Nash 博弈决策和合作博弈决策定价问题，探讨了渠道竞争对价格决策和系统利润的影响。在此基础上提出线上和线下竞争供应链的共同调价机制，从而实现了线上和线下竞争供应链的利润最大化。

1 问题描述与符号说明

本文考虑由两个竞争的制造商同时拥有线上和线下销售渠道组成的供应链系统，其组织结构和产品销售渠道如图1 所示。

制造商i(i=1,2)生产性质和功能相同的同款产品，其单位制造成本和单位销售成本分别为ci m和cij。在渠道j（j=1,2;1 表示线上销售渠道，2 表示线下销售渠道）以单位价格Pij(Pi j＞ci m+cij)通过线上和线下渠道销售产品。

图1 O2O 竞争供应链系统Fig.1 Competition system of the O2O supply chain

假设各渠道产品的市场需求均是随机的，第i个制造商的第j种销售渠道产品需求为

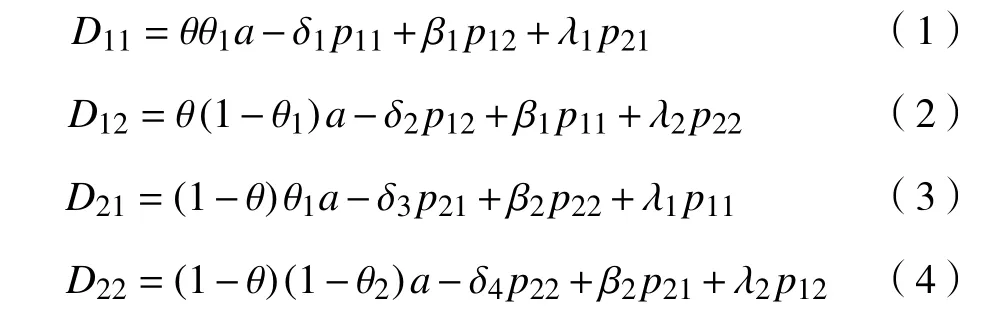
式中：a为 产品的市场需求总量；θ表示制造商M1占有的市场比例，θi(i=1,2)表示制造商Mi的线上销售渠道占制造商Mi市场需求总量的比例，βi(i=1,2)表示消费者对制造商Mi线上和线下渠道的选择差异，βi越大，表示渠道的差异越小（两种渠道的竞争或替代性越小）；λj(j=1,2)表示消费者对制造商M1和制造商M2在同一渠道j的产品选择差异，λj越大，表示产品在渠道j的差异越小（两种产品在同一渠道的竞争或替代性越小）；δk(k=1,2)表示消费者对制造商M1的单位销售价格p1k的敏感系数，δk(k=3,4)表示消费者对制造商M2的单位销售价格p2,k-2的敏感系数，满足θ,θ1,θ2∈(0,1);0 ＜βi,λj＜δn(n=1,2,3,4)；pij分别表示第i个制造商在第j销售渠道的产品销售价格。

根据上述构建的供应链系统和需求函数，可得制造商Mi(i=1,2)的利润函数ΠMi和供应链系统总利润ΠMi1如下：

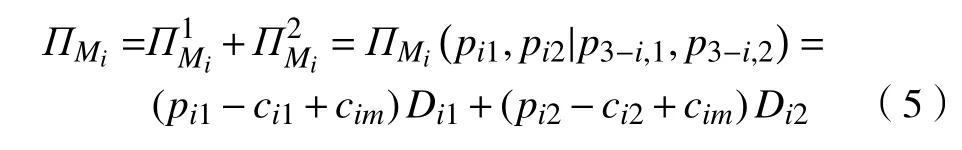
式中，第一部分为制造商Mi在线上销售渠道的利润函数，第二部分为制造商Mi在线上销售渠道的利润函数

线上和线下竞争供应链系统总利润 Π1为

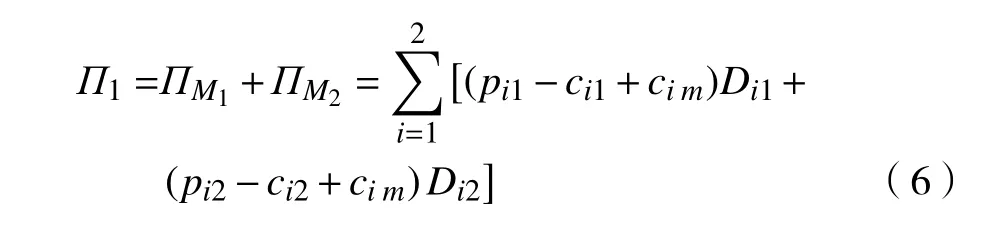
2 线上和线下竞争供应链的决策模型

2.1 Nash 博弈决策模型

在Nash 博弈决策系统中，假设实力相当的两个制造商M1和制造商M2同时决策定价策略使其自身利润最大化。决策的过程如下：在给定制造商M2的定价策略下，制造商M1决策产品在线上渠道的单位销售价格p11和线下渠道的单位销售价格p12；同时在给定制造商M1的定价策略下，制造商M2决策产品在线上渠道的单位销售价格p21和线下渠道的单位销售价格p22。Nash 博弈定价策略确定的最大目标利润函数为

目标利润函数具有性质1。

性质1ΠMi是关于线上渠道销售价格pi1和线下渠道销售价格pi2的严格凹函数。

证明将式（5）分别对线上销售价格pi1和线下渠道销售价格pi2求一阶导数，可得：

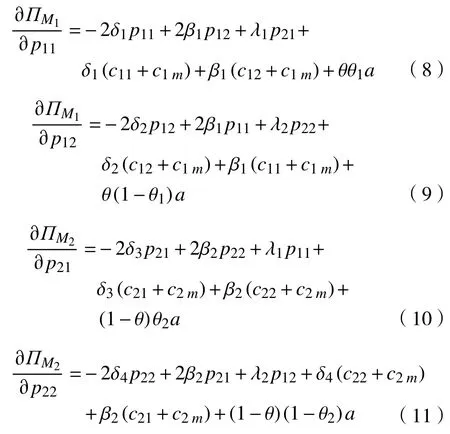
同理，可得制造商Mi的利润函数ΠMi关于线上渠道销售价格pi1和线下渠道销售价格pi2的Hessian矩阵H1和H2分别为

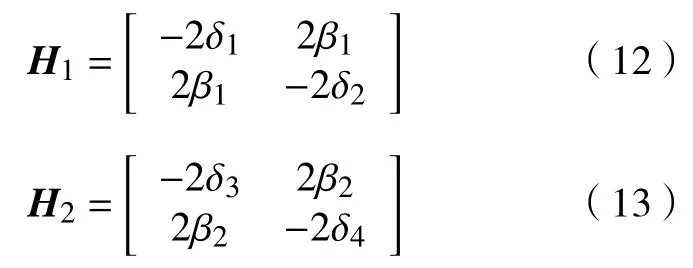
性质1 表明ΠMi是关于线上渠道销售价格pi1和线下渠道销售价格pi2的严格凹函数，制造商Mi的目标函数存在唯一的最大值。

定理1Nash均衡价格。当时，制造商Mi最优化的线上渠道销售价格pi1和线下渠道销售价格pi2满足：

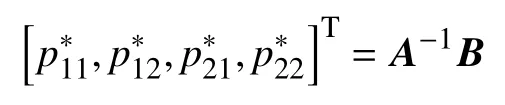
其中，

证明令式（8）～（11）右边等于零，并写成矩阵形式，可得

由需求函数式（1）～（4）和利润函数式（5）易得，B＞0，当＞0时，方程组AP*=B存在唯一的正解，即P*=A-1B。

定理2价格敏感性分析。制造商Mi最优化的线上渠道销售价格pi1和线下渠道销售价格pi2对渠道的选择差异参数 βi、产品的选择差异参数 λj和消费者对价格的敏感性参数 δk分别有：

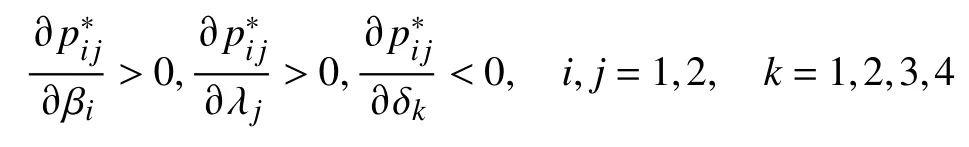
证明运用静态分析的方法，由定理1可知，当＞0时，方程组AP*=B存在唯一的正解。将方程组（12）分别对 δ1求导化简可得

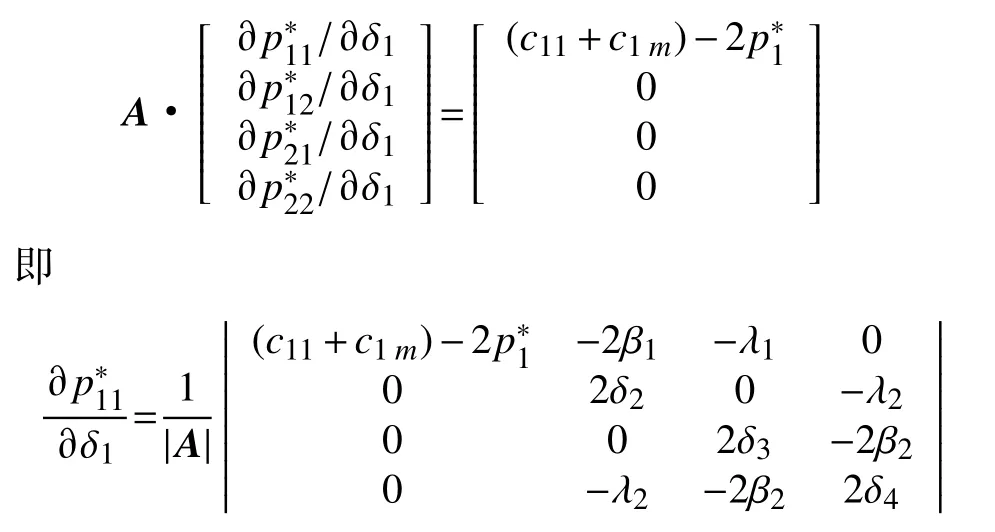
由|A|＞0可知，行列式

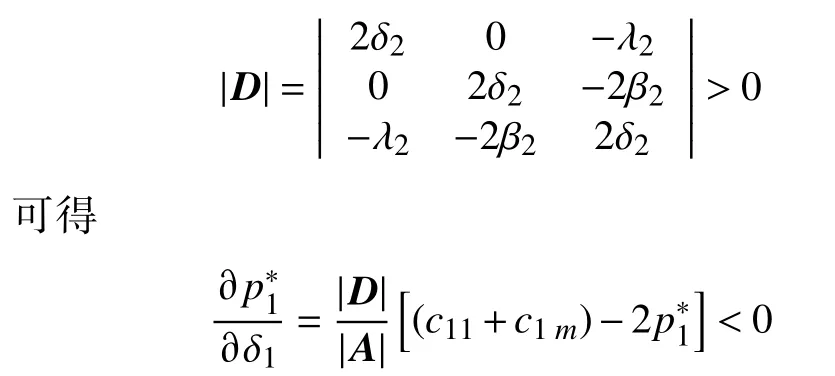
定理1 和定理2 表明，当价格系数矩阵A正定时，供应链系统的Nash 博弈决策存在最优定价策略。固定其他参数不变时，制造商Mi线上和线下渠道竞争或者制造商之间的产品竞争越激烈（βi或 λj越小），最优渠道销售价格pij越低。

定理3制造商最优利润的影响分析。

假设制造商Mi(i=1,2)在线上销售渠道的利润函数为，线下销售渠道的利润函数为。则有：

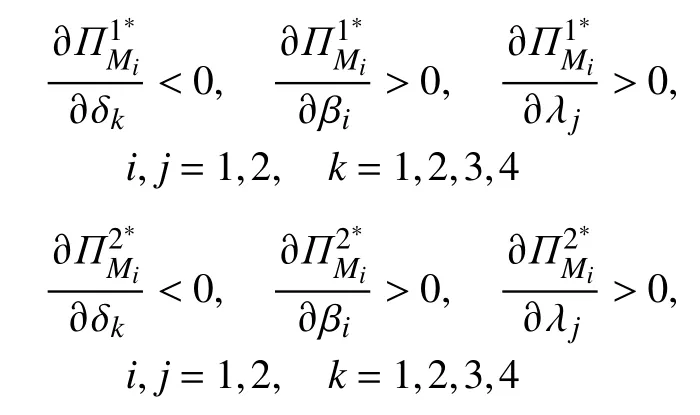
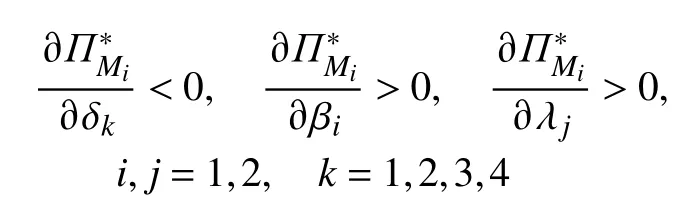
证明运用包络定理（Varian,1992）对制造商的最优利润函数对参数 δ1求偏导数，可得

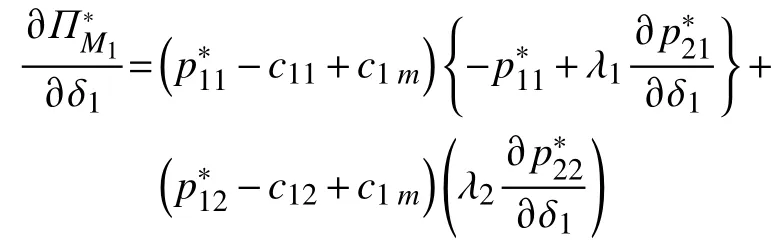
定理3 表明，当价格系数矩阵A正定，固定其他参数不变时，制造商Mi线上和线下渠道竞争或者制造商之间的产品竞争越激烈（βi或 λj越小），最优渠道销售利润越低。

2.2 合作博弈决策模型

在由两个制造商组成的供应链系统中，两个制造商通过合作采用合作博弈以实现整体利润最大化。整个供应链系统的最优化目标利润函数为

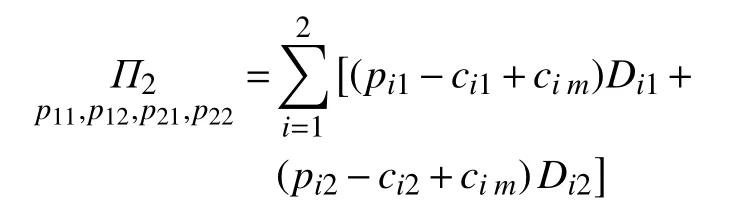
性质2合作博弈决策下总利润函数的凹性。Π2是关于销售价格p11，p12，p21和p22的凹函数。

证明同性质1，目标利润函数关于销售价格pij的Hessian 矩阵为

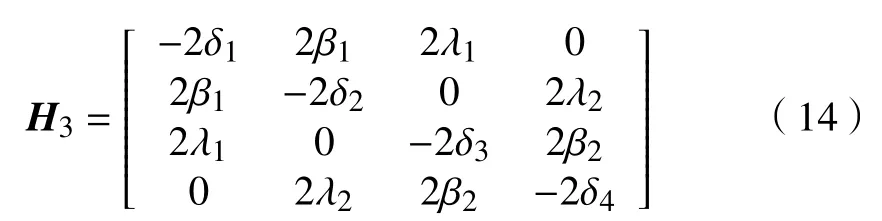
定理4合作博弈决策下的最优定价策略。在合作博弈决策中，最优定价策略分别为

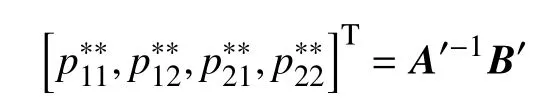
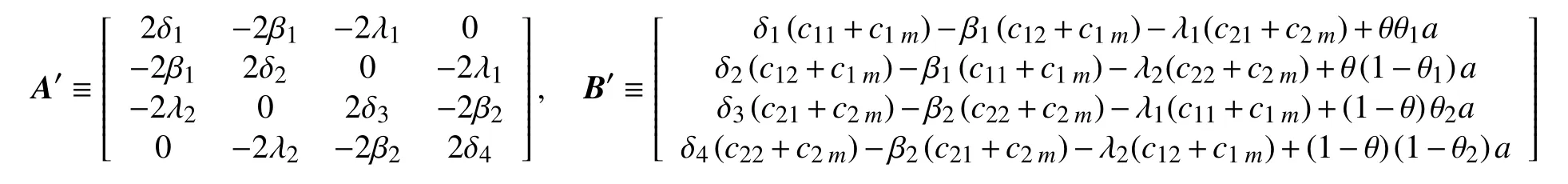
证明同定理1。

3 线上和线下竞争供应链的协调策略

在供应链的研究领域中，供应链的协调机制使供应链系统的利润更进一步优化，使协调后的系统利润能够最大程度地接近合作博弈决策时的整体最优利润，进而优化Nash 博弈决策时的供应链系统利润。

Nash 博弈决策下，整个供应链系统的最优利润为

合作博弈决策下，整个供应链系统的最优利润为

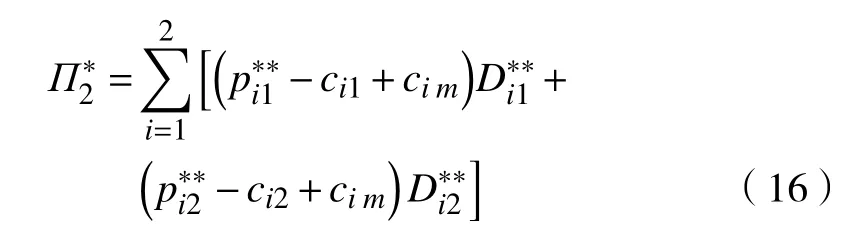
定理 5对Nash 博弈模型与合作博弈模型比较分析，可得：

证明a.由最优化理论可知，定理5 的a 明显成立。

c.由于供应链系统总目标利润函数是价格pij的凹函数，当价格pij偏离最优价格策略时，利润也将急剧减少。

定理5 表明，当Nash 博弈模型的最优价格与合作博弈模型的最优价格差异越大，两种决策之间的利润差额也越大。

由于制造商之间通过竞争的方式扩大市场份额，通常会采用降价的方式吸引消费者购买其产品。竞争越激烈，渠道的利润越低，基于以上思想，本文通过供应商合作的方式，采取联合调价的策略来协调线上和线下竞争供应链，使供应链系统中制造商双方的利润同时提升。

定理6供应链协调。存在，i,j=1,2。通过联合调价的方式能够实现Nash 博弈决策下的供应链最大化，使得。

证明令,i,j=1,2。代入Nash 博弈决策的供应链系统总利润函数，可得

定理5 和定理6 表明，Nash 博弈决策存在利润损失。即Nash 博弈决策的利润和价格一般都是低于合作博弈决策下的利润和价格。两个制造商之间通过合作博弈模型，通过调价的方式可以实现线上和线下供应链的协调，使整体的利润最优化。

4 算例分析

为了更清楚地阐述上面的结论，这里对上述结论作进一步的数值仿真。根据前面模型的基本假设条件，取cm1=40,cm2=30,c11=3,c12=5,c21=4,c22=6,δ1=2,δ2=2.5,δ3=2.5,δ4=3,β1=0.2,β2=0.1,λ1=0.4,λ2=0.2,θ=θ1=θ2=0.5,a=1 000。满足性质2 存在的条件：用Matlab 软件将符合条件的参数值代入式（15）和式（16），求得Nash 博弈决策与合作博弈决策下各决策变量的最优解和协调策略，如表1 所示。

4.1 选择差异系数的敏感性分析

a.消费者对制造商Mi的渠道选择差异系数βi(i=1,2)对价格和利润的影响。

βi(i=1,2)之间有相似的结论，本文以 β1为例，分析其变化对价格和利润的影响。由图2 和图3可知，随着制造商M1线上和线下渠道的选择差异系数 β1的变小（竞争的变大），渠道的销售价格pij和利润都随之减少。

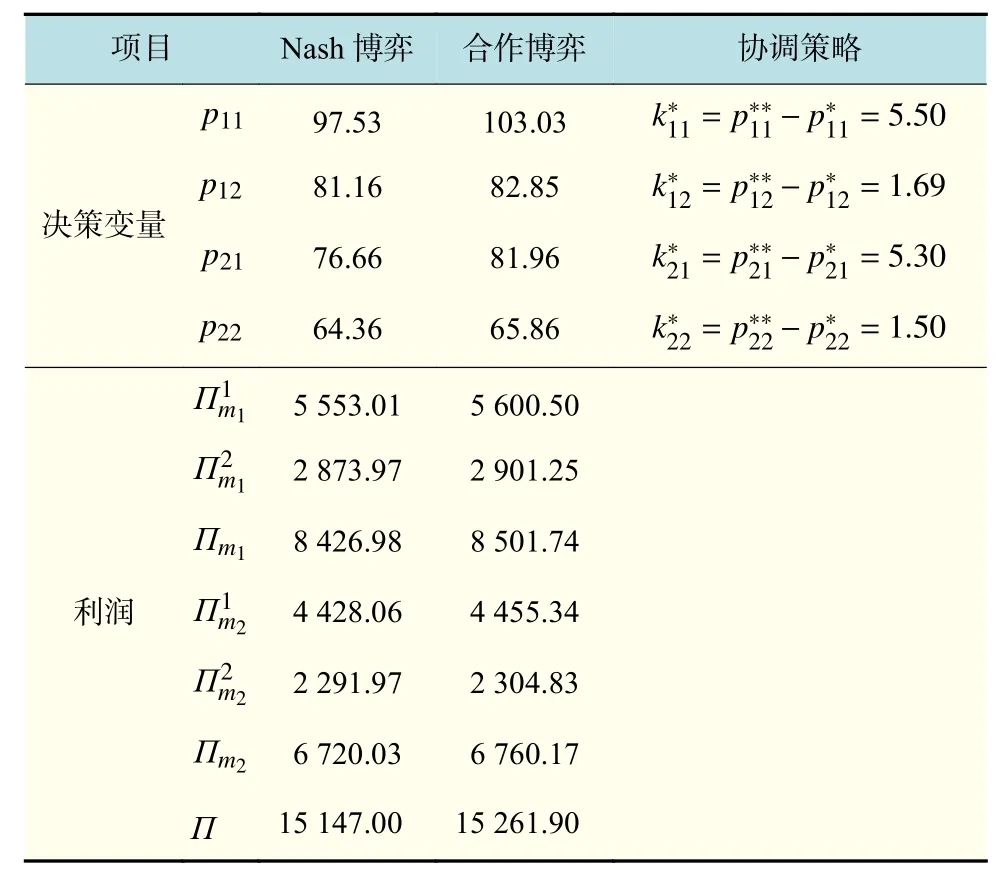
表1 线上和线下竞争供应链系统各决策变量的最优解和协调策略Tab.1 Optimal solution and coordination strategy of each decision variable in the competition system of the O2O supply chain

由图2 可知，制造商M1的渠道销售价格p1j随消费者的渠道选择差异系数 β1变化程度比制造商M2的渠道销售价格p2j随消费者的渠道选择差异系数 β1变化程度大。因为，β1是直接影响制造商M1的销售价格p1j；而 β1是间接影响制造商M2的需求量，进而影响制造商M2的销售价格p1j。由图3 可知，消费者对制造商Mi的渠道选择差异系数βi(i=1,2)对利润的影响与其对价格的影响相似。

从仿真模拟结果也可以看出，供应链系统的Nash 博弈决策存在最优定价策略。固定其他参数不变时，制造商Mi线上和线下渠道竞争或者制造商之间的产品竞争越激烈，最优渠道销售价格pij越低。

b.消费者对制造商Mi之间的产品选择差异系数λj(j=1,2)对价格和利润的影响。

由图2 可知，固定其他参数不变，当λ1=0.4，λ2的值由0.4 变为0.2 时，制造商的销售价格pij随之减少（由图中细实线变为虚线）。但是，λ2的变化对线上销售价格p1j影响小于其对线下销售价格p2j影响。固定其他参数不变，当λ2=0.4，λ1的值由0.4 变为0.2 时，制造商的销售价格pij随之减少（由图中细实线变为粗实线）。但是，λ2的变化对线下销售价格p2j影响小于其对线上销售价格p1j影响。同理，分析图3，可验证定理3。固定其他参数不变时，制造商Mi线上和线下渠道竞争或者制造商之间的差异系数越小，最优渠道销售利润越低。

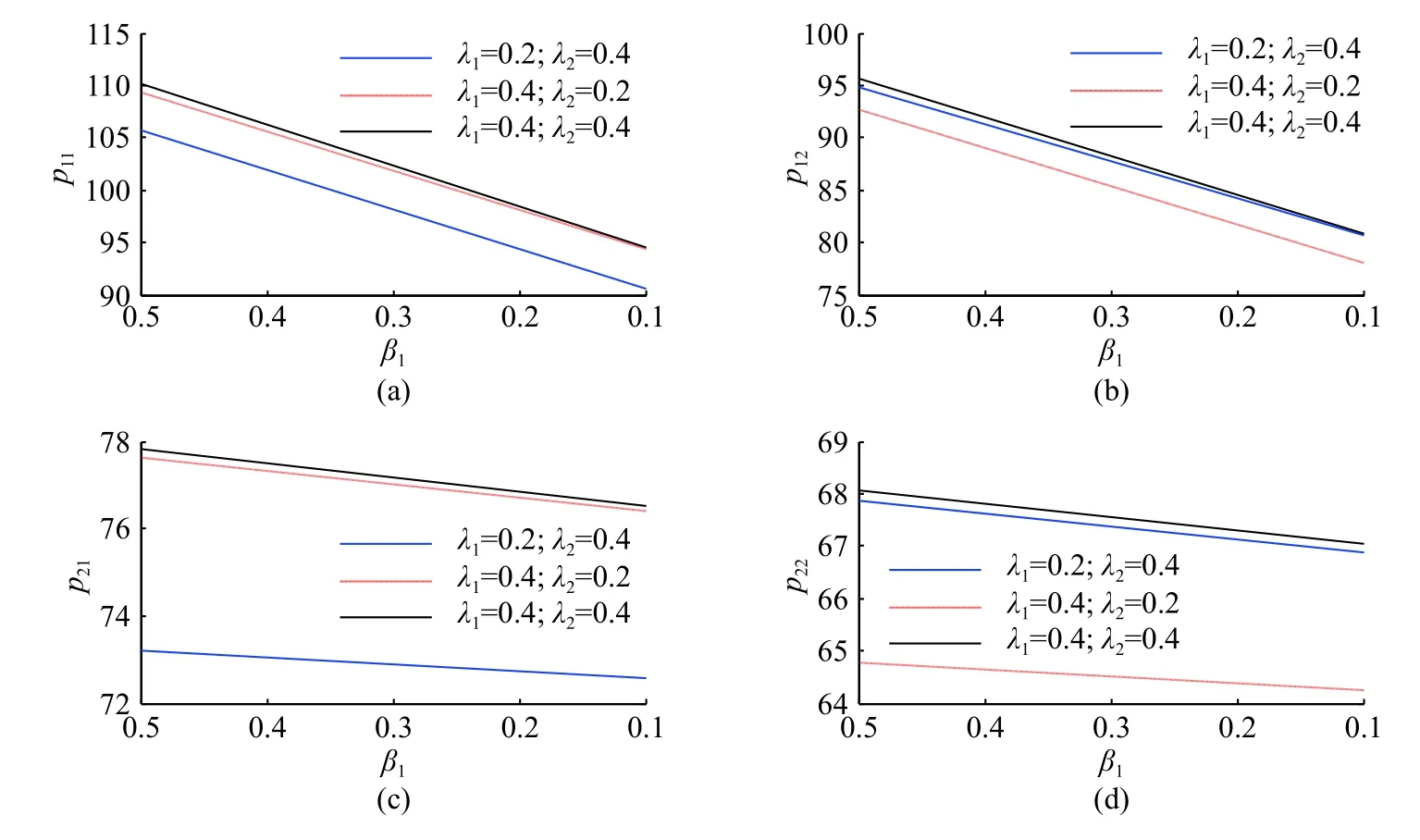
图2 Nash 博弈决策下的渠道的差异系数 β1对销售价格pij 的影响Fig.2 Impact of the channels difference coefficient β1on the sale pricepij based on the Nash game model

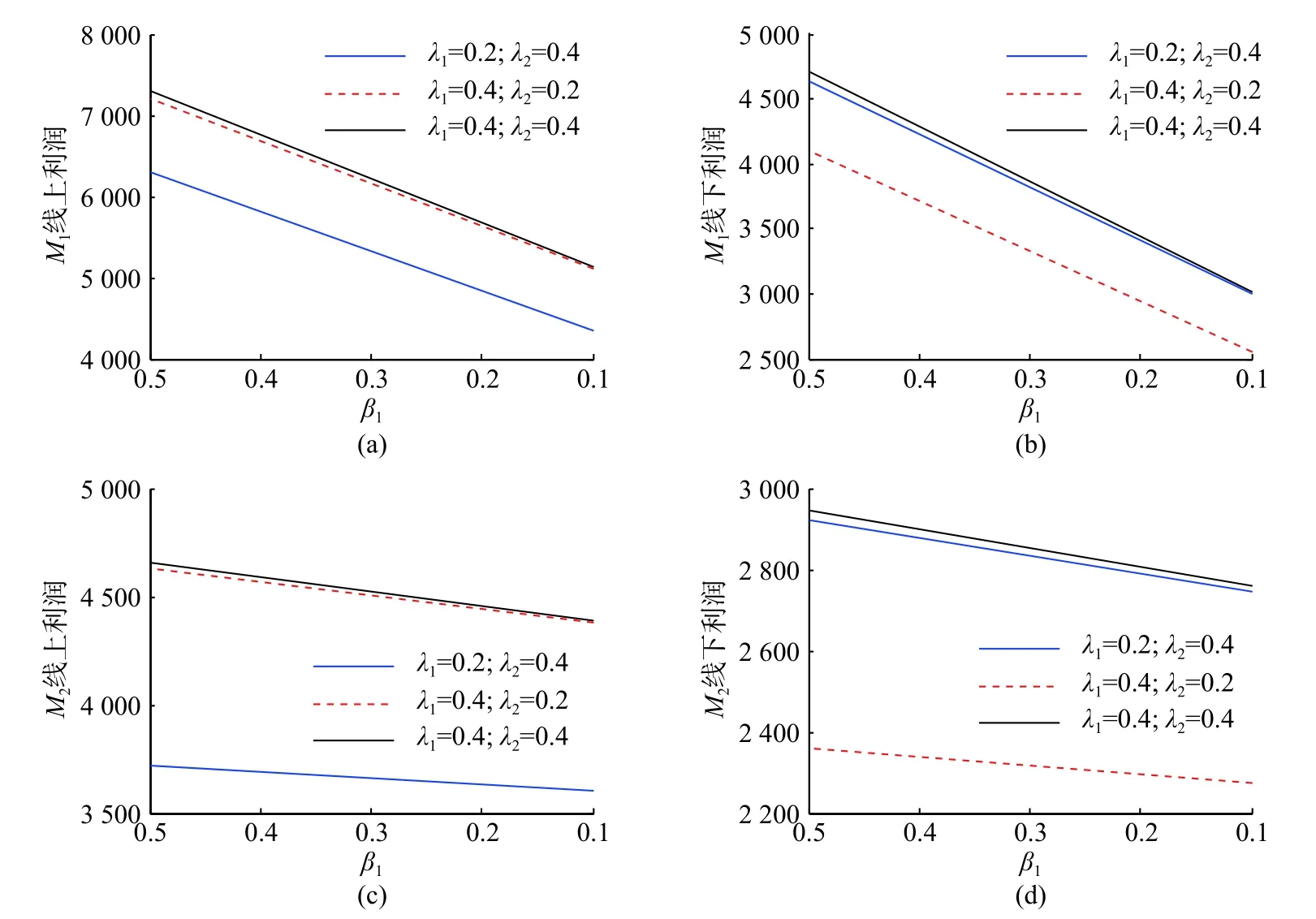
图3 Nash 博弈决策下的渠道的差异系数 β1对利润 的影响Fig.3 Impact of the channels difference coefficient β1on the profit based on the Nash game model

4.2 线上和线下竞争供应链的协调策略

由于制造商之间通过竞争的方式扩大市场份额，通常会采用降价的方式吸引消费者购买其产品，竞争越激烈，渠道的利润越低。由表1 可知，合作博弈决策时制造商Mi渠道销售价格pij和渠道利润均高于Nash 博弈决策时的渠道销售价格pij和渠道利润。通过制造商之间合作以共同调价的方式能提高Nash 博弈决策下各渠道的利润，协调后的线上和线下竞争供应链系统利润与合作博弈决策时相等，即实现了供应链系统的最优化。

5 结束语

建立了由两个竞争的制造商同时拥有线上和线下销售渠道组成的供应链系统，假设各渠道的需求量为线性的条件下，探讨了两个制造商之间的价格博弈问题。对线上和线下竞争供应链在Nash 博弈决策和合作博弈决策模式下，研究了两个直售的制造商之间的价格博弈。分析了消费者对产品或渠道的选择差异系数销售价格和利润的影响，在此基础上，提出了线上和线下竞争供应链的共同调价机制，从而实现了线上和线下竞争供应链的利润最大化。本文仅研究了制造商直接销售产品且在确定需求下的线上和线下竞争供应链，未来可进一步探讨随机需求、零售商加入供应链系统、政府补贴、广告策略等方面的问题。