广义变系数BKP方程的lump解

杨 梅

(重庆电子工程职业学院，重庆 401331)

非线性演化方程对于描述非线性物理现象非常重要。研究这些非线性演化方程的解析解变得越来越重要。为了研究非线性方程，研究者们提出了许多方法，例如逆散射变换[1]，Darboux和Bäcklund变换[2]和Hirota双线性方法[3]。这些方法中的每一种都有其特点，但是Hirota双线性方法更具启发性，可以直接为大量非线性演化方程提供多孤子解。此外，将Hirota直接法与Riemann theta函数相结合是一种解决非线性演化方程精确的显式周期波解的可行方法[4]。

本文调查如下(3+1)维广义变系数B-type Kadomtsev-Petviashvili(BKP)方程[4]

(1)

其中u=u(x,y,z,t),hi(t)(i=1,2,3,4,5)是任意解析函数。它描述了弱色散准介质中的波传播与流体力学。Tu等[4]基于贝尔多项式，分别推导了方程(1)多项式孤子解和双线性形式。此外，通过使用黎曼θ函数，他们还构造了方程的一周期和二周期波动解。方程(1)包含了两种重要的非线性发展方程。

(1) 当h1(t)=1,h2(t)=-5,h3(t)=15,h4(t)=45,h5(t)=0,方程(1)变成一个(2+1)维非线性BKP方程[5]。

(2)、当h1(t)=1,h2(t)=-5,h3(t)=15,h4(t)=45,h5(t)=χ,方程(1)变成一个(3+1)维非线性BKP方程[6]。

接下来，我们将利用Hirota双线性方法求方程(1)的lump解,并结合指数函数和三角函数讨论了lump解和不同类型孤子解之间的交互作用。

1 Lump解

定理1[4]作如下变换与限制

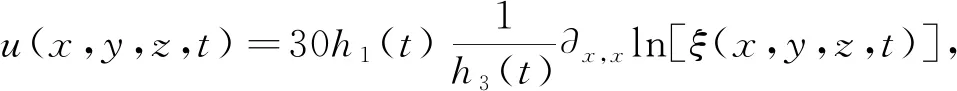
(2)

方程(1)有如下Hirota双线性形式：

(3)

方程(3)的等价形式：

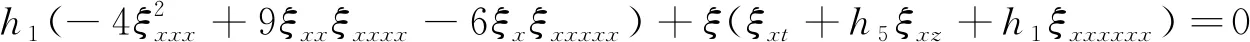
(4)

证明见文献[4]。

为了获得(3+1)维广义变系数BKP方程的lump解，我们假设方程(4)有如下形式的有理解

(5)

其中αi(i=1,2,3,6,7,8,10)都是待定常数，αi(t)(i=4,9,11)都是待定函数。将方程(5)代入方程(4),利用Mathematica软件提取x2,y2,xy等自变量的系数令之为零，可得如下解

(6)

(7)

(8)

(9)

(10)

将式(6)～式(10)代入式(2)和式(5)中，可以获得式(1)5种不同的lump解。为了观察lump解的物理结构，我们将式(6)代入式(2)和式(5)中，并令

α1=α3=-2,α2=α7=-1,α5=α8=h1=1,α6=3,α10=-10,h5=0

此时方程(1)的lump解有如下形式

(11)

当y=z=0,lump解(11)的物理结构见图1。

2 Lump解和双曲函数的交互作用

为了考察lump解和双曲函数的交互作用，我们假设

(12)

其中φi(i=1,2,3,5)都是待定常数，φi(t)(i=1,2)和φ4(t)都是待定函数。将方程(12)代入方程(4),利用Mathematica软件提取x2,y2,xy,exp等函数的系数令之为零，可得如下解

(13)

其中λ1是积分常数。

我们将(13)代入方程(2)和(5)中，可得方程(1)如下形式的交互作用解

(14)

令

α1=α3=-2,α5=1,α6=3,α10=-10,λ1=-1,φ3=-2,φ5=-3,α11(t)=2,
h1(t)=h5(t)=t,y=z=0

可得交互作用解(14)的物理结构见图2。

3 Lump解三角函数的交互作用

为了考察lump解和三角函数的交互作用，我们假设

(15)

将式(15)代入式(4),利用Mathematica软件提取x2,y2,xy,cos等函数的系数令之为零，可得如下解

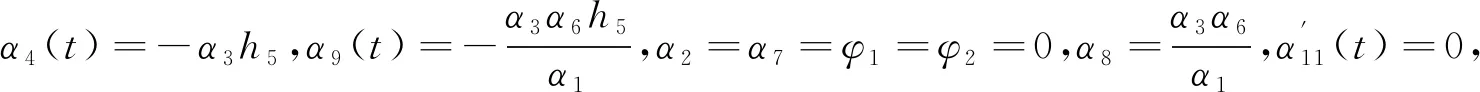
(16)

其中λ2是积分常数。

我们将(16)代入方程(2)和(5)中，可得方程(1)如下形式的交互作用解

(17)

令

α1=α3=-2,α5=1,α6=3,α10=-10,λ2=-1,φ3=-2,φ5=-3,

α11(t)=2,h1(t)=h5(t)=t,y=x=0

可得交互作用解(17)的物理结构见图3。

4 总结

(3+1)维广义变系数BKP方程方程在弱色散准介质中的波传播与流体力学等领域中起着重要应用。本文利用Hirota双线性方法和Mathematica软件[7-9]获得广义变系数BKP方程新lump解，同时讨论了lump解与指数函数和三角函数之间的交互作用，它们的物理结构通过一些三维图形和等高线图形展示在图1～图3。