基于无网格压缩感知的波达方向估计方法
2020-04-09顾旭,魏爽,李莉,苏颖
顾 旭,魏 爽,李 莉,苏 颖
(上海师范大学信息与机电工程学院,上海201418)
0 引 言
在多输入多输出(MIMO)雷达、双(多)基地和组网雷达等应用领域中,目标空域中信号密集分布的情况越来越多[1-2].由于电子干扰设备数目的急剧增加,阵列接收到的信号高度密集,如何估计空域中密集分布信号的波达方向(DOA)参数是一个研究课题.压缩感知理论的提出为提高密集信号估计的精确度提供了一种有效的求解途径[3-4].为了确保压缩感知得到精确的估计值,设计的过完备字典需要包含与真实DOA 匹配的网格[5],但是真实的DOA 值未必是整数,实现网格匹配的难度很高,通常会造成未知的DOA参数具有离格特性.
为了解决离格参数的估计问题,研究者们已提出了一系列离格类压缩感知方法.例如ZHU等[6]提出了稀疏最小二乘(STLS)方法,用泰勒展开式建立导向矢量模型;YANG 等[7]提出了离格稀疏贝叶斯(OGSBI-SVD)方法,使用奇异值分解(SVD)方法进行降维,并利用最大期望(EM)算法来迭代计算超参数;吴晓欢[8]提出了基于Cholesky 协方差分解(OGL1CCD)方法,联合稀疏性进行参数估计.但离格类压缩感知方法建立在网格划分的基础之上,造成较高的相关性以及庞大的计算量,制约了算法的性能及实际应用[9].如何从根本上解决网格划分所带来的影响,是当前用压缩感知算法解决阵列信号处理问题的一个前沿方向.
无网格类压缩感知方法无需网格划分,可以直接在连续域中进行DOA 估计.BHASKAR 等[10]提出了基于原子范数法(ANM)的线性谱估计方法;XU 等[11]提出了基于Hankel 矩阵的核范数法(nuclear norm)进行疏信号恢复;YANG 等[12]提出无网格基于稀疏迭代协方差的估计(SPICE)方法,使用功率谱密度(PSD)构建的托普利茨矩阵进行参数估计;YANG 等[13]提出基于协方差拟合准则的稀疏参数法(SPA),采用后处理方式使得参数估计唯一化,基于原子范数理论的连续压缩传感(CCS)算法[14-15],利用多个测量矢量之间的联合稀疏性进行参数估计.
本文作者针对DOA 密集分布、低信噪比的非理想情况,分别采用SPA 和CCS算法,设计了无网格的压缩感知密集DOA 估计方法,并和l1-SVD 方法[12]及离格类方法进行对比,以期提高密集DOA 的估计精度,降低计算复杂度.
1 系统模型
考虑K 个远场窄带信号源xk'k=1'2'…'K,将其入射到线性阵列,阵元接收到的目标信号的DOA 角为θk,观测模型为:



将式(1)转换为矢量模型:


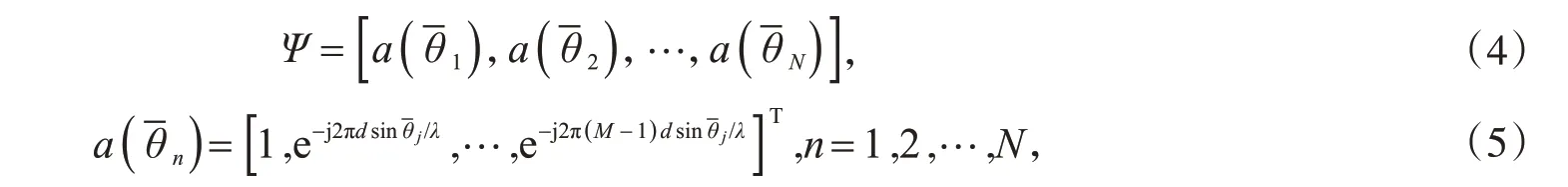

其中,Y ∈CM×K'Ψ ∈CM×N'S ∈CN×K'E ∈CM×K,这样就可以用稀疏系数矩阵S来表示观测矩阵Y.
当真实DOA 参数θk之间的间距足够小时,可以通过增大网格数N 来达到预设的网格中包含真实值的目的,但这会导致目标信号本身相关性提高,使计算量提升,而且不能准确估计出DOA 参数;另一方面,网格间距过小,或者原子范数集合的相关性过高,会引起稀疏基矩阵Ψ 内原子间的相关性提高,从而影响恢复性能.因此,采用无网格压缩感知算法求解密集DOA估计问题.
2 基于SPA的无网格压缩感知密集DOA估计方法
基于观测式(1),假设数据快拍{y(1)'y(2)'…'y(L)}是互不相关的,并且有协方差矩阵:
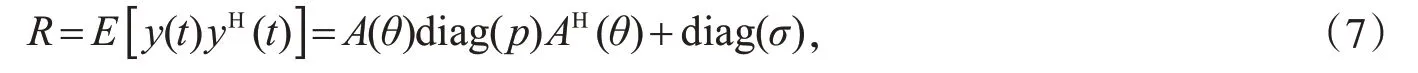
这里考虑和SPICE算法一样的协方差拟合准则:


当式(8)中f1的值最小时,样本协方差和协方差的拟合程度最高,θk最准确.根据式(7),求解f1最小化的过程是非线性的,为了便于求解(θ'p'σ),令

其中,C是一个埃尔米特-托普利茨矩阵.令C=T(u),其中,

其中,u 为托普利茨矩阵的参数.当输出阵列协方差矩阵满足托普利茨结构时,该阵列协方差矩阵可以被唯一分解.又因为DOA参数信息包含在阵列协方差矩阵中,信号的来向可以被唯一确定.
结合式(10),(11)和(7),协方差矩阵可以表示为:

根据式(12)中的协方差矩阵R,最小化式(8)中的f1:

其中,T(u)≥0表示T(u)为半正定矩阵.
在式(13)中的最小化问题可以转化为半正定规划(SDP)问题:
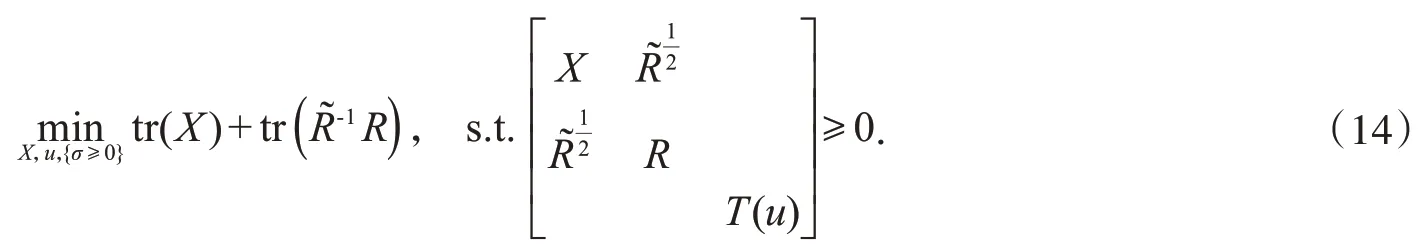
求解式(14),得到解(u*'σ*),那么R的估计值为:

通常T(u)≥0和σ ≥0,仅凭这两个条件不能从R中得到唯一的u和σ.
将式(15)转换为式(7)的形式:



当真实DOA参数θk密集分布时,直接利用协方差矩阵求解,并经过后处理使解唯一,不需要额外的稀疏基矩阵进行信号恢复,避免了因真实DOA 参数密集而导致高相关性,无法用稀疏基进行精确求解的问题.
3 基于CCS的无网格压缩感知密集DOA估计方法
最初原子范数法利用连续域的原子集合代替离散域的傅里叶频域信号,解决了频率离散化带来的网格效应,从理论上提供了信号频率精确恢复的条件[10].基于原子范数的观点,由式(3)得出信号恢复问题:

其中,Y0表示Y的无噪声情况.假设信号Y由一个原子集合中的若干个元素组成,

其中,A是CN上的一些原子构成的集合;ci为加权系数;ai为A中的原子.定义为Y的原子l0范数,
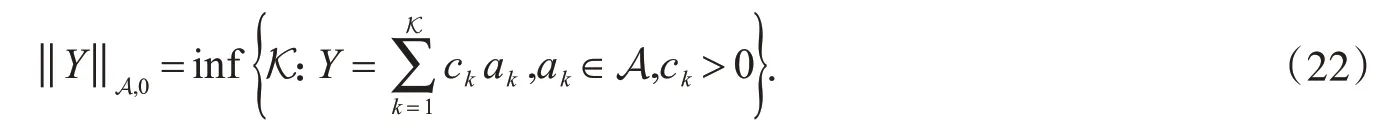
考虑到式(22)中的原子l0范数的维数是无限的,式(20)的优化问题无法计算.考虑采用由功率参数p和原子a组成的托普利茨矩阵T(u)逼近l0范数:

其中,u ∈CN;托普利茨矩阵T(u)∈CN×N;pi>0表示源功率参数.


时,可以发现T(u)在最优解时的秩Q*应该小于等于Q.
综上所述,

因此,‖ Y ‖A'0的最小化等同于式(24)的秩最小化问题:

结合式(20)可得:

在实际应用中,为了避免非凸性,同时利用稀疏性质,把式(27)转化为矩阵W 和T(u)的迹最小化问题:

利用SDP求解器进行求解,得到解u*,结合T(u*)的范德蒙分解,可以得到Y中包含的DOA参数.
4 仿 真
仿真实验中,通过比较各个方法的DOA 估计值、不同信噪比及快拍数下的均方根误差(RMSE)曲线,验证基于SPA 和CCS 的无网格压缩感知密集DOA 估计算法的优越性,同时分析对比了两种无网格的压缩感知密集DOA估计方法之间的不同.
为了让真实DOA 值尽量靠近,设两个信号的真实DOA 值分别为62.52°和63.41°,以达到空域目标密集分布效果,并且DOA 之间的间距小于网格划分类方法的网格间距,网格间距设置为1.阵列数M=20,快拍数L=200,信噪比为0 dB,信源数K=2,蒙特卡洛实验次数为50,实验结果如表1所示.

表1 各类方法的DOA估计值
从表1 中可以看出,基于SPA 的无网格压缩感知密集DOA 估计方法的估计值最准确,其次是基于CCS的无网格压缩感知密集DOA估计方法.
图1 比较了不同信噪比下各种方法的RMSE 指标.从图1 中可以看出,两种无网格的压缩感知密集DOA 估计方法,在密集DOA 以及低信噪比的非理想情况下,比其他算法的估计误差小.FOGL1CCD 是基于Cholesky协方差分解的离网重构(OGL1CCD)算法的快速算法,所以在估计精度上是一致的.基于CCS的无网格压缩感知密集DOA 估计方法的RMSE 随着信噪比的增大趋于平缓;而基于SPA 的无网格压缩感知密集DOA 估计方法的RMSE 随着信噪比的增大逐渐减小,并且其RMSE 一直低于基于CCS 的无网格压缩感知密集DOA估计方法.

图1 不同信噪比下各算法的RMSE对比图
图2 比较了不同快拍数下的RMSE 指标.从图2中可以看出,两种无网格的压缩感知密集DOA 估计方法,在密集DOA 以及低信噪比的非理想情况下,比其他算法估计误差小.在单快拍或快拍数较少的情况下,两种无网格的压缩感知密集DOA 估计方法的估计性能明显下降,随着快拍数的增大,当快拍数达到2以后,两种算法估计性能远远优于其他算法,并且基于SPA的无网格压缩感知密集DOA估计方法的性能比基于CCS的无网格压缩感知密集DOA估计方法更好.

图2 不同快拍数下个算法的RMSE对比图
5 结 论
针对DOA 密集分布、低信噪比的非理想情况,设计了一种基于SPA 的无网格压缩感知密集DOA 估计方法,以及一种基于CCS的无网格压缩感知密集DOA 估计方法.实验结果表明:这两种无网格压缩感知密集DOA 估计方法的估计效果和传统的离格类方法以及网格方法相比,密集DOA 的估计精度更高.在下一步的工作中,考虑将所设计的方法用于密集时延估计,以提高通信领域中的定位精度.
