基于加权稀疏约束的稳健Capon波束成形性能比较

林 振，李 莉，魏 爽，梁 燕

（上海师范大学信息与机电工程学院，上海201418）

0 引 言

自适应天线阵列可以根据信号环境实时地调整天线阵列的加权因子，使天线阵列的辐射方向图在期望信号方向上达到一定的增益，并抑制其他方向上的干扰，通常称这一过程为自适应波束成形（ABF）.自适应波束成形技术广泛应用于雷达、声呐、麦克风阵列语音处理、医学成像、无线通信和天文学及地震学等领域［1］.

传统的自适应波束成形算法大多假设训练数据中不包含期望信号，但是在许多实际的应用场景中，训练数据时常包含期望信号［2］.因此，当期望信号的导向矢量失配时，采用传统的自适应波束成形算法所设计的波束成形器，其性能将会急剧下降.同时，即使期望信号的导向矢量不失配，较小的训练样本也会引起波束成形器性能下降.

标准的Capon波束成形器是一种最小方差无失真响应（MVDR）自适应波束成形器［3］，其原理是保证在期望信号无失真的情况下，最小化干扰和噪声的功率.当采样数较少或是导向矢量失配时，标准的Capon波束成形器可能将真正的期望信号误认为干扰信号进行处理，稳健性较差.为了克服导向矢量失配带来的问题，出现了许多自适应波束成形器，例如：对角加载（DL）算法［4］、特征空间波束成形器（ESB）［5］、协方差矩阵锐化（CMT）方法［6］.但是，DL 算法的缺点是无法根据失配量选择最优的加载因子；ESB 算法必须首先获得子空间及其维数的先验信息，较大地限制了算法的实际应用；CMT 算法虽然能提高干扰零陷的改善程能力，但是旁瓣控制能力有一定程度的下降.程青青等［7］利用粒子群算法和其改进算法求解波束成形问题，得到的结果具有一定的稳健性，但是得到的干扰零陷和旁瓣并没有很明显的下降.

近年来，信号的稀疏表示在信号处理方面得到了许多应用［8］，ZHANG 等［9］在标准Capon 波束成形的基础上，利用信号的稀疏性，提出了基于稀疏的Capon 波束成形（SCCB）算法；在此基础上，ANDRADE等［10］提出利用l1范数解决波束成形旁瓣过高、干扰零陷不深的问题.杜永兴等［11］和刘振等［12］在标准Capon 算法的优化问题上做了改进，提出了加权稀疏约束Capon 波束成形（WSCCB）算法，得到了比较低的旁瓣和较深的干扰零陷.

本文作者主要对上述文献提出的方法进行性能的对比，定量仿真分析几种算法各自的优劣，明确未来在自适应波束成形方面的主要问题.

1 系统模型

考虑由N 个阵元组成的均匀线性阵列，阵元之间的间隔为d，存在J 个干扰信号，有J+1 个远场窄带不相关信号入射到均匀线性阵列上，如图1所示.

图1 N元线性阵列接收模型

此时，N元线性阵列接收信号的N×1维时间采样序列

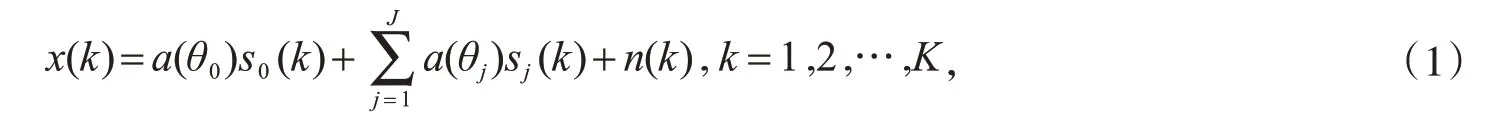
其中，k为采样时间序号；K为每条样本序列的总数；s0（k）表示k时刻的期望信号；sj（k）（j=1，2，…，J）表示k时刻第j个干扰信号.s0（k）和sj（k）的功率可以分别表示为：

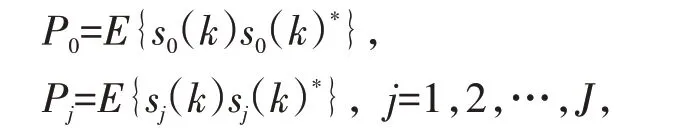
θ0表示期望信号的实际来波方向；θj（j=1，2，…，J）表示第j个干扰信号的实际来波方向；a（θ0）表示期望信号的导向矢量；a（θj）（j=1，2，…，J）表示第j个干扰信号的导向矢量；n（k）表示k时刻，方差为的加性高斯白噪声向量.信噪比可以表示为，第j个干扰信号的干噪比可以表示为根据图1可以得到：

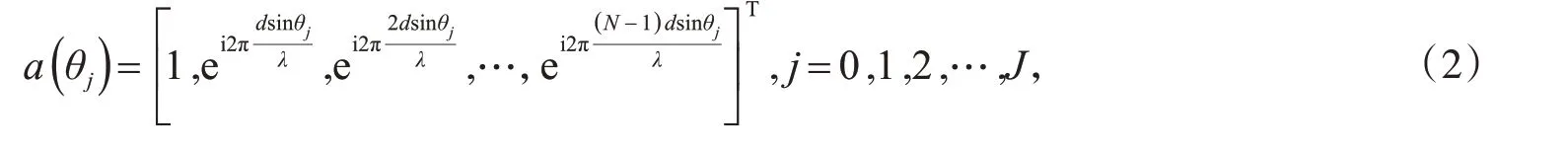
其中，d 是相邻阵元之间的间隔；λ 是窄带信号的波长，一般d=λ/2.为了更准确地得到期望信号，对阵列接收到的信号进行加权求和，k时刻的自适应波束成形器的输出记为：

其中，H为矩阵的共轭转置运算符；w=［w1，w2，…，wN］T为波束成形器对N个阵元接收信号的复加权向量，而最优的复加权向量w 能保证输出y（k）在无失真得到期望信号的前提下，将干扰信号和噪声信号的功率降到最低.

2 标准Capon波束成形

将问题转化为求解优化问题：

是干扰和噪声的协方差矩阵.但实际的采样中一般包含期望信号s0（k），很难完全分离出干扰信号和噪声信号，Ri+n可以用采样信号x（k）的协方差矩阵Rx来近似代替.将式（4）的优化问题转化为：

其中，

采用拉格朗日乘数法求解式（6），构造拉格朗日函数为：

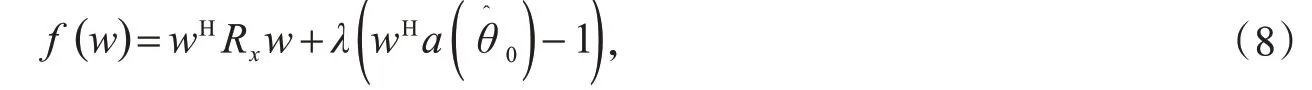
从式（9）可以看出最优权值是由Rx和共同决定的.当采样数K 较少时，天线阵列辐射方向图的旁瓣会升高，标准Capon波束成形的稳健性较差，当期望信号的DOA估计值发生偏差或者阵元位置发生偏差时，均会造成信号的导向矢量失配，进而导致标准Capon波束成形器的性能下降.

3 加权稀疏约束的Capon波束成形

针对式（9）中标准Capon 波束成形算法结果对采样数K 敏感，以及稳健性较差的问题，考虑到理想的天线阵列辐射方向图主瓣区域的天线阵列增益wHa（θ）应该近似为1，大部分旁瓣区域的天线阵列增益应该近似为0，主瓣区域远小于旁瓣区域，使得天线阵列增益在角度区域上近似满足稀疏分布，即大部分角度区域的天线阵列增益为0 或近似为0.ZHANG 等［9］将信号的稀疏性应用到Capon 波束成形器中，提出了SCCB算法，具体的优化模型如下：

杜永兴等［11］用旁瓣的阵列导向矢量的集合Aϑ的共轭转置与采样信号的协方差矩阵相乘，得到旁瓣上的信息矩阵，再取矩阵每一行的平均值（角度上信息的平均值），得到的值即为每个角度的加权值，在天线阵列辐射旁瓣所对应的干扰和噪声方向上施加了一个抑制天线阵列增益的权值.加权后的最优化模型为：

其中，γ2是稀疏项加权稀疏（γ2＞0）；Q是L×L（L为旁瓣区域内的角度总数）维的抑制旁瓣区域天线阵列增益加权矩阵；AI为干扰信号导向矢量的集合.Q是对的每一行取2范数构成的对角阵，设

其中，di是1×N的向量.令

则

刘振等［12］主要利用噪声子空间与信号子空间之间的正交性构造加权矩阵G，优化模型为：

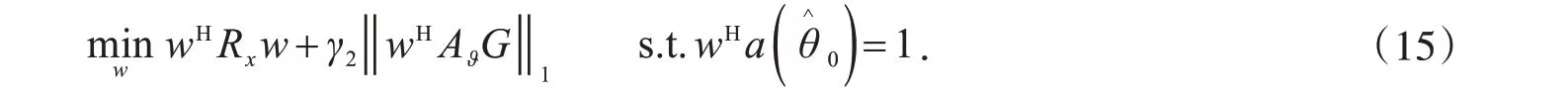
对采样信号的协方差矩阵进行特征值分解，得到信号子空间US和噪声子空间UN，因为信号和噪声是相互独立的，所以US和UN相互正交，而入射信号（包括期望信号和干扰信号）的导向矢量集合A=［a（θ0），a（θ1），…，a（θJ）］张成的子空间与信号子空间是同一个空间，所以A 与UN正交，即AHUN=0.AI⊂A，所以AIHUN=0.AI⊂Aϑ，用Aϑ的共轭转置乘以噪声子空间可以得到：

其中，AIC是Aϑ中除去AI，其余导向矢量的集合；E1是干扰信号导向矢量与噪声子空间的内积，在实际操作中，由于采样数有限，E1部分近似为0；E2为旁瓣区域中去除AI，其余导向矢量的集合与噪声子空间的内积.对E的每一行取2范数得到向量

对e中的每一个元素取倒数得到向量g，最终加权矩阵

在实际中，e1为非常接近于0 的数，g 为相当大的数，因其对应于干扰方向，相当于在干扰部位进行加权，使得干扰零陷更低.

4 仿真对比

考虑图1 所示的N 元线性天线阵列系统模型，实际应用中，对于接收端而言，期望信号和干扰信号的具体来波方向是未知的，所以要先进行DOA 估计，得到窄带信号的来波方向，设计波束成形的权值.天线阵列一旦制作完成，天线的位置发生偏移的概率不大，所以主要考虑由于期望信号的角度与估计值的误差而引起的导向矢量失配情况.

使信噪比小于干噪比，即期望信号的功率小于干扰信号的功率，采样信号的协方差矩阵Rx更接近干扰和噪声的协方差矩阵，仿真参数如表1所示.

旁瓣区域内采样间隔为1o，仿真中信号的采样数K 为100，为消除仿真实验的随机性，蒙特卡罗仿真次数为100 次，主要对比了传统Capon波束成形［5］、用l1范数约束的SCCB算法［10］和2种WSCCB算法［11-12］的性能.

4.1 无导向矢量失配的情况

假设采样数足够多，J+1个完全不相关的远场窄带信号入射到均匀线性阵列，使用DOA 估计算法得到的期望信号方向与真实的期望信号方向θ0的误差可以忽略，则期望信号的导向矢量近似等于真实的期望信号的导向矢量α（θ0）.图2 是无导向矢量失配时的天线阵列辐射方向图.从图2 来看，天线阵列增益低于于-20 dB的角度区域远大于天线阵列增益高于-20 dB的角度区域，天线阵列增益满足稀疏分布.相比标准Capon波束成形算法，其他几种改进的算法旁瓣和干扰零陷均较低，文献［11-12］算法存在干扰零陷不准的现象.图3 是输出的信干噪比随着采样数的变化图.可以看出当采样数K 增加时，几种算法的输出信干噪比均在增加，标准Capon波束成形算法信干噪比总体较小，文献［11-12］算法的输出信干噪比大致相同.

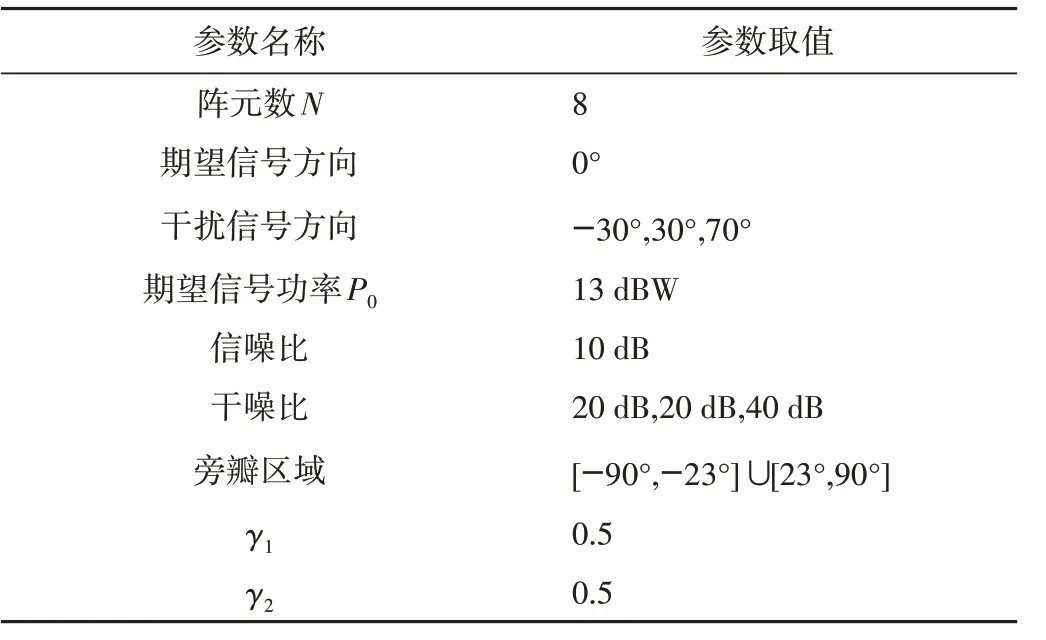
表1 仿真参数表

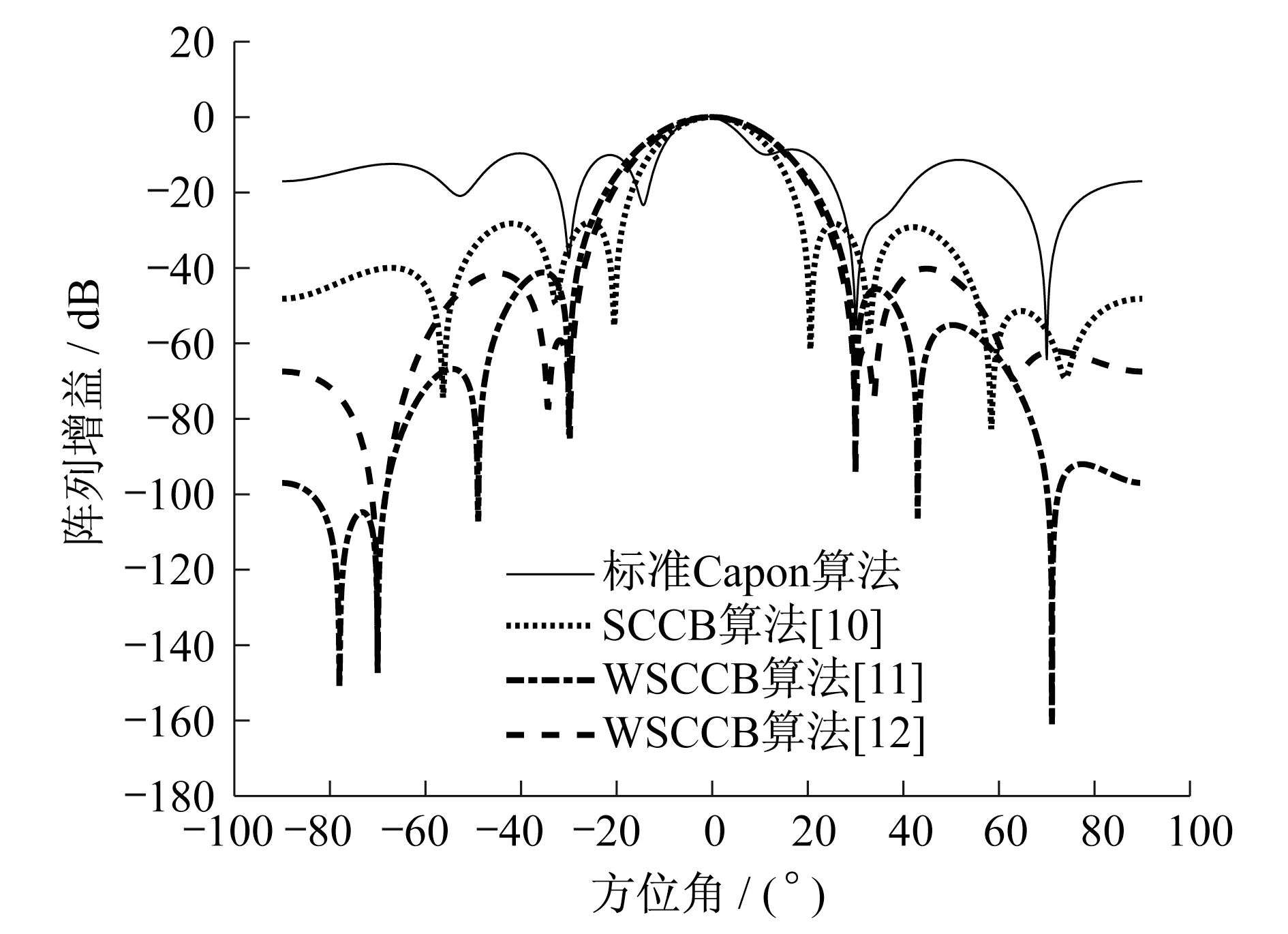
图2 无导向矢量失配的天线阵列辐射方向图

图3 输出信干噪比随采样数K的变化图

4.2 导向矢量失配时

假设DOA 估计算法由于采样数过少而导致估计的期望信号方向与真实的期望信号方向θ0存在一定的误差，造成失配问题.图4是当导向矢量存在3o失配时，4种算法的天线阵列辐射方向图对比，可以看出标准Capon 波束成形算法和文献［12］算法均把真实的0o方向的期望信号当作干扰处理，在0o处形成零陷，而文献［12］算法出现了主瓣的搬移，相比之下，文献［11］中的算法表现了较强的稳健性.图5给出了文献［12］的天线阵列辐射方向图随导向失配程度的变化图，可以看出当失配角度越大时，在真实期望信号来波方向形成的干扰零陷就越低.

图4 导向矢量存在3o失配时天线阵列辐射方向图

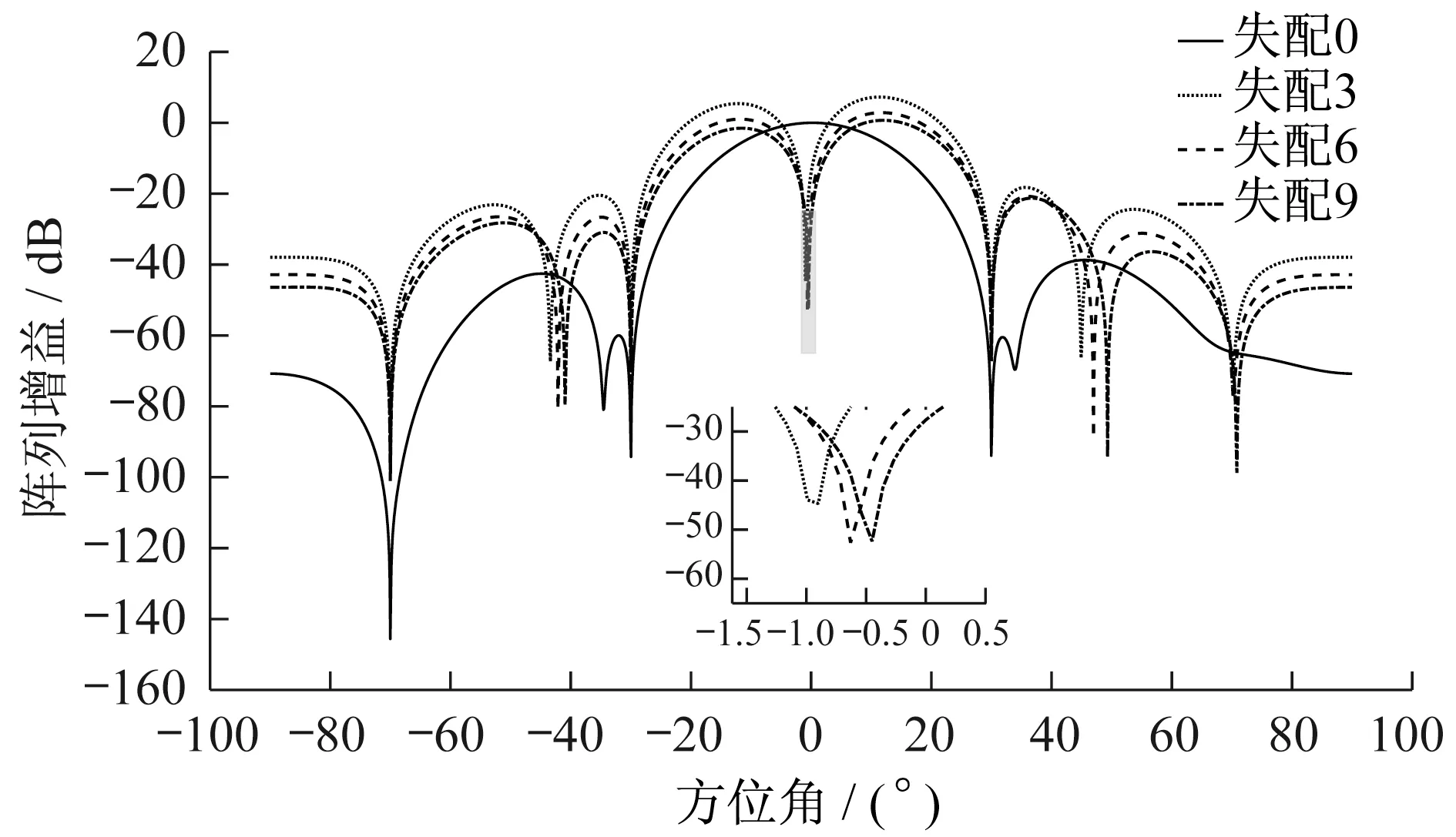
图5 天线阵列辐射方向图随导向失配程度的变化图

5 结 论

将几种加权稀疏约束的Capon 波束成形算法进行比较，仿真结果表明：相对于SCCB 算法和标准Capon 波束成形算法，两种WSCCB 算法得到的N 元线性天线阵列辐射方向图的旁瓣和干扰零陷都有一定程度的降低，但是两种WSCCB算法均存在干扰零陷，不能准确指向设定的干扰方向.如何使天线阵列辐射方向图的干扰零陷更加精准，以及进一步降低旁瓣是将来的主要研究内容.当导向矢量存在失配时，WSCCB 算法表现出了较差的稳健性，而且随着失配角度的增大，其对真实期望方向的抑制增强，所以在降低干扰零陷和旁瓣的同时，算法的稳健性也是需要考虑的问题.