基于格拉斯曼流形的多用户大规模混合预编码
2020-04-09冯湘云周小平王培培
冯湘云,周小平,王培培,汪 洋
(上海师范大学信息与机电工程学院,上海201418)
0 引 言
大规模天线系统是5G 移动通信系统物理层的关键技术之一.在多用户大规模天线系统中,基站端配置几十甚至上百根天线,同一时频的资源服务多个用户.在基站侧对发射信号进行预编码处理,可以有效降低各用户之间以及每个用户天线间的干扰[1].虽然传统的全数字预编码方法具有优良的性能,但是每根天线都需要一个专门的射频链支持运作,在大规模多输入多输出(MIMO)系统中有大量的天线阵列,成本较高[2].
为了解决全数字预编码方案中射频链路过多导致的硬件实现复杂度以及成本较高的问题,有学者提出了将数字预编码与模拟预编码相结合的混合预编码方法[3].YU 等[4]针对两种不同结构的混合预编码方法,分别提出了不同的交替最小化算法,并推广到正交频分复用调制的宽带系统中;MAJIDZADEH等[5]针对部分连接结构混合预编码方法,提出了速率最大化算法,将速率最大化问题表示为一个加权均方误差最小化问题;MAJIDZADEH 等[6]提出了3种混合预编码算法——奇异值分解匹配算法、迭代正交化算法和收发迫零算法.然而,文献[4-6]的方案只考虑了单用户MIMO系统,没有考虑多用户的场景.
格拉斯曼流形是一种特殊黎曼流形,它在最优化算法、不变子空间计算等方面有着重要的应用[7].ZHANG 等[8]和KIM 等[9]将流形应用于干扰对齐预编码中,利用流形上的最陡下降算法获得优化的发射预编码矩阵.针对多用户大规模MIMO系统,本文作者提出了一种基于格拉斯曼流形的两级混合预编码算法,预编码处理以用户接收端信号与基站发射端信号之间的最小化均方误差为准则,设计目标函数,并且将预编码矩阵在格拉斯曼流形上进行建模,利用格拉斯曼流形上的共轭梯度算法对目标函数求解,可以将复欧氏空间有约束的最优化问题转化为流形上的无约束最优化问题,从而有效降低计算维度,提高收敛速度.仿真结果表明:所提混合预编码算法的频谱效率非常接近全数字的正则化迫零(RZF)预编码算法,同时使用的射频数量大幅降低.
1 系统模型
考虑一个平坦窄带块衰落的单小区多用户大规模MIMO 系统,如图1所示,在基站侧部署均匀分布的大规模天线阵列,Nt根天线服务于K 个单天线用户,天线通过数模转换器(DAC)与nt个射频链相连接,并且满足nt=K.将所有K个用户按照空间相关性划分为S个用户簇,那么第i个簇(0≤i ≤S)中第k个用户的接收信号可表示为:

其中,(·)H表示矩阵的共轭转置;hi'k表示第i个用户簇中第k个用户的信道矩阵;ni'k表示服从复高斯分布的加性高斯白噪声;x ∈CNt表示基站经过混合预编码处理的发射信号,有

其中,xξi表示第i个用户簇的发射信号;Bξi表示第i个用户簇的混合预编码矩阵.

图1 系统模型图
2 基于格拉斯曼流形的混合预编码
2.1 基于MMSE的两级混合预编码
采用一种模拟和数字相结合的两级混合预编码方案.在第一级预编码中,将预编码分为模拟射频部分和数字基带部分,表示为



由于RZF 预编码在大规模MIMO 系统中性能较好,本研究的混合预编码算法中的数字基带部分采用RZF预编码,因此数字预编码矩阵


在第二级预编码中,为降低用户簇间干扰,以用户接收端信号与基站发射端信号之间的最小化均方误差为准则,设计的目标函数接收端的信号估计

其中,β-1是接收端的标量均衡因子.那么接收端与发射端之间的最小均方误差


假设s与n无关,那么所有s与n相乘的期望值都等于0,即

其中'tr(·)表示内积.所有用户簇的最小均方误差的期望为两级混合预编码的解,将式(6)带入式(10)可得
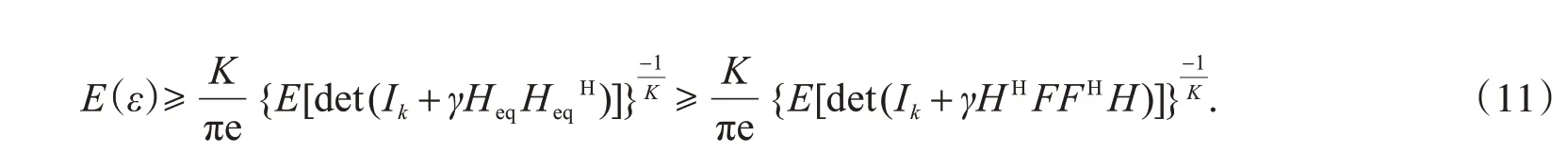
令χ(F)表示所求的目标函数,式(11)可以转化为:

由式(12)可知:对目标函数的求解实质上是求出一个射频预编码矩阵,使得目标函数取得极大值的问题.在格拉斯曼流形上建模的极大极小值问题可以等价为一个无约束的最优化问题,利用流形上的最优化算法可以对该类问题进行求解[11].
2.2 目标函数求解
流形是一个嵌入在高维欧氏空间中的光滑的曲面,格拉斯曼流形Gn'p是n维复欧式空间中的一系列p维线性子空间的集合.根据流形的定义可知,射频预编码矩阵F满足格拉斯曼流形的约束条件,在格拉斯曼流形上进行建模,表示为:

采用流形上的共轭梯度法对预编码矩阵进行迭代求解.共轭梯度法是解决大规模无约束最优化问题的一种重要全局优化方法,迭代公式如下:

其中,αi为每次迭代的线性搜索步长;di为F 在第i 次迭代时的搜索方向.在流形空间中,di由F 在第i 点的切向量表示,那么点Fi到点Fi+1的搜索方向为

其中,R(·)表示取复数的实部;⊙表示Hadamard乘积;(·)*表示矩阵的共轭.
在基于格拉斯曼流形的共轭梯度算法的迭代中,初始点的搜索方向是初始点的负梯度方向,但后面的迭代方向是Fi+1的切向量与第i+1点的负梯度Gi+1进行合并的方向,即

其中,参数r由Polak-Ribiere公式给出;流形上的梯度

其中,grad(χ(F))为目标函数在欧式空间的梯度.
3 仿真设置及结果
仿真设置为:基站端的天线Nt=256根,单天线用户数K=8,在多用户簇的情况下,把所有的用户分为S=3簇'使用Armijo回溯线搜索步长.
图2 为在Nt=256,K=8 的情况下,瑞利衰落信道中不同预编码对应的频谱效率随信噪比的变化曲线,将传统的全数字RZF预编码与本方案量化前后进行对比.图3分别仿真了全数字RZF预编码与本方案在Nt=256,信噪比分别为-10 dB,-5 dB 和0 dB 时的频谱效率随着用户数量变化的曲线.由图2,3 可知:本方案在性能上与全数字RZF 预编码方案接近,但是由于本方案使用的射频链数量与用户数量相等,远小于发射天线数量.

图2 频谱效率随信噪比的变化曲线

图3 频谱效率随用户数量变化曲线
4 结 论
针对多用户大规模MIMO 系统,使用传统的全数字预编码方案而导致硬件实现复杂度较高和实现成本昂贵的问题,提出一种基于格拉斯曼流形的两级混合预编码方案.第一级预编码中,将模拟射频预编码和低维的RZF 数字预编码相结合;第二级预编码以最小化均方误差为准则,设计目标函数,并且将预编码矩阵在格拉斯曼流形上建模,利用流形上的共轭梯度算法对目标函数求解.仿真结果表明:本算法的频谱效率非常接近全数字的RZF预编码算法,同时使用的射频数量大幅降低.
