基于NOMA系统的上行链路功率分配

梁 燕，李 莉，彭张节，符凤婷

（上海师范大学信息与机电工程学院，上海201418）

0 引 言

非正交多址接入（NOMA）系统已被公认为是第五代通信系统中较有前途的候选技术［1］.与传统的正交多址接入（OMA）系统不同，NOMA 系统通过划分功率域，同时为多个服务用户，在接收器处采用串行干扰消除（SIC）技术降低用户间干扰.

ZHANG 等［2］为了提高较低信噪比区域的NOMA 性能，提出了一种用于NOMA 系统上行链路的干扰平衡功率控制方案.ZHANG 等［3］将单小区场景扩展为多小区场景，对NOMA 系统上行链路中的用户进行随机和选择性分簇，在此基础上又分析了功率分配问题.LIU等［4］提出了一种有效的迭代算法，解决了NOMA系统上行链路的中断约束的最小-最大功率分配问题，并通过使用移位伽马分布随机变量，模拟近似用户间干扰，获得中断概率表达式.冯郑慧等［5］针对NOMA 系统下行链路簇内用户的功率分配问题，采用Karush-Kuhn-Tucker（KKT）条件进行了分析，并在不考虑解码复杂度的情况下，得出单个簇内所能容纳的最大用户数.ZHANG 等［6］将NOMA 系统下行链路能效最大化这一优化问题分解为两个子问题：1）一个非凸多变量优化问题，通过闭合表达式解决；2）一个严格的伪凹单变量优化问题，并采用二分法解决，得出了能效的最佳分配策略.LIU等［7］针对多用户NOMA系统下行链路，提出了一种新的低复杂度次优子信道分配算法，并获得了子信道复用用户之间的最优功率分配系数，为进一步改善NOMA系统下行链路的能效，提出了子信道之间不平等的功率分配（UPAAS）方案.FANG 等［8］为了最大化NOMA 系统下行链路的能效，提出了一种低复杂度的次优用户分簇算法和凸函数之差（DC）编程的功率分配算法，DC编程的功率分配算法仅对含两个用户的簇有效.ZHANG等［9］针对NOMA系统上行链路，在满足每个用户最小传输速率要求的前提下，提出了一种使频谱效率最大化的功率分配算法，并获得了用户功率分配的闭合表达式，但没有考虑对NOMA 系统上行链路能效的影响.本文作者在文献［9］的基础上，提出了一种使能效最大化的功率分配方案，相较文献［9］，本研究的功率分配方案性能较优.

1 系统模型

NOMA 系统上行链路系统模型如图1所示.基站（BS）和用户都配备有单根天线，考虑大尺度路径损耗和小尺度瑞利衰落因素，假设有M 个用户，第m 个用户和BS 之间的信道增益为hm；第m 个用户的发射功率为pm；信道中的噪声w是服从均值为0、方差为σ2的高斯白噪声.

图1 NOMA系统上行链路系统模型

根据NOMA 基本原理，多个用户同时在相同的频谱资源上向BS发送信号，并且BS已知其信道状态信息（CSI），允许对来自不同用户的发射混合信号.为了分离重叠的信号，使用了SIC 技术消除多用户干扰.不失一般性，假设M个用户的信道增益已测得且按升序排列，BS首先解码前k（k＜m）个用户的信号，剩余（M-m）个用户的信号被视为干扰，则第m个用户的传输数据速率［9］

能效η为NOMA系统上行链路的可达总速率与总功耗之比［10］，

其中，PC为用户除发射功率之外其他电路系统所消耗的总功率.

NOMA系统上行链路能效最大化的优化问题则表示为［10］：

其中，pmax为用户m 的发射功率最大限值；Rmin为用户m 的最小传输速率，式（3b）为保证用户传输数据速率满足最小传输速率的约束条件.

2 上行链路功率分配

在用户发射功率最大限值以及用户最小传输速率要求的约束下，研究NOMA 系统上行链路的能效最大化问题.通过式（2）可知，式（3）的目标函数η是非凸的分数形式，难以处理，结合式（1），NOMA 系统上行链路的可达速率

设函数

则

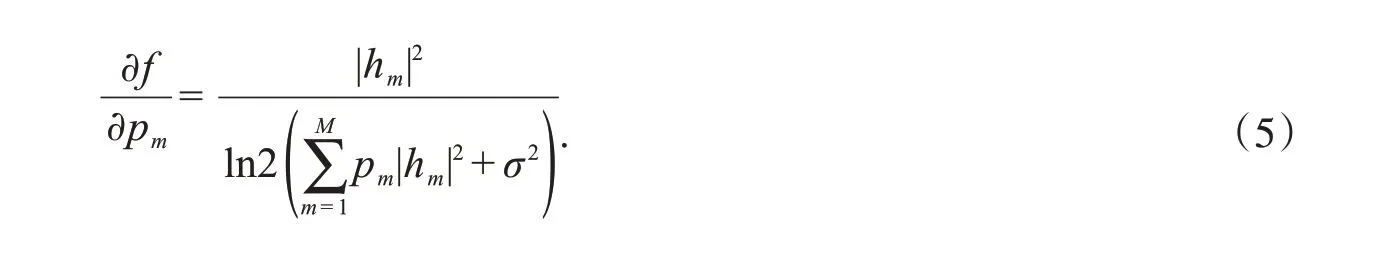
对式（5）再次求偏导，得：

因此函数f，即系统的可达速率Rsum，是关于pm的凹函数，并且系统的总功耗是仿射函数［6］，则NOMA系统上行链路的能效η属于严格的伪凹函数.

将式（1）代入式（3b）［6］，

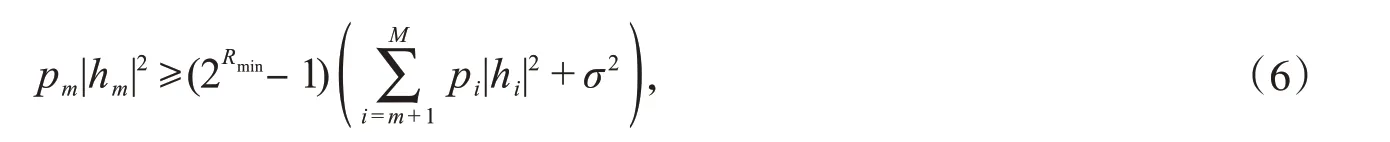
NOMA系统上行链路的能效最大化优化问题等效为：

式（7）的目标函数是严格伪凹函数，采用Dinkelbach算法［11］对其求解.

假设NOMA系统上行链路能效的最大值

则

设函数

定义式（11）与式（8）的最小误差为α，初始化能效值η=0，求出使F（0）取得最大值的一组pm，将该组pm代入式（7），求出下一个能效值η，直到函数F（η）小于或等于最小误差α，此时，η即为最优能效η*的估计值.

3 实验结果及分析

3.1 参数设置

本节通过Matlab 仿真实验验证本算法的性能.仿真环境为NOMA 系统上行链路，具体仿真参数如表1所示.

3.2 仿真结果分析

图2给出了用户发射功率最大限值从-10 dBm增大到20 dBm时能效的变化.

表1 仿真参数

图2 不同发射功率最大限值下能效的变化

由图2 可得：实验开始阶段，两种算法下，随着发射功率最大限值的增加，系统的能效均逐渐上升，这是因为发射功率最大限值对系统能效存在较大约束.当发射功率最大限值大于10 dBm时，按文献［9］的功率分配算法，系统将会继续增加功率的消耗，导致能效下降.而在Dinkelbach算法下，通过对能效的不断优化，形成最优功率分配方案，增加可用功率，不增加功率的消耗，使系统的能效趋于稳定.

图3给出了用户功率最大限值从-10 dBm增大到20 dBm时NOMA系统频谱效率的变化.

图3 不同发射功率最大限值下频谱效率变化

对比图2 和图3 可知：当用户发射功率最大限值为10 dBm 时，在本方案和文献［9］方案的NOMA 系统上行链路的频谱效率均为16.3 bit·s-1·Hz-1，但本方案系统能效提升了约15 bit·J-1·Hz-1；当用户发射功率最大限值为15 dBm 时，相比文献［9］，本方案的频谱效率降低了约1.8 bit·s-1·Hz-1，但系统的能效提升了38 bit·J-1·Hz-1.

4 结 论

研究了NOMA 系统上行链路的能效资源分配，提出了采用Dinkelbach 算法最大化系统能效的方案.仿真结果表明：当用户发射功率最大限值大于10 dBm时，系统上行链路频谱效率会降低，但能效有较为显著的提高.本研究在基站端解码时采用了理想状态下的SIC 检测技术，非理想状态下SIC 检测技术的系统能效将是下一步的研究方向.