融合Kriging算法的河套灌区ET估算方法评价

王燕鑫, 李瑞平,*,李夏子, 王思楠, 石玉芬

融合Kriging算法的河套灌区ET估算方法评价

王燕鑫1, 李瑞平1,*,李夏子2, 王思楠1, 石玉芬3

1. 内蒙古农业大学水利与土木建筑工程学院, 呼和浩特 010018 2. 内蒙古气象科学研究所, 呼和浩特 010051 3. 农牧业科技服务中心, 包头市 014500

为解决数据缺乏时对大区域ET估算的限制, 评价了融合Kriging空间插值算法的河套灌区6种ET估算方法。基于Kriging算法和气象数据, 得到7种ET估算方法的河套灌区区域ET值, 将试验站实测ET值与6种方法ET估算结果进行精度验证, 并以PM计算结果为标准, 评价融合Kriging空间插值算法的不同方法在河套灌区的估算精度与适用性, 分析不同方法与气象因子响应关系的差异性。结果表明, 综合法(KP、PVB)与PM的结果最接近, 计算结果最大偏差0.045—0.490 mm·d-1。推荐综合法为融合Kriging空间插值算法的河套灌区ET最佳估算方法, 适用于灌区所有土地类型ET估算。平均气温、温差、相对湿度较小的地区可用HS法。日照时数、平均气温、相对湿度较大的地区与风速变化较小的地区可用PT法。相对湿度较小的地区可用IA法和PVB法。

ET; 空间插值; 方法评价; 气象因子

0 前言

蒸散发(ET)是指地表水向大气传输的过程, 是陆地生态系统与大气之间水量循环和能量交换最主要的气象因子[1], 也是地表水量和热量平衡的重要参量, 包含土壤、水体和植被的蒸发蒸腾,是衡量植被生长状况和作物产量的重要指标[2]。公认最合理的ET估算方法PM[3]全面考虑影响蒸散的各种因素[4], 但在气象数据不完整的区域难以使用。因此, 简化的估算方法相继提出, 基于温度的Hargreaves-Samani[5], 基于辐射的Makkink[6]、Priestley-Taylor[7], 经验法中的Irmark-Allen[8], 综合法中的Penman-VanBavel[7]等。闫浩芳[9]对内蒙古河套灌区沙壕渠试验站的5种计算方法得到的ET结果进行适应性评价, 提出不同方法的适用条件。杨永刚[10]利用8种温度法计算中国三大灌区的ET, 根据2个气象站数据计算得到的ET结果, 推荐出适用于河套灌区计算精度较高的计算方法。王旭明[11]等选用河套灌区临河气象站1990—2012年的数据资料, 利用PM公式计算ET, 分析了ET与气象要素的关系。伴随遥感数据大量增多, 且精度逐步提高, 针对河套灌区ET模型研究有了更广泛的素材。张薇[12]2009年基于MODIS数据通过模型反演河套平原2006年日ET, 并对河套平原ET进行分析研究。杨雨亭[13]等2012年对河套平原进行双源模型估算潜在ET的对比研究, 通过假设不同的植被覆盖状况, 较为详细地比较了3种双源蒸散发模型在估算潜在ET以及区分潜在蒸发量与潜在腾发量时的模拟效果。以上研究可将ET估算方法概括为两类, 基于气象数据的普通估算模型和基于遥感数据的遥感反演模型。其中, 利用气象数据计算ET的研究均存在着以点代面的区域局限性与使用地区的特殊性, 难以推广到计算大区域ET, 且ET计算结果空间分布差异不明显。上述研究所运用的遥感反演模型中, 均存在空间或时间动态监测上的不足, 受到云量或气象条件限制, 导致部分区域无ET值。在遥感数据质量较差或云量大无法使用时, 普通ET估算方法只能分析研究单个气象站点的ET, 在范围较广及气候条件复杂的情况下, 对于分析大区域ET的时空变化情况不具有适用性及实时性, 并且计算精度较低, 而Kriging法能在一定的区域内对变量进行最优无偏估算, 对研究具有结构性与随机性的空间分布变量有独特的优点[14]。Kriging法最先考虑的是空间方位中空间属性的变异分布, 能逐点的从理论上去除预计误差, 不会有回归分析的边界效应产生[15]。在已知数据插值点较少时, 插值效果比其它方法要好, 插值数据越接近正态分布, 该法插值精度表现越优[16], 所以利用Kriging法进行空间插值往往取得理想效果[17]。

PM为目前应用最广的ET估算方法, 所以本研究以PM计算结果为参照标准, 对其它6种方法的计算结果进行精度验证和比较分析。利用气象数据计算ET的不同类别估算方法, 一般分为经验法、温度法、辐射法和综合法。本文选择IA、HS、PT、MAK、PVB、KP等6种方法估算河套灌区区域ET, 6种方法计算原理各不相同, 对ET值与气象因子响应关系的差异性分析更具有典型性。通过Kriging插值算法将6种方法得到的ET估算值进行空间插值, 提取野外实地采样点对应的PM及6种方法的ET估算值进行精度评价和适应性分析, 提出融合Kriging空间插值算法的河套灌区大区域ET最佳计算方法, 讨论不同方法与气象因子响应关系的差异性。定量计算ET对于研究区域水循环机理以及指导农业水管理具有重要意义。近年来, 随着河套灌区引水量逐年减少, 灌区水资源量已经成为制约地区农业可持续发展的首要因素。因此, 掌握灌区ET的时空分布规律, 对于计算灌区真实耗水量, 实现灌区真实节水分析, 提高用水效率, 科学指导灌区水资源合理利用和分配具有十分重要的意义。

1 材料与方法

1.1 研究区概况

内蒙古河套灌区位于巴彦淖尔的磴口县、杭锦后旗、临河区、五原县、乌拉特前旗5个地区, 东西约250 km, 南北约50 km。北依阴山山脉的狼山、乌拉山南麓洪积扇, 南临黄河, 东至包头市郊, 西接乌兰布和沙漠, 属典型的中温带季风气候, 地理坐标为: 北纬40º12′—41º18′, 东经106º20′—109º29′。灌区地形平坦, 西南高, 东北低, 海拔高度1007—1050 m, 坡度0.125‰—0.2‰。实际的灌溉面积约6.01×105hm2[9], 占总土地面积的51.2 %左右, 引黄水量占灌区总耗水量的86.6 %, 是灌区最重要的水分来源。灌区降水量少, 蒸发量大, 年平均降水量约140—230 mm, 年平均蒸发量约1900—2300 mm。夏季高温干旱、冬季严寒少雪, 无霜期短, 封冻期长, 全年以西风和西北风为主, 日温差大, 日照时间长。研究区高程及气象站位置如图1所示。

1.2 数据来源

收集处理研究区及周边2017年14个气象站数据, 气象数据主要包括日照时数、平均气压、平均气温、相对湿度、风速、日最低气温、日最高气温。其中, 5个气象站位于灌区内及边界(包括临河、磴口、杭锦后旗、五原、乌拉特前旗), 其余的9个气象站位于灌区周边(包括呼和浩特、东胜、包头、达茂旗、杭锦旗、鄂托克旗、吉兰泰、乌拉特后旗、乌拉特中旗)。灌区外的9个气象站在进行ET空间插值时, 以保证研究区边界ET的空间分布连续平滑, 减少研究区边界的ET误差。

1.3 研究方法

1.3.1 ET计算方法

用于对计算结果进行精度分析的FAO Penman- Monteith(PM)法, 是在全面考虑了影响田间水分散失的大气因素和作物因素的基础上, 把能量平衡、空气动力学参数和表面参数结合在一个对处于任何水分状态下的任何植被类型都成立的蒸发中而得到的。PM法被联合国粮农组织推荐为计算ET的标准方法, 是目前公认最准确、适用性较高的ET计算方法, 考虑了所有气象因子对ET的影响, 理论依据更为完整, 已被验证在不同区域和不同气候条件下具有较高的计算精度。6种不同类型的估算方法计算公式如表1所示。其中, Irmark-Allen(IA)法为经验法, 是Irmark和Allen等人根据美国湿润地区资料得到的拟合模型[8]。Hargreaves-Samani(HS)法为温度法, 是在美国西北部较干旱的气候条件下建立的, 仅以日最高、日最低气温和大气顶层辐射为计算参数, 比PM法更为简便, 对缺乏数据资料的地区更实用。Priestley-Taylor(PT)法和Makkink(MAK)法为辐射法, 前者以蒸发平衡理论为基础, 将空气动力学项折算为辐射值的0.26倍, 引进常数α, 导出的估算无平流条件下蒸发的模式, 利用海面和湿润陆面的资料得出α=1.26; 后者不考虑土壤热通量的影响。Penman-VanBavel(PVB)法和1972 Kimberly Penman (KP)法为综合法, 考虑多个气象因子对ET的影响。

1.3.2 Kriging空间插值算法

1951年Kriging法由南非矿山工程师克里金寻找金矿时提出并应用[18]。20世纪60年代, 法国著名统计学家马特隆对Kriging插值方法进行完善和改进, 引入了区域化变量理论, 使该方法得到深化发展[19]。克里金插值法(Kriging)以区域变化量理论为基础, 先计算样本变异函数, 再根据样本变异函数的类型选择合适的变异函数理论模型进行模拟, 最后根据模拟的变异函数对待估计点进行线性估计, 并给出估计方差作为不确定性的度量指标。利用半变异函数得到的最佳权重系数, 求得最优估计值。待估值计算公式如(1)式所示。

图1 研究区高程及气象站示意图

Figure 1 Research area elevation and meteorological station locations

表1 ET计算方法

式中:Z——待插点0的待估值;x——数据已知点的位置;——样本点的数量;0——待插点的位置;λ——权重系数, 判断已知点数据(x)对待插点数据的贡献。

基于空间结构分析, 半变异函数有效的拟合和计算, 反映了区域变化量的空间自相关性, 当区域化变量满足二阶平稳性假设和本征假设时, 半变异函数采用下式计算:

式中:()——半变异函数; h——滞后距离或步长; Z(x)——位置x的实测值;(x+)——位置(x+)的实测值;()——距离等于h的样点对数。

本文基于14个气象站的气象数据, 通过不同方法的计算公式得出7类方法ET值, 利用Arcgis软件将计算出的ET数据导入, 实现融合Kriging空间插值算法生成7种ET面状栅格数据, 从而得到整个河套灌区ET。生成的面状栅格数据比单点数据更能反映出研究区域ET时空分布与变化情况。

1.3.3 评价方法

根据典型性和全面性原则, 选取1、4、7、10月的日ET面状数据, 结合在不同土地利用类型下分布的采样点, 以PM计算结果作为标准, 提取其中相对应的6种估算方法得到的ET值, 采用均方根误差()、平均相对误差()、一致性系数()及拟合线性方程决定系数R, 对数据进行相关性分析和适应性评价。、、的计算公式如下:

2 结果与分析

2.1 不同方法计算结果分析

提取融合Kriging空间插值生成的河套灌区2017年逐月日ET面状栅格数据计算结果, 如图2所示。从图中可以看出, 夏季ET较大, 春季和秋季ET较少, 计算结果都呈现单峰趋势, 1—6月呈上升趋势, 6、7月达到最大值, 8—12月呈下降趋势, 呈现出明显的“山峰型”。PT法、IA法较PM法的ET值最大偏差分别为1.581 mm·d-1、1.921 mm·d-1, 其它4种方法KP法、PVB法、MAK法、HS法较PM法ET值偏差变化范围分别为: 0.045—0.490 mm·d-1、0.101—0.759 mm·d-1、0.170—1.070 mm·d-1、0.293—1.267 mm·d-1。根据对比以上ET值偏差范围得到整个河套灌区计算ET的方法依次为: KP法> PVB法>MAK法>HS法>PT法>IA法。

2.2 不同方法计算结果精度验证与适用性评价

2.2.1 计算值与实测值精度验证

整理临河试验地4个月逐月的日实测数据, 通过波文比能量平衡系统计算得到日ET, 与融合Kriging空间插值的7种方法得到的当月日平均ET对比分析, 评价不同方法在研究区的整体适用性。由表2中的实测值和计算值可以看出: 4个月的日平均实测ET与PM公式计算值相比, 相对误差在1.78%—17.20%之间, 均值为10.02%, 这是由于PM公式是基于气象数据计算得到的平均ET, 所以计算结果存在一定的误差。实测值与KP法计算值相比, 相对误差在3.13%—8.39%之间, 均值为6.20%。实测值与PVB法计算值相比, 相对误差在0.60%—8.37%之间, 均值为4.15%。实测值与MAK法计算值相比, 相对误差在1.92%—8.48%之间, 均值为5.89%。其中PT法和IA法误差最大, 相对误差在4.86%—31.71%之间, 均值达到20%。对比分析结果, 综合法相对误差最小, 基于辐射的MAK法较小, 其次是基于温度的HS法, 经验法IA法误差较大, PT法误差最大。不同方法相对误差对比结果如表2所示。

2.2.2 计算值与PM值精度验证及适应性评价

本文研究2017年12个月的河套灌区日ET值, 计算出的ET值具有显著的季节性变化趋势, 所以选取具有季节代表性的1、4、7、10月相对应6种估算方法的日ET值, 采用均方根误差(RMSE)、平均相对误差(MRE)、一致性系数(D)及拟合线性方程决定系数2, 与PM法计算结果进行精度对比及适用性评价。不同方法精度及指标评价结果如表3所示。

图2 不同方法ET计算结果

Figure 2 ET calculation results of different methods

表2 不同计算方法精度检验(单位: mm·d-1)

1)1月各项指标中, KP法、PVB法、MAK法均方根误差在0.179—0.259, 平均相对误差在0.256—0.371, 一致性系数在0.393—0.410, 其中KP法最优, 平均相对误差为0.256, 一致性系数达0.410, 其次是PVB法和MAK法, 两者一致性系数相接近, PVB法误差较小。其它几种方法偏离程度较大, 其中IA法计算结果平均相对误差达到0.607, 一致性系数只有0.239。

2)4月各项指标中, KP法、PVB法、MAK法均方根误差在0.411—0.540, 平均相对误差在0.109—0.148, 一致性系数在0.364—0.416, 其中KP法表现最好, 平均相对误差为0.109, 一致性系数达0.416, 其次是PVB法和MAK法, PVB法平均相对误差0.125, 一致性系数0.415, 计算结果比MAK法更为准确。其它几种方法, 偏离程度较大, IA法计算结果平均相对误差达到0.201, 一致性系数只有0.279。

3)7月各项指标中, KP法表现最优, 均方根误差0.494, 平均相对误差0.088。其它几种方法偏离程度较大, HS法、PT法、IA法均方根误差均在0.623—0.795, 其中IA法计算结果偏离程度最大, 平均相对误差0.130, 一致性系数只有0.181。

4)10月各项指标中, KP法、PVB法、MAK法、HS法均方根误差在0.407—0.494, 平均相对误差在0.168—0.221, 一致性系数在0.249—0.354。

表3 不同方法精度验证及指标评价(单位: mm·d-1)

2.3 不同方法与气象因子相关性分析

由于不同方法所考虑的气象因子不同, 同一气象因子对不同方法影响的显著程度也不同。结合图3中气象因子全年变化规律, 逐月分析5种气象因子(日照时数、平均气温、平均风速、相对湿度、温差)对不同计算方法下ET值的影响程度, 揭示不同计算方法与气象因子响应关系的差异性。从图3中可知, 日照时数1—6月逐渐增加, 7—12月逐渐减小, 夏季日照时间最长。平均气温变化趋势与ET计算结果基本一致。风速随时间变化幅度较小, 平均风速为2.56 m·s-1。相对湿度主要受到作物生长情况及浇灌影响, 在作物生长旺盛期(7、8月)和灌区秋浇期(10月)相对湿度较大。5月处于作物出苗期, 作物需水量较多, 9月大部分作物已收获且未开始秋浇, 这两个月相对湿度较小。温差变化较为明显, 初春和初秋昼夜温差大。

2.3.1 气象因子与计算方法的相关性分析

ET具有明显的季节性, 选取不同季节4个月6种计算方法得到的ET值与气象因子进行相关性分析。日照时数、平均气温、平均风速、相对湿度与不同方法计算的ET均在0.01水平(双侧)上显著相关, 温差与不同方法计算的ET随时间不同在0.05水平(双侧)上显著相关或相关性较小。6种计算方法与日照时数、平均气温及平均风速均呈正相关, 与相对湿度呈负相关, 与温差随时间不同呈负相关性或影响程度较小。综合法(KP、PVB)同时受5种气象因子影响, ET值与日照时数的相关系数变化范围0.529—0.965, 与平均气温的相关系数变化范围0.383—0.867, 与平均风速的相关系数变化范围0.365—0.905, 与相对湿度的相关系数变化范围-0.291—-0.838, 与温差的相关系数变化范围-0.129—-0.681, 与温差的相关性最差。基于辐射的MAK法除净辐射是其主要影响因素以外, 日照时数及平均风速对计算结果的影响更为明显, ET值与日照时数、平均风速的相关系数分别为0.587—0.947、0.393—0.844。基于温度的HS法受平均气温影响较为稳定, ET值与平均气温的相关系数为0.599—0.850, 表4为气象因子与融合Kriging算法的Pearson相关性对比分析。

选取相同4个月6种方法得到的灌区内未融合Kriging算法的ET值与气象因子进行相关性分析, 不同计算方法ET值与气象因子的相关系数均未通过0.01水平(双侧)置信度检验, 在0.05水平(双侧)上相关性差, 综合法与不同气象因子响应关系的差异性不明显。1月中MAK法的ET值与平均风速的相关系数为0.957, 在0.05水平(双侧)上相关性较好。4月和7月中PT法的ET值与平均气温、平均风速的相关系数分别为0.988、0.931, 在0.05水平(双侧)上相关性较好, 10月中HS法的ET值与平均风速的相关系数为0.935, 在0.05水平(双侧)上相关性较好。对比融合前后的相关系数, 融合前相关系数均未通过0.01的置信度检验, 无法有效判断不同方法ET值与气象因子响应关系的差异性。融合后的ET值与不同气象因子的响应关系通过相关系数定量表达。表5为气象因子与未融合Kriging空间插值的Pearson相关性对比分析。

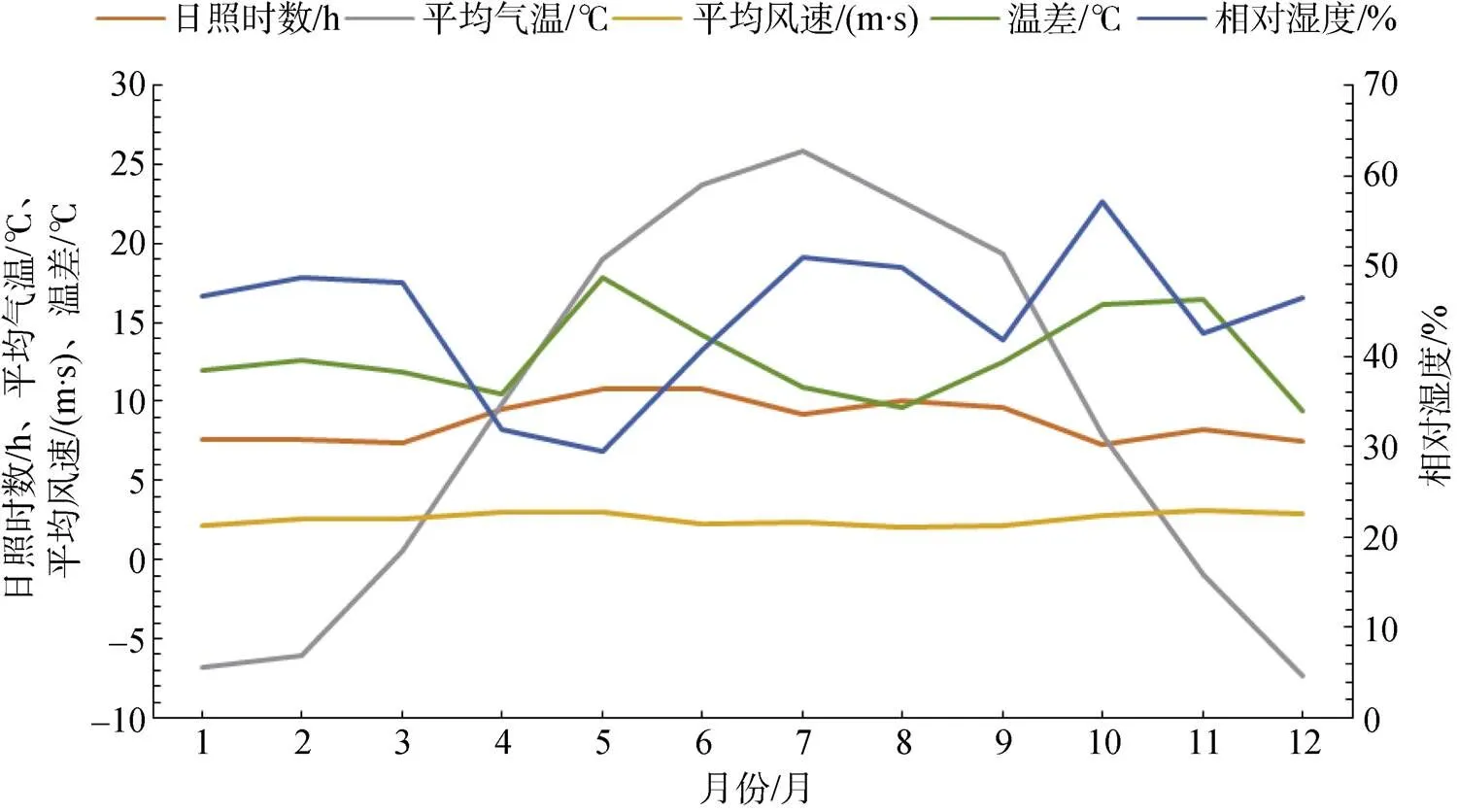
图3 气象因子年变化规律

Figure 3 Annual variation of meteorological factors

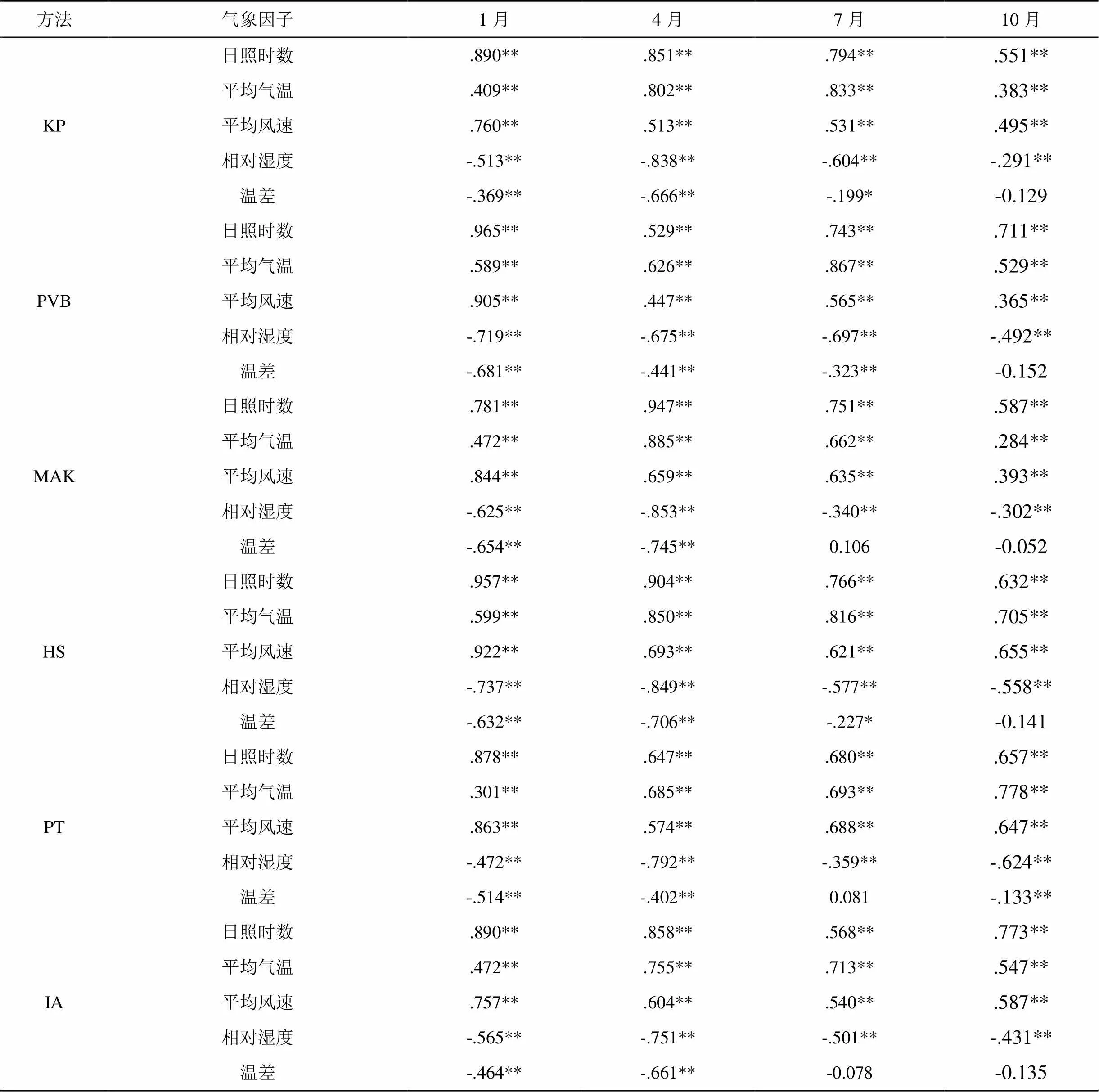
表4 气象因子与融合Kriging算法ET值的相关系数

注: **.在0.01水平(双侧)上显著相关, *.在0.05水平(双侧)上显著相关。

2.3.2气象因子与不同方法计算精度的影响分析

根据计算结果与不同气象因子的影响程度, 进一步分析4种典型方法的计算精度与气象因子之间的相关性。基于温度的HS法主要考虑平均气温和温差的影响, 平均气温与温差越小, 计算结果越准确。日照时数与风速对计算结果影响较小, 相对湿度越大, 计算结果的偏大程度也会增大, 计算精度降低。基于辐射的PT法主要考虑的是太阳辐射, 日照时数与平均气温的值越大, 计算结果精度越高。当风速变化较大时, 计算结果偏小。相对湿度增加时, 计算结果偏大, 精度会有所提高。经验法IA法受到气候、地形的限制, 仅考虑净辐射和平均气温的影响, 因此, 风速与相对湿度是该方法产生误差的主要原因, 相对湿度越大, 计算精度越低。综合法PVB法全面考虑了空气动力学项与辐射项, 克服了地形等因素的影响, 相对湿度与计算精度呈负相关, 温差越大对精度影响越大。

表5 气象因子与未融合Kriging算法ET值的相关系数

注: **.在0.01水平(双侧)上显著相关, *.在0.05水平(双侧)上显著相关。

3 讨论

本研究得出: 不同方法估算的ET均具有明显的季节性, 计算结果的变化趋势基本趋于一致。在不同时期计算结果差异不同, 6种方法在1—4月、10—12月与PM法计算结果更为接近, 5—9月计算结果差异较大。分析结果表明, 准确估算整个河套灌区ET的方法依次为: KP法> PVB法>MAK法>HS法>PT法>IA法, 这一结果与闫浩芳等[9]、杨永刚等[10]得到的结论相一致, 且变化趋势更为显著。主要原因是本研究融合Kriging空间插值算法生成的面状ET数据比单个站点ET数据更准确的反映出河套灌区整体ET变化情况, 将6种方法与Kriging空间插值算法融合前后对气象因子的差异性进行论证分析, 直观反映出不同方法在灌区的整体适用性。

4 结论

将实测数据与融合Kriging空间插值算法的6种方法ET估算结果进行精度验证, 并以PM计算结果为标准, 分析了融合Kriging空间插值算法的不同方法在河套灌区的估算精度与适用性, 论证不同方法与气象因子响应关系的差异性。综合考虑计算精度及适用性, 综合法更适合河套灌区当地气候条件下ET的估算。

1)通过提取不同土地利用类型下的102个野外实地采样点所对应的ET值, 与PM计算结果进行精度验证及适应性评价, 结果表明融合Kriging空间插值的估算结果可直观反映出不同方法在灌区的整体适用性。

2)在河套灌区气候条件下, 融合Kriging空间插值算法后的基于气象数据估算河套灌区ET最佳方法是综合法, 与PM计算结果进行对比, 综合法(KP、PVB)得到的ET估算值平均偏差范围0.045—0.490 mm·d-1, 决定系数2为0.519—0.931, 均方根误差在0.179—0.516之间, 平均相对误差在0.088—10.322之间。

3)根据不同气象因子与估算结果精度的对比分析, 在平均气温、温差、相对湿度较小的地区计算ET可用HS法。在日照时数、平均气温、相对湿度较大的地区与风速变化较小的地区计算ET可用PT法。在相对湿度较小的地区估算ET可用IA法和 PVB法。

[1] Kyotaek H, Minha C. Seasonal trends of satellite- based evapotranspiration algorithms over a complex ecosystem in East Asia [J]. Remote Sensing of Environment, 2013, 137: 244–263.

[2] 张荣华, 杜君平, 孙睿. 区域ET遥感估算方法及验证综述[J]. 地球科学进展, 2012, 27(12): 1 295–1 307.

[3] 袁小环, 杨学军, 陈超, 等. 基于蒸渗仪实测的参考作物蒸散发模型北京地区适用性评价[J]. 农业工程学报, 2014, 30(13): 104–110.

[4] Javier A, Victor H Q, Pau M. Global performance ranking of temperature-based approaches for evapotranspiration estimation considering Koppen climate classes[J]. Journal of Hydrology, 2015, 528: 514–522.

[5] 范文波, 吴普特, 韩志全, 等. 玛纳斯河流域ET0影响因子分析及对Hargreaves法的修正[J]. 农业工程学报, 2012, 28(8): 19–24.

[6] 李志. 参考作物蒸散简易估算方法在黄土高原的适用性[J]. 农业工程学报, 2012, 28(6): 106–111.

[7] PRIESTLEY C, TAYLOR R. On the assessment of surface heat flux and evaporation using large-scale parameters[J]. Monthly Weather Review, 1972, 100(2): 81–92.

[8] IRMAK S, IRMAK A, ALLEN RG, et al. Solar and net radiation-based equations to estimate reference evapotran­spiration in humid climates[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(5): 336–347.

[9] 闫浩芳, 史海滨, 薛铸, 等. 内蒙古河套灌区ET0不同计算方法的对比研究[J]. 农业工程学报, 2008, 24 (4): 103– 106.

[10] 杨永刚, 崔宁博, 胡笑涛, 等. 中国三大灌区参考作物蒸散量温度法模型的修订与适应性评价[J]. 中国农业气象, 2018, 39(6): 357–369.

[11] 王旭明, 刘海军, 张睿昊, 等. 河套灌区参考作物蒸发蒸腾量估算方法研究[J]. 干旱地区农业研究, 2014, 32(3): 95–101.

[12] 张薇, 蔺文静, 王贵玲. 基于遥感反演河套平原区域蒸发蒸腾量研究[J]. 遥感信息, 2009(6): 28–31+42.

[13] 杨雨亭, 尚松浩. 双源蒸散发模型估算潜在蒸散发量的对比[J]. 农业工程学报, 2012, 28(24): 85–91.

[14] 林忠辉, 莫兴国, 李宏轩, 等中国陆地区域气象要素的空间插值[J]. 地理学报, 2002, 57(1): 47–56.

[15] 徐翔, 许瑶, 孙青青, 等. 复杂山地环境下气候要素的空间插值方法比较研究[J]. 华中师范大学学报(自然科学版), 2018, 52(1): 122–129.

[16] 李玉霖, 崔建垣, 张铜会. 奈曼沙地春小麦蒸散量及其分析[J]. 中国沙漠, 2000(S1): 67–70.

[17] 肖城龙. 基于ArcGIS的空间数据插值方法的研究与实验[J]. 城市勘测, 2017(6): 71–73+83.

[18] PENG H L, LIU F, DUO H R, et al. The comparison of spatial interpolation methods on temperature and precipitation of Sanjiangyuan area[J]. Meteorological and Environmental Research. 2010, 1(5): 7–11.

[19] 李莎, 舒红, 徐正全. 利用时空Kriging进行气温插值研究[J]. 武汉大学学报(信息科学版), 2012, 37(2): 237–241.

[20] XYSTRAKIS F, MATZARAKIS A. Evaluation of 13 empirical reference potential evapotranspiration equations on the island of crete in southern greece[J]. Journal of Irrigation and Drainage Engineering, 2011, 137(4): 211– 222.

[21] HOSSEIN TABARI. Evaluation of reference crop evapotran­spiration equations in various climates[J]. Water Resources Management, 2010, 24(10): 2 311–2 337.

[22] AZHAR A H, PERERA BJC. Evaluation of reference evapotranspiration estimation methods under southeast australian conditions[J]. Journal of Irrigation and Drainage Engineering, 2011, 137(5): 268–279.

[23] 刘晓英, 李玉中, 王庆锁. 几种基于温度的参考作物ET计算方法的评价[J]. 农业工程学报, 2006, 22(6): 12–18.

[24] 李晨, 崔宁博, 冯禹, 等. 四川省不同区域参考作物ET计算方法的适用性评价[J]. 农业工程学报, 2016, 32(4): 127–134+316.

Evaluation of ET estimation method in Hetao irrigation district based on Kriging algorithm

WANG Yanxin1, LI Ruiping1,*, LI Xiazi2, WANG Sinan1, SHI Yufen3

1. Inner Mongolia Agricultural University, Hohhot 010018, China 2. Insititue of Meteorological Research of Inner Mongolia, Hohhot 010051, China 3. Agriculture and Animal Husbandry Technology Service Center, Baotou 014500, China

In order to solve the limitation of large-area ET estimation when data are lacking, this paper evaluated six ET estimation methods in Hetao irrigation district with Kriging spatial interpolation algorithm. Based on the Kriging algorithm and meteorological data, the ET values of the Hetao irrigation district were obtained from seven ET estimation methods. The measured ET values of the test station and the ET estimation results of the six methods were verified by the accuracy. The PM calculation results were used as the standard to evaluate the fusion Kriging spatial interpolation.The accuracy and applicability of different methods of the algorithm in the Hetao irrigation district were analyzed, and the differences in the relationship between different methods and meteorological factors were analyzed. The results showed that the comprehensive method (KP, PVB) and PM had the closest results, and the maximum deviation of the calculation results was 0.045-0.490 mm·d-1. The proposed comprehensive method was the best estimation method for the estuary irrigation area ET based on Kriging spatial interpolation algorithm, which was applicable to the ET estimation of all land types in the irrigation area. The HS method could be used in areas where the average temperature, temperature difference, and relative humidity were small. The PT method could be used in areas with large hours of sunshine, average temperature, and relative humidity, and areas where wind speed changes were small. The IA method and the PVB method could be used in areas with relatively low relative humidity.

ET; spatial interpolation; methods evaluation; meteorological factors

10.14108/j.cnki.1008-8873.2020.02.002

S161.4

A

1008-8873(2020)02-008-10

2019-07-02;

2019-09-25

国家自然科学基金项目(51769021, 51839006)

王燕鑫(1993—), 女. 呼和浩特市人, 硕士研究生, 主要从事农业水利遥感信息技术研究, E-mail: 1461287624@qq.com

李瑞平(1973—), 男. 博士生导师, 教授, 主要从事节水灌溉与农业水利遥感信息技术研究, E-mail: nmglrp@163.com

王燕鑫, 李瑞平, 李夏子, 等. 融合Kriging算法的河套灌区ET估算方法评价[J]. 生态科学, 2020, 39(2): 8–17.

WANG Yanxin, LI Ruiping, LI Xiazi, et al. Evaluation of ET estimation method in Hetao irrigation district based on Kriging algorithm[J]. Ecological Science, 2020, 39(2): 8–17.