基于专家特征的条件互信息多标记特征选择算法

程玉胜，宋 帆，王一宾，2，钱 坤

（1.安庆师范大学计算机与信息学院，安徽安庆246011；2.安徽省高校智能感知与计算重点实验室，安徽安庆246011）

0 引言

多标记学习［1］作为机器学习等领域的研究热点之一，较之传统的单标记学习中的一个对象只能局限于单个标记，多标记学习框架更具有实际性和广泛性。在真实世界中，一个对象可能隶属于多个标记［2］，此时，单个标记就难以表述对象的完整性。所以，多标记学习的研究对于多义性对象的学习建模更具有实际运用意义，近年来已成为一个新的研究热点［3-4］。

在多标记学习问题中，由于数据的高维性会引起维数灾难，导致分类器精度降低［5］。而特征选择作为一种普遍的降维手段，对于分类器的分类精度和泛化性能起重要作用。特征选择的首要目的是在样本数据集中找到一个特征子集，且使得找到的特征子集蕴含尽可能多的区分类别信息，同时要考虑子集内部的冗余性尽量小［6］。而信息论中的互信息理论，作为不确定性的一种有效度量方式，被广泛用于多标记特征选择，因此许多学者在此方面进行了研究。例如Zhang等［7］提出的基于最大相关性的多标记维度约简（Multi-label Dimensionality reduction via Dependence Maximization，MDDM）算法。Lee 等［8］通过多元互信息最大化已选特征与标记集合的相关性，提出了基于多变量互信息的多标记特征选择算法PMU（Pairwise Multivariate mutual information）。Lin 等［9］提出了基于邻域互信息的多标记特征选择。刘景华等［10］通过互信息排序已选特征和标记的相关性，提出了基于局部子空间的多标记特征选择算法（Multi-label Feature Selection algorithm based on Local Subspace，MFSLS）。

上述算法的多标记特征选择算法判定特征是否冗余的标准单一，如信息熵方法仅考虑特征和标记间的相关性，未考虑特征和特征间的关系［11］；联合互信息虽然考虑了整体互信息大小，但未考虑单个特征和标记间的相关性。这些算法都没有提取关注专家特征，在整个特征集中进行特征选择，因此时间复杂度很高，如PMU 算法在大数据集中执行时间很长，基于信息熵的多标签特征选择（Multi-Label Feature Selection based on Information Entropy，MLFSIE）算法虽然提高了执行速度，但未考虑特征间的冗余性。

除此之外，包括上述算法在内的大多数多标记特征选择算法均未考虑到优先挑选出专家特征的现实意义，忽略了一个关键的问题：在现实生活中，人们针对分类问题时，通常根据专家经验选取几个或者多个最重要的特征，然后再通过相关评价准则建立特征向任务目标的映射进行多标记分类。例如，在医院中专家医师看病人的病情时，往往根据自己的多年临床经验先确定几个最重要的病症（即对结果不可或缺起到重要作用的特征（专家特征）），然后再在专家特征的基础上进行各种身体检查、血液化验、分析病历，最后分析汇总来确诊。同时也要考虑某些看似不显眼的症状（即与标记空间相关性较弱的特征），因为忽略某些重要性较次要的特征也会产生误诊的可能。

基于此，再结合信息论中的互信息［12-14］，本文提出一种基于专家特征的条件互信息多标记特征选择算法（Multi-label Feature Selection algorithm based on Conditional Mutual Information of Expert Feature，MFSEF）。该算法在最小冗余最大相关性前提下，通过子空间划分，考虑了重要性较次要的特征可能对分类性能产生的影响，受现实生活中实际问题的启发，兼顾考虑了可能决定整体的预测方向的专家特征，从而提升多标记分类性能。首先通过瀑布图联合互信息选出几个最关键的专家特征；再以该专家特征作条件，保持专家特征不变，与余下的特征作并集，构建融合一个新的特征空间，然后计算新特征与标记集合之间的互信息，再进行排序形成新的特征排序集合；借鉴MFSLS 的思想，最后进行特征选择。实验在7 个多标记数据集上测试，同其他常用的多标记特征选择算法进行比较，通过4 个评价指标的结果可以看出，本文算法优于通用的多标记特征选择算法。最后，还通过统计假设检验进一步证实了本文方法的合理性与稳定性。

1 理论介绍

1.1 多标记学习

由于真实世界的对象具有多义性，多标记学习框架作为一种多义性对象学习建模工具由此产生［15］。在该框架下，每个对象由一个示例描述，每个示例具有多个但有限的类别标记，学习的目的是为每个未知示例赋予正确的标记。在数学语言中，多标记问题可描述为：假定X={x1，x2，…，xn}Τ∈Rn*d表示有n 个样本且每个样本特征维度为d，Y={1，2，…，Q}表 示 样 本 对 应 的 标 记 集 合［16］。T={(x1，Y1)，(x2，Y2)，…，（xm，Ym）}（xi∈X，Yi∈Y）表示训练集，多标记学习目的是得到映射关系f：X →{-1，1}Q，从而对新样本进行标记的预测。

1.2 条件互信息

定义1设集合A={a1，a2，…，am}，令p(ai)表示元素ai的先验概率，则集合A的信息熵为：

信息熵可以度量集合不确定性的程度，信息熵越大表示集合的不稳定性越大。对于多标记特征选择算法，常通过信息熵来选择特征空间中与标记空间互信息较大的特征。

定义2设集合A={a1，a2，…，am}，B={b1，b2，…，bn}，则在给定集合A的条件下集合B的条件熵为：

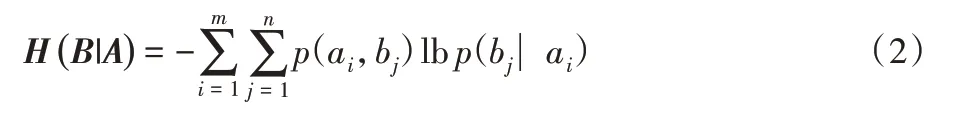
条件熵可以度量在集合A 出现的条件下集合B 的不确定程度的大小。

定义3设集合A={a1，a2，…，am}，集合B={b1，b2，…，bn}，则集合A与B的联合熵为：

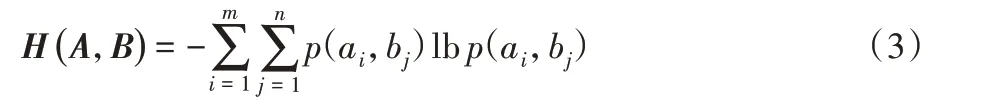
信息熵、条件熵及联合熵的关系为：

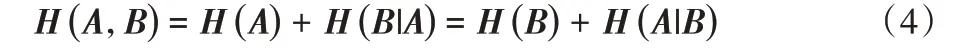
定义4给定集合A 和集合B，定义集合A 和B 之间的互信息为：

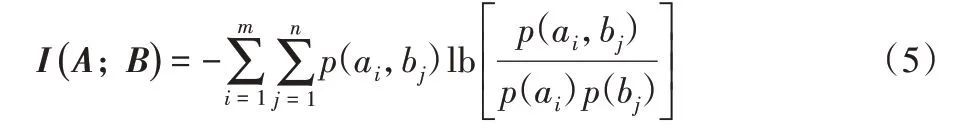
互信息被广泛用于度量随机变量间相关性的大小，即I(A；B)表示集合A 和集合B 间的相关性大小。I(A；B)越大，表示两者间的相关性越大。另有I(A；B)=I(B；A)，且满足：

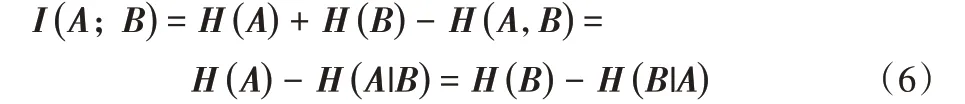
当I(A；B)=0 时，集合A 和集合B 无相关性，集合A 和集合B之间未提供任何信息。

定 义5设 集 合A={a1，a2，…，am}，B={b1，b2，…，bn}，C={c1，c2，…，ct}，则在集合C 条件下集合A 和B 间的条件互信息［17］为：

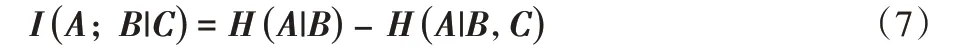
联合互信息可由式(6)和式(7)得出：

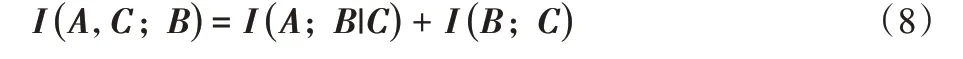
联合互信息是考虑A、C 整体同B 之间的关系，由上式可知条件互信息和互信息之和为联合互信息，根据式（5）得出联合互信息为：

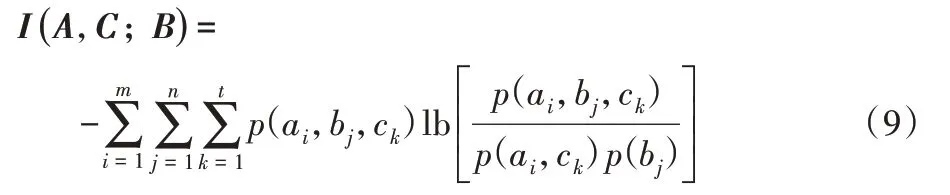
联合互信息I(A，C；B)越大，则表示A、C 整体同B 间的相关性越强。另外关于条件互信息还可变形表示如下：

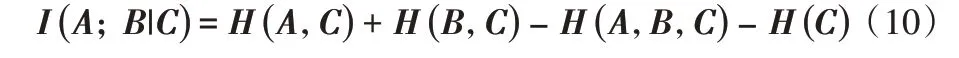
2 MFSEF

在通过互信息考虑特征与标记之间的相关性来进行多标记特征选择中，先给定f表示描述样本的特征，l表示样本的类别标记，则I（f；l）虽然仅可以在单标记中描述在样本中特征和类别标记之间的相关性程度，而在多标记中，一个样本是由多个特征向量表示且隶属于多个类别标记，故给出以下定义。

定 义6给 定 特 征f 和 标 记 空 间L={l1，l2，…，ln}，为特征f 和标记li的互信息，那么特征f和标记空间集L的互信息可定义为：

定义7给定一个特征子集为S={f1，f2，…，fm}，特征fi与特征子集空间的互信息定义为：

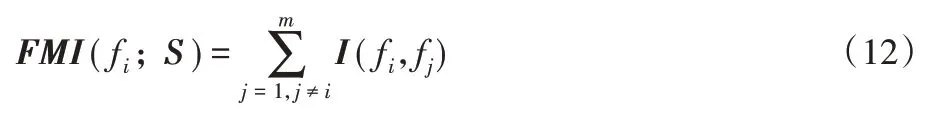
特征与标记集合之间的互信息大小描述了两个集合间的相关性程度，特征和标记集合的互信息越大，表明该特征越重要；反之，表明该特征重要性越弱，当特征和标记集合的互信息为零时，表明该特征和每个类别标记相互独立，此时特征和标记集合的互信息也取得最小值。

给定训练样本U={x1，x2，…，xn}和其构成样本的特征集合F={f1，f2，…，fd}，以及标记空间集合L={l1，l2，…，lt}。

由于专家特征在现实生活中是通过人的经验主观性选定，而本文实验所采用数据集为常用的多标记数据集，若单纯地人为指定专家特征，可能会影响实验的可靠性和有效性，故可事先通过数据集画出对应的特征值瀑布图，然后根据瀑布图联合互信息理论挑选出几个特征作为专家特征。图1 和图2为常用多标记数据集所画的部分代表性瀑布图。

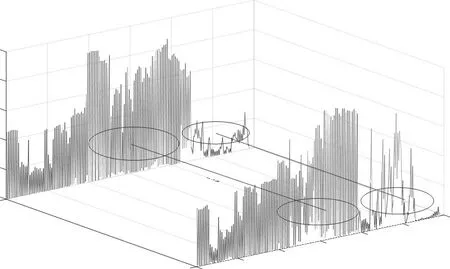
图1 第600和601个样本中所有特征对应的特征值构成的瀑布图Fig.1 Waterfall plot of eigenvalues corresponding to all features in the 600th and 601th samples

其中图1 展示了在第600 个样本到第601 个样本中，每个特征所对应的特征值大小的对比，由图可看出：两个样本对应的前100个特征的特征值基本较小且小于0.5，两样本特征值基本相同，表明该段特征对标记的影响甚微；而在第200 到300 之间的特征所对应的特征值数值有大有小，分布极其不均衡，波动较大，说明该段特征对样本类别的划分起到决定性作用，即称隶属特征；在第100 和200 之间的特征所对应的特征值基本数值较大，且分布均衡，无较大波动，表明该段特征对标记的影响至关重要，即称为专家特征。

在图2 中展示了在所有样本中，每个特征所对应的特征值大小的对比。针对100～200 的专家特征，明显看出所有样本的特征值基本较大接近1，这表明这部分特征对于标记的划分不可或缺，但这部分特征值基本相同，表明全部样本基本上均具有该特征，所以如果事先把这些特征挑选部分出来，作为条件与剩余特征相联合，然后再针对剩余特征进行后续特征选择操作，无疑可以避免重复计算，提高特征选择速度，而且更符合现实生活中面对分类问题时，常优先选出专家特征的操作习惯，因此更具有实际应用价值。

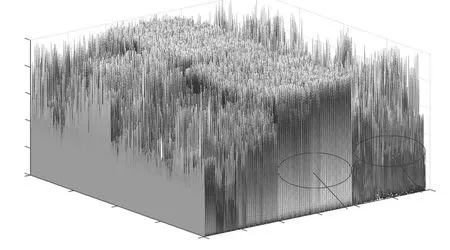
图2 全部样本所有特征对应的特征值构成的整体瀑布图Fig.2 Overall waterfall plot composed of eigenvalues corresponding to all features of all samples

先通过瀑布图观察出专家特征的大致分布，再通过互信息考虑特征空间和标记空间的相关性大小，由互信息大小降序挑选靠前的特征，最后综合考虑两要素选出若干个特征作为专家特征。本文实验取前四个特征作专家特征，记作E={e1，e2，e3，e4}。

传统的基于互信息的多标记特征选择算法仅考虑特征空间F 与标记空间L 的相关性：F →L，本文以专家特征E 为条件，保持专家特征不变，将专家特征和每个原始特征作并集构建新的特征空间，再考虑其与标记空间的相关性：E ∪F →L。

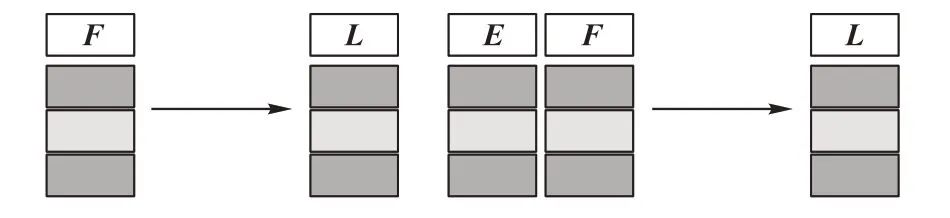
图3 专家特征联合的图解描述Fig.3 Graphical description of combining expert features

由定义6 可知特征和标记集合的互信息越大，表明该特征越重要；反之，表明该特征重要性越弱。故用互信息大小进行降序排列得到一组新的特征序列：

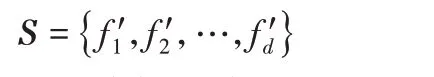
对于多标记特征选择，由于每个标记隶属于不同特征空间，因此对于特征和标记集合的相关性通过互信息大小进行计算时，相关性强的特征之间可能有比较大的冗余性，而相关性弱的特征也不一定对判别标记类别不起作用，也有可能某个相关性弱的特征往往对最后分类结果起决定性作用。考虑到此情景，可以通过建立局部子空间模型来解决此问题［10］。文献［18］中说明，当数据集的特征维度较小的时候，子空间个数可以划分2、3、4，考虑到较多保留相关性强特征，同时兼顾对某些类别标记贡献较大的但是特征与标记相关性较弱的特征，故每个特征子空间的采样比例可以设置为由大到小，例如对于2 个子空间，采样比例可为：｛0.6，0.4｝、｛0.7，0.3｝、｛0.9，0.2｝。又由文献［10］中实验证明3 个子空间的预测效果最好，故可以将已经通过专家特征进行互信息大小降序排列后的特征序列划分为三个子空间，再通过｛0.6，0.3，0.1｝的采样比例进行进一步的特征选择。

局部子空间的详细过程如下：

给定有d 维特征空间，三个子空间，故每个子空间特征维数为，由定义6 可计算出在子空间中每个特征和剩余特征的互信息大小：此时互信息越大，表明其特征的冗余性越高；反之，特征间互信息越小，冗余性越低。因此将通过定义6 新得到的三个子空间中的特征进行升序，三个子空间关于特征间的冗余性排列分别为：

再通过采样比例分别在三个子空间中选择冗余性比较小的特征，由于采样比例为｛0.6，0.3，0.1｝，故三个子空间通过比例选择出的特征个数分别为：

模拟现实世界中分类问题，引入专家特征作为条件，同原始特征作并集，通过信息论中的互信息理论背景，计算特征与标记空间的相关性大小，再结合局部子空间模型的划分，最后实现特征选择。这样既考虑了多标记特征选择在现实社会中的合理性和实用性，也避免了传统特征选择只是根据相关准则选择较强的特征导致的特征间的冗余性，最后实验结果也显示了较好的分类性能。

算法1 MFSEF。

输入 多标记数据集D，专家特征E；

输出 特征子集Sub。

2） E={e1，e2，e3，e4}；

3） for each fi∈L

5） for each lj∈L

6） 通过定义6计算FMI(fi∪E；lj)

7） end

9） end

10）通过第8）步计算出来的特征空间和标记空间互信息大小，对特征进行一个降序，从而得到新特征序列S；

11）将特征集合S均分成3个子空间S1、S2和S3；

12）对三个子空间分别通过定义7 计算特征和特征的互信息大小，然后进行升序排列，再通过采样比例｛0.6，0.3，0.1｝在三个子空间分别挑选出新的特征子集；

13）将四个专家特征和新得到的三个特征子集合并，按顺序依次放入Sub。

3 实验及其结果分析

3.1 实验数据集

为验证本文算法的有效性，选取了Entertainment、Recreation、Artificial、Reference、Health、Business、Computer共7个数据集，详细信息见表1。

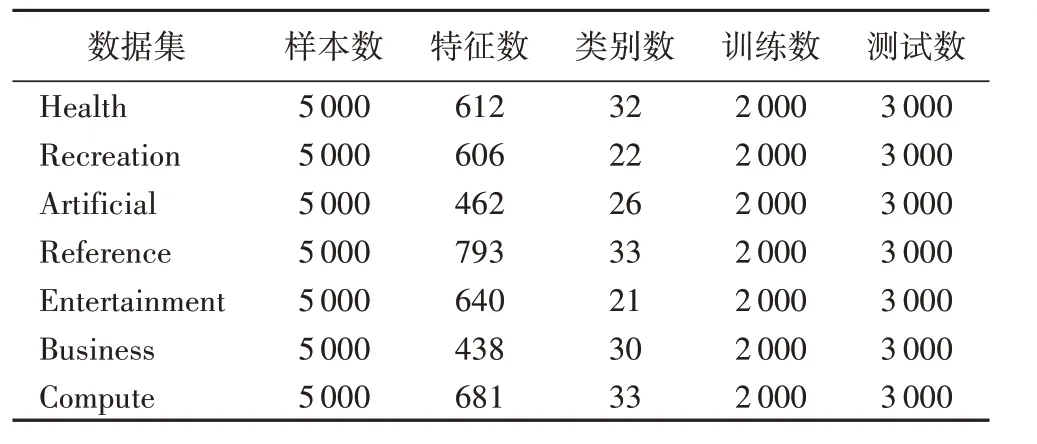
表1 多标记数据集Tab.1 Multi-label datasets

3.2 实验环境及评价指标

本实验代码在Matlab 2016a 中运行；硬件环境为Intel Core i5-2525M 2.50 GHz CPU，8 GB 内 存；操 作 系 统 为Windows 10。实验选取多标记常用的4种性能评价指标［19-20］，即平均精度（Average Precision，AP）、海明损失（Hamming Loss，HL）、排序损失（Ranking Loss，RL）和1-错误率（One Error，OE）来综合评价多标记学习算法性能，且分别简写为：AP↑、HL↓、RL↓和OE↓，其中：↑代表指标数值越高越好，↓代表指标数值越低越好。设：多标记分类器h(⋅)，预测函数f(⋅，⋅)，排序函数rankf，多标记数据集D={(xi，Yi|1 ≤i ≤n)}。上述4种评价指标AP、HL、RL和OE形式化定义如下：

1）Average Precision：评估在特定标记y ∈Yi排列的正确标记的平均分数。

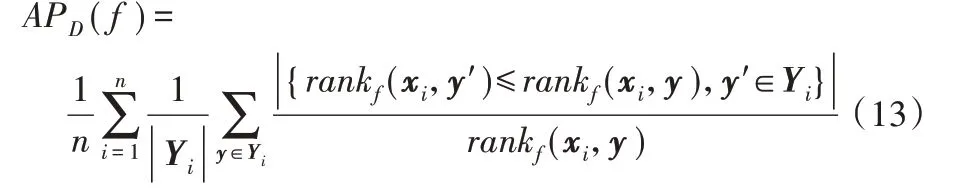
2）Hamming Loss：用于度量样本在单个标记的真实标记和预测标记的错误匹配情况。

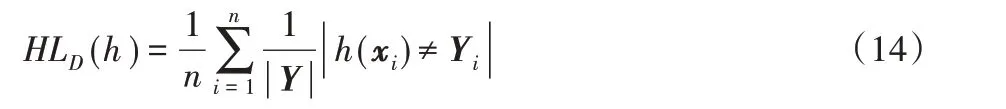
3）One Error：评估对象最高排位标记并未正确标记的次数情况。

4）Ranking Loss：用来考察样本的不相关标记的排序低于相关标记的排序的情况。

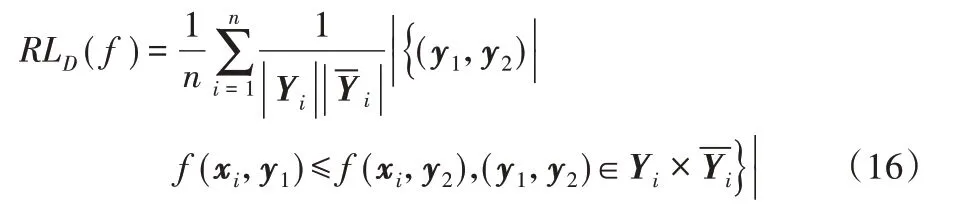
3.3 算法选择与相关参数设置

为验证新提出的特征选择算法性能，实验将MFSEF 算法与4 个经典多标记特征选择算法进行对比，分别是MDDMspc、MDDMproj、PMU及MFSLS。表2到表5中的第2列Original 表示在原始特征空间下仅通过基本的经典多标记分类器ML-kNN 的分类性能；MDDM 是基于最大相关性的多标记维度约简算法，而MDDM 又可划分为MDDMspc 和MDDMproj，PMU是通过多元互信息最大化已选特征与标记集合的相关性，提出基于多变量互信息的多标记特征选择算法。其中MDDMspc 和MDDMproj 算法需先进行原始数据归一化，再进行特征选择，MFSLS 和PMU 是针对离散型数据进行处理，鉴于此，为了实验的严谨和合理性，以MFSLS和PMU 离散化方法为基准，对本文实验数据先两折离散化。由文献［18］可知，当选择多标记数据集的特征维度不高时，将子空间划分为3 个，特征采样比例设置为｛0.6，0.3，0.1｝，专家特征个数k_1 设为4。另本实验最后分类器采用ML-kNN，故相关参数选择默认值，近邻个数k取10，平滑参数s取1。

3.4 实验结果

表2到表5给出了本文算法和其他4种算法在7个多标记数据集上实验结果，最好的结果加粗表示；同时，每种方法在所有数据集上的平均排序结果列在最后一行；数据右下角括号数字表示6种算法分别在评价指标下的排序序号。

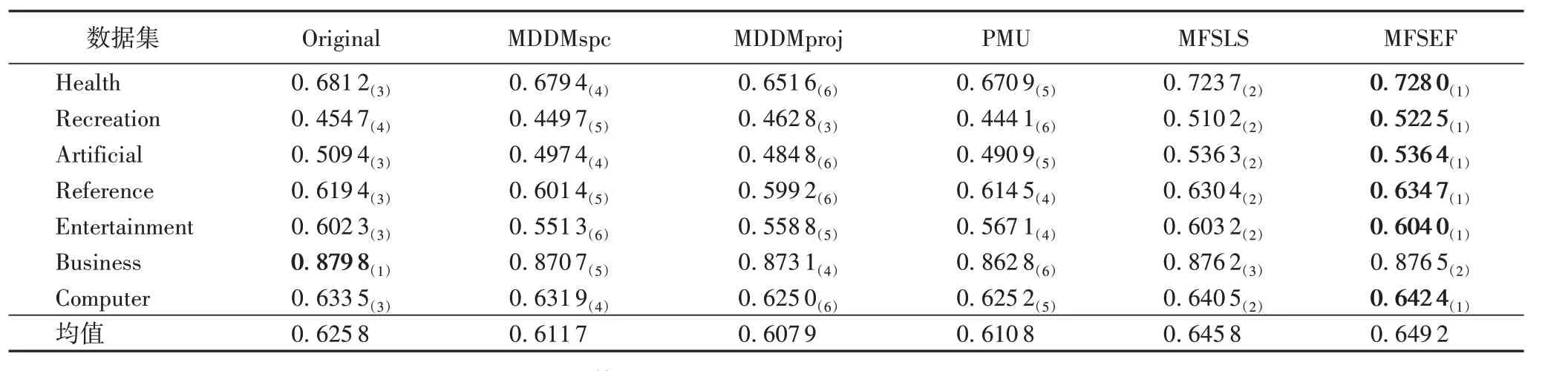
表2 各算法在7个数据集上的平均精度测试结果Tab.2 AP（↑）results of each algorithm on 7 datasets

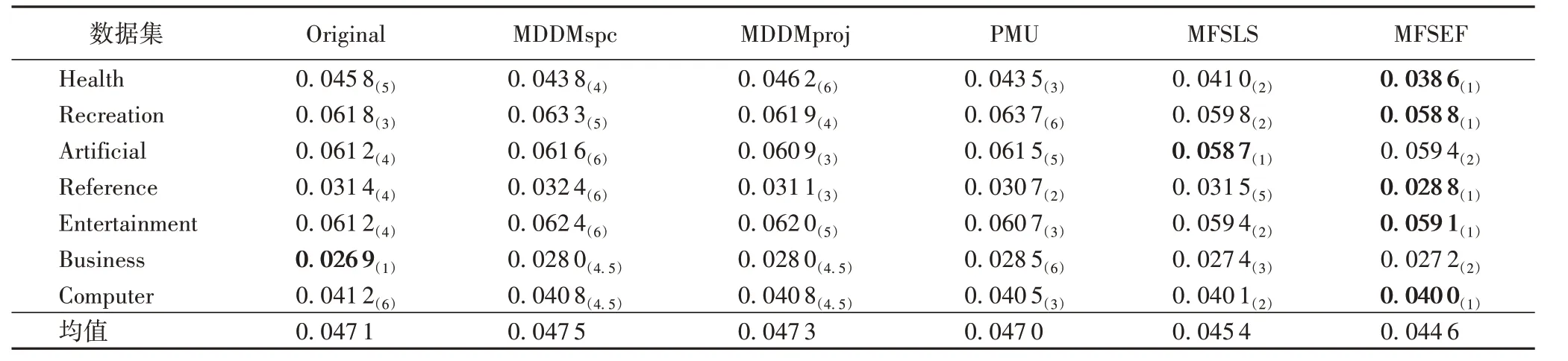
表3 各算法在7个数据集上的海明损失测试结果Tab.3 HL（↓）results of each algorithm on 7 datasets

表4 各算法在7个数据集上的排序损失测试结果Tab.4 RL（↓）results of each algorithm on 7 datasets

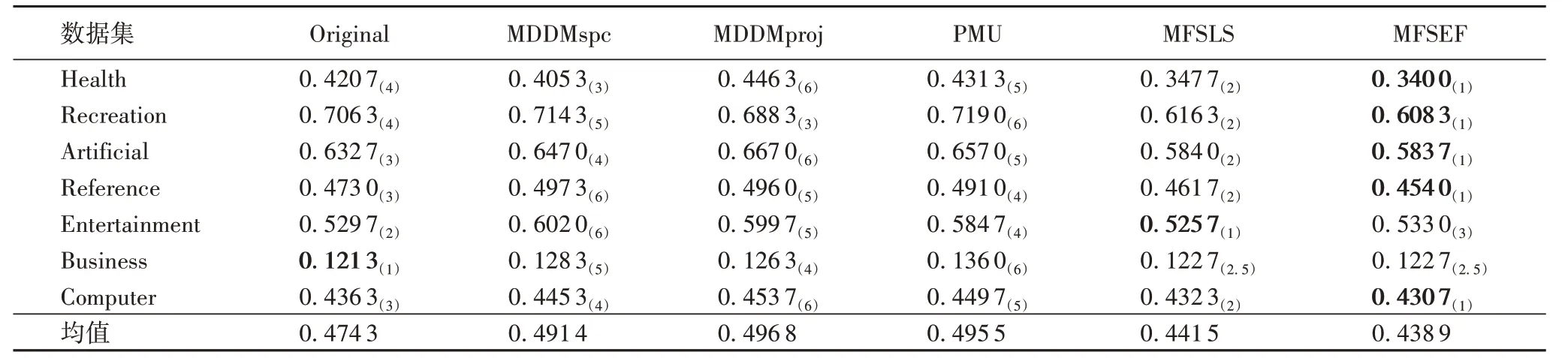
表5 各算法在7个数据集上的1-错误率测试结果Tab.5 OE（↓）results of each algorithm on 7 datasets

实验结果显示：MFSEF 在Health、Recreation、Artificial、Reference、Entertainment、Business、Computer 等7 个多标记数据集上实验结果的平均排序都占优，其中，对于AP指标，平均数值越大，算法性能越优，对于其他三个评价指标，平均数值越小，算法性能越优。从表2到表5可发现：

①在AP 指标中，MFSEF 仅在Business 数据集中AP 不是最优，排名第二。对比4种算法和原始特征空间，MFSEF 在其他数据集中AP值最大，即分类性能达到最优。

②在HL指标中，MFSEF 在Business和Artificial数据集中HL 值排名第二，对比4 种算法和原始特征空间，MFSEF 在其他数据集中HL值最小，即分类性能达到最优。

③在RL指标中，MFSEF在Health和Business数据集中分别排第二和第三，在其他5个数据集对比4种算法和原始特征空间，MFSEF的RL值最小，即分类性能达到最优。

④在OE 指标中，MFSEF 在Entertainment 数据集上排第三，在Business数据集和MFSLS对比算法并列排第二，在其他5 个数据集对比4 种算法和原始特征空间，MFSEF 的OE 值最小，即分类性能达到最优。

上述实验分析充分表明，通过本文算法特征选择后的特征子集在后续分类性能上，对比其他4 种算法和原始特征空间在7 个多标记数据集中多数占优，验证了本文算法的有效性和鲁棒性。

图4是对比其他4种算法，随着选择后的特征数目的逐渐变多，其分类性能的变化情况。针对每一种算法，都有28 种对比结果。介于篇幅所限，本文只选取了Artificial 数据集的曲线图进行分析，分别展示了在AP、HL、RL和OE四种评价指标时，5 种算法在特征数逐渐变大时分类性能的变化情况。对比原始特征空间和PMU、MDDMspc、MDDMproj、MFSLS 这4种算法的分类性能，在Artificial 数据集上，MFSEF 基本上占优。基本上在前80 个特征范围类，本文算法在四个评价指标上均明显优于其他对比算法，并且往往能通过较少的特征数更快地达到更好的分类性能。另外，在其他未展示的数据集上，本文算法的分类性能曲线变化也多数占优，这充分地表明MFSEF的有效性和合理性。

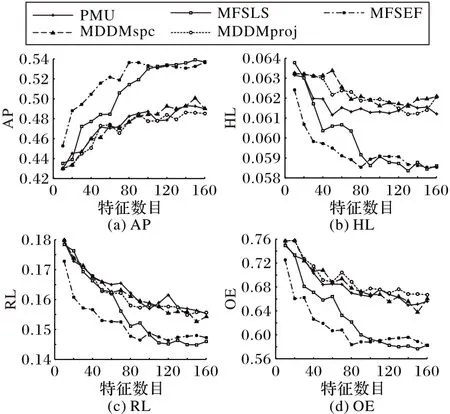
图4 Artificial数据集的各个评价指标的性能变化Fig.4 Changes in performance of various evaluation indicators on Artificial dataset

3.5 统计假设检验

在上述实验分析中，本文算法达到了显而易见的效果，下面将运用统计学中统计假设检验［21］进一步说明本文算法的有效性和合理性。

统计假设检验：在上述7 个数据集上采用显著性水平为5%的Nemenyi 检验［22-23］来对比MFSEF 算法与其他对比算法。如果两个算法在所有数据集上的平均排序的差值小于或者等于临界差值（Critical Difference，CD），那么这两个算法之间没有显著性差异，反之存在显著性差异。如图5 所示，在最上行为临界值CD=2.850 0时，若两个算法之间没有显著性差异则用实线连接。在图5 中，随着坐标轴上的数值增大其算法性能依次降低。

图5 展示了各算法在AP、RL、HL、OE 四个指标上的CD图，从中可以看出，本文算法在4 个指标上性能均处于首位。具体在平均精度指标上，如图5（a）、（b）、（d）所示，在Average Precision、Ranking Loss 和One Error 三 个 指 标 上，MLSEF 与MDDMspc、PMU、MDDMproj 均有显著差异，且优于这三种算法；如图5（c）在Hamming Loss 指标上，本文算法与MDDMproj和MDDMspc有显著差异，且优于这两种算法。与其他算法相比，在统计上，本文算法有45%的概率与其他算法无显著性差异。

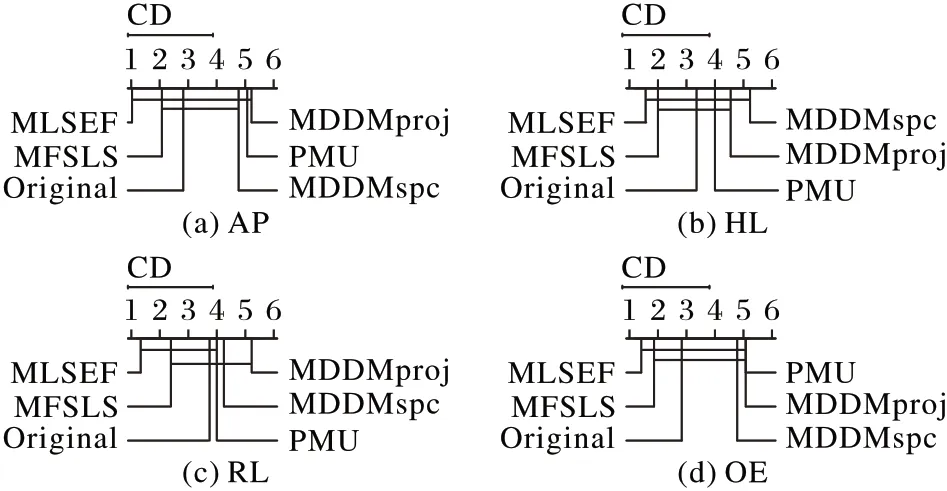
图5 算法综合性能比较Fig.5 Performance comparison of algorithms.

通过以上针对图5 的分析，可知本文算法综合性能最为优秀，在统计上也优于其他对比算法。基于以上的实验结果和统计分析再次充分表明本文算法的优越性。

4 结语

与通过相关准则挑选特征和标记相关性强的多标记特征选择算法相比，本文不仅考虑了重要性较次要的特征可能对分类性能产生的影响，还考虑了可能决定整体预测方向的最关键特征。模拟现实生活中的实际情况，通过经验优先挑选出部分专家特征与剩余特征相联合，利用条件互信息和联合互信息理论得出一个与标记集合相关性由强到弱的特征序列，再通过划分子空间去除冗余性较大的特征，最后保留专家特征和挑选出的新的特征作为最后的特征子集。在已公开的多个基准多标记数据集中的实验结果表明，该算法在实验中较其他对比的多标记特征选择算法有一定优势和较好的稳定性，且更具有实际应用价值。

本文算法在专家特征的选取上还可以进一步探讨，目前只是通过瀑布图联合互信息理论模拟选出几个专家特征，所以最后结果可能由于个人选取专家特征的不同，实验结果和预期效果存在一定的误差，但是针对具体问题分析数据，合理选择专家特征，还是可以有效减少误差。