基于ALE方法的弹性圆柱壳入水时的流固耦合模拟
2020-04-09施红辉温俊生贾会霞
施红辉,周 栋,温俊生,贾会霞
(浙江理工大学 机械与自动控制学院,杭州 310018)
海上作战能力是一个国家军事强弱的重要体现,是维护国家主权的重要保障。因此,超空泡技术应运而生,国际上涌现出很多超空泡应用技术,比如俄罗斯超空泡鱼雷“疾风”,美国海军作战中心采用超空泡作战技术设计的“适应高速水下弹”的射弹,这些超空泡减阻技术得到了广泛的军事应用[1]。此外,物体撞击水面时会遭受到巨大的冲击载荷,严重影响其弹道稳定性甚至引起结构破坏。因此,物体入水问题的研究对于解决鱼雷、反潜导弹、破障炮弹的入水运动问题具有至关重要的意义[2]。
1929年,Von Karman[3]最早提出了平板撞水问题的渐进理论,该理论基于线性化自由表面和体边界条件。1932年,Wagner[4]对Von Karman的公式在考虑“水堆”效应的前提下进行了修改。到了2004年,Aquelet等[5]通过有限元方法预测了楔形体撞击水面时的局部脉冲载荷。Khazraiyan等[6]基于ALE方法,模拟了低速射弹的入水过程,得到了射弹入水过程中压力的变化以及射弹速度与加速度随着入水时间的变化。孙琦等[7]采用ALE方法,对三维弹性弹丸的撞水过程进行了流固耦合模拟。康德等[8]采用ALE方法,模拟得到了三维长方体破片在水介质中高速运动时的速度衰减规律、墩粗变形规律以及冲击波传播过程。段宇等[9]通过具体的实验图像分析发现低速圆柱壳入水之后受到的阻力具有明显的不同,大致规律是:平头圆柱壳受到的阻力最大,其次是圆锥圆柱壳,而圆球头圆柱壳受到的阻力最小。这一规律对相关研究具有很好的借鉴性。路中磊等[10-11]先是做了开放腔体圆柱壳的入水实验,而后又进行相关数值计算,其进行的对比研究发现,入水速度对空泡的流动规律具有关键的影响,开放腔体圆柱壳的入水空泡随着速度的增加从波动流动转变为云化流动。
朱棒棒、施红辉等[12]曾经研究了刚性圆柱体入水过程中空泡面积、空气携带量以及空泡面闭合时间的变化。温俊生、施红辉等[13]研究了头型对回转体垂直入水时空泡面闭合的影响。这些研究的应用背景主要是射弹或炸弹的入水。在研究用导弹入水攻击潜艇时,必须考虑两端封闭圆柱壳体的入水问题。因此,本文在之前研究的基础上,选择了一组不同头型弹性薄壳圆柱体,利用ANSYS/LS-DYNA有限元软件,采用ALE方法,对入水过程进行了三维流固耦合模拟,主要对比了不同头型弹性圆柱壳的变形、最大压力、入水运动规律,对比了平头刚性圆柱壳与不同头型弹性圆柱壳的的入水运动过程。
1 数值模型
1.1 控制方程
本文假设流体为不可压缩流体,不可压缩牛顿流体的质量和动量方程的ALE形式可以表征为如下形式[14]:
·v=0
(1)
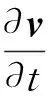
(2)
式中:t为时间;v为流体速度;w为网格速度;f为流体体力项;流体应力张量表示为如下形式:
(3)
式中:I为单位矩阵,p为压力,Re为雷诺数。
1.2 材料模型
圆柱壳模型材料采用线弹性材料,水采用Null材料模型,圆柱壳模型屈服函数数学描述如下:
σ=Eε
(4)
式中:σ为应力分量,E为弹性模量,ε为应变分量。状态方程采用Gruneisen状态方程:
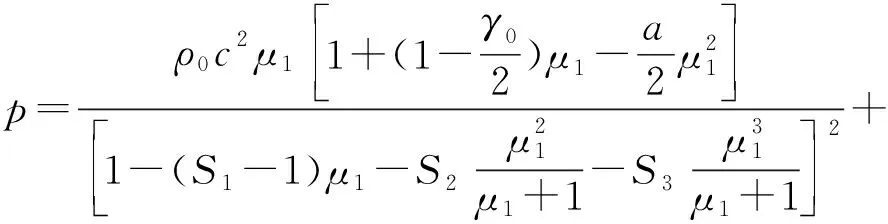
(5)
式中:c为介质声速;S1=1.921,S2=-0.096,S3=0;γ0=0.35,为Gruneisen常数;a为γ0和介质压缩比μ1的一阶体积修正量;U1为单位体积内能。μ1形式如下:
(6)
式中:ρ0为常温状态下水的初始密度,ρ为水的当前密度。
1.3 模型、计算区域及边界条件
模型的二维截面如图1所示。由左至右分别为平头弹性圆柱壳、90°锥角弹性圆柱壳、120°锥角弹性圆柱壳、平头圆柱实体。长度L均为80 mm,壳体厚度δ均为2 mm。材料的弹性模量E=70 GPa,泊松比ν=0.33,密度ρs=2 700 kg/m3。
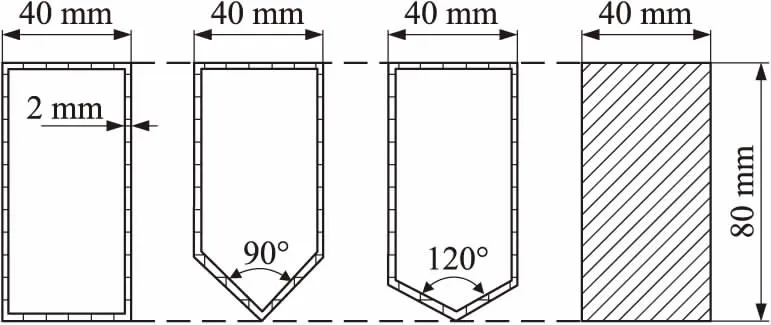
图1 模型示意图
计算区域示意图如图2所示,其中,图2(a)为二维截面示意图,图2(b)为三维正交示意图。为提高计算效率,建模时,在ANSYS/LS-DYNA中采用cm-g-μs单位制。由于本文的计算模型为均质回转体模型,因此本文只建立了四分之一模型进行计算。XOZ与YOZ平面设置为约束边界条件,流场其余边界均设置为无反射边界条件(排除壁面反射波对计算的干扰)。圆柱壳体直径Dn=40 mm,初始位置位于其头部距自由界面10 mm的空气域中。计算区域设置为圆柱域,包括空气域和水域两部分,其中,圆柱域半径为6Dn,空气域长度为5Dn,水域长度为8Dn。圆柱壳的入水初速度为50 m/s
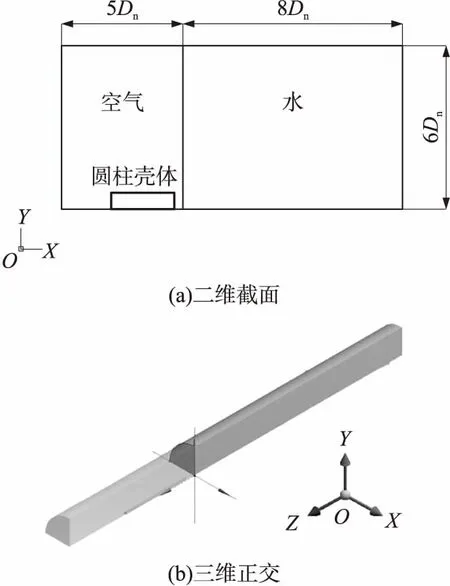
图2 计算区域示意图
1.4 网格划分
本文的计算方法采用ALE方法,选取SOLID 164单元对水、空气及圆柱壳体进行定义,采用Lagrange网格对圆柱壳体进行离散化,采用Euler网格对流体域进行离散化,通过用户自定义关键字在流体和固体之间施加耦合算法。固体与流体的网格最小尺寸均为2 mm。本文只在自由面及圆柱壳附近加密网格,这样可大大提高计算效率。网格单元数如表1所示。
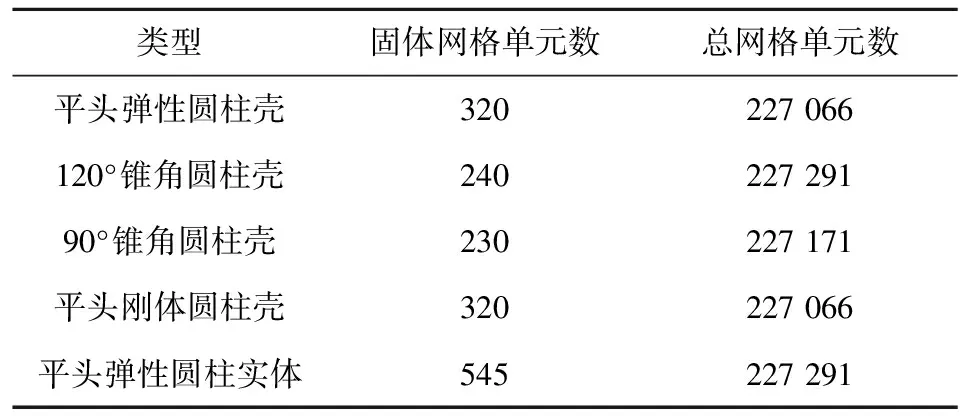
表1 网格单元数
2 数值验证
考虑到实验会存在测量与计算误差,模拟会存在精度问题,导致实验与模拟之间会存在差异,笔者通过对文献[15]中的圆柱壳模型以1.98 m/s的初速度入水过程进行计算来验证本文计算方法的准确性。在圆柱壳下设置了5个压力监测点,监测点上的冲击压力峰值ps对比如图3所示,图中,横坐标为压力检测点到圆心的距离d。数值模拟结果与文献[15]中实验结果的最大误差为8.7%,该误差小于10.0%,本文认为这个范围可以接受,故采用该方法进行数值模拟。
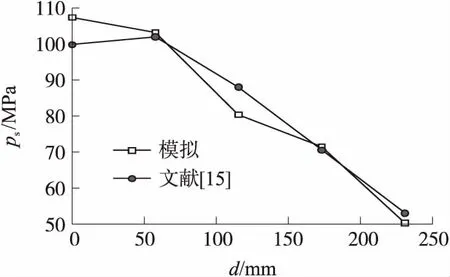
图3 数值模拟结果与文献[15]实验结果的对比
3 计算结果及分析
3.1 不同头型弹性圆柱壳入水过程水相图
不同头型弹性圆柱壳入水过程水相图如图4所示,每幅图之间的时间间隔为1 ms,t=0 ms对应的时间为入水0 ms时刻(即圆柱壳头部刚接触水面时刻),依此类推。从图中可以清晰地观察到,3种不同头型弹性圆柱壳入水超空泡的直径从大到小的顺序为:平头弹性圆柱壳,120°锥角弹性圆柱壳,90°锥角弹性圆柱壳。

图4 不同头型入水过程水相图
3.2 不同头型弹性圆柱壳入水过程中的变形情况
当弹性圆柱壳从空气中进入水中时,其下表面与上表面均会发生一定程度的变形。不同头型弹性圆柱壳入水过程中壳体的变形情况如图5所示。
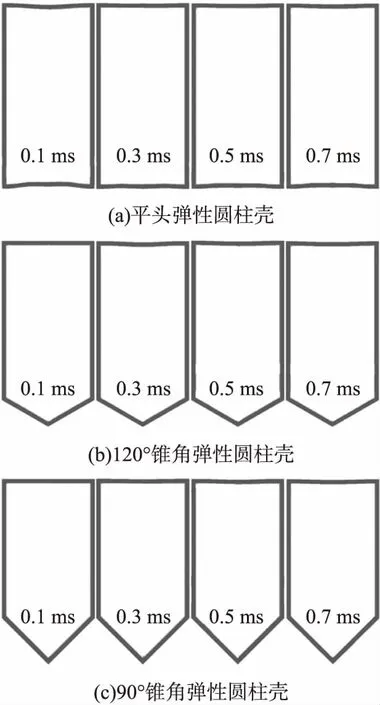
图5 不同头型弹性圆柱壳变形情况
图5中每幅图之间的时间间隔为0.2 ms,t=0.1 ms对应的时间为入水0.1 ms时刻,依此类推。对比发现,平头弹性圆柱壳上、下表面均发生明显变形,而锥角弹性圆柱壳(120°与90°锥角)只有上表面变形显著。
为了更加直观地呈现不同头型圆柱壳的变形情况,本文从3种不同头型的弹性圆柱壳的圆心位置出发,先是对比了平头弹性圆柱壳上、下表面的变形,然后进一步对比了3种不同头型弹性圆柱壳上表面的变形情况。
图6对比了平头弹性圆柱壳上、下表面变形ld。ld>0,表示变形与运动方向相反;ld<0,表示变形与运动方向相同。下表面的变形存在3个波峰,波峰出现的时间依次为入水0.1 ms时刻、入水0.6 ms时刻、入水1.1 ms时刻。上表面的变形存在2个波峰,波峰出现的时间依次为入水0.1 ms时刻、入水0.7 ms时刻。下表面的振动频率约为2 000 Hz,上表面的振动频率约为1 667 Hz。平头弹性圆柱壳下表面变形大于上表面,上、下表面均表现为凹陷状态。

图6 平头弹性圆柱壳上、下表面中心点变形对比
图7对比了不同头型弹性圆柱壳上表面的变形ld。依然规定:ld>0,表示变形与运动方向相反;ld<0,表示变形与运动方向相同。120°锥角和90°锥角弹性圆柱壳上表面的变形与平头弹性圆柱壳上表面的变形有所不同,它们的变形只存在一个波峰。观察到平头弹性圆柱壳上表面的变形程度最大,120°锥角弹性圆柱壳上表面的变形次之,而90°锥角弹性圆柱壳体上表面的变形最小。平头弹性圆柱壳第1个波峰出现的时间最早,为入水0.1 ms时刻(第2个波峰为0.7 ms时刻);120°锥角弹性圆柱壳波峰出现时间次之,为入水0.3 ms时刻;波峰出现最晚的是90°锥角弹性圆柱壳,其在入水0.5 ms时刻出现波峰。平头、120°锥角、90°锥角这3种头型弹性圆柱壳上表面的变形均处于向内凹陷的状态,并随时间逐渐趋于一致。
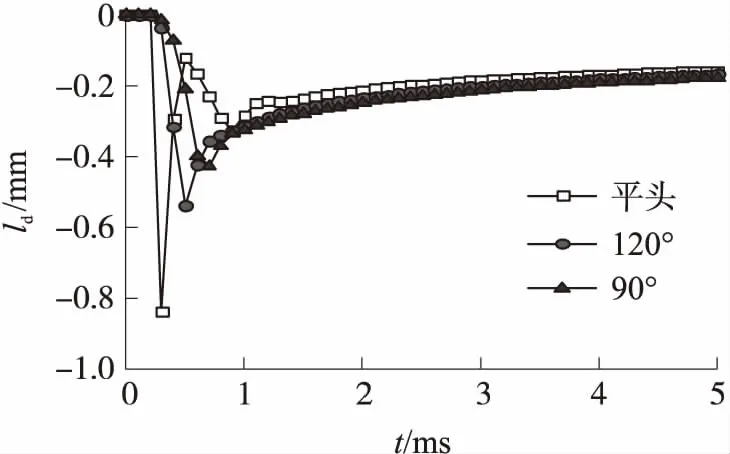
图7 不同头型弹性圆柱壳上表面中心点的变形对比
3.3 平头圆柱壳入水过程的压力变化
为了研究弹性圆柱壳产生变形的原因,本文在圆柱壳下表面沿径向方向设置了5个压力监测点分别为r1=40 mm,r2=8 mm,r3=12 mm,r4=16 mm,r5=50 mm,如图8所示。
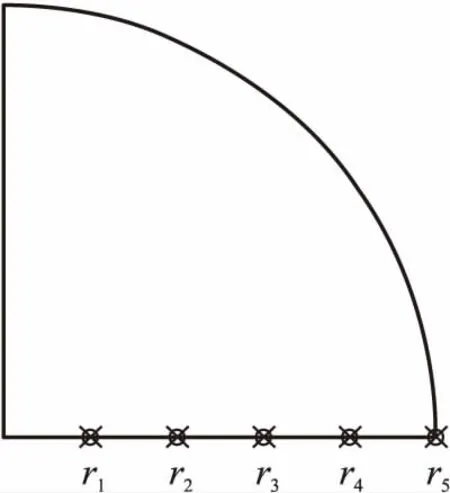
图8 压力检测点示意图
图9(a)、9(b)分别为平头弹性圆柱壳下表面和平头弹性圆柱实体下表面在每个压力监测点下的压力(ps)变化图。
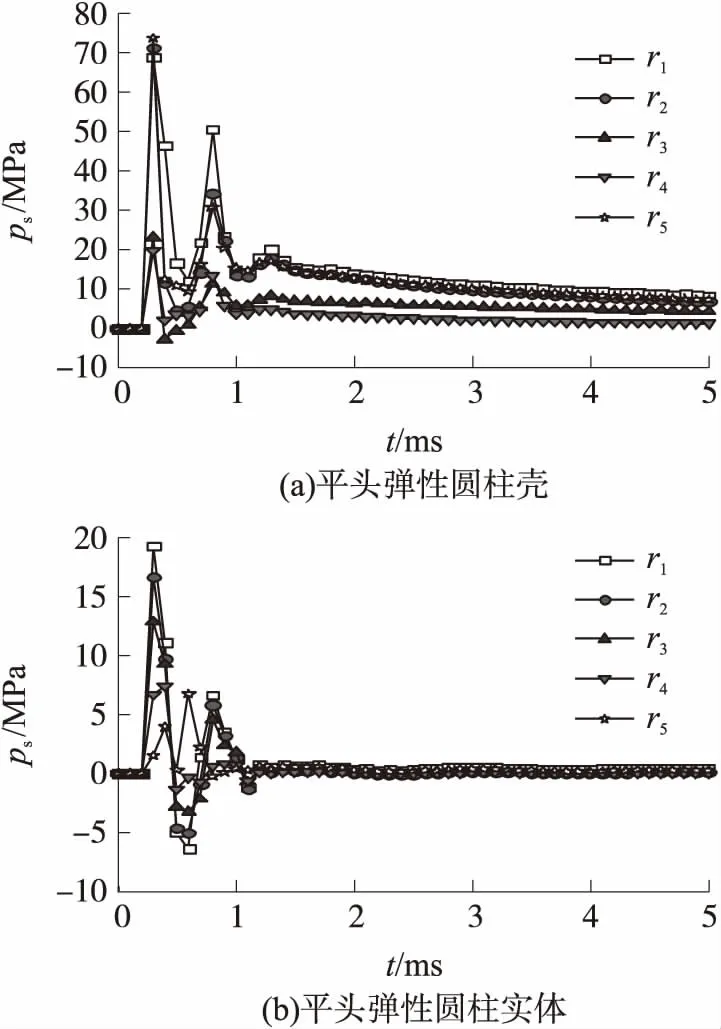
图9 压力变化图
图9(a)与图6变形图中波峰出现的时间一致,且均有3个波峰。对比图9(a)与图9(b)发现,壳体下表面受到的压力大概是实体的3.5倍。可以理解,在流体冲击力的作用下,物体高速入水时实体下发生的变形要小于壳体,因此实体受到的压力小于壳体受到的压力。由图9可以观察到,实体压力变化曲线只存在2个波峰,与壳体前2个波峰出现的时间相同。不同头型弹性圆柱壳最大峰值压力pmax的对比情况见表2。圆柱壳头部受到的最大压力随着锥角的增大而增大(平头圆柱壳等效为180°锥角),这说明压力受几何形状与弹性形变的变形影响较大,这与文献[15]中的结论是一致的。

表2 不同头型弹性圆柱壳最大压力变化
3.4 不同头型圆柱壳的入水运动规律
不同头型圆柱壳入水过程中加速度as的对比如图10所示。圆柱壳撞击水面时,会瞬间产生巨大的流体冲击力,其加速度会迅速上升。随后,圆柱壳的动能传递给液面,克服表面张力使液面产生变形,圆柱壳周围的空气随着液体向圆柱壳头部周围流动被携带进入水中,液体发生汽化,在空气和水蒸气的共同作用下,圆柱壳的周围形成空泡,所以圆柱壳的加速度又会减小。最后,不同头型弹性圆柱壳的加速度趋向于一个相同的值。平头弹性圆柱壳加速度在入水0.1 ms时刻达到峰值,而且峰值最大;其次是平头刚体圆柱壳,略小于平头弹性圆柱壳;120°锥角弹性圆柱壳在入水0.2 ms时刻加速度达到峰值,该峰值约为平头弹性圆柱壳加速度峰值的一半;90°锥角弹性圆柱壳在入水0.3 ms时刻加速度达到峰值,其峰值最小。
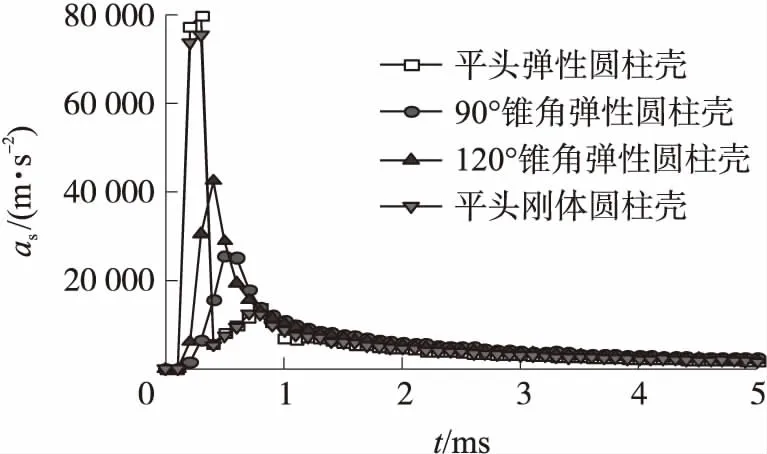
图10 不同头型圆柱壳入水加速度对比
入水过程中速度vs的对比如图11所示。由图可见,速度变化规律与加速度的变化规律一致。不同头型圆柱壳入水后速度vs从大到小的顺序为:90°锥角弹性圆柱壳,120°锥角弹性圆柱壳,平头刚体圆柱壳,平头弹性圆柱壳。在入水初期,速度均下降明显,下降趋势随时间逐渐变缓。
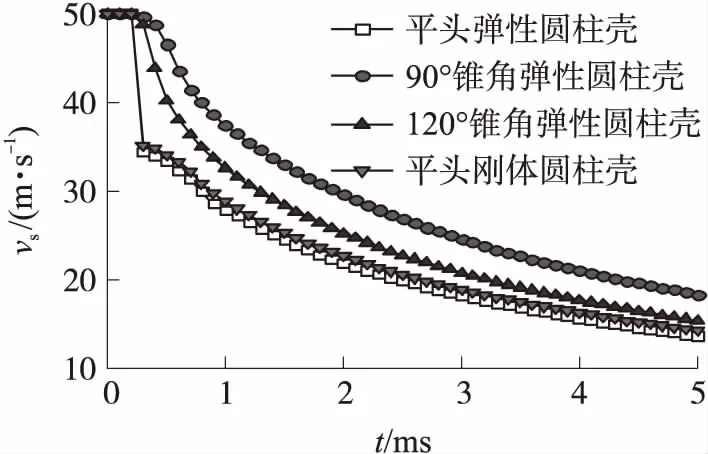
图11 不同头型圆柱壳入水速度对比
在3.3节中,本文发现,压力是造成圆柱壳下表面变形的主要原因。本文进一步分析发现,由于物体穿过介质界面时速度迅速衰减,所以其上表面的变形主要是由惯性作用造成的。
4 结论
通过对不同头型弹性圆柱壳入水过程的数值模拟并与文献中的结果进行对比,本文得到了如下结论:
①圆柱壳上表面在惯性作用下发生变形,下表面在流体冲击力作用下发生变形。圆柱壳的上、下表面均处于凹陷状态。
②平头圆柱壳上表面变形曲线存在2个波峰,其振动频率约为1 667 Hz;下表面变形曲线存在3个波峰,其振动频率为2 000 Hz。锥角越大,最大变形出现的时间越早,上表面的变形越大。
③平头弹性圆柱壳变形波峰和压力波峰出现的时间相一致。平头圆柱壳下表面压力曲线存在3个波峰,平头圆柱实体下表面压力曲线存在2个波峰,两者下表面受到的最大压力均随其头部锥角的增大而增大。
④锥角越大,圆柱壳体的加速度越大,加速度峰值出现的时间越早。刚性圆柱壳入水后的速度略大于弹性圆柱壳。本文的计算结果表明,圆柱壳的锥角越小,入水时受到的冲击压力越小,入水后物体的速度衰减越慢,这也符合一般的常识。
