固体火箭高温高压复杂燃气系统的黏性系数和导热系数计算

陈 军

(南京理工大学 机械工程学院,江苏 南京 210094)

目前,对输运性质黏性系数和导热系数的计算方法仍然主要集中于低压纯组分或双组分,许多学者提出了很多理论模型[1-6]。但关于高压条件下的输运特性,尤其是高压混合物的研究很少,还缺乏充足的数据支持目前很少的研究结论。而火箭燃气的特征正是高温高压混合物,燃气组分主要为无机物,其中极性组分占比很大[7-9]。因此,火箭燃气输运系数的计算与验证非常困难[10]。本文试图从大量的成熟研究结论中,寻找出尽可能满足火箭燃气特征的最合理的计算方法。由于缺乏高温高压混合燃气的实验数据,本文主要以单组分和双组分以及少量多组分的数据进行验证。

1 高温高压下复杂燃气系统黏性系数和导热系数计算的理论模型

考虑分子弹性模型,目前计算黏性系数μ和导热系数κ时广泛采用了利用伦纳德-琼斯(Lennard-Jones)势修正得到的恩斯克-查普曼(Enskog-Chapman,E-C)公式,即

(1)

(2)

式中:Ωμ,Ωκ为伦纳德-琼斯参数,称为碰撞积分;M,T分别为摩尔质量(kg/kmol)和温度(K);σ为碰撞直径(10-10m)。按上述单位计算,μ,κ的单位分别为Pa·s和W/(m·K)。伦纳德-琼斯参数Ωμ,Ωκ与特性对比温度T*=T/(ε/k)有关,ε/k为弹性分子的特征参数,具有温度的量纲;ε为分子势,k为玻尔兹曼常数。

E-C公式一般只适用于低压条件下单原子分子组分。对于高温高压下复杂燃气系统,需要进行修正,主要考虑如下因素:多原子分子,极性与非极性,混合物,高压。

①低压非极性多原子纯组分。

E-C公式也直接适用于低压非极性多原子纯组分黏性系数,但一般不适于导热系数和扩散系数计算。导热系数可在E-C公式基础上进行修正,著名的是欧肯修正方法,但该修正量偏低,本文采用较为适中的斯蒂尔-桑多斯(Stiel-Thodos)修正,即

(3)

②低压极性多原子纯组分。

对于极性组分的黏性系数,本文选用CHUNG方法,即对E-C式(1)引入修正系数φ,得:

(4)

修正系数为

(5)

式中:ω为极性组分的偏心因子,μpr为约化偶极矩,k1为强极性分子的修正因子。

对于极性组分的导热系数,本文同样选用CHUNG修正方法,即

(6)

式中:ψ为修正系数,见文献[1]。

③低压混合物。

多组分混合物,先单独计算纯组分的输运系数,然后按照一定方法合成。对于黏性系数,本文均采用里切恩贝格方法合成,即

(7)

式中:i,j,l表示任意组分的序号,包括N种组分;K,H为组合变量,见文献[1]。

导热系数采用简化的威尔克修正,即

(8)

式中:x为摩尔分数;

(9)

④高压修正。

气体黏性系数和导热系数只有在压强大于2.5 MPa下才有明显影响,本文均选用CHUNG法对它们进行修正计算。该方法以低压CHUNG法为基础(故适用于极性组分,但对非极性组分的导热系数同样适用),高压修正公式分别为

(10)

(11)

式中:TC为组分的临界温度(K);VC为组分的临界体积(cm3/mol);μ*,G2,E6,E7,q为中间变量,见文献[1];μ0为低压下的黏性系数;Tr=T/TC,为对比温度;y=VC/(6Vm);Vm为实际气体的摩尔体积(cm3/mol)。

在高压下,实际气体并不满足理想气体状态方程,因此,实际气体的摩尔体积Vm需要通过求解压缩因子来计算得到。本文采用李-凯斯勒(Lee-Kesler)模型求解压缩因子Z,即

(12)

式中:Z0,ZR分别为简单流体和参考流体的压缩因子。得到压缩因子Z后,实际气体的摩尔体积Vm为

(13)

对于非极性分子组分的黏性系数,采用里切恩贝格修正,即

(14)

式中:系数Q,A,B,C,D定义见文献[1];pr=p/pC,pC为组分的临界压强。

⑤高压混合物。

总体上,与低压混合物类似,高压混合物的输运系数可以由前述高压纯组分的输运系数通过一定规律合成而得到,也可以对低压混合物通过高压修正得到,但前者是主要的方法。本文选用与低压混合物合成相同的里切恩贝格方法。

由于导热系数的计算误差较大,本文还采用了高压CHUNG混合方法,即利用纯组分的高压CHUNG修正式(11),其中参数按照一定规律混合,即

(15)

式中:下标m表示混合物;系数B6,B7以及参数混合规则见文献[1]。

计算出黏性系数μ和导热系数κ后,输运相似准则数普朗特数Pr即可计算如下:

(16)

式中:cp为比定压热容。

计算纯组分的相似数后,混合物的相似数可按各个组分的普朗特数混合即可:

(17)

上述黏性系数和导热系数的计算模型汇总于图1和图2中。

图1 黏性系数计算模型

图2 导热系数计算模型

2 计算模型的验证

高温高压气体及其混合物的实验非常困难,缺乏足够的实验数据,特别是缺乏高温高压多组分混合物的实验数据,因此,不能够全面检验计算模型的正确性。为此,本文主要检验组成火箭高温高压复杂燃气的双组分或三组分混合物的计算结果。

不考虑金属添加物,火箭燃气的主要组分包括:CO2,CO,H2O,H2,N2,HCl,SO2,NO等[9-10],都是多原子组分,其中非极性组分为CO2,H2,N2等,极性组分为CO,H2O,HCl,SO2,NO等。组分H2O,HCl,SO2为强极性组分,组分H2为轻质组分,这些组分在混合物输运性质的理论模型中都是很难准确计算的。

上述模型对于低压纯组分的验证已经十分充分[1-17],这里只给出混合物在高温高压下的验证。

①黏性系数的计算检验。一些与火箭燃气相关的混合物的黏性系数计算与实验数据比较列于表1和表2中。表中,η为相对误差,x为组分的摩尔分数。

表1 低压混合物在不同温度或不同混合占比(摩尔分数)下的黏性系数

表2 高压混合物黏性系数

上述数据表明,黏性系数的计算模型在高温和高压下均具有较好的计算精度。但缺乏同时具有高温和高压特征的实验数据。

②导热系数的计算检验。一些与火箭燃气相关的混合物的导热系数计算与实验数据比较列于表3和表4中。

表3 低压混合物在不同温度或不同混合比(摩尔分数)下的导热系数

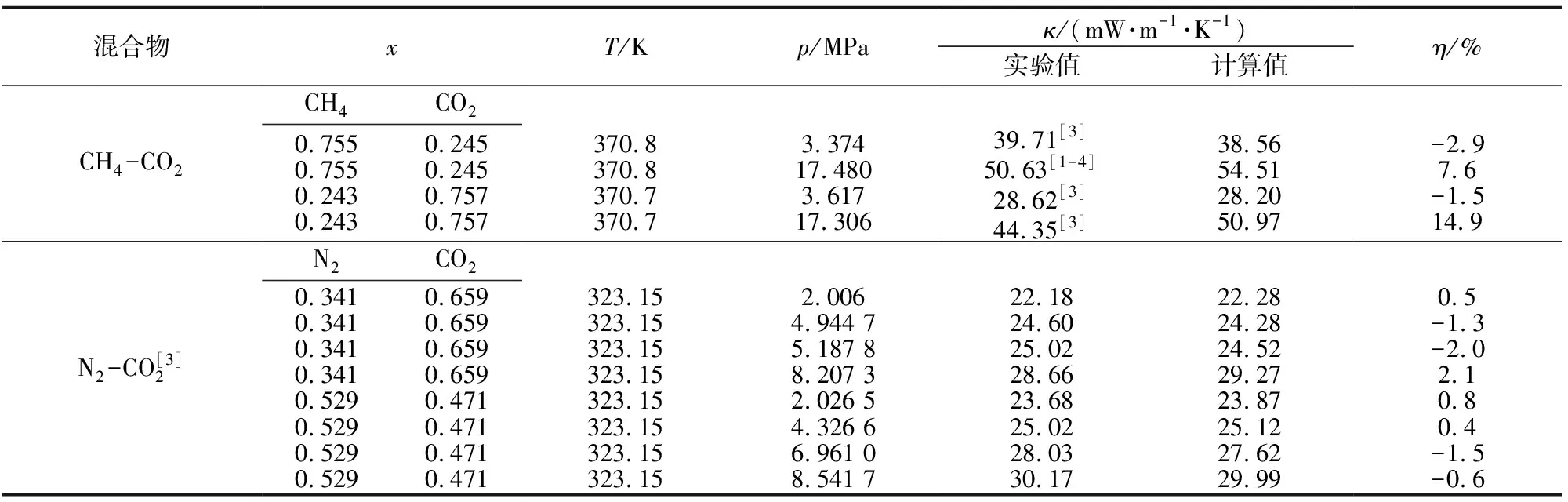
表4 高压混合物在不同温度或不同混合比(摩尔分数)下的导热系数

上述数据表明,导热系数的计算模型在高压下均具有较好的计算精度,但在高温下含H2O混合物(如烟气)的计算误差较大。同样缺乏具有高温和高压特征的实验数据。

3 火箭高温高压复杂燃气的输运系数

这里主要给出不考虑金属添加物的固体推进剂的燃气特征,主要包括双基推进剂(DB)、改性双基推进剂(CMDB)和复合推进剂(CP)。温度和压强按火箭发动机的典型工作范围取值。

3.1 火箭DB推进剂燃气的输运系数

双基推进剂工作的温度取1 500～2 500 K,工作压强取8.0～20.0 MPa,典型燃气组分:CO,CO2,H2,H2O,N2,其中x(CO)=0.47,x(CO2)=0.07,x(H2)=0.2,x(H2O)=0.15,x(N2)=0.11。

在典型工作压强p=10.0 MPa下,不同温度(1 500～2 500 K)时双基推进剂燃气的黏性系数、导热系数和普朗特数如表5所示。

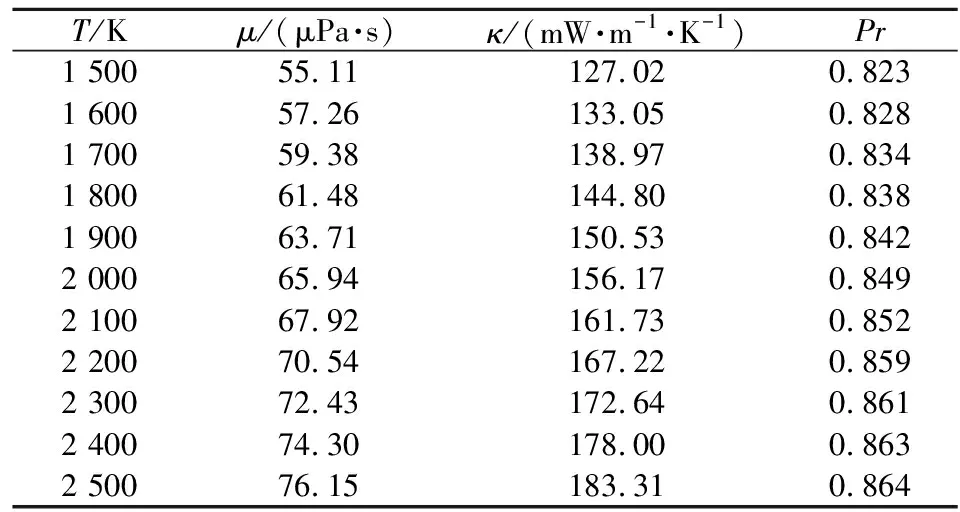
表5 火箭DB推进剂燃气的输运系数(p=10.0 MPa)

在典型温度T=2 200 K下,不同工作压强(8.0～20.0 MPa)时双基推进剂燃气的黏性系数、导热系数和普朗特数如表6所示。

表6 火箭DB推进剂燃气的输运系数(T=2 200 K)

3.2 火箭CMDB推进剂燃气的输运系数

改性双基推进剂工作的温度取2 600～3 800 K,工作压强取8.0～20.0 MPa,典型燃气组分为:HCl,CO,CO2,H2,H2O,N2,x(HCl)=0.1,x(CO)=0.21,x(CO2)=0.2,x(H2)=0.05,x(H2O)=0.32,x(N2)=0.12。

在典型工作压强p=10.0 MPa下,不同温度(2 600～3 800 K)时改性双基推进剂燃气的黏性系数、导热系数和普朗特数如表7所示。

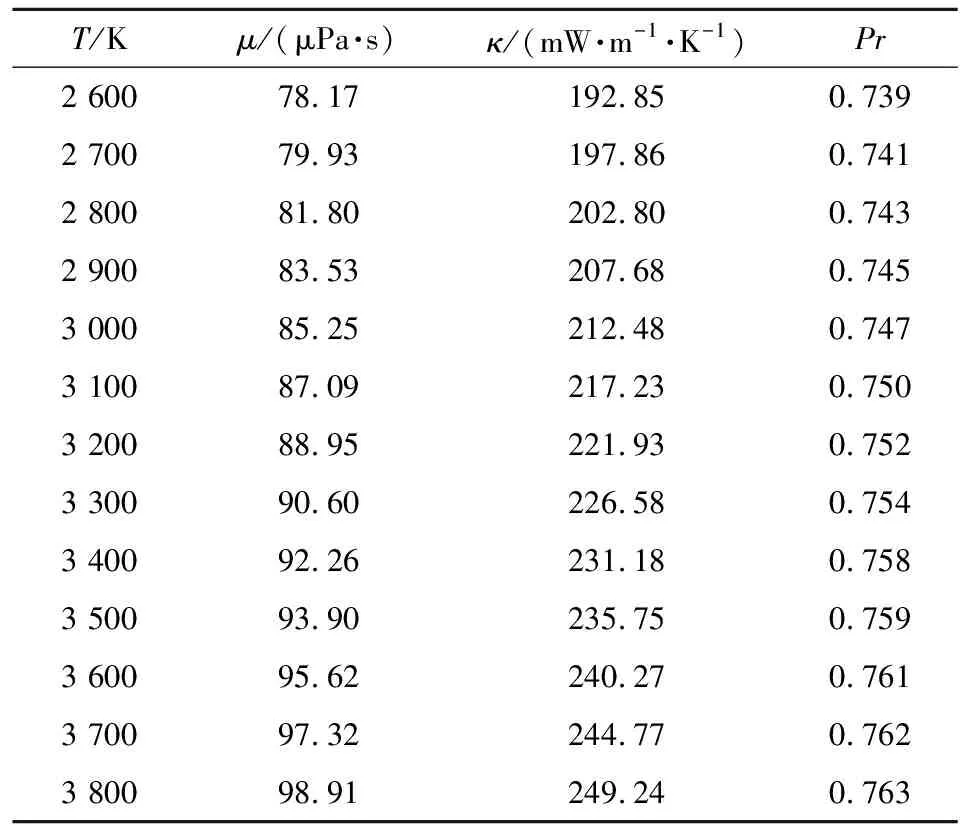
表7 p=10.0 MPa,火箭CMDB推进剂燃气的输运系数

在典型温度T=3 000 K下,不同工作压强(8.0～20.0 MPa)时改性双基推进剂燃气的黏性系数、导热系数和普朗特数如表8所示。

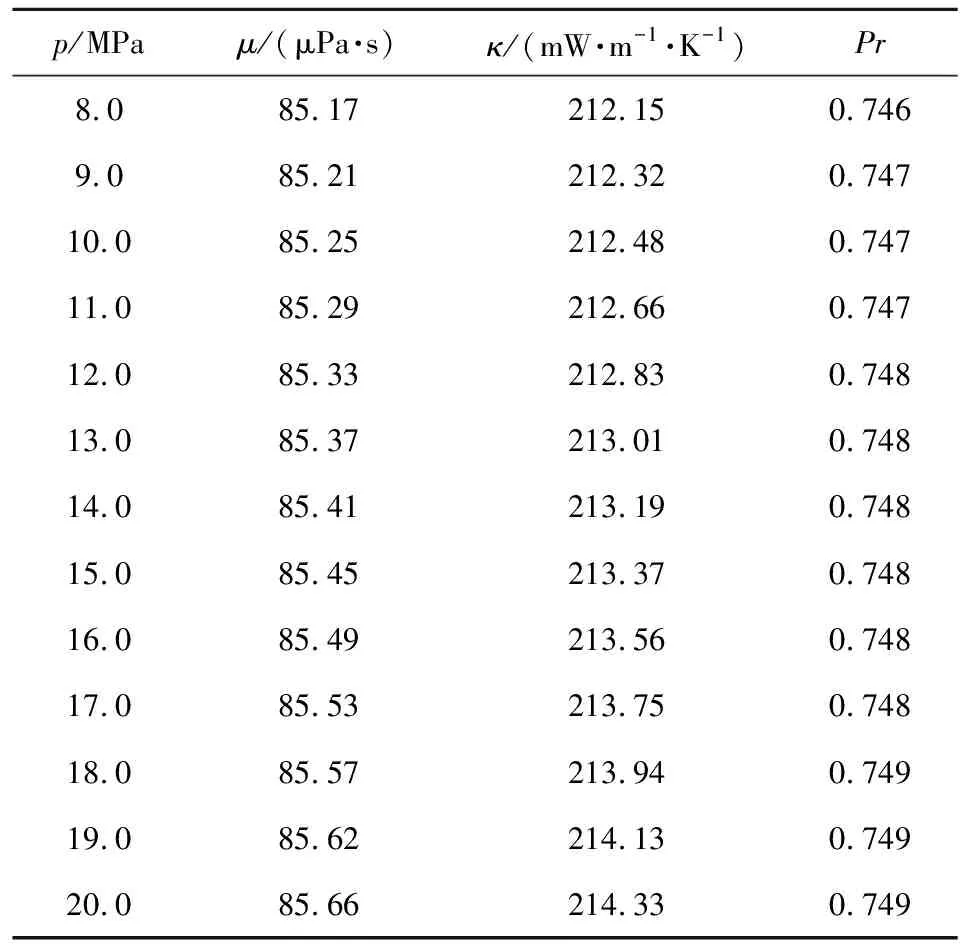
表8 T=3 000 K,火箭CMDB推进剂燃气的输运系数

3.3 火箭AP复合推进剂燃气的输运系数

复合推进剂工作的温度取2 600～3 800 K,工作压强取8.0～20.0 MPa,典型燃气组分为:HCl,CO,CO2,H2,H2O,N2,x(HCl)=0.13,x(CO)=0.25,x(CO2)=0.03,x(H2)=0.2,x(H2O)=0.24,x(N2)=0.15。

在典型工作压强p=10.0 MPa下,不同温度(2 600～3 800 K)时复合推进剂燃气的黏性系数、导热系数和普朗特数如表9所示。

表9 p=10.0 MPa,火箭AP复合推进剂燃气的输运系数

在典型温度T=3 200 K下,不同工作压强(8.0～20.0 MPa)时复合推进剂燃气的黏性系数、导热系数和普朗特数如表10所示。

表10 T=3 200 K,火箭AP复合推进剂燃气的输运系数

4 火箭高温高压复杂燃气输运系数的分析

为便于观察火箭燃气输运系数的变化规律,表5～表10的数据用曲线图3～图8所示。

火箭燃气黏性系数随温度和压强的变化分别如图3、图4所示,可以发现,黏性系数随温度的升高而升高,这与一般气体黏性系数的变化规律一致。

图3 火箭燃气黏性系数随温度的变化

图4 火箭燃气黏性系数随压强的变化

从图3还可以看出,不同推进剂(双基推进剂、改性双基推进剂、复合推进剂)燃气的黏性系数随温度的变化规律非常接近,特别是双基推进剂和改性双基推进剂。图4表明,火箭燃气黏性系数随压强变化很小,一般可以忽略,即可以不考虑压强的影响。

通过最小二乘拟合,得双基推进剂和改性双基推进剂燃气黏性系数随温度的变化函数为

(18)

式中:T0=1 500 K,μ0=55.11 μPa·s。拟合最大相对误差为-0.1%,如图5所示。

图5 双基推进剂和改性双基推进剂燃气无量纲黏性系数随温度的变化

类似地,可得复合推进剂燃气黏性系数随温度的拟合函数为

(19)

式中:T0=2 600 K,μ0=80.35 μPa·s。拟合最大相对误差为0.03%,如图6所示。

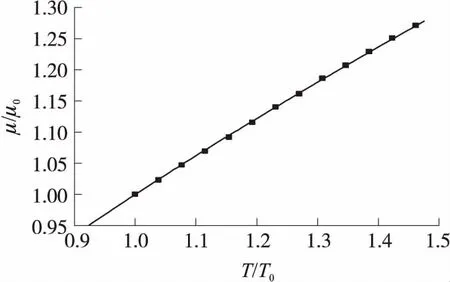
图6 复合推进剂燃气无量纲黏性系数随温度的变化

火箭燃气导热系数随温度和压强的变化分别如图7、图8所示。

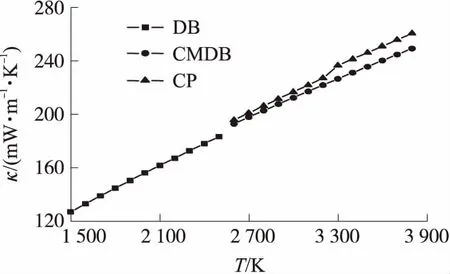
图7 火箭燃气导热系数随温度的变化

图8 火箭燃气导热系数随压强的变化

由图7可以发现,导热系数随温度的升高而升高,这与一般气体导热系数的变化规律一致。图8表明,火箭燃气导热系数随压强变化很小,一般可以忽略,即可以不考虑压强的影响。

从图7还可以发现,双基推进剂和改性双基推进剂燃气的导热系数随温度的变化规律非常接近。通过最小二乘拟合,可得双基推进剂和改性双基推进剂燃气导热系数随温度的变化函数为

(20)

式中:T0=1 500 K,κ0=127.02 mW/(m·K)。拟合最大相对误差为-0.1%,如图9所示。

图9 双基推进剂和改性双基推进剂燃气无量纲导热系数随温度的变化

类似地,可得复合推进剂燃气导热系数随温度的拟合函数为

(21)

式中:T0=2 600 K,κ0=195.65 mW/(m·K)。拟合最大相对误差为0.05%,如图10所示。

火箭燃气普朗特数的变化如图11和图12所示。可以发现,普朗特数随温度呈现微弱变化,随压强变化很小。双基推进剂燃气普朗特数随温度的最大变化为4.98%,改性双基推进剂为3.25%,复合推进剂为1.81%。

因此,普朗特数可以近似处理为常数,按平均处理,可得双基推进剂燃气的普朗特数为0.85,改性双基推进剂燃气的普朗特数为0.75,复合推进剂燃气的普朗特数为0.89。

图10 复合推进剂燃气无量纲导热系数随温度的变化

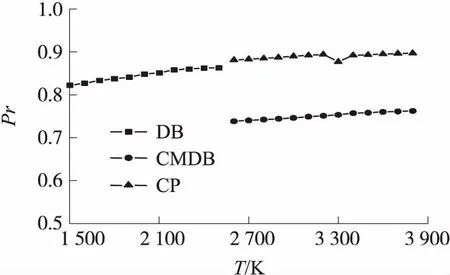
图11 火箭燃气普朗特数随温度的变化

图12 火箭燃气普朗特数随压强的变化

5 结论

通过对3种主要不含金属添加物的固体推进剂(双基推进剂、改性双基推进剂和复合推进剂)燃气的黏性系数和导热系数的计算与分析,得出如下结论:

①双基推进剂和改性双基推进剂燃气黏性系数随温度变化的幂指数为0.630 4(适于温度1 500～3 800 K,T0=1 500 K,μ0=55.11 μPa·s),复合推进剂为0.631 7(适于温度2 600～3 800 K,T0=2 600 K,μ0=80.35 μPa·s)。

②双基推进剂和改性双基推进剂燃气导热系数随温度变化的幂指数为0.732 8,适于温度1 500～3 800 K,T0=1 500 K,κ0=127.02 mW/(m·K);复合推进剂燃气导热系数随温度变化的幂指数为0.760 6,适于温度2 600～3 800 K,T0=2 600 K,κ0=195.65 mW/(m·K)。

③在压强为8.0～20.0 MPa范围内,火箭燃气的黏性系数和导热系数随压强的变化很小,可不考虑压强的影响。

④火箭燃气的普朗特数随温度呈现微弱变化,随压强变化很小,可按平均近似处理为常数。双基推进剂燃气的普朗特数为0.85,改性双基推进剂燃气的普朗特数为0.75,复合推进剂燃气的普朗特数为0.89。双基推进剂和复合推进剂燃气的普朗特数与传统的经验取值0.72[9]左右存在较大差别,但改性双基推进剂的普朗特数与经验值0.72比较接近。

上述分析与结论给出了火箭高温高压复杂燃气黏性系数和导热系数的估算方法与取值范围,由于很难从实验上进行验证,故只有在以后不断的理论实践中分析其合理性并不断改进。同时,本文没有考虑凝聚相对输运性质的作用,这有待进一步深入研究。